基于元件组合理论的砂岩动态损伤本构模型*

江雅勤，吴帅峰，刘殿书，贾 贝，王 蒙，李晓璐

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083； 2.中国水利水电科学研究院岩土工程研究所，北京 100044)

在地下矿开采、大断面公路隧道、大型地下工程、高陡岩石边坡、深埋洞室等岩体工程中，常常遇到砂岩动力学问题。致密砂岩气是国际上开发规模最大的非常规天然气。中国致密砂岩气的储量丰富，具有广阔的发展前景，在天然气能源结构中的重要性日趋显著[1-2]。砂岩在钻井开采时承受着冲击荷载，要提高机械钻井速度和开发水平、降低开发成本，对砂岩的动态力学特性进行研究是十分必要的[3]。牛雷雷等[4]利用摆锤冲击加载分离式霍普金森压杆(split Hopkinson pressure bar， SHPB)装置，得出动态抗压强度与加载应变率具有正相关性的结论。朱晶晶[5]对砂岩进行冲击试验，结果表明在动态应力峰值附近，砂岩损伤发生变化，岩石内部裂纹进入发育阶段。石祥超等[6]基于三轴动态试验，给出了砂岩的Johnson-Holmquist模型参数，并借助AUTODYN软件模拟验证了参数的准确性。赵光明等[7]对砂岩和泥岩两种典型的软岩进行冲击试验，通过用损伤体代替非线性弹簧，修改了朱-王-唐模型，建立了用于软岩的动态本构模型。到目前为止，还未见能够全面反映砂岩动态力学特性的本构关系[8]，因此构建砂岩的动态本构模型具有重要的实际意义。

本研究中利用SHPB对砂岩进行冲击压缩试验，根据试验结果，考虑应变率效应和损伤软化效应，结合元件组合理论，构建基于损伤的砂岩本构模型，并利用LS-DYNA软件二次开发平台对致密砂岩的损伤本构模型进行模拟验证。

1 动态力学性能实验研究

从图2和图3可以看出，砂岩在冲击作用下具有如下特征。

(1) 弹塑性特征。在不同的中低应变率作用下，砂岩的本构曲线在达到峰值应力之前具有不同的特性。当应变率小于50 s-1时，砂岩的本构曲线在达到峰值应力前基本呈近似线弹性，部分试件表面有裂纹，但均未发生破碎。当应变率大于50 s-1时(见图3)，达到峰值应力前的应力-应变曲线可分为3个阶段。第1阶段(AB段)为近似线弹性段。第2阶段(BC段)中，应力-应变曲线的斜率较小，应变增量较大，而应力增长缓慢，表明砂岩进入塑性阶段。在应力波作用下砂岩内部原始裂隙扩展，形成大量新裂隙，但还未形成宏观上的破坏。第3阶段(CD段)是塑性增强阶段，斜率明显增大，但远小于AB段斜率，应力增加较快，逐渐达到应力峰值。当塑性应变较小时，试件裂纹继续发育，内部发生损伤，但未发生明显的宏观破坏；当应变达到某临界值时，试件发生破坏。达到峰值应力后(DE段)，应变持续缓慢增加，而应力迅速下降，曲线为正卸载，未出现回弹现象，表明砂岩发生不可逆的变形损伤和破坏。

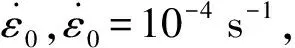
式中：KD为损伤待定系数，β为材料常数。

(3) 黏性特征。砂岩的动态强度与应变率具有明显的相关性，即动态强度随着应变率的增大而增大。这种特征在本构模型中描述为黏性，在元件理论中用牛顿体表示：

式中：σ为应力，η为黏滞系数。

2 冲击作用下砂岩动态本构模型构建

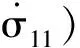
对于三参量模型，根据串、并联元件基本规则，可得：

其中：

由此可得：

因此式(6)可化为：

其中：

采用拉普拉斯变换消去函数中的应力率项，使本构方程变为应变和应变率的函数。对式(11)进行拉普拉斯变换[11]，可得：

式中：s为复变参量。把边界条件σ2(0)=0代入式(13)，得到：

对式(14)进行拉普拉斯逆变换，可得：

将式(16)化简整理得：

根据应变率定义，式(17)可化为：

对于Maxwell模型，由串联得:

其中:

则

对式(21)进行拉普拉斯变换，得：

把式(19)代入式(22)，结合边界条件ε1(0)=0时，σ1(0)=0，式(22)变换为:

再由拉普拉斯逆变换，求得:

根据图4构建的含损伤的砂岩本构模型为:

式中：E1、E2、E3、E4为拟合参数。

3 SHPB冲击砂岩模拟应用

LS-DYNA是常用的显式非线性动力分析程序，以Lagrange算法为主，能够计算碰撞、爆炸、冲击等问题。运用LS-DYNA进行SHPB系统的模拟计算时，采用Lagrange中心差分算法，通过用户材料子程序UMAT[12]定义模型，通过定义失效关键字*MAT_ADD_EROSION实现单元失效[13]。自定义本构模型在LS-DYNA中的计算流程如图5所示，按上述方法编译程序，使用新生成的求解器提交K文件至求解器中求解。

按照试验设备建立直径为50 mm的SHPB系统模型，其中撞击杆、入射杆和透射杆长度分别为400、2 000和2 000 mm，试件长度为50 mm。系统杆密度为2 800 kg/m3，弹性模量为77 GPa，泊松比为0.27。对7.5、9.5、11.5和13.5 m/s 4种不同冲击速度(v)下的SHPB试验进行模拟，与对应的试验情况进行比较分析。

图6为4种冲击速度下砂岩试验和数值模拟得到的应力-应变曲线。从图6中可以看出：对于弹性极限及其对应的应变，试验曲线和模拟曲线具有较好的一致性；模拟曲线能够较好地描述弹性段结束时短暂的塑性段；在塑性段结束后，模拟曲线同样能准确地描述塑性强化段，具有与试验曲线较一致的峰值强度，所对应的峰值应变较试验曲线略小，而最大应变基本一致。模拟结果显示出与试验结果相同的应变率效应，砂岩的动态强度随着冲击速度的提高而提高。说明本研究中所构建的动态本构方程可以较全面地反映砂岩的动态本构关系，具有较好的模拟效果。

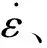
方法v/(m·s-1)ε/s-1σd,max/MPaεmax/10-3方法v/(m·s-1)ε/s-1σd,max/MPaεmax/10-3模拟7.555.5348.081.820试验7.552.3950.932.000模拟9.564.0663.182.170试验9.564.7163.322.260模拟11.581.3688.943.920试验11.578.2395.873.900模拟13.585.2597.146.080试验13.590.69102.746.017

4 结 论

(1) 对砂岩进行了动态冲击试验，由砂岩的动态本构曲线可知：砂岩具有动态强度随应变率增大而增强的黏性特征，同时具有近似线弹性特征、理想塑性及塑性增强特征；损伤的发展与应变率相关，并由此建立了损伤与应变率及应变的函数关系。

(2) 根据砂岩的动态力学特征，采用元件组合理论，构建了由损伤体、Maxwell模型和三参量模型组合而成的含损伤的砂岩本构模型。

(3) 利用LS-DYNA对所构建的本构模型进行内嵌编译，并对砂岩进行冲击试验模拟。结果显示，模型所得的应力-应变曲线弹性段、动态峰值强度及最大应变均与试验情况一致，且相对误差小于10%，表明该模型可以较全面、准确地反映砂岩的动态本构关系。

参考文献:

[1] 魏国齐,张福东,李君,等.中国致密砂岩气成藏理论进展[J].天然气地球科学,2016,27(2):199-210.

WEI Guoqi, ZHANG Fudong, LI Jun, et al. New progress of tight sand gas accumulation theory and favorable exploration zones in China[J]. Natural Gas Geoscience, 2016,27(2):199-210.

[2] 郭迎春,庞雄奇,陈冬霞,等.致密砂岩气成藏研究进展及值得关注的几个问题[J].石油与天然气地质,2013,34(6):717-724.

GUO Yingchun, PANG Xiongqi, CHEN Dongxia, et al. Progress of research on hydrocarbon accumulation of tight sand gas and several issues for concerns[J]. Oil & Gas Geology, 2013,34(6):717-724.

[3] 蔡灿,伍开松,袁晓红,等.中低应变率下的岩石损伤本构模型研究[J].岩土力学,2015,36(3):795-803.

CAI Can, WU Kaisong, YUAN Xiaohong, et al. Damage constitutive model of rock under medium and low strain rates[J]. Rock and Soil Mechanics, 2015,36(3):795-803.

[4] 牛雷雷,朱万成,李少华,等.摆锤冲击加载下砂岩中应变率动力特性的试验研究[J].岩石力学与工程学报,2014,33(12):2443-2450.

NIU Leilei, ZHU Wancheng, LI Shaohua, et al. Experimental study of dynamic characteristics of sandstone under intermediate strain rate by using pendulum hammer driven “SHPB” apparatus[J]. Chinese Journal of Rock Mechanics and Engineering, 2014,33(12):2443-2450.

[5] 朱晶晶.循环冲击载荷下岩石力学特性与损伤模型的试验研究[D].长沙:中南大学,2012.

[6] 石祥超,陶祖文,孟英峰,等.致密砂岩Johnson-Holmquist损伤本构模型参数求取及验证[J].岩石力学与工程学报,2015,34(增刊2):3750-3758.

SHI Xiangchao, TAO Zuwen, MENG Yingfeng, et al. Calculation and verification for Johnson-Holmquist constitutive model parameters of tight sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2015,34(Suppl 2):3750-3758.

[7] 赵光明,谢理想,孟祥瑞.软岩的动态力学本构模型[J].爆炸与冲击,2013,33(2):126-132.

ZHAO Guangming, XIE Lixiang, MENG Xiangrui. A constitutive model for soft rock under impact load[J]. Explosion and Shock Waves, 2013,33(2):126-132.

[8] 李夕兵,左宇军,马春德.中应变率下动静组合加载岩石的本构模型[J].岩石力学与工程学报,2006,25(5):865-874.

LI Xibing, ZUO Yujun, MA Chunde. Constitutive model of rock under coupled static-dynamic loading with intermediate strain rate[J]. Chinese Journal of Rock Mechanics and Engineering, 2006,25(5):865-874.

[9] 梁书锋,吴帅峰,李胜林,等.岩石材料SHPB实验试件尺寸确定的研究[J].工程爆破,2015,21(5):1-5.

LIANG Shufeng, WU Shuaifeng, LI Shenglin, et al. Study on the determination of specimen size in SHPB experiments of rock materials[J]. Engineering Blasting, 2015,21(5):1-5.

[10] 吴帅峰.冲击荷载下砂岩损伤演化模型研究[D].北京:中国矿业大学(北京),2017.

[11] 魏明彬.拉普拉斯变换的作用及意义[J].成都师范学院学报,2013,29(1):101-105.

WEI Mingbin. Function and meaning of Laplace transform[J]. Journal of Chengdu Normal University, 2013,29(1):101-105.

[12] HALLQUIST J O. LS-DYNA key-word user’s manual[M]. California: Livermore Software Technology Corporation, 2003.

[13] 张安康,陈士海.LS-DYNA用户自定义材料模型开发与验证[J].计算机应用与软件,2011,28(4):71-73.

ZHANG Ankang, CHEN Shihai. Exploiting and verifying user-defined material model in LS-DYNA[J]. Computer Applications and Software, 2011,28(4):71-73.