合理低价D值分布规律实验研究

王 艳 王志君

(1.江西建设职业技术学院，江西 南昌 330200； 2.江西洪洲园林建设集团有限公司，江西 南昌 330000)

在清单计价规范合理低价中标原则的宏观指引下，各省、自治区、直辖市分别颁布了本省的合理低价算法，并制定了评标的具体实施细则。合理低价的分布规律一直是业界关心的问题，因为它的取值对中标结果的确定举足轻重。目前，国内基于概率论和数理统计方法研究人员较少，研究过程人为因素限制较多并忽略投标报价分布对中标结果的影响，采用公式推导只能得出一个具体报价，而实践揭示存在一个高概率中标报价区间。本文结合江西省现行合理低价评标办法，借助Matlab软件，实验完成均匀分布投标报价模式下合理低价D值分布情况，以窥视其中奥妙。

1 江西省合理低价法商务标评审概述

1)投标报价(A)大于招标控制价(M)值或小于[0.87(M-Z)+Z]值，该范围的投标报价为不响应招标文件的无效投标报价，失去参与平均值计算和中标排序资格。

2)投标报价(A)大于[0.97(M-Z)+Z]值并且不大于招标控制价(M)值，属于偏高投标报价，失去参与平均值计算和竞争中标人或中标候选人的资格。

3)投标报价(A)在不小于招标控制价[0.87(M-Z)+Z]值至不大于[0.97(M-Z)+Z]值以内时，即满足{[[0.87(M-Z)+Z]≤A≤[0.97(M-Z)+Z]]}，为合理竞争报价范围，合理竞争报价去掉1名～3名最低投标报价后，随机抽取1个～3个报价计算平均值AP。

4)计算合理低价D值。

(1)

其中，M为招标控制价；Z为招标暂列金额和暂估价(无该项内容时Z=0)；β为下浮让利系数，开标前从0.970，0.965，0.960，0.955，0.950，0.945，0.940 7个系数中随机抽取;μ为市场价格调整系数，开标前从0.980，0.975，0.970，0.965，0.960 5个系数中随机抽取一个;α为取费类别调整系数，查表可得。

5)确定中标候选人。

合理低价D值确定后，不小于D值的合理报价由低到高依次排序，最低投标报价排序第一，经评审中标排序人不足三家时，中标排序人数量自然减少。

2 商务标评审试算模型建立

2.1 模型条件

1)所有投标单位经评审合格，投标报价均为有效报价；

2)工程类别为三类，招标暂列金额和暂估价为0(Z=0)；

3)计算时，取招标控制价M=1，投标报价值为招标控制价下浮一定百分比，为招标控制价的相对值；

4)投标单位数假定50家。

受具体招标项目和竞标单位等因素的影响，最终的报价可能服从不同的分布，本文投标报价拟在合理竞争报价范围内服从均匀分布的基础上，展开对合理低价D值分布规律的研究。

2.2 建模

基于江西省颁布的合理低价评标法，运用Matlab软件编写程序建立评标法中商务标评审试算模型。该模型包含筛选合理竞争报价、确定合理低价D值、确定中标候选人以及绘制D值频率分布直方图等工作内容。建模过程如图1所示。

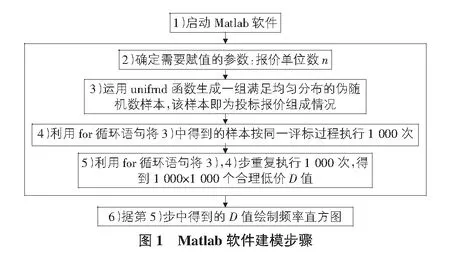
3 实验过程及结果

1)运行模型试算，得到n为50家时，Dn=50值的频率直方图见图2。

根据ABC法则，将D值的概率区间划分为A，B，C三类，其中A类为累积概率为0%～80%的区间，该区间是D值的主要分布区间，将其定义为投标保证区间。从图2可得D值在(0.895 7,0.926 9)区间的累积概率为80.4%，区间长度为0.031 2，该区间中点为0.911 3，运用插值法可算得，投标保证区间中点Xψ仍是0.911 3，投标保证区间长度L=0.031，投标保证区间为(Xψ-L/2,Xψ+L/2)，代入即为(0.895 8,0.926 8)。

2)合理低价D值的频率函数P。

曲线拟合是指选择适当的曲线类型来拟合观测数据，并用拟合的曲线方程分析两变量间的关系，运用Matlab曲线拟合工具箱CFtool拟合出在95%的置信区间下D值的频率函数，我们可以得到D的取值和对应的频率之间的关系。CFtool不仅可以绘制拟合后的曲线、给出拟合参数，还能给出拟合好坏的评价参数(Goodness of fit)，如SSE，R-square，RMSE等。其中，确定系数R-square是通过数据的变化来表征拟合的效果，它的正常取值范围为[0,1]，越接近1说明方程的变量对f(x)的解释能力越强，而方差SSE和标准差RMSE越接近于0，说明模型选择和拟合效果越好，数据预测越成功。

在95%的置信区间下合理低价D值的频率函数拟合结果可见表1(据表1可知：方差和标准差接近于0，确定系数接近于1，说明模型选择和拟合效果均较好)。其拟合函数为：

(2)

4 结语

本文首先运用Matlab软件编程，建立了基于均匀分布投标报价模式下江西省合理低价法商务标评审计算模型；然后借助如软件的曲线拟合工具箱CFtool，得到了投标保证区间为(0.895 8,0.926 8)和合理低价值D的频率函数；得出，在实际招投标过程中，具体问题具体分析是做出可靠决策的必要条件。

但是，本文只分析了基于均匀分布投标报价模式下合理低价D值的分布规律，而投标报价的分布实际可能服从多种分布情况，因此，还应对其他投标报价分布情况下的D值的分布规律做进一步研究。

参考文献：

[1] 张 旭,龙卫红.运用Excel电子表格建立建设工程投标报价试算模型[J].宁夏工程技术,2003(6):130-134.

[2] 刘连生.概率统计在投标报价决策中的应用[J].铁路工程造价管理,2003(6):19-21.

[3] 刘 伟.试论复合标底的投标报价方法和技巧[J].湖北农学院学报,2003(8):285-288.

[4] 于瑞庭.对复合标底投标报价的探讨[J].铁路工程造价管理,2005(5):28-31.

[5] 刘士兵.基于Simulink的高速铁路牵引供电系统仿真建模[J].华东交通大学学报,2013(6):59-61.

[6] 李向阳.复合标底报价的量化分析[J].铁路工程造价管理,2003(2):7-9.

[7] Khaled Nassar.Bradley University, “Pricing Construction Contracts in a Competitive Market:A Simulation Game” ASC Proceedings of the 38th Annual Conference. Virginia Polytechnic Institute and State University—Blacksburg, Virginia,2002:47-54.