预应力混凝土宽主梁斜拉桥成桥状态温度效应研究
李 博 张精卫
(1.中交第一公路勘察设计研究院有限公司,陕西 西安 710075; 2.中交通力建设股份有限公司,陕西 西安 710075)
桥梁结构在施工过程中容易受到外界因素干扰,在施工过程中产生施工偏差影响结构内部受力及成桥线性控制等,因此施工中需要事先分析影响结构成桥状态的影响因素,从而达到合理控制桥梁结构成桥状态与设计初始值相符合的要求[1]。斜拉桥施工过程中受环境、温度及施工工艺、荷载等因素的影响容易产生施工误差对成桥结构的内力及线性与设计状态产生偏差,影响斜拉桥结构的关键构件受力以及运营期间的长久持力性能。如何尽可能的降低或者消除大跨径斜拉桥在施工过程中的关键影响因素,保证斜拉桥的关键受力构件可以精确长久有效受力与桥梁接近或者吻合最初的设计值,是斜拉桥施工过程质量控制的精髓之处[3]。为减小施工误差对成桥结构的影响,必须考虑施工中对结构受力影响较大的关键因素,在施工中有效的消除其可能造成的影响。
温度场往往是个随机变量,与结构材料、位置、外界环境条件等密切相关而难以识别。结构温度场变化为非线性分布,温度变化引起结构的变形,且产生温度自约束应力和温度约束应力[2,4]。Fritz Leonhardt指出,箱型和板桥梁的顶底缘之间的温度差值可达到27 ℃~33 ℃[5]。因此,在大跨度斜拉桥桥梁施工控制中应考虑环境温度变化对结构关键构件受力及位移变化的影响[6]。预应力混凝土斜拉桥的主梁受环境温度变化的影响特别大,因此其施工过程的混凝土梁的标高控制往往比较困难。而温度变化相当复杂,包括日照温差、骤然温差、残余温度等影响。实测温度与理论温度值容易产生偏差,对施工中主梁竖向挠度控制造成影响,需要分析不同温度效应对斜拉桥索力及主梁线性的影响程度。其中,季节性温差使主梁、索和塔均匀升降温,而日照温度变化对结构关键构件如混凝土梁和斜拉索的受力及变形影响显著[7]。一般受日照平均温度变化的影响,混凝土梁和主塔容易在不同方向上产生不同位移以致发生挠曲变形;拉索受温度变化迅速,而主梁和主塔受外界温度变化缓慢,容易造成主梁、索塔、拉索之间产生温度差异。而且,这种温度差效应对于成桥状态结构的线性及内力影响不容忽视。
1 温度测点分布
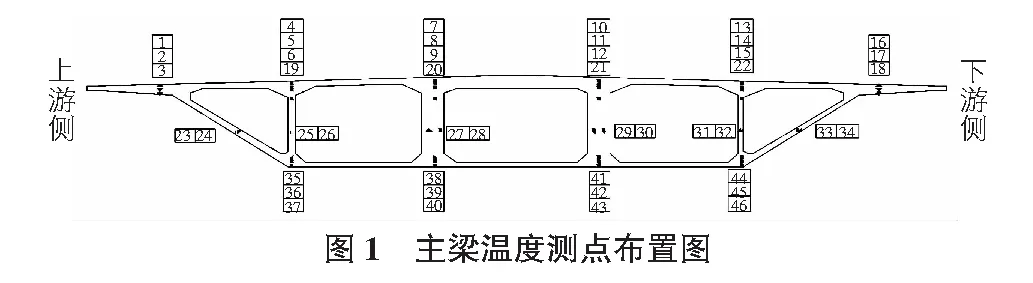
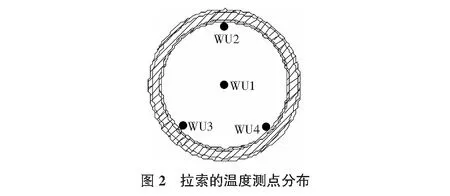
斜拉桥主梁梁宽41 m,底板宽21.6 m,梁高4.0 m。温度测试断面位于1号块、15号块,各测试断面内布置46个传感器,如图1所示。斜拉索的温度测点布置图如图2所示。
索塔高112 m,选取索塔a—a截面(距塔底30 m)、b—b截面(距塔底75 m)进行温度测试,索塔a—a截面温度测点布置如图3所示。混凝土结构物表面温度梯度较大,内部温度梯度较小,温度测点距表面的测点布置间距较小,距表面远的测点布置距离较大。

2 温度对结构成桥状态的影响
斜拉桥在施工环境中温度的变化对其成桥运营期间结构关键受力构件的干扰比较明显,计算温度效应对结构应力及位移的影响,确定温度效应对结构成桥状态的影响程度。选择桥面二期铺装后的半漂浮结构体系,分别对不同构件及组合结构的温度变化形式在有限元模型里面进行温度影响量化分析,考虑不同构件温度变化形式下的关键受力构件的受力及位移变化情况。
2.1 拉索与混凝土梁的温度差异影响
通过建立MIDAS有限元全桥模型,计算拉索与混凝土索梁之间的温度差异变化对索斜拉索索力的大小、混凝土宽主梁标高和混凝土主塔顶端的位移变化的影响。
由图4中变化规律可以看出,斜拉索与混凝土梁之间的温度差异变化对靠近混凝土索塔周边的短拉索以及斜拉桥跨中和边跨的长索的索力影响比较显著。当拉索索力与混凝土梁的温度差异变化为正值时,中跨部分Z9号~Z21号索力值增大,而斜拉索的其他索力值均减小。当索梁温差达到10 ℃时,Z1索的索力减小值最大为-129.32 kN,增加值最大为Z16的27.69 kN;温差变化值相反时,索力变化规律相反。当索梁温差变化幅度为10 ℃时,斜拉索B2号索力变化量最大是其设计成桥索力值的2.62%,因此索梁温差对成桥索力值的影响不容忽视。

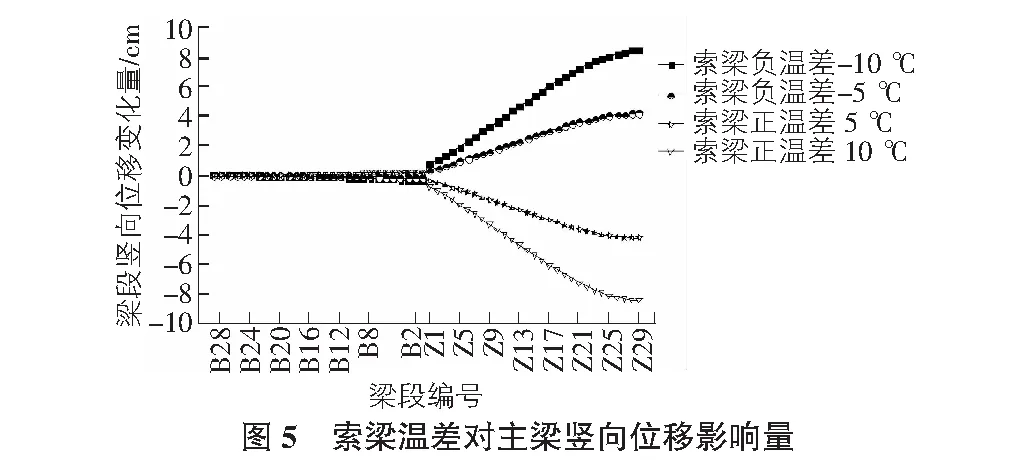
由图5可知,索梁温差变化对主梁竖向位移的影响成正比,且索梁温差对主梁中跨挠度影响值最大。其中,索梁负温差变化使中跨主梁竖向位移变大,索梁正温差变化使中跨主梁竖向位移变小,Z29号主梁对应的竖向位移变化最大,边跨主梁竖向位移变化较小。当温差变化为10 ℃时,Z29号主梁竖向位移变化值最大为8.47 cm。

表1 塔顶偏移与拉索和混凝土梁的温度差异的关系
由表1中的数据可以看出,混凝土主塔的塔顶端部位移变化受拉索与混凝土梁之间的温度差异值的影响较大,当索梁温差变化为8 ℃时,塔顶偏位值为16.82 mm。当索梁温差变化为正时,塔顶向中跨偏移;当索梁温差变化为负时,塔顶向边跨偏移。
2.2 混凝土梁竖向温度差异影响分析
通过建立全桥有限元模型计算分析拉索索力大小值、混凝土梁标高值变化及主塔顶端位移值的变化量。

由图6可知,当主梁竖向温度升温时,边跨两端端部的7对长拉索和中跨的跨中部分9对长索的索力逐渐增加,而靠近主塔周边的边跨和中跨部分的短索索力值逐渐减小。当混凝土梁的竖向温度差异降低10 ℃时,B12号索力增幅最大为19.06 kN,B28号索力减幅最大为29.47 kN。当主梁竖向温度增大时索力值减小,当主梁竖向温度减小时索力值增大。当主梁竖向温差变化10 ℃时,B5号索力的变化量最显著其索力的变化值仅为成桥阶段拉索设计索力值的0.59%。因此,混凝土梁的竖向温度差异值变化量对成桥阶段设计索力值的大小影响不明显。

由图7可知当主梁竖向温度升高时,边跨靠近端部的7段混凝土梁节段的竖向标高值减小,而边跨靠近主塔周边的混凝土节段的梁端标高增加;跨中靠近主塔周边的15节段混凝土梁的竖向标高值变大,而跨中部分其余的混凝土梁节段的标高值减小。当竖向温度增加10 ℃时,B28号主梁竖向位移最大减幅为0.45 cm,B28号主梁竖向位移增幅最大为0.23 cm,主梁竖向温度升温时其竖向位移值减小,主梁竖向位移受竖向温度梯度变化影响较小。
2.3 结构整体温度变化影响分析
通过建立全桥结构有限元计算模型,计算斜拉索索力大小的变化量、混凝土梁竖向标高的变化量及主塔塔顶端部的偏移量。
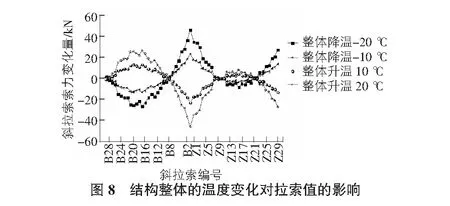
从图8中变化规律可以看出,结构的整体受环境的温度变化对靠近索塔部分短索的索力、跨中的短索的索力以及结构边跨部分跨中拉索索力的影响较大。当整体升温时,索塔7对拉索(B1号~B7号,Z1号~Z7号),中跨7对拉索(Z23号~Z29号)的索力大小值均逐渐减小,而其他的斜拉索索力值均逐渐增大。当结构的整体温度变化降低20 ℃时,拉索索力的大小最大增幅为46.13 kN,拉索索力的大小最大减幅为26.49 kN。当温差变化20 ℃时,B1号拉索索力的变化值最大为成桥索力值的0.92%。因此,整体升降温对成桥状态索力的影响较小。

从图9可知,当结构的整体温度升高时混凝土梁跨中的梁段的竖向标高值减小,变化量越大;而边跨位移增加,影响量较小。当整体降温20 ℃时,Z29号增幅最大为2.41 cm,B8号减幅最大为0.97 cm。整体降温时,主梁竖向位移变化量减小。
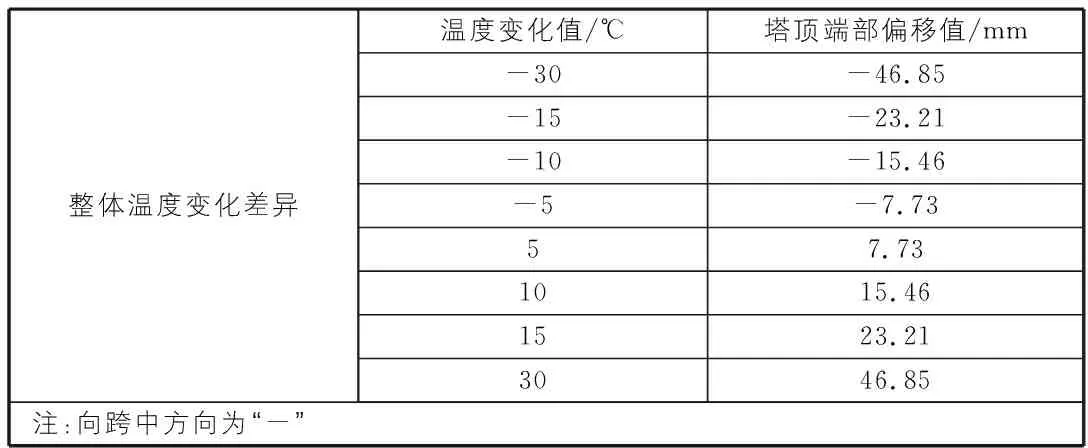
表2 整体升降温对塔顶偏移的影响
由表2中的数据可以看出,结构的整体温度变化对成桥阶段的索塔偏位的影响较大。当温度变化升高30 ℃时,塔顶向边跨偏移46.85 mm。中跨合龙一般选择在较低温度时合龙,合龙后体系升温,索塔向边跨偏移使中跨主梁标高增加达到设计成桥线性。
2.4 拉索与主塔温度差异影响分析
通过建立斜拉全桥有限元模型,计算分析拉索与混凝土梁之间温度差异对拉索索力的影响量、混凝土梁标高的变化量以及主塔塔顶端部的纵向偏移量。
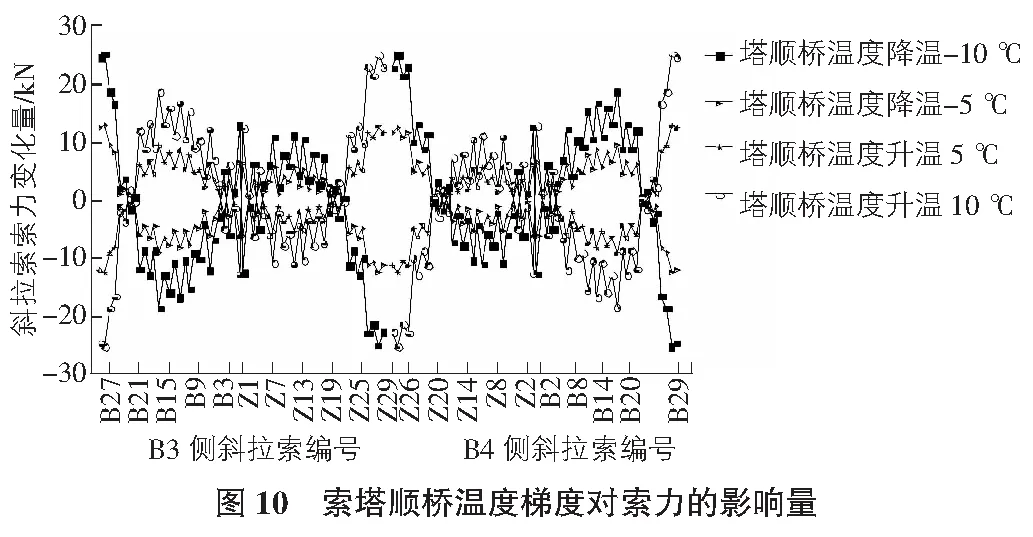
由图10可知,当索塔顺桥温度升温时,B3号、B4号索力值减小、增加变化规律及变化量相同。当索塔顺桥温度升温10 ℃时,B28号索力减幅最大为25.33 kN,B13号索力增幅最大为16.81 kN。当索塔顺桥向温度变化10 ℃时,B11号索力的变化值最大其变化量仅为成桥阶段设计索力值的0.38%。因此,混凝土梁的竖向温度变化差异对成桥阶段的拉索索力的影响不明显。

从图11可知,当索塔顺桥温度降温时,B3号与B4号主梁的位移增加、减小变化规律及变化量相同。当索塔顺桥温度升温10 ℃时,位移最大减幅为0.42 cm,最大增幅为0.42 cm。因此,主梁竖向位移受索塔顺桥温度变化影响较小。

表3 索塔顺桥温度梯度对塔顶偏移的影响
由表3可知,索塔顺桥温度差异变化对成桥阶段的主塔塔顶端部的偏移量影响比较显著。当拉索与主塔之间的温度差异变化值达到8 ℃时,其主塔的塔顶水平偏位最大值为74.09 mm。因此,在斜拉桥合龙施工中应选择温度变化较小时间合龙。
3 结语
1)大跨径宽主梁斜拉桥整体结构的不同组合温度效应对结构成桥阶段的拉索索力的影响均比较小,最大变化量是受拉索与混凝土梁之间的温度差异的影响仅为成桥索力值的2.62%。2)混凝土梁 斜拉桥施工过程标高控制是保证运营期间行车平顺舒适的关键,各种温度变化差异工况中拉索与混凝土梁之间温度差异对混凝土梁标高的影响最显著。因此,混凝土梁合龙的时候要选择夜间温度变化较小的时间进行。3)混凝土主塔塔顶偏位影响主塔的结构受力安全以及运营阶段桥面线性下沉挠曲影响行车舒适性,特别是大跨径混凝土斜拉桥纵向温度差异对其塔顶的纵向偏移影响最显著。因此,在混凝土梁合龙的时候要考虑混凝土塔纵向温度差值的影响,减小成桥阶段的影响。
参考文献:
[1] 陈德伟,郑信光,项海帆.混凝土斜拉桥的施工控制[J].土木工程学报,1993,26(1):7-9.
[2] 喻正富,张筱雨,刘来君,等.基于遗传算法的大体积混凝土热力学参数反演分析[J].建筑科学与工程学报,2015,32(5):81-88.
[3] 陈德伟,许 俊,周宗泽,等.预应力混凝土斜拉桥施工控制新进展[J].同济大学学报,2006,29(1):99-103.
[4] 刘兴发.混凝土结构的温度应力分析[M].北京:人民交通出版社,1991.
[5] 陈衡治.预应力混凝土箱梁桥的温度场和应力场[J].浙江大学学报(工学版),2005,39(12):1885-1890.
[6] 刘兴发.预应力硷箱梁温度应力计算方法[J].土木工程学报,1986,19(1):46-56.
[7] 马文田,韩大建.混凝土斜拉桥施工控制的最佳成桥状态法[J].华南理工大学学报(自然科学版),1999,27(11):1-2.

