软黏土蠕变模型研究综述
董 皇 帅
(浙江工业大学建筑工程学院,浙江 杭州 310023)
0 引言
软黏土在我国沿海、沿江地区广泛分布。工程实测表明,建造于软土地区的建筑工程沉降不仅取决于外荷载施加时产生的瞬时变形,也依赖于工后沉降变形。软土工程的工后沉降变形,与软土的蠕变特性密切相关。软黏土的蠕变定义为在恒定外荷载持续作用下,变形随时间发展的现象,是软黏土重要的力学特性之一。一般地,土体蠕变特指土体主固结结束后变形随时间发展的过程。
为了能够合理反映软黏土的蠕变特性,国内外许多学者开展了软黏土蠕变模型的研究。根据各种蠕变模型特点,大致分为四类:一是经验或半经验模型;二是元件模型;三是黏弹塑性模型;四是分数阶导数模型。
1 经验—半经验模型
经验—半经验模型的本质是在软黏土室内外的蠕变试验数据基础上,经统计分析后获得的适用于某类土质的具有一定实用价值的经验公式。
最早的经验或半经验模型由Taylor[1]提出,其表达式如下:
(1)
后来,人们发现土在侧限蠕变中土的二次压缩系数正比于压缩指数。在此基础上,Mesri等[2]提出了下式蠕变模型:
(2)
此蠕变模型可考虑压缩指数,能够反映外界荷载应力影响下软黏土蠕变的变化规律。
为了考虑软黏土蠕变的非线性性质,Singh和Mitchell[3]提出了三参数蠕变模型:
(3)
由于该模型参数意义明确,数量少,之后迅速得到推广应用。不少学者还对其适当改动得到了适用于不同地区的软黏土蠕变模型。如:王常明等[4]在此基础上提出了适用于滨海软黏土的流变模型。需要指出的是,这个蠕变模型只适合于软黏土一维固结蠕变情况。
Kavazanjian和Mitchell[5]通过软黏土蠕变试验,测试了软黏土的体积应变,通过试验结果分析研究发现,软黏土在蠕变阶段的体应变可表示为:
(4)
何利军等[6]针对湛江软黏土系统开展了三轴固结不排水蠕变实验,得到不同围压、不同加载路径下的全过程蠕变曲线,得出应力—应变关系采用线性函数来拟合,而应变—时间关系采用双曲线函数来拟合的结论。
2 元件模型
该类蠕变模型的基本思想是组合理想的元件,形成各种不同模型,由各组合元件的基本性质属性以及组合关系,推导出软黏土蠕变模型。然后,通过试验资料来确定蠕变模型中的各个参数值。元件模型的最大特点是每个元件的物理含义清楚,模型本身比较直观、形式相对简单。元件模型大致有两类:一是微分型流变本构模型;二是积分型流变本构模型。
微分型流变本构模型的代表模型是Kelvin模型。张敏江等[7]对某地区粉质黏土开展了蠕变试验研究,遵循简化非线性流变模型的建模方法,对Kelvin模型进行改造而建立了非线性Kelvin模型。潘晓明等[8]在西原模型的基础上,引入非线性的Kelvin元件以及非线性Bingham黏塑性元件,建立能完整反映蠕变全过程的非定常西原黏弹塑性流变方程,利用有限元模拟结果可知,所建立的模型具有广泛的使用性。
积分型流变本构模型,是根据蠕变方程ε=J(t)σ0和Boltzman叠加原理,经过一定的数学运算可以得到一维积分型流变本构方程,典型的表达式为:
(5)
3 黏弹塑性模型
黏弹塑性模型是在经典弹塑性理论基础上结合相关黏性理论发展起来的软黏土蠕变模型。在此类模型中把塑性势等同于蠕变势。黏弹塑性模型大致有两类:一是过应力理论模型[9];二是非稳态流动面模型[10]。前者是通过应力函数求黏塑性应变,而后者通过应变函数求黏塑性应变。
总应变可以分解为弹性应变和黏塑性应变之和,如式(6)所示:
(6)
式中:εij——总应变;


此外,根据弹性胡克定律,可求得弹性应变增量,而根据黏塑性定律,可求得黏塑性增量。
在过应力理论中,流动法则为:
(7)
式中:ζ——流动性的参数;
<>——MacCauley符号;
F——过应力函数;
φ(F)——材料的黏性核;
g——势函数;

黏性核φ(F)具有如下性质:
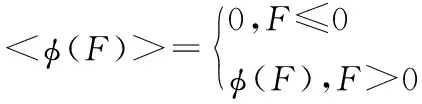
(8)
过应力函数F为当前应力状态距静态极限面之间的距离。
在非稳态流动面模型中,所选用的流动法则为:
(9)
其中,Λ是一非负的系数,可用式(10)表示:
Λ=Λ1+Λ2
(10)
其中,Λ1与塑性理论的流动因子相同;Λ2为黏性对黏塑性应变的影响。
4 分数阶导数模型
近年来,分数阶导数由于其自身具有的显著优势,成为众多数学领域中发展较为迅速的一个分支。相比于整数阶导数,分数阶导数具有以下优势[11]:
1)不同于整数阶导数,分数阶导数描述的特点是具有“记忆”性,因此可以描述带有全局性的现象;
2)与同样能描述整数阶导数的非线性方法相比,分数阶导数在描述复杂问题时其物理意义更明确,表达更简洁。
Yin等[12]采用了变阶数分数阶元素,构建了可考虑土体内部孔隙水运动对土体蠕变性状的影响的软黏土蠕变模型,通过数值模拟验证了该软黏土蠕变模型可以描述孔隙水在软土蠕变过程中的孔隙水运动过程,并可反映实际的软土力学演化规律。李锐铎等[13]利用分数阶导数构建了一个描述软黏土的五元件模型。该模型在低应力水平下关闭变系数粘壶描述稳定和衰减蠕变;在高应力水平时打开变系数粘壶,描述加速蠕变。最后利用上海软黏土进行了拟合验证。刘朝辉等[14]提出一个分数阶蠕变模型,该模型将Abel粘壶元件替换黏弹性模型中牛顿粘壶,得到含分数阶导数的标准线性体,通过实验分析结果表明该标准线性体能够很好地描述软黏土的松弛和蠕变现象。胡华[15]通过试验指出淤泥质软土在动载作用下具有黏弹塑性力学行为,并经过理论分析,建立淤泥质软土的黏弹塑性力学模型,推导了新的流变方程和黏弹塑性力学参数。结果表明,黏弹塑性参数与动态剪切模量有很大关系。何利军[16]提出了一种新的蠕变核函数的选取方法,即用Burgers模型的导数形式作为核函数,并探讨了该蠕变模型能精确反映软黏土蠕变规律的原因;模型参数少,物理意义明确,适用性较强。
5 结语
针对软黏土的蠕变特性,国内外学者开展了大量的研究工作,并提出了许多不同类型的软黏土蠕变模型。由于软黏土具有很强的区域性特点,各种蠕变模型都有自身的适用性,在应用时需要根据实际情况进行选择。其中也存在一些不足,比如:
1)实际工程中为了安全考虑常采用分级加载,由于前一级加载会对后一级加载产生影响,进行分别加载条件下的蠕变特性研究是非常具有意义的。目前,关于考虑分级加载情况的软黏土蠕变模型还比较少。
2)目前很少有学者开展加载再卸载试验的软黏土蠕变试验研究,而超载预压是软土地基的常用地基处理方法,在实际工程中存在着大量先加载后卸载情况的软土地基蠕变问题,因此针对加载再卸载情况下软土的蠕变规律需要进一步的研究。
3)目前大多数的软黏土蠕变模型是针对从加载开始至试验结束的软黏土全过程蠕变模型,这包含了土体孔压消散阶段的固结过程。由于没有区分主固结和蠕变两个阶段,这种软黏土蠕变模型在计算的蠕变量就会包含固结阶段的变形量,导致蠕变计算量偏大。在实际工程中,软黏土蠕变过程主要是发生在土体主固结结束后,此时土体孔隙水压力不再消散。为了反映实际情况,有必要构建只考虑主固结结束后软黏土蠕变阶段的软黏土蠕变模型。
参考文献:
[1] Taylor D W. Research on consolidation of clays[R].Massachusetts, Cambridge: Department of Civil Engineering, MIT,1942.
[2] Mesri G, Febres-Cordero E, Shields D R, et al. Shear stress-strain-time behaviour of clays[J]. Geotechnique, 1981,31(4):537-552.
[3] Singh A, Mitchell J K..General stress-strain-time function for soils[J]. Journal of the Soil Mechanics and Foundation Division,1968,94(1):21-46.
[4] 王常明,王 清,张淑华.滨海软土蠕变特性及蠕变模型[J].岩石力学与工程学报,2004,23(2):227-230.
[5] Kavazanjian E., Mitchell J. K..Time-deformation behavior of clays[J]. Journal of the Geotechnical Engineering Division,1980,106(6):611-630.
[6] 何利军,孔令伟,张先伟,等.湛江软黏土蠕变特性及经验模型[J].水文地质工程地质,2011,38(1):59-64.
[7] 张敏江,阎 婧,初红霞.结构性软土微观结构定量化参数的研究[J].沈阳建筑大学学报(自然科学版),2005,21(5):455-459.
[8] 潘晓明,杨 钊,许建聪.非定常西原黏弹塑性流变模型的应用研究[J].岩土力学与工程学报,2011,30(S1):2640-2645.
[9] DesaiI C S, Zhang D. Viscoplasic model for geological materials with generalized flow rule[J].International Journal of Numerical and Analytical Methods in Geomechanics,1987,11(6):603-620.
[10] Lingaard M, Augustesen A, Lade P V.Characterization of models for time-dependent behavior of soils[J].International Journal of Geomechanics,2004,4(3):157-177.
[11] 王玉娇.分数阶导数及其应用[D].太原:太原理工大学,2014.
[12] Yin Deshun, Li Yanqing, Wu Hao, et al. Fractional descrip tion of mechanical property evolution of soft soils during creep[J].Water Science and Engineering,2013,6(4):446-455.
[13] 李锐铎,乐金朝.基于分数阶导数的软土非线性流变本构模型[J].应用基础与工程科学学报,2014,22(5):856-864.
[14] 刘朝辉,张为民.含分数阶导数的粘弹性固体模型及其应用[J].株洲工学院报,2002,16(4):23-25.
[15] 胡 华.动载作用下淤泥质软土流变模型与流变方程[J].岩土力学,2007,28(2):237-240.
[16] 何利军,孔令伟,吴文军,等.采用分数阶导数描述软黏土蠕变的模型[J].岩土力学,2011,32(S2):239-244.

