工程岩体材料粘弹塑性损伤力学模型
汪 灿
(中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
1 概述
损伤就是指材料在一定应力状态下其力学性能劣化的现象[1]。岩石材料的蠕变损伤表现为变形与时间效应的耦合,蠕变变形发展到一定的量值后,其蠕变变形的速率表现为和时间及累积变形密切相关的特点。陈卫忠等[2]认为盐岩的蠕变速率不仅与时间相关,而且还与累积蠕变变形密切相关;范庆忠等[3]建立了同时考虑蠕变硬化和蠕变损伤的非线性蠕变损伤本构模型;杨春和陈锋[4]建立了能够反映盐岩蠕变全过程的蠕变损伤本构模型;陈锋等[5]通过采用能够反映偏应力和围压影响的损伤因子,建立了新的蠕变损伤本构模型;蒋昱州等[6]建立了以应力水平与时间为变量的损伤演化方程。
根据损伤力学基础理论,考虑到岩石变形过程中裂纹萌生与发展是损伤的诱因,建立蠕变参数随时间损伤演化方程,将损伤变量引入到Cvisc元件模型中,建立岩石蠕变损伤本构模型,并通过数值模拟验证模型的有效性。
2 Cvisc蠕变损伤模型
2.1 考虑参数损伤的Cvisc元件模型
Cvisc元件模型[7,8]能够较好地描述软岩粘弹塑性蠕变特征。为了描述参数损伤特征,在建立蠕变模型时引入损伤因子ωS,最终得到考虑损伤的粘弹塑性蠕变损伤模型。该模型由Maxwell损伤体、Kelvin损伤体以及Mohr-Coulomb塑性体组成(见图1)。
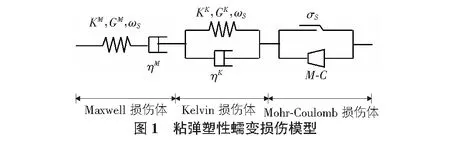
图1中KM,KK分别为Maxwell体和Kelvin体中弹簧元件的体积模量;GM,GK分别为Maxwell体和Kelvin体中弹簧元件的剪切模量;ηM,ηK分别为Maxwell体和Kelvin体中的粘性系数;ωS为参数损伤演化因子。
在进入塑性屈服阶段之前,砂岩处于粘弹性阶段,其蠕变方程为球应力与应力偏量两种应力状态下Maxwell体和Kelvin体粘弹性应变的叠加,进入塑性阶段后,模型中的Mohr-Coulomb塑性元件开始发挥作用。
2.2 三轴蠕变加卸载试验
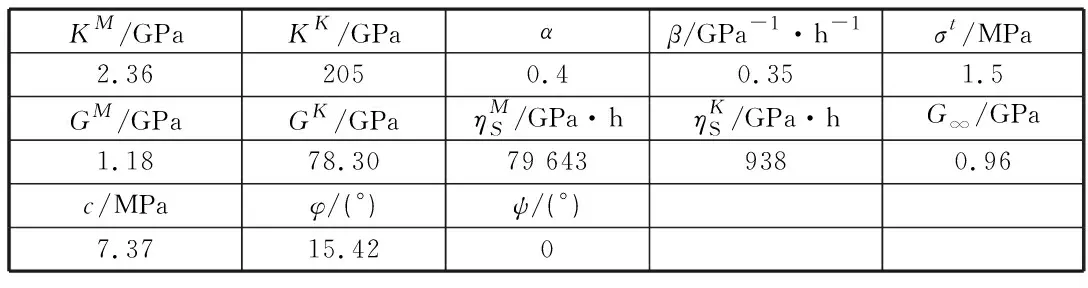
为了衡量蠕变过程中力学参数的损伤程度,开展了不同围压不同偏压下的砂岩蠕变试验,并在蠕变过程中的若干个时间点进行轴压卸载,以此获得不同时刻下的弹性力学参数。具体试验荷载条件和卸载方式如表1所示,在5个不同围压和不同轴向偏压的蠕变试验条件下选择18个左右的卸载时刻进行轴压卸载再加载,即将其当前的轴向偏压力(σ1-σ3)按照0.2 MPa/s的速率卸载到0,再按照相同的速率加载到蠕变应力水平。根据各个卸载时刻的应力应变数据可以得到干燥砂岩岩样的体积模量和剪切模量,如图2所示。

表1 三轴蠕变加卸载试验中砂岩岩样编号及其荷载条件和卸载速率

由图2可以看出,在给定围压和偏压下多孔砂岩的体积模量初始值差异较剪切模量大,但体积模量在蠕变过程中的变化不明显,不存在显著的随时间逐渐减少的特征,然而剪切模量相比较起来就具有明显的随时间损伤弱化的特点,而且围压越小,偏压力越大的情况下这种弱化的趋势越明显。
2.3 应力偏量下的参数损伤演化规律
试验结果体积模量不同于剪切模量,不会显著的随时间逐渐减少,这是因为在球应力作用下,无论是无损岩体还是已经发生损伤的岩体,其中的微孔隙、微裂隙会发生闭合没有弱化特征,而在应力偏量作用下,砂岩内部微裂纹发生扩展,新裂纹开始萌生,导致砂岩力学参数的弱化。因此,在考虑损伤效应的粘弹塑性蠕变损伤模型中,主要讨论应力偏量作用下的粘弹性参数损伤演化规律。
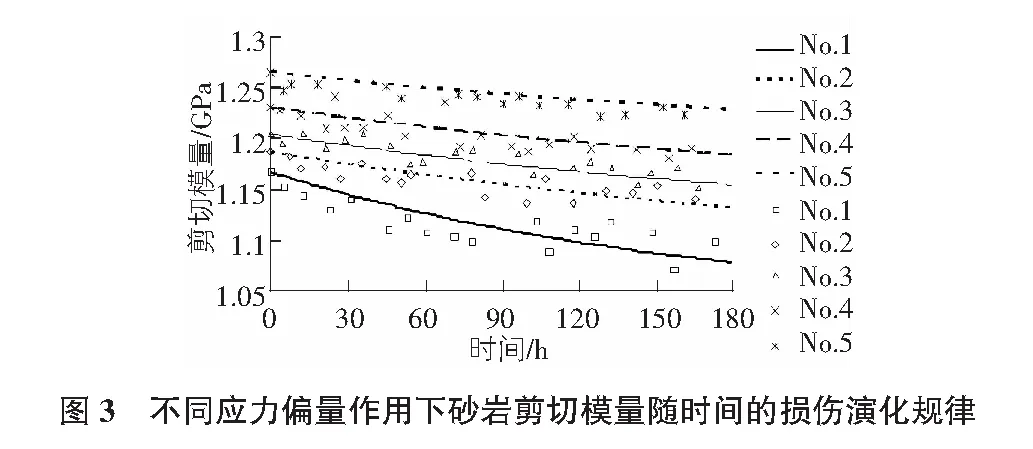
基于应变等效原理,以剪切模量变化定义应力偏量分量下的粘弹性参数损伤演化因子。假设剪切模量和剪切粘性系数遵循一致的损伤演化规律。根据损伤的定义和蠕变参数演化过程,假设多孔砂岩的粘弹性参数中的剪切模量G是由初始剪切模量G0向长期剪切模量G∞( 根据本文2.2试验结果,利用最小二乘法对损伤演化因子公式曲线和试验实测值进行拟合求得系数α=0.4,β=0.35 GPa-1·h-1,得到剪切模量在不同应力状态作用下随时间的演化曲线如图3所示,散点为试验实测值,曲线为公式拟合值。不同应力状态下拟合的相关系数如表2所示。 表2 不同应力状态下砂岩剪切模量损伤演化规律拟合曲线的相关系数 编号No.1No.2No.3No.4No.5围压/MPa510152030轴向偏压/MPa1718192021相关系数0.828 80.823 40.871 30.904 30.888 9 偏应力为零时,G∞=G0剪切模量没有发生损伤;随着偏应力的增加,砂岩损伤程度逐渐加大,其长期剪切模量不断减小,当偏应力达到峰值(σc-σ3)时,砂岩破坏,此时长期剪切模量等效为岩石破坏后的残余剪切模量。 通过FLAC3D二次开发,根据本文参数损伤演化方程在Cvisc模型基础上修改了.h和.cpp文件,其生成的动态链接库dll文件在计算过程可被主程序调用。在调用前应把该自定义模型输入到“FLAC3D.INI”中,以避免每次调用该模型时都需进行dll的配置。按照图4流程图开发Cvisc损伤蠕变模型。 数值计算中设定试件尺寸为高100 mm,直径50 mm的圆柱体。共划分1 000个单元、1 111个节点。模型在底部设定Y方向上的约束,施加5 MPa的等向围压以及10 MPa的轴向偏应力。通过本文所述方法获取模型参数如表3所示。该本构模型的数值模拟曲线与试验数据曲线如图5所示。当本模型不计参数损伤时,则退化为图5中“退化模型”。 表3 模型参数 由图5可以看出,本文模型由于考虑了参数损伤更加吻合试验值,其退化模型低估了应变值,偏离实测试验值。 对于复杂岩土结构的粘性特征,在不同应力分量作用下表现出不同的蠕变特性。由于在球应力作用下,微孔隙和微裂纹发生闭合且没有新的裂纹产生,也不存在明显的参数弱化。在应力偏量作用下,已有的裂隙发生扩展并且萌生新裂纹,导致力学参数弱化。因此,本文主要讨论了应力偏量作用下的蠕变参数随时间的演化规律。基于应变等效原理,以剪切模量变化定义应力偏量分量下的蠕变参数损伤演化因子。在此基础上建立的砂岩蠕变损伤模型考虑了蠕变参数在应力偏量作用下的参数损伤演化规律。此外,根据FLAC3D所提供的二次开发接口,开发了该模型的程序流程图。通过算例验证了该模型具备模拟岩石材料蠕变力学参数损伤的功能。该模型可以更准确地描述岩土这类损伤材料的蠕变特征,进一步完善材料的流变模型。 参考文献: [1] 谢和平.岩石混凝土损伤力学[M].北京:中国矿业大学出版社,1990. [2] 陈卫忠,王者超,伍国军,等.盐岩非线性蠕变损伤本构模型及其工程应用[J].岩石力学与工程学报,2007,26(3):467-472. [3] 范庆忠,高延法,崔希海,等.软岩非线性蠕变模型研究[J].岩土工程学报,2007,29(4):505-509. [4] 杨春和,陈 锋.盐岩蠕变损伤关系研究[J].岩石力学与工程学报,2002,21(11):1602-1604. [5] 陈 锋,杨春和,白世伟.盐岩储气库蠕变损伤分析[J].岩土力学,2006,27(6):945-949. [6] 蒋昱州,徐卫亚,王瑞红,等.岩石非线性蠕变损伤模型研究[J].中国矿业大学学报,2009,38(3):331-335. [7] Pellet F.,Roosefid M.,Deleruyelle F..On the 3D numerical modelling of the time-dependent development of the damage zone around underground galleries during and after excavation[J].Tunnelling and Underground Space Technology,2009,24(6):665-674. [8] Bonini M.,Debernardi D.,Barla M.,et al.The mechanical behaviour of clay shales and implications on the design of tunnels[J].Rock mechanics and rock engineering,2009,42(2):361-388.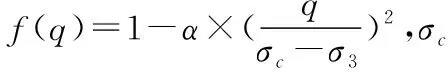

3 模型的数值分析


4 结语

