某拖车停车楼的结构鲁棒性定量分析

高 扬

(上海市政工程设计研究总院(集团)有限公司，上海 200092)

结构鲁棒性是指结构在突发局部损伤的情况下不致发生不成比例破坏的能力[1]。相比于结构所遭受的常规荷载，突发事件具有更高的不确定性和更大的潜在危险。这意味着，结构安全性已不能仅靠增加构件的安全储备和加强施工的安全监管来保证，还需要从结构系统的层面强调节点和构件连接等拓扑关系的合理性[2]。

尽管拖车停车楼在传统设计方法和建造工艺上与一般框架结构或框架剪力墙结构无异，但是从鲁棒性的角度看，这类结构仍存在较高的安全风险。这是因为拖车具有较大质量，不论是由于人为失误还是人为主动破坏，都可能因撞击而对柱产生较大初始损伤；同时，因为拖车体积大、车身长，停车楼不论是停车区还是行车区都往往采用大间距柱网布置，减少了冗余的传力路径。

本文针对某拖车综合服务中心的一栋停车楼进行鲁棒性分析，定量评估结构的鲁棒性，寻找其中最关键的构件，并考察结构鲁棒性与其层数、行车区跨度等之间的关系，以期对实际工程产生指导意义。

1 工程概况

某拖车停车楼长112.8 m，宽104.7 m，层高6.6 m，地上9层，建筑总高度60 m，无地下室。停车区标准柱网为13 m×8 m，柱截面为1 000 mm×1 000 mm；X方向框架梁截面为400 mm×1 000 mm，设置两道次梁；Y方向框架梁截面为500 mm×1 200 mm。行车区柱网为13 m×19 m，柱截面为1 000 mm×1 300 mm；X方向框架梁截面为800 mm×1 350 mm；Y方向框架梁截面为600 mm×1 300 mm，设置三道次梁。

结构的三维模型和标准层平面布置图分别见图1，图2。

2 鲁棒性理论

通过对结构引入合理扰动，并考察各节点间相互作用的改变来定量评估结构的鲁棒性。基本假定：1)突发事件不和极端的自然灾害同时发生，且仅作用在结构的构件上；2)结构受扰动前后均处于线弹性小变形工作状态。

对应于突发事件引起构件刚度退化，将“结构扰动”定义为各构件截面面积的微小变化。将所有构件的截面面积集成为：

Ae=[A1A2…Ae…Am]T

(1)

则结构扰动就可表示为：

dAe=[dA1dA2… dAe… dAm]T

(2)

其中，Ae为构件e(e=1,2,…,m)的截面面积;dAe为相应构件截面面积的改变；m为构件数目。

对应于突发事件引起的间接后果为节点间相互作用的变化，包括节点间力和变形传递机制的改变，将“节点间相互作用的改变”定义为节点势能的改变。将所有节点的势能集成为：

Ev=[E1E2…Ev…En]T

(3)

则结构受扰动引起的节点势能变化为：

dEv=[dE1dE2… dEv… dEn]T

(4)

其中，Ev为节点v(v=1,2,…,n)的势能;dEv为相应节点势能的改变；n为节点数目。

结构鲁棒性衡量的是系统抑制扰动在其内部放大的能力，即所有扰动与对应结构节点间相互作用改变之间比值的下限。以结构未受扰动时的状态为初始状态，则结构鲁棒性指标为：

(5)

其中，║·║2为向量2-范数，为相应物理量的一种量化；║dAe║2/║Ae║2,║dEv║2/║Ev║2分别反映扰动的局部程度和结构性能改变的程度。

根据作者已有的研究成果[3]，可以建立结构扰动dAe和节点势能变化dEv之间的关系：

dEv=HdAe

(6)

其中，H=B(Z1+Z2+Z2)为传递矩阵；B为节点与构件关联关系的矩阵表示，其第v(v=1,2,…,n)行第e(e=1,2,…,m)列的元素Be为：

(7)

矩阵Z1,Z2和Z3的表达式分别为：

(8)

(9)

(10)

其中，ke,de和UeF分别为构件e的刚度矩阵、节点位移和构件两端固支时的应变能；a为结构外荷载和构件内力间的转化矩阵；κ为由构件轴向、抗侧和抗弯(扭)刚度组成的矩阵；K为结构总刚矩阵；D为结构节点位移；T为节点自由度从整体坐标系到各构件局部坐标系的对应关系；(■)′为对相应构件截面面积求导。

H中第v行第e列的元素Hve表示由构件e的单位扰动所引起的节点v的势能变化，它显示了构件e对节点v的影响程度。第e列的列向量He表示由构件e的单位扰动所引起的结构所有节点势能的变化，它显示了构件e对整个系统的影响程度；采用列向量的2-范数║He║2将其量化，并称之为构件e的重要性。重要性大的构件在遭受突发损伤时往往能引起很大的结构节点的势能改变，因而其正反映了结构的关键部位所在。矩阵H表示各构件扰动和各节点势能变化之间关系的一种分布。由矩阵相容2-范数║H║2的数学定义，并结合式(5)可得结构鲁棒性的指标为：

(11)

3 结构鲁棒性分析

为简便，这里将结构视为由8个相同的标准层组成，第9层结构以荷载的形式传给下层柱网。在分析时，考虑结构仅受竖向荷载作用，并只计算各柱和主梁的重要性。

各楼层所受恒荷载除梁板自重外取4 kN/m2，活荷载取10 kN/m2；顶层所受恒荷载除梁板自重外取7 kN/m2，活荷载取2 kN/m2。认为楼板所受面荷载以梯形分布或三角形分布传递给梁。构件编号原则为：从底层到高层，编完一层构件再到上一层；各层之中先编柱、后编Y方向梁、最后编X方向梁。

3.1 结构鲁棒性计算

计算得到结构的║H║2,║Ae║2和║Ev║2分别为18.12 kN·m/m2，39.15 m2和218.6 kN·m，结构的鲁棒性指标IR=0.308 2。从传递矩阵H可以进一步得到结构各构件的影响性，见图3。

从上述结果可以看出：柱的重要性一般比梁大，下层柱的重要性又比上层柱大，这符合在竖向荷载作用下的结构受力特点，荷载经由梁传递给柱，并自上而下汇聚于下层柱，下层柱成为了重要的传递荷载的路径。在同一层中，行车区域的柱更为重要，该区域柱网间距大，传递竖向荷载的冗余路径较少，柱子支撑着更多的上层结构，因而存在更多的潜在危险。底层行车区域的柱重要性最大，构成结构的致命缺陷，针对这几个构件的突发局部破坏很可能会引起最不成比例的后果。

3.2 结构鲁棒性与层数的关系

保持平面布置和构件尺寸不变，考虑结构在不同层数下的鲁棒性变化情况，见图4。

由图4可以看出，增加结构层数对其鲁棒性不利。这是因为层数的增加使得框架柱和框架梁的数量增加，框架的竖向荷载相应增加，越往下层，汇聚而来的荷载越大，构件的重要程度将越发突出。同时从图4中还可以看出，随着层数的增大，结构鲁棒性减小的幅度降低。这是因为当建筑很高时，结构拓扑关系越发接近，结构鲁棒性的差别也相应减小。

3.3 结构鲁棒性与跨度的关系

保持层数和构件尺寸不变，考虑结构在不同行车区跨度下的鲁棒性变化情况，见图5。

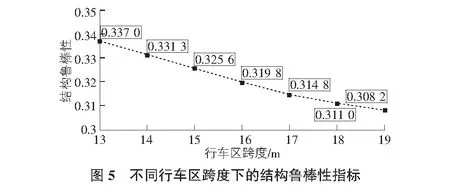
由图5可以看出，增加行车区结构跨度对结构鲁棒性是不利的。考虑到拖车的转弯半径，行车区域往往不可避免采用较大柱网布置。随着跨度的增大，这个区域内需要往下传递的荷载不断增加，而柱的数量并没有相应变多，所以柱作为传递荷载的路径以及保证上层结构不致垮塌的一道防线的重要性不断增加。从系统的层面来看，这些柱子构成了结构“牵一发而动全身”的致命缺陷，并随柱距的增大而愈发凸显，因而结构的鲁棒性不断下降。

4结语

1)采用已有的结构鲁棒性理论，对某拖车停车楼的实际工程进行鲁棒性分析。通过寻找传递矩阵中2-范数最大的列向量所对应的构件来确定结构的关键部位，利用矩阵2-范数的性质来量化结构抑制扰动在其内部放大的能力，从而定义结构的鲁棒性指标。

2)分析各层各类型构件产生重要性差异的原因，对比结构鲁棒性在不同层数及不同跨度下的变化情况，指出层数及跨度的增大都将使结构底层尤其是行车区相应柱的重要程度过于突出，从而降低结构的鲁棒性。

参考文献：

[1] 刘西拉.结构工程学科的进展与前景[M].北京:中国建筑工业出版社,2007:139-140.

[2] MENZIES J.Structural safety 1994-96:eleventh report of SCOSS[J].Structural Engineering International,1997,7(2):122-124.

[3] 高 扬.结构鲁棒性定量分析及其在地下框架结构中的应用[J].建筑结构学报,2018,39(1):153-161.