基于L1自适应控制的同步发电机励磁系统自动调节器

赵梦莹

哈尔滨电机厂 哈尔滨 150080

1 设计背景

励磁系统是电力系统中同步发电机的重要组成部分，是向发电机提供转子直流励磁电流的一种自动装置。励磁系统自动调节器，也称励磁系统控制器，是励磁系统的核心部件，通过调节励磁功率装置中的励磁电流来保证发电机输出电压的平稳性。由于发电机输出电压不可避免地会受到外界环境的影响，负载的频繁切换和波动，也会导致发电机的模型参数产生摄动，因此励磁系统自动调节器应具有克服环境和发电机系统不确定性的能力。

针对上述问题，许多学者进行了探索。文献[1]利用非线性微分几何控制和H∞控制理论，针对水轮发电机组设计了非线性鲁棒调节器。文献[2]基于H∞干扰抑制方法，提出了一种鲁棒分散控制策略，基于该策略设计了汽轮发电机和水轮发电机的调节控制器，实现了相应的分散稳定控制。文献[3]基于H∞状态反馈控制，提出了一种自动电压调节器，可明显改善励磁系统的鲁棒性。

笔者基于L1自适应控制[4]进行同步发电机励磁系统自动调节器的设计，所设计的不确定系统具有较好的自适应性和鲁棒性。

2 同步发电机和励磁功率装置数学模型

励磁系统包括励磁对象(通常为同步发电机)、励磁功率装置(通常为由晶闸管构成的整流电路)、测量元件和调节器等部分。为简化设计，可忽略测量元件的动态变化，将其假设为常值传递函数，而同步发电机和励磁功率装置的动态特性则不能简单忽略。为进一步优化励磁系统自动调节器的设计，需要建立同步发电机和励磁功率装置的数学模型。

同步发电机和励磁功率装置的数学模型可表示为[5]：

(1)

(2)

(3)

(4)

(5)

(6)

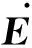
分析上述模型可知，同步发电机模型含有一定的不确定性，具体来源于两个方面： ① 该模型是通过线性化得到的，引入了一定的不确定性；② 该模型中的参数存在一定的误差，导致模型具有不确定性。

3 励磁系统自动调节器设计

针对上述数学模型，笔者设计如图1所示的励磁系统，并设计相应的自动调节器。测量装置包括变压器、桥式整流电路和阻容滤波器等。变压器可视为比例环节，其比例因子是变压器的变比。整流电路同样可视为比例环节。阻容滤波器通常是一个惯性环节。晶闸管整流装置可视为一组按一定时间间隔轮流工作的开关，其工作周期由整流电路的形式决定。晶闸管元件触发导通相比输入信号的变化有一个纯延时，延时的长短由整流电路的形式决定。为简化设计，可将晶闸管整流装置视为惯性环节。

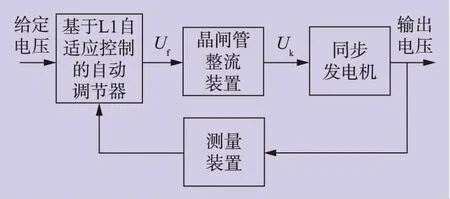
图1 励磁系统设计原理

结合数学模型，采用基于L1自适应控制的方法，进行励磁系统自动调节器的设计。按照文献[4]中给出的方法，反馈增益矩阵K和低通滤波环节D(s)的设计需要反复手动调试，考虑到问题的非凸特性，可以采用智能优化算法求解。为克服缺点，笔者提出一种基于支持向量机与遗传算法的K和D(s) 优化算法。限于篇幅，遗传算法和支持向量机的具体原理不再赘述。在此，给出具体的自适应控制器优化设计算法，步骤如下。

(1) 根据系统输出的维数，选定增益矩阵K和D(s)的阶次。例如，假定系统的输出变量为m维，则K和D(s)为m×m矩阵。此处输出为1维，也即m=1，因此K和D(s)均为1维矩阵。

(2) 设定K的各个元素为待优化的常数Kij，设定D(s)的各项元素为待优化的传递函数，其形式为Dij/s(i,j=1,2,…,m)，Dij是待优化常数。将所有的待优化变量组合，构成未知向量X=[K11,K12,…,Kij,…,Kmm,D11,D12,…,Dij,…,Dmm]T

(3) 选择合适的编码方案，将待优化变量X转换为染色体，也即根据适当的规则，将其编码为字符串。

(4) 选择合适的遗传算法参数，包括种群大小M与交叉概率Pc等。

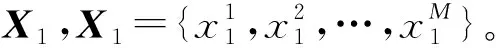
(6) 对种群中的个体逐个进行译码，得到未知变量X的具体取值，逐个计算得到矩阵Ci(s)：

(7)

式中：Di(s)为第i个个体对应的D(s)矩阵；ω为频率；Ki为第i个个体对应的增益矩阵；Im为m×m单位矩阵。

(7) 结合矩阵Ci(s)和系统模型，计算加入L1自适应控制器后系统的回路传递函数Lo(s)：

(8)

Hm(s)=C(sI-A)-1B2

(9)

计算该传递函数的结构奇异值σ[Lo(s)]，结构奇异值定义参见文献[6]，I为4×2单位矩阵。

(8) 计算加入结构奇异值约束后每个个体的适应度函数fi及种群的总适应度F。

(9) 基于得到的适应度函数，根据一定的算法，对种群进行选择、交叉与变异操作。

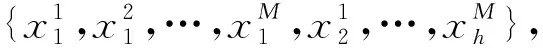
(11) 由设计者指定适应度阈值f*，根据适应度值的大小，对个体序列中的个体进行分类。将适应度大于f*的个体归入集合M，其余归入集合N。

(12) 构造集合M到集合{1}的映射，以及集合N到{-1}的映射。

(13) 将集合M中的元素进一步划分至子集合M1和M2，集合N中的元素进一步划分至子集合N1和N2。取M1与N1构成新集合S1，取M2与N2构成新集合S2。令S1为训练集，S2为测试集。

(14) 选取适当的参数，对训练集S1中的样本x应用支持向量机方法进行分类，得到决策函数：

(10)

式中：xi为第i个样本；l为样本总数；yi为第i个样本对应的输出；k(xi,x)为核函数；αi与b为可通过优化方法得到的参数。

(15) 应用集合S2对上述决策函数进行测试，若满足分类的错误率要求，则可以确定该函数为个体分类的超平面。

(16) 根据一定的算法，对步骤(10)中所得种群中的个体进行选择、交叉与变异操作。采用步骤(14)中的决策函数对种群中的个体进行分类，对于决策函数值大于0的个体，重新执行步骤(6)～(8)，计算其适应度函数，并判断适应度函数值是否满足优化计算的终止条件。若满足，则输出Ci(s)的优化结果，转入步骤(17)。否则，继续重复步骤(6)～(8)。

(17) 将Ci(s)结果代入系统模型，进行相应的时域阶跃信号仿真分析。如所得结果满足系统指标要求，则认为得到了优化结果，运算停止。否则，更改D(s)中元素的形式为Dij/s2(i,j=1,2,…,m)，转入步骤(2)。

上述算法确保所得的Ci(s)满足设计条件，使系统回路传递函数矩阵的结构奇异值在一定范围内，同时使‖1-Ci(s)Hm(s)‖L1最小，保证了系统的鲁棒性。

4 仿真分析

对采用前述方法设计的同步发电机励磁系统自动调节器进行数学仿真分析，模型参数选择参见文献[7-8]。图2～图3分别给出了闭环系统在载荷突然增大和减小情况下的动态特性曲线，包括电压U、电流I、功率P、励磁电压Efd的变化情况，图中的变量均为标幺值[9]。

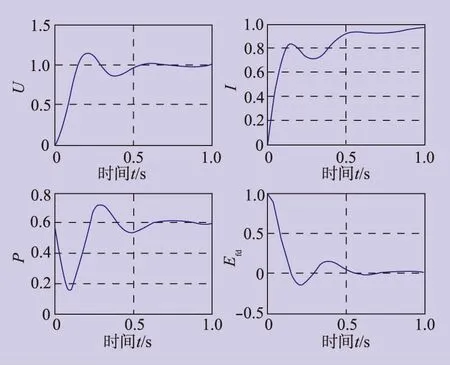
图2 载荷突然增大时动态响应曲线

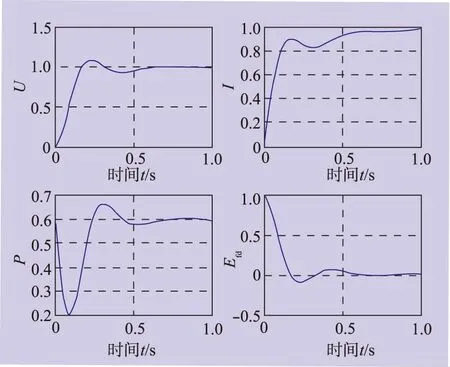
图3 载荷突然减小时动态响应曲线

从仿真结果可以看到，在静态载荷突然增大或者减小50%时，由于L1自适应控制器的作用，电压经过振荡后很快恢复到给定值。进一步分析参数摄动对系统仿真结果的影响，令系统标称状态方程中的因数发生摄动，包括正向摄动20%和负向摄动20%[10]。从仿真结果可以看出，当静态载荷突然增大时，在第一种摄动情况下，输出电压的振荡略有加剧，但幅值和稳定时间基本不变；在第二种摄动情况下，输出电压的振荡略有减缓，幅值不变，稳定时间有所缩短。当动态载荷突然增大时，第一种摄动电压的振荡有所加剧，但其余指标基本不变；在第二种摄动范围内，系统的动态电压变化率为5.05%，稳定时间为0.1s。可见，笔者提出的方法可以有效实现参数摄动情况下的电压自动调节，从而说明这一方法是有效的。

5 结论

针对同步发电机的励磁系统，根据发电机工作环境干扰和负载波动，设计了基于L1自适应控制的同步发电机励磁系统自动调节器。建立了同步

发电机和励磁系统功率装置的数学模型，为自动调节器的设计奠定了基础。提出一类多输入多输出线性系统的L1自适应控制方法，并基于该方法设计了自动调节器。仿真结果表明，采用这一方法设计的自动调节器在负载存在波动及外部干扰的情况下，可以实现同步发电机电压的稳定控制，具有较高的工程应用价值。

[1] 孙郁松,孙元章，卢强，等.水轮机调节系统非线性H∞控制规律的研究[J].中国电机工程学报,2001，21(2)： 56-59.

[2] 董清,高曙，鲍海.同步发电机调速系统附加H∞鲁棒分散控制[J].中国电机工程学报,2002，22(2)： 47-51.

[3] 赵闻飚,施颂椒，郭尚来.水轮发电机组H∞状态反馈综合最优控制系统[J].上海交通大学学报,1996，30(4)： 126-131.

[4] HOVAKIMYAN N, CAO C Y.L1Adaptive Control Theory： Guaranteed Robustness with Fast Adaptation[M]. Philadelphia： Society for Industrial and Applied Mathematics, 2010.

[5] 黄曼磊,李殿璞,唐嘉亨.船舶电站柴油机调速系统H∞控制器的设计[J].中国造船,2001,42(4)： 46-51.

[6] 杨承恩,贾欣乐.舵阻摇H∞控制器的设计[J].中国造船,1999,40(1)： 37-45.

[7] 张汝均.船舶电站同步发电机的自动励磁装置[M].北京： 国防工业出版社,1989.

[8] 赵涵，张晗，和磊，等.基于DSPf28335的数字式励磁控制系统设计[J].计算机与数字工程,2016,44(5)： 971-974.

[9] 武哲龙.三代核电励磁调节器设计优化与研究[J].中国高新科技，2017,1(7)： 30-32.

[10] 任雪峰.基于现代优化算法的电厂励磁改造的研究[D].武汉： 湖北工业大学,2017.