大型水轮发电机空载电压波形及谐波分析方法研究

王 韬，李金香，张春莉

(1． 水力发电设备国家重点实验室，黑龙江哈尔滨 150040；2． 哈尔滨电机厂有限责任公司，黑龙江哈尔滨 150040)

0 引言

在大型水轮发电机中，由于凸极同步电机的凸极效应，定转子间的偏小气隙以及每极每相槽数较少等原因，造成了发电机的空载电压中往往包含高次谐波。这就需要设计人员合理的设计，避免高次谐波影响电压波形，从而保证电能的质量。

空载线电压全谐波畸变因数(THD)是水轮发电机的重要性能指标，它直接反映了电压波形的正弦性和谐波情况。谐波不仅会在电机中产生损耗、影响效率，还会在用电设备上产生附加损耗，使其效率降低及对临近的通讯设备产生干扰。国家标准GB/T 7894《水轮发电机基本技术条件》和GB/T 1029《同步电机试验方法》中对空载线电压全谐波畸变因数(谐波次数为100次)进行了说明并明确了限值不大于5%，空载线电压电话谐波因数(谐波次数为100次)限值不大于1.5%。

对于空载电压波形的研究，开始一直是采用解析法进行计算[1]，这种方法从机理上解释了对空载电压波形的影响因素，但是对于阻尼条涡流效应以及偏心磁极和定子斜槽等因素是比较难考虑的。基于这种情况，有限单元法的提出和应用[2]可以很好的应对以上的困难，但是对于转子旋转的问题较难解决。

因此，场路耦合方法就可以很好的克服转子旋转的问题。对于转子旋转的运动媒质问题，运用滑动表面和运动带宽的技术来应对气隙的剖分，利用运动有限元方法来求解问题[3]。

在前人的工作基础上，本文采用的是二维场路耦合法对电机进行计算并分析。建立的假设和约定条件如下：

1) 假设发电机电磁场为似稳场，不计位移电流的影响；

2) 发电机磁场沿轴向不变，将发电机三维电磁场简化作二维平行平面场处理；

3) 发电机定子铁心外部没有漏磁，转轴为非磁性材料；

4) 发电机转子以恒定同步转速ns旋转。

1 数学模型的建立

根据Maxwell基本方程组，一般电机内时变电磁场的变化规律可用下式表达：

(1)

式中：H为磁场强度；B为磁感应强度；E为电场强度；D为电位移矢量；J为电流密度；ρ为电荷密度。

对于各向同性的媒质，媒质成分方程为：

(2)

式中：ε为媒质介电常数；μ为媒质导磁系数；σ为媒质导电系数；E(e)为局外力所产生的电场强度；对不存在局外电场强度的区域，E(e)=0。

根据前文假设忽略位移电流，即：

(3)

因此Maxwell方程组可以简化为：

(4)

引入矢量磁位A，令：

(5)

于是可得到：

(6)

对于空间直角坐标系，可将以上各矢量都分解为x、y、z轴三个方向的分量，那么上式的矢量方程可分解为如下三个标量方程式的形式：

(7)

根据前文假设磁场沿轴向不变，将电机作为二维平面场来进行处理，因此矢量电密J与矢量磁位A都只存在z轴分量，即：

(8)

于是式(7)可变为：

(9)

上式就是发电机二维电磁场矢量磁位方程的一般形式，它是发电机二维电磁场分析的基本方程。

当水轮发电机的转子与定子有相对运动且励磁绕组通电时，则电机内还会产生与矢量速度v有关的电场Ev：

(10)

于是在求解电机运动时变电磁场时，计算区域内的电密矢量可表示为：

(11)

式中：Js=σE(e)为外施矢量电流密度。此时的矢量磁位A既是时间的函数又是空间的函数，即A=A(t，x，y，z)。

在二维平面场的条件下：

(12)

由于此时v没有z轴分量，A没有x、y轴分量，于是上式可变为：

(13)

将上式代入式(9)中即可得到二维时变运动电磁场的基本方程：

(14)

2 场路耦合模型的建立

采用线性三角单元剖分，忽略有源电流区域内的涡流，式(14)可离散为：

Q·pA+K·A=C·Ib

(15)

式中：p为微分算子；A为节点向量磁位矢量；Ib为电流矢量；Q、K为系数矩阵；C为线圈电流与单元节点的关联矩阵。

电机为全阻尼结构，假设一个单元电机内有n根阻尼条，每相邻两根阻尼条构成一个阻尼绕组回路。则电机内各回路的电压方程为：

U=pΨ-R·I

(16)

式中：U为电压矩阵；I为电流矩阵；R为电阻矩阵；Ψ为磁链矩阵。

由于上式的二维电磁场基本方程只能针对电机铁心直线部分的电磁场进行计算，无法计及电机端部的影响。因此在本文的场路耦合数学模型中，将回路磁链分成铁心直线部分磁链与端部漏磁链两部分，即：

Ψ=Ψm+Ψe

(17)

端部漏磁链：

Ψe=Le·I

(18)

端部漏感矩阵：

(19)

式中：Lse为定子回路端部漏感矩阵；Lfe为励磁绕组的端部漏感；LDe为阻尼绕组回路的端部电感矩阵。

铁心直线段磁链可由求解二维时变有限元的方法获得：

Ψm=lefG·A

(20)

式中：lef为电机铁心轴向有效长度；G为系数矩阵。据此，电机内回路电压方程可变为：

U=lefG·DA+D(Le·I)-R·I

(21)

至此，我们得到了二维场路耦合求解的全部理论研究方法。

3 计算实例

本文以一台大型水轮发电机为对象，对空载电压波形进行研究，该发电机参数如表1所示。

表1 发电机基本数据

该水轮发电机每极每相槽数为9/4，图1所示为一个单元电机的求解区域。

图1 求解区域及网格剖分

图2为网格的局部剖分，深色带为运动带宽剖分技术，运动带上表面即为滑动表面。

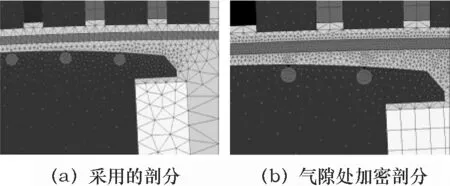
图2 网格剖分的局部放大与运动剖分带处理

由于在计算时定、转子之间是存在相对运动的。如果剖分不当，将会在定、转子相对运动时网格发生变化，导致求解计算发生变化。对于定、转子间气隙带的剖分，本文采用了分层剖分技术，将定、转子间的气隙带分为上中下三层。上层为定子层，认为其不旋转；中间层为运动带宽，是随转子运动而旋转的；下层为转子表面层，亦随转子的运动而旋转，其难度在于阻尼条槽口和极靴表面组成的不连续面，为了得到质量好的剖分，运用了多段剖分技术，保证了精确性。

中间层剖分的好坏将会直接影响求解的结果，故此将此运动带的上下表面做成等距剖分，如图2(a)所示。为了判断上下表面等距剖分是否合理，在图2(b)中对气隙部分进行了分层加密，同时对两种情况的齿槽转矩进行了分析。通过分析两种情况下的齿槽转矩发现，两种剖分下，发电机的齿槽转矩在一个周期内基本相当。剖分加密后使得单元增多，会让求解计算时间变长，而计算精度的收益却很小，故此运动带上下等距剖分是一种较为理想的剖分方式，在较短的求解时间内得到精确的求解结果。

图3为该水轮发电机耦合的电路模型，Q1为阻尼绕组；BA-Plus、BB-Plus和BC-Plus分别表示与有限元部分耦合的A、B、C相定子绕组；BA-Minus、BB-Minus和BC-Minus分别表示与有限元部分耦合的X、Y、Z相定子绕组电阻。RAB、RBC和RCA为开路测量电阻。

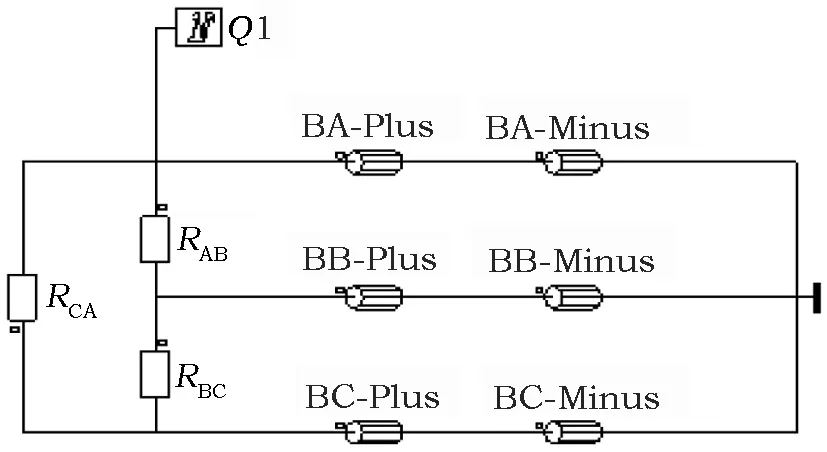
图3 耦合电路

利用Newton-Raphson迭代方法来求解非线性时变方程组，并同时用时步迭代求解各个时刻的磁场分布。由于发电机的每极每相槽数为9/4，为了在谐波分析中考虑到各阶齿谐波， 故此每个周期分析到100次谐波，迭代时步长取0.000 04 s，仿真时间为0.04 s即2个周期，得到该水轮发电机的空载磁场分布和磁密云图分布如图4所示。

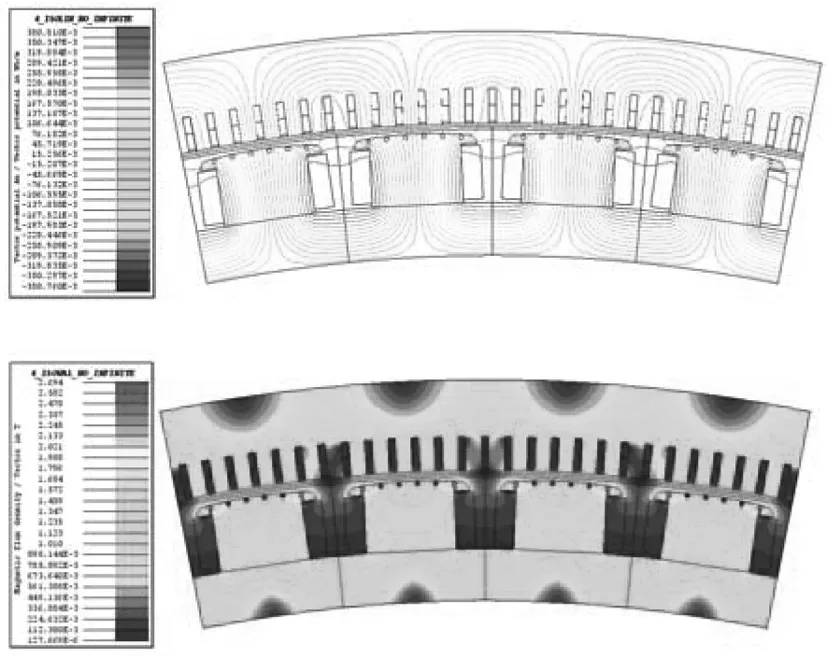
图4 空载磁场分布和磁密分布云图

从图5中可以看出，在空载运行时，阻尼条中是有涡流存在的，并且每根阻尼条的电流幅值并不相同。这一点是与之前通过解析法计算空载磁场不同的，即在计算中考虑了阻尼条的涡流对气隙磁场的影响，并没有将其忽略。

空载磁场的气隙磁密和空载电压波形如图6所示，对空载电压波形进行傅里叶分析，得到频域中的频谱图如图7所示，并且对基波及谐波进行分析。

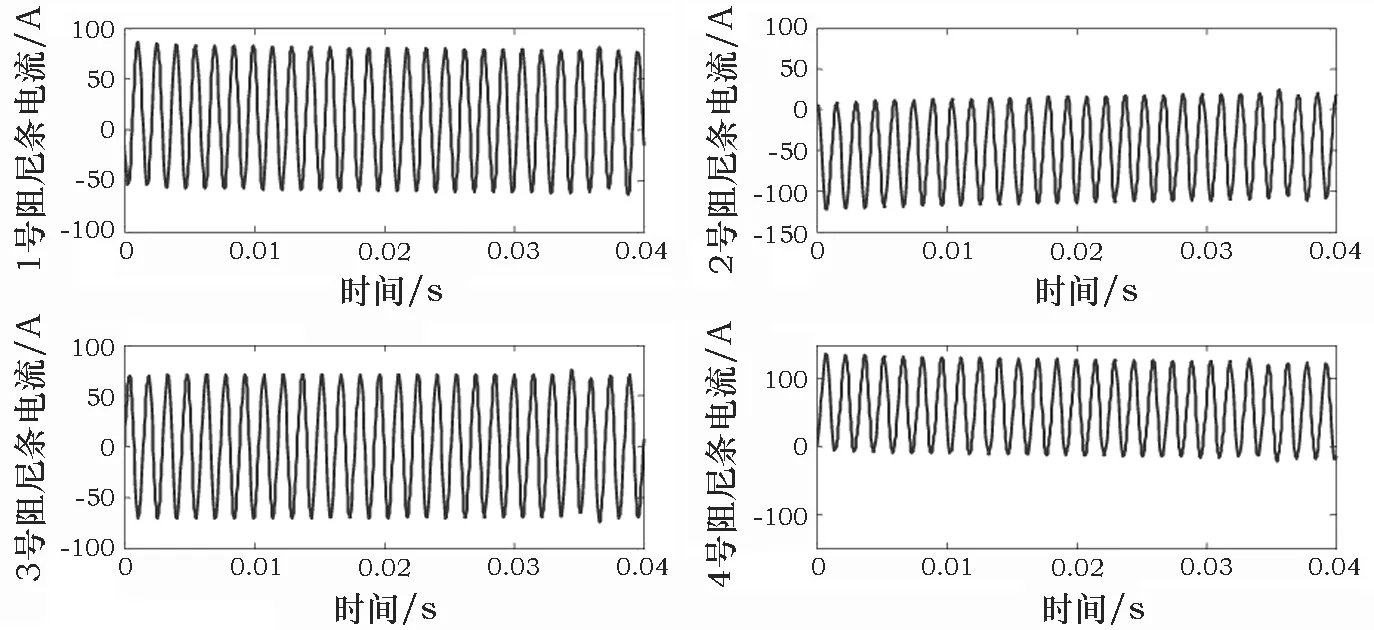
图5 某磁极阻尼条电流

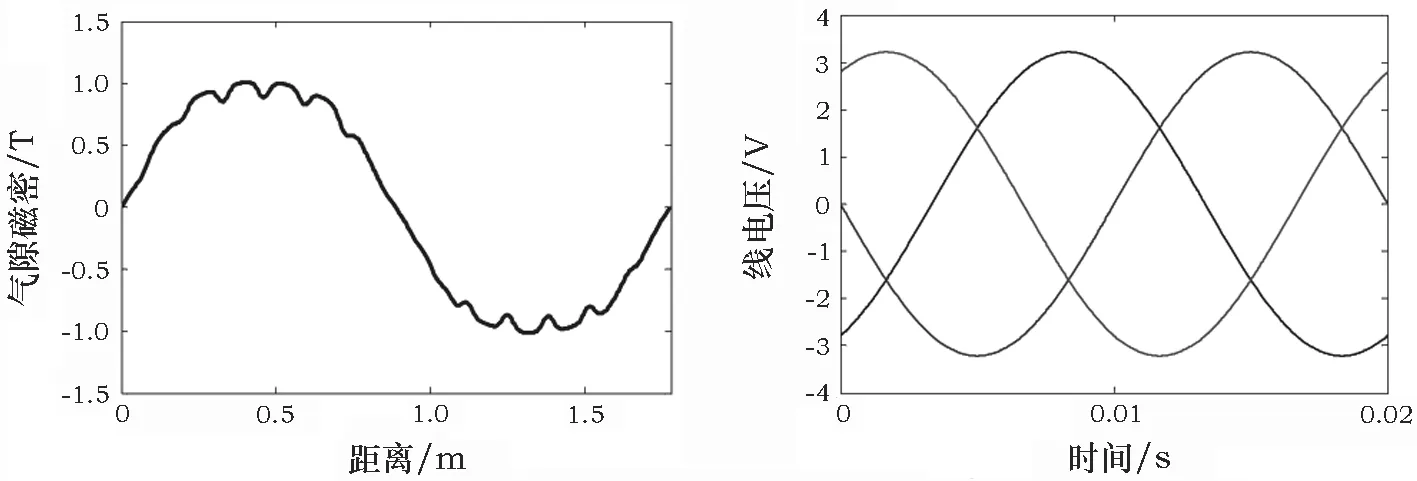
图6 气隙磁密和空载电压波形

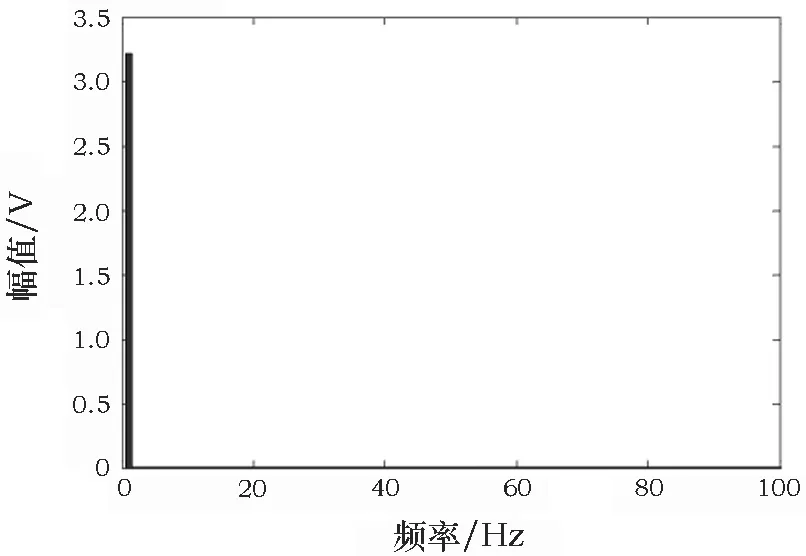
图7 线电压波形傅里叶分析

根据空载线电压全谐波畸变因数(THD)的定义及标准GB/T 1029《三相同步电机试验方法》给出的计算方法，THD如下所示：

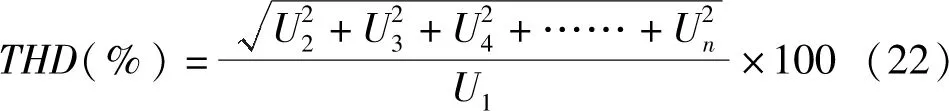
式中：U为线电压的有效值；Un为第n次谐波电压的有效值。

根据式(22)得到该水轮发电机空载线电压全谐波畸变因数(THD)为0.147%，满足标准。

本文分析的水轮发电机为分数槽绕组，本身这种绕组形式对高次谐波就会有一定的削弱作用，将会使得空载线电压波形的正弦性比较好。对于整数槽绕组发电机来说，由于空载波形的正弦性相对较差，可以通过调整阻尼条节距与定子齿距的比例或阻尼条进行偏转等方式来削弱空载电压波形中的高次谐波。此外还可以通过定子斜槽的方式来削弱高次谐波图8、图9为定子斜槽结构的空载磁场分布及空载电压的波形对比。由图可知电压波形有了明显改善。

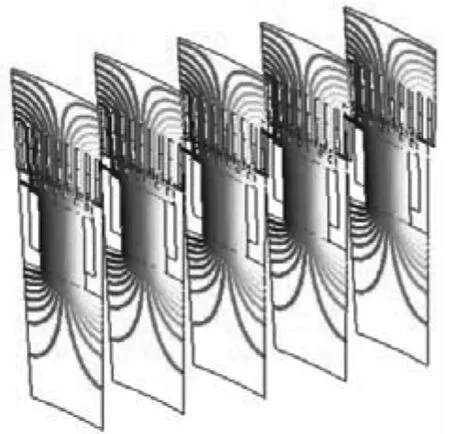
图8 定子做斜槽后空载磁场分布

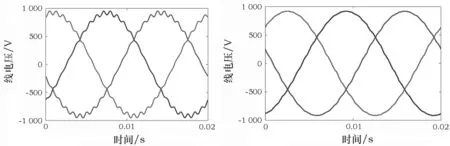
a) 定子斜槽前 b) 定子斜槽后图9 定子斜槽前后空载电压波形对比

4 结论

相对于传统解析法而言，本文所采用的二维时变场路耦合法分析，可以考虑定转子间的运动，并很好的考虑了转子阻尼条的影响，更为精确。

对电压波形的分析可以很好预测和指导大型水轮发电机的设计，使其高次谐波进行削弱，从而提高整个电网的电能质量。

[1] 李哲生.改善凸极同步发电机空载电势波形的措施[J].哈尔滨电工学院学报，1983，6(3)：1-16.

[2] 李槐树，李朗如，让余奇.阻尼绕组对凸极同步发电机空载电势波形的影响[J].电机与控制学报，2003，7(4)：267-271.

[3] 周光厚，张天鹏.大型水轮发电机空载电压波形及谐波的有限元计算[J].东方电气评论，2008，86(22)：32-37.