基于小波神经网络的交通状态短时预测

曹渝

（广州杰赛通信规划设计院有限公司，广东 广州 510310）

1 引言

交通状态短时预测是指基于动态获取的道路交通参数-道路状态数据的时间序列推测未来短时间段的交通流状态[1]。交通预测技术基于先进的交通状态监测手段，通过实时提取现有交通道路的交通参数，结合具有实时性的预测模型，实现未来时间段交通道路的短时预测。交通状态的预测研究已经有不少的理论和方法，既有根据规则进行相关统计分析的预测模型，也有采用人工智能技术的智能分析方法。

典型的统计分析模型有：孙晓亮[2]采用熵的方法实现短时交通状态的预测；王新颖[3]利用非参数回归模型实现交通状态的回归预测；郑建湖[4]则采用马尔科夫链，结合车辆的初始交通状态、转移概率以及下一时刻车辆的交通状态构建短时交通状态预测模型。

人工智能分析模型有：盛春阳[5]等人采用贝叶斯网络计算交通参数之间的条件概率来预测各种交通状态发生的概率；钱民[6]采用定性动态概率网络构建的交通状态预测模型，计算各路口发生拥堵的可能性；陶丽[7]利用改进小波神经网络模型实现交通状态的预测。

统计的分析方法相对简单，却无法反映动态的交通状态变化的特征；人工智能分析的方法具有学习特征，能够反映动态的交通状态变化的特点，但是其需要庞大的训练库以保证算法的精度。考虑到现在多种终端数据融合遇到的各种困难，本文采用通信移动用户的数据作为交通参数提取的数据源，通过分析移动用户的出行特征提取其实时的交通参数，然后再利用小波神经网络的方法构建交通状态预测模型，实现交通状态的短时预测。

2 小波神经网络的相关研究

2.1 小波分析

小波分析克服了傅里叶处理非平稳信号的缺陷，它不仅能够获取一段信号包含的频率成分，还能采用有限长的会衰减的小波基构建灵活可变的时间-频率窗，实现了信号的时频分析，也就是信号在各个时刻的瞬时频率及其幅值[8]。

小波分析的基本思想是伸缩和平移。其公式为：

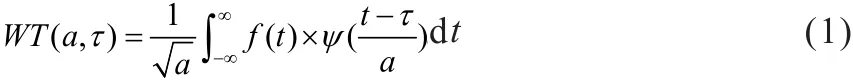
其中，尺度a控制小波函数的伸缩，平移量τ控制小波函数的平移。尺度对应于频率，而平移量对应于时间。

小波分析作为一种新的时频信息方法，它可以采用小波基，将不同频率和尺度的信号通过不同的伸缩和平移分离出来，因此可高效分离不同类型的信号，且在信息转换的过程中无信息的损失和扭曲。

2.2 前馈型神经网络

前馈型神经网络用于处理复杂的非线性分类情况。复杂的非线性分类会出现组合爆炸式高阶输入，而前馈式神经网络采用参数矩阵确定方法对样本进行预测，得出样本的分类结果。

前馈神经网络是一种单向神经网络，各神经元从输入层开始，接收上一级输入，并输出至下一级，直到输出层。同一层的神经元之间没有任何联系，层间信息的传递只沿一个方向进行。因此，前馈式神经网络的前馈仅仅用于计算网络的输出，并不对网络的参数矩阵进行调整。

典型的前馈神经网络是BP神经网络，BP神经网络又称为连接权调整采用反向传播学习算法的前馈神经网络。其权值和阈值的调整恰恰是通过误差反向计算方式实现的。在模型的训练阶段，采用多层网络的方法计算出整个样本数据的总误差，然后从输出层网向前推，一般采用梯度下降法逐层求出每一层神经元的阈值和权值的调整量，循环迭代，当网络参数满足算法设定的要求则停止运算。

图1直观展示了典型的三层神经网络模型向前传播的例子。左边的Layer L1代表网络的输入层，“+1”表示输入层的偏置节点，第二层Layer L2代表网络的隐含层，第三层Layer L3代表网络的输出层。

最典型的神经网络是BP神经网络，其输入输出的

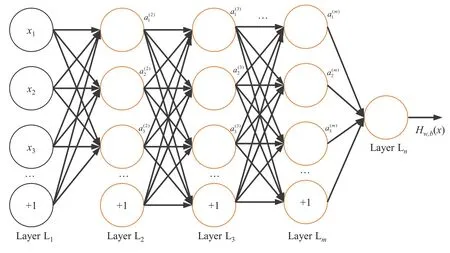
图1 典型的神经网络模型

映射关系为：

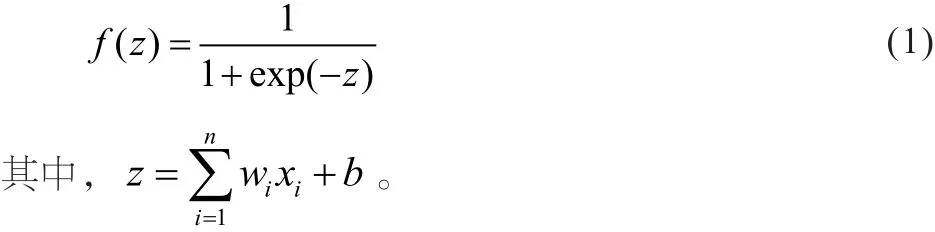
反向计算的本质是根据输出层与实际结果的总误差，通过隐含层的神经元调整神经网络权值和阈值。因此反向计算的算法流程：

（1）进行前馈传播计算，利用前向传播公式，得到各Layer L2，Layer L3，…，Layer Ln（输出层）的激活值。

为了简化模型，以下仅介绍具有一层隐含层的前向传播计算方式。隐含层中n个神经元的表达式为：

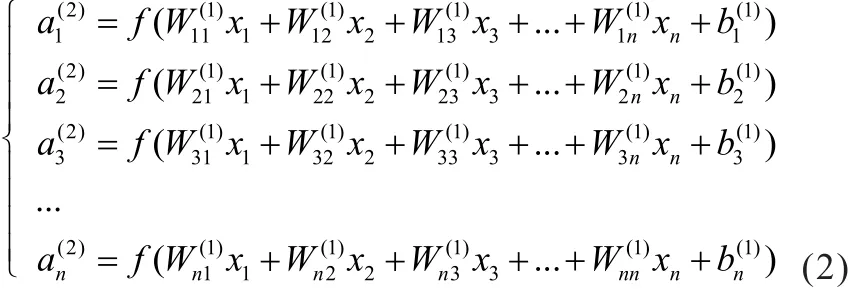
输出层的神经元表达式为：

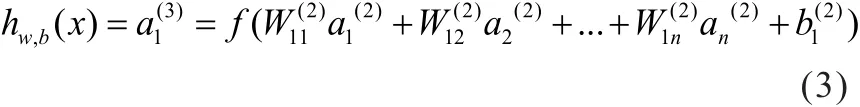
那么，如果存在多层隐含层的神经网络，前馈传播的步骤为：

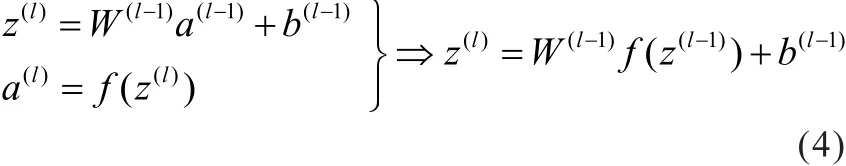
（2）设定目标函数，给定一个包含样本的训练集，目标函数为：

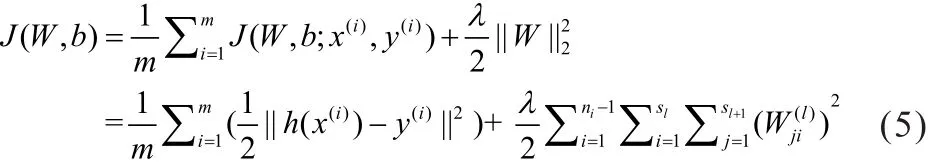
（3）采用梯度下降方法最小化J(W,b)，参数更新方式为：

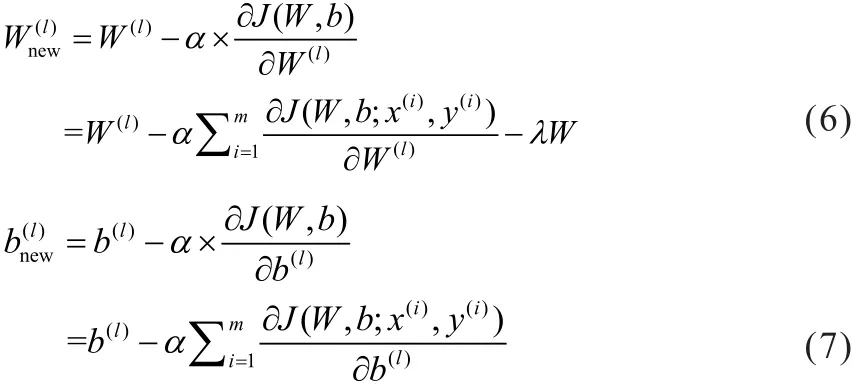
反向计算的权值和阈值更新关键在于

根据链式法则可得：

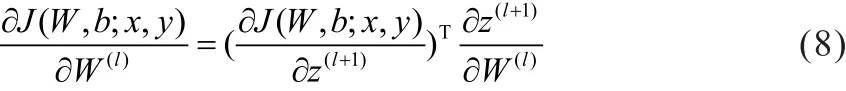
其中，

定义残差为：

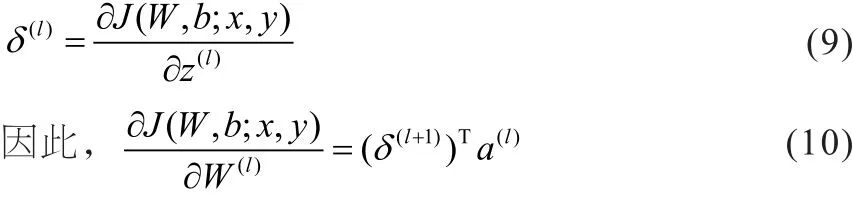
同理：

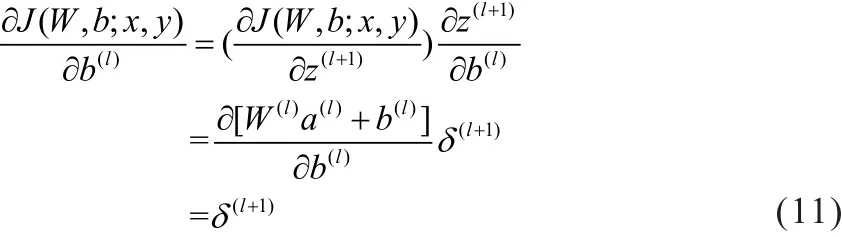
（4）经过权值和阈值的更新，得到的输出层与实际结果的总误差小于设定的条件，则停止计算，否则，继续返回第二步进行参数更新，直到满足条件为止。

2.3 小波神经网络

通过上述的分析可知，BP网络的误差空间是一个形状极为复杂的N维曲面，该曲面上的每个点的“高度”对应于神经网络的总误差，每个点的坐标向量对应着N个神经元的权值。图2为一个神经网络二维误差空间的示意图，从图2可知，当权值在误差空间的平坦区域时，误差下降缓慢，影响收敛速度。除此以外，由于引进了sigmoid函数，误差对权值的梯度变化小（接近于零），这种情况使得训练经常陷入某个局部极小点，从而使训练无法收敛于给定误差。

针对上述神经网络存在的缺点，采用小波基函数取代sigmoid函数来优化网络参数和误差空间，这种以小波基作为模式识别的特征函数，采用小波基以及输入向量的内积进行加权实现输入层的特征提取，结合了小波特有的时频局域化的特征以及神经网络的自学习功能，实现了具有较强的非线性拟合能力和较好的收敛速度。

因此，小波神经网络的输入-输出映射可以表现为：

3.2 移动用户出行数据的采集和分析

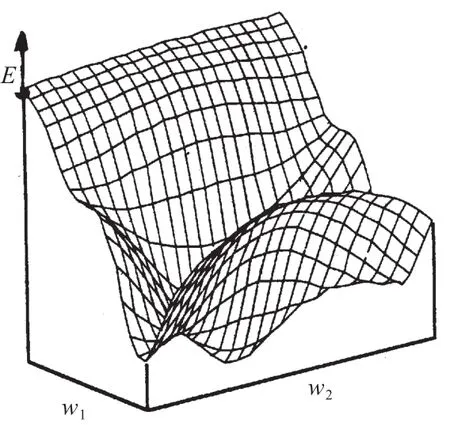
图2 神经网络二维误差空间

其中，ψ（.）为函数的母小波基函数，尺度ai控制小波函数的伸缩，平移量bi控制小波函数的平移，wi是网络神经元的连接权值，N为母小波的数目。

本文采用保定某运营商提供的2015年3月1日至2015年12月30日移动用户的通话和流量详单数据，该数据大小为300 G，包含50多万用户发生业务的位置切换及位置更新的相关信息，选择实验范围为主城区某一条主干道总长15 km的道路。

首先，根据移动用户发生业务的通信信号特征，把移动用户的轨迹定位到10 m×10 m的网格中；然后根据出行数据的时间戳算出移动用户在一段位移中的速度和加速度。由于移动通信的信号有不稳定的特点，很可能刚切换过来的基站的信号又变弱，手机又开始往回切换，从而造成“乒乓效应”。这两个值相差越大，“乒乓效应”发生的可能性就越小。但太大又可能造成手机在合适的时候无法使用下一基站通话。因此，针对移动用户的出行数据，本文需要对“兵乓切换”的数据进行剔除。

移动用户的位置数据、速度数据以及加速度数据如表1所示。

针对表1采集的速度、加速度数据，把疑似发生“兵乓切换”效应的数据进行剔除。如：该用户在起始时间为201501082153发生的速度为41.6 m/s，相当于150 km/h，该速度已经超过主干道的合理速度，因此需要剔除该类异常数据。

3 基于小波神经网络的交通状态短时预测

3.1 交通状态短时预测的基本流程

基于交通流数据的短时预测就是充分借助各种交通流采集设备提供的源数据，采用相关的模型，从源数据中发现各种交通状态发生的规律。因此，要实现交通状态预测，首先需要对采集到的数据进行预处理，并提取能够反映交通流特征的交通参数；然后选用合适的模型，在模型中输入预测的样本数据，预测下一个时间段的交通状态。交通状态预测的基本流程如图3所示：

3.3 采用小波神经网络预测交通状态

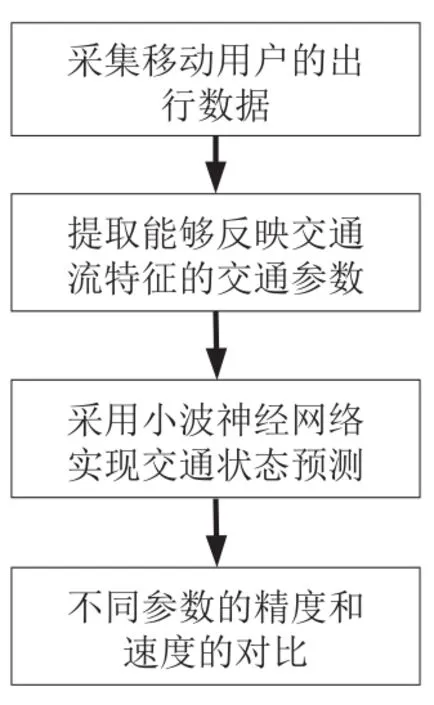
图3 交通状态预测的基本流程

本文选取交通流的参数-速度和加速度作为输出对象，交通状态（拥堵、拥挤、轻度拥挤、畅通）为预测对象。随机抽取移动用户出行样本1 872个作为训练样本，剩下1 873个作为预测检验样本。本文分别采用小波神经网络和BP神经网络两个模型进行实验，模型的相关参数如表2所示：

表2 小波神经网络和BP神经网络模型的参数

3.4 小波神经网络模型的仿真实验

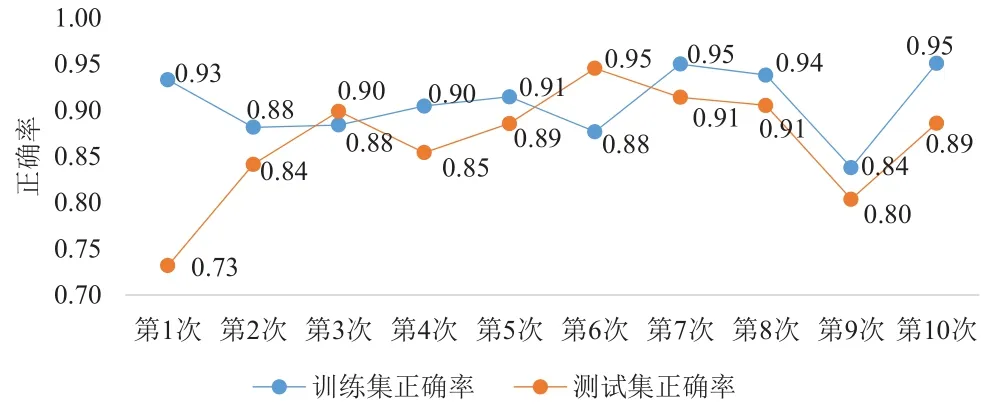
本次实验采用matlab工具进行仿真，第一次实验采用学习速率（又称为修正权值的学习速率）为0.07，隐形节点和迭代次数可参照表2，本文随机抽取训练数据10遍，小波神经网络训练和预测的总时间平均为107 s；BP神经网络训练和预测的总时间平均为178 s，均满足交通状态5分钟更新一次的要求。每一遍的训练集和测试集的正确率如图4、图5所示：

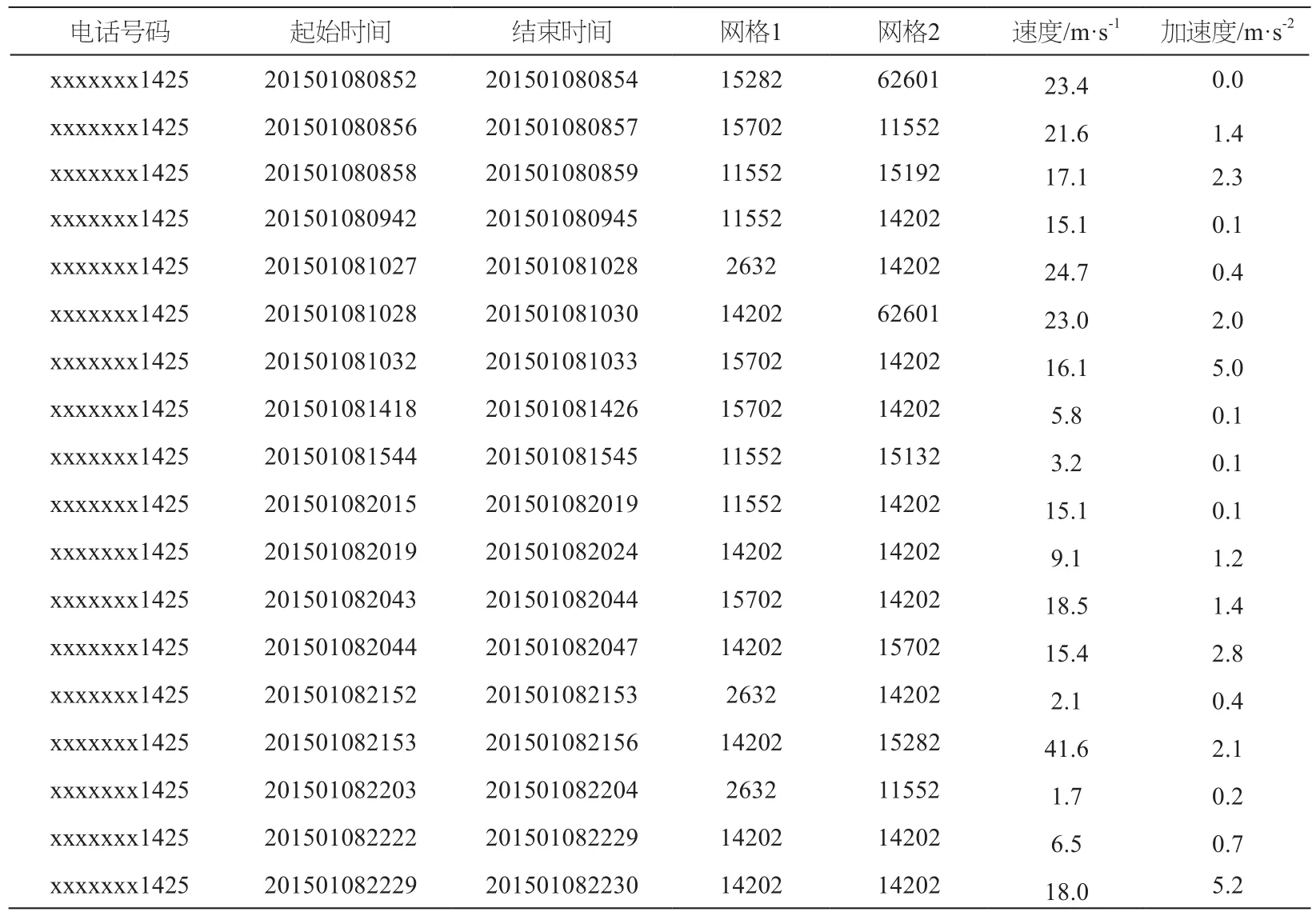
表1 移动用户出行数据的采集和交通参数提取

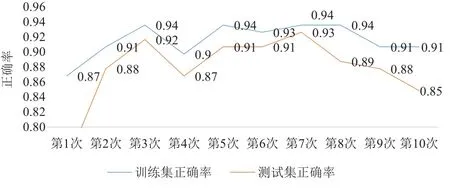
图4 小波神经网络实验仿真结果的准确率示意图（学习速率0.07）

第二次实验采用学习速率是第一次的10倍，为0.7，隐含层节点和迭代次数与第一次的一致，同样抽取训练数据10次，小波神经网络训练和预测的总时间约为38 s，BP神经网络训练和预测的总时间约为46 s，小波神经网络实验时间基本满足5分钟更新一次的要求。其训练集和测试集的正确率如图6、图7所示：

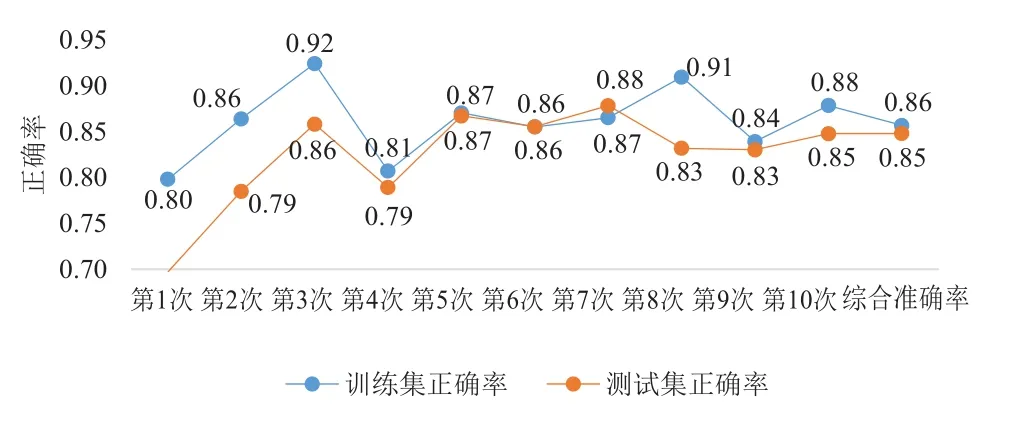
图5 BP神经网络实验仿真结果的准确率示意图（学习速率0.07）

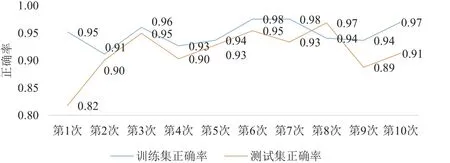
图6 小波神经网络实验仿真结果的准确率示意图（学习速率0.7）

通过本实验的仿真可知，在最大迭代次数设定的情况下，无论是神经网络还是BP神经网络，学习速率跟收敛时间成反比，与精度成正比，反之亦然。该实验更能够说明，如果循环次数设定，学习速率过小，神经网络sigmoid函数在计算的过程误差对权值的梯度变化小，容易陷入某个局部极小点使得拟合能力降低。

本文通过对比得知，在参数一致情况下，小波神经网络无论在非线性拟合能力还是在收敛速度上都优于BP神经网络。因此，小波神经网络在预测交通状态的性能以及拓展性比传统的BP神经网络更佳。

4 结束语

本文利用移动用户的出行数据提取交通参数，分别采用小波神经网络和BP神经网络进行交通状态的预测。实验表明，在参数一致的情况下，小波神经网络采用小波基取代sigmoid函数来优化神经网络具有较强的非线性拟合能力和较好的收敛速度，而且随着数据量的扩展，小波神经网络具有更大扩展性的优势。智能交通系统拥有海量的交通参数，可借助小波神经网络进行交通状态的短时预测，以实现整个城市范围的交通状态的短时预测。

[1] Fangce Guo, Polak J W. Comparison of modeling approaches for short term traffic prediction under normal and abnormal condition[C]//13th Intelligent Transportation Systems(ITSC) International IEEE Conference 2010. IEEE, 2010: 1209-1214.

[2] 孙晓亮. 面向城市快速路的道路交通状态预测方法的研究[D]. 北京: 北京交通大学, 2009.

[3] 王新颖. 基于网格的短时交通状态预测研究[D]. 长春:吉林大学, 2010.

[4] 郑建湖,林小惠,郑礼席,等. 基于马尔可夫链模型的交通拥挤状态预测[J]. 交通标准化, 2012(22): 76-79.

[5] 盛春阳,张元. 基于贝叶斯网络模型的交通状态预测[J].公路与汽运, 2008(1): 29-31.

[6] 钱民,唐克生. 基于定性动态概率网络的交通状态预测及改进[J]. 云南大学学报: 自然科学版, 2012,34(2):165-168.

[7] 陶丽. 基于改进小波神经网络模型的交通流预测研究[D]. 上海: 上海工程技术大学, 2015.

[8] 章文俊. 小波神经网络算法及其船舶运动控制应用研究[D]. 大连: 大连海事大学, 2014.

[9] 赵娜,袁家斌,徐晗. 智能交通系统综述[J]. 计算机科学,2014,41(11): 7-11.

[10] 吴忠金. 基于车联网的城市道路交通状态识别算法研究[D]. 广州: 华南理工大学, 2012. ★