战斗部轴向威力的增强*

谭 振，陈鹏万，周 强，祝 奎，刘文斌

(北京理工大学爆炸科学与技术国家重点实验室，北京 100081)

杀伤战斗部是打击人员及具有轻型防护能力目标的常用战斗部。杀伤弹爆炸后，弹体内部装药爆炸驱动壳体向外快速膨胀，膨胀到一定限度后，壳体表面开始出现裂纹，裂纹相互贯通使壳体全部破裂形成破片并以一定初速向四周飞散以杀伤目标。

弹体爆炸形成的破片可分为自然破片、可控破片、预制破片。由于自然破片战斗部爆炸后形成的破片数量少、形状不规则、质量分布不均匀、飞行阻力大、速度衰减快，所以常规杀伤战斗部大都采用轴向或周向均布预制破片结构，以改善杀伤战斗部的杀伤威力。近年来，研究者对预制破片战斗部进行了大量工作。由于战斗部起爆后破片沿径向均匀向外飞散, 破片利用率低，为提高破片利用率，增强毁伤效果，聚焦战斗部、定向战斗部、轴向增强战斗部[1-3]技术应运而生。冯顺山等[1]提出了一种新的聚焦战斗部设计方法；严翰新等[4]数值模拟了不同起爆方式对聚焦战斗部性能的影响；邢恩锋等[5]研究了装药结构参数对轴向预制破片速度的影响；郭子云等[6]和刘洪峰等[7]进行了战斗部端面预制破片威力性能影响的数值仿真；张世林等[8]研究了轴向预制破片战斗部破片飞散特性的影响因素。

目前，基于预制破片及定向战斗部技术的战斗部径向破片场威力已经得到了很大的改善，但由于战斗部头部壳体较薄弱，所以常规战斗部仍存在轴向破片数量少、轴向杀伤威力不足的问题。为改善常规战斗部，尤其是防空战斗部轴向威力不足的缺点，本文中提出一种轴向威力增强战斗部结构。为充分利用爆轰波的能量，避免战斗部头部壳体因应力集中现象而过早破裂，设计一种圆弧形头部战斗部。通过在圆弧形头部战斗部外围均布球形预制破片以增加轴向破片数，提高爆轰波能量利用率，并有效控制预制破片的飞散角，保证弹丸头部一定角度空间域内都有破片存在。

1 数值模拟方法

战斗部结构如图1(a)所示，主要由壳体、炸药装药、预制破片、头壳组成。预制破片直径为5 mm，弹丸头部弧半径为R，弹丸壳体厚度为5 mm，装药直径为90 mm，装药高度为200 mm。为了与本文中提出的圆弧形头部轴向增强战斗部进行比较，设计了结构如图1(b)所示的战斗部结构。装药直径、壳体厚度、球形预制破片直径等参数保持不变。

利用显式有限元动力分析软件LS-DYNA对轴向预制破片战斗部爆炸驱动全过程进行数值模拟。炸药、预制破片及壳体均采用拉格朗日算法，网格单元采用六面体SOLID164单元。预制破片材料选用45钢，采用刚体材料模型，其密度为7.83 g/cm3，弹性模量为210 GPa，泊松比为0.3；炸药使用HIGH_EXPLOSIVE_BURN高能炸药材料模型和JWL状态方程描述；壳体材料选用45钢，采用PLASTIC_KINEMATIC材料模型。由于战斗部具有几何对称性，为了节省计算资源，建立1/4模型，并在对称面施加对称边界条件，材料模型及状态方程参数见表1和表2[9]，采用cm-g-μs-K单位制，其中ρ为密度，D为爆速，pCJ为爆压，A、B、R1、R2、ω为炸药参数，E0为初始内能，E为弹性模量，ν为泊松比，σy为屈服强度，Etan为切线模量，β为硬化参数，εf为失效应变。为了提高网格质量，网格划分前分别在平面及柱面坐标系下对预制破片、装药及壳体进行几何分割，使模型中每个部件均能满足映射法网格划分对几何实体形状的要求。此外，综合考虑计算精度与计算时长两个因素，预制破片、壳体及头壳、装药单元长度分别设置为0.062 5、0.10、0.09 cm，平板形头部、R=45，90 mm弧形头部3种战斗部模型分别划分为137 822、119 106和138 730个单元。由于炸药爆轰过程属于材料大变形过程，通常会导致炸药单元网格严重畸变，甚至导致程序无法正常运行。因此，为了使程序能够完全运行，在炸药爆轰结束后，及时将炸药单元删除[9]。

表1 8701炸药的材料参数和状态方程参数Table 1 Parameters of material and equation of state for 8701 explosive

表2 壳体材料参数Table 2 Material parameters of shell

2 数值模拟结果及分析

为验证所提出的战斗部结构能有效控制轴向预制破片的飞散角和飞散速度，在相同装药条件下分别对弧形和平板形头部预制破片战斗部进行了数值计算。同时，选取R=45，90 mm两种尺寸弧形头部战斗部，以研究头弧半径对预制破片飞散角的影响。图2～4给出了采用LS-DYNA程序计算所得不同工况下战斗部壳体膨胀变形、破裂贯穿、预置破片抛出、破片场形成的过程。

由图2～4可知：从起爆瞬时到t=12 μs，爆轰波呈理想的球面波；此后，由于装药长径比及弹丸壳体的约束，爆轰波曲率半径逐渐减小，当爆轰波到达弹丸壳体端部瞬时已近似呈平面波；在爆炸载荷驱动下，弹丸壳体破裂产生裂纹并逐渐贯穿，最终形成自然破片。图2中自然破片主要分布在弹丸周向，头部及底部只有少量大块自然破片，这是由于战斗部头部和尾部壳体较薄弱，同时由于应力集中效应，在弹丸头部和尾部与圆柱部连接处过早形成裂纹，致使炸药爆轰产生的能量过早外泄，未能充分作用于战斗部头部和尾部壳体。球形预制破片在爆炸载荷驱动下向弹丸头部所在方位飞散，预制破片较集中的分布于弹丸轴线附近，破片近似沿弹丸轴线直线运动。图3显示，随着爆轰波的传播，爆轰波曲率半径逐渐减小，并在40 μs左右趋于平直状态。大部分自然破片均匀分布在弹丸周向，少量大块自然破片分布在轴向，与图2相比，弹丸头部自然破片场有所改善，这是由于弧形头部战斗部头弧部过渡平滑，减小了应力集中效应，炸药爆轰能量充分作用于头部壳体。图3中预制破片在弹丸头部所在区域内以一定角度向外飞散，通过合理控制起爆时间及战斗部轴向预制破片数目可有效增大战斗部轴向预制破片及自然破片场的封锁区域。与平板形头部战斗部相比，弧形头部战斗部结构可以有效改善杀伤战斗部轴向破片数量不足及封锁区域小的缺点。图4中爆轰波传播规律和图3相似，破片分布无明显差异。综合对比图2～4可知，平板形头部战斗部预制破片较集中分布在弹丸轴线附近，破片近似沿弹丸轴线直线运动，弧形头部战斗部预制破片相对较发散的分布在弹丸头部所在区域，使得弹丸头部所在区域一定角度内均有破片飞散，大大增强了战斗部的轴向威力。

为了验证提出的战斗部结构能使轴向预制破片飞散角增大，运用LS-PREPOST后处理软件获取预制破片沿各个方向分速度，并由此计算出预制破片的飞散角θ(预制破片速度与弹轴夹角)为：

(1)

式中：v为预制破片速度，vz为破片沿弹丸轴线方向的分速度。表3和表4分别给出了平板形头部以及R=90，45 mm弧形头部3种结构战斗部端点起爆时典型位置预制破片速度参数及运用式(1)计算得到的预制破片飞散角。图5～6分别为相应条件下典型位置预制破片飞散参数拟合曲线。

表3 平板形头部战斗部端点起爆典型位置预制破片飞散参数Table 3 Flying parameters of premade fragment for flat head warhead

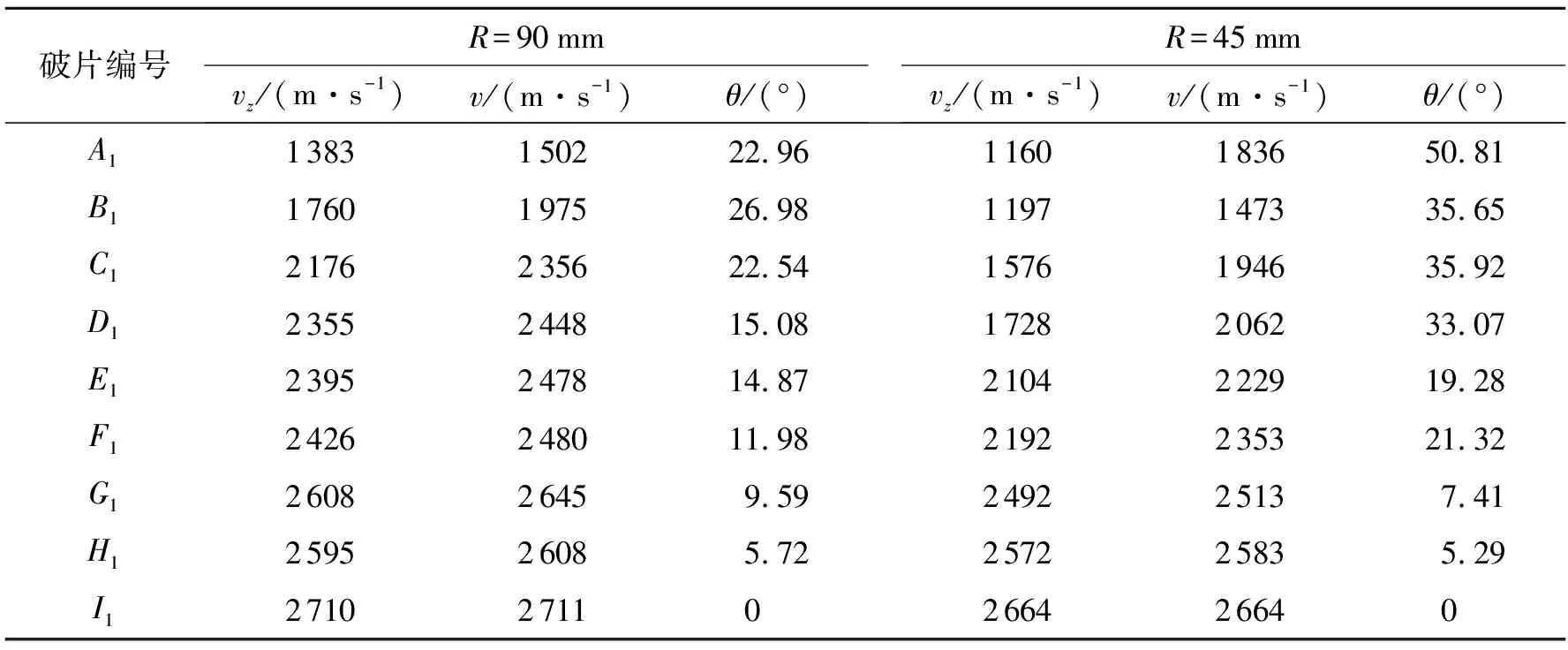
表4 弧形头部战斗部端点起爆典型位置预制破片飞散参数Table 4 Flying parameters of premade fragment for arc-shaped head warhead

由表3可知，平板形头部战斗部在端点起爆条件下的最大飞散角可达20.82°，从位置A2～G2，预制破片飞散角呈递减趋势，弹丸头部顶点处的预制破片基本沿弹轴方向飞散。预制破片的速度为1 530～2 220 m/s。由表4可知，R=45 mm圆弧形头部战斗部在端点起爆条件下的最大飞散角可达50.81°，从位置A1～I1，预制破片飞散角逐渐减小，弧形头部顶点位置处破片基本上沿着弹轴方向直线运动，预制破片速度为1 470～2 660 m/s。R=90 mm圆弧形头部战斗部的最大飞散角达到26.98°，预制破片速度为1 500～2 710 m/s。分析以上数据可知，当弧半径R=90 mm时，预制破片最大飞散角比平板形头部战斗部预制破片最大飞散角大6°左右，速度增益约为500 m/s；当弧半径R=45 mm时，预制破片最大飞散角比平板形头部战斗部预制破片最大飞散角大30°左右，速度最大增益约为440 m/s。对比弧半径R=45 mm和R=90 mm两种情况可知：弧半径R对预制破片最大飞散角影响很大，对最大速度的影响不明显；当弧半径R=45 mm时，预制破片最大飞散角约为R=90 mm时的两倍左右。

图5～7给出了平板形和R=90,45 mm弧形头部战斗部预制破片飞散角及飞散速度随位置的变化情况。由图5(a)、图6(a)和图7(a)可知，预制破片飞散角随位置近似呈线性变化，且图7(a)中曲线的斜率最大，图5(a)中曲线最平坦。图5(b)为平板形头部战斗部典型位置预制破片飞散速度的拟合曲线，可以看出，从位置A2～G2，破片速度近似线性递增，且A2与G2处破片速度相差较大，这是由于A2处稀疏效应比G2处大，且G2处有效装药量明显比A2处多。图6(b)和图7(b)分别为R=90和45 mm两种弧形头部战斗部典型位置处预制破片飞散速度的拟合曲线，可以看出，两种情况下，破片速度均随位置近似呈抛物线形变化，从位置A1～I1，曲线斜率逐渐减小，破片速度的增长越来越缓慢，且破片最大速度差比图5(b)中大很多，这是由于I1位于战斗部头弧顶部，此位置破片对应的有效装药量比A1处大很多。

图8给出了平板形和弧形头部战斗部(R=45和90 mm)预制破片打击迹线。由图8可知：弧形头部战斗部预制破片最大飞散角明显比平板形战斗部大；平板形头部战斗部轴向预制破片在±20.82°范围内均匀分布；R=45，90 mm弧形头部战斗部轴向预制破片分别在±50.81°和±26.98°范围内均匀分布。通过合理控制起爆时间，弧形头部战斗部的封锁区域将明显比平板形头部战斗部封锁区域大。表5为根据数值模拟结果计算出的预制破片分布参数，其中L为与起爆点的距离，S为封锁区域面积，N为破片密度。由表5可知，对于同种战斗部结构，随着距起爆点距离的增大，预制破片封锁区域逐渐增大，相应单位面积破片数量也急剧下降。在距离起爆点相同位置处，不同战斗部结构封锁区域及破片密度相差也很大，其中R=45 mm弧形头部结构战斗部封锁区域最大，虽然对应单位面积破片数量相对较少，但在距离起爆点7 m处单位面积依然有1个以上预制破片分布，满足对空间域的封锁条件。由此可知，采用弧形头部结构能够显著增大战斗部轴向封锁区域，大大增强战斗部的轴向杀伤威力。

战斗部类型L=3mS/m2N/m-2L=5mS/m2N/m-2L=7mS/m2N/m-2平板形4.086411.352322.2512弧形,R=90mm7.352420.35939.874弧形,R=45mm42.397118.093231.472

3 结 论

(1) 平板形和圆弧形头部战斗部头部均布的预制破片均能在弹丸头部所在空域中均匀飞散。不同的是，圆弧形头部结构战斗部预制破片飞散角最大可达到50.81°，而平板形头部战斗部预制破片飞散角最大只能达到20.82°。由此可知，采用圆弧形头部战斗部结构可以增大战斗部的封锁区域。

(2) 采用圆弧形头部能够有效增大轴向预制破片飞散速度，随着弧半径R的减小，速度增益有所减小，但可以增大预制破片的飞散角，当头弧半径取为0.5倍装药直径时，预制破片最大飞散角约为1倍装药直径时的2倍左右。在战斗部设计过程中，要综合考虑速度及飞散角两个因素，以确定合理的战斗部头部曲率半径。

(3) 通过对数值模拟结果的分析可以推测，当战斗部采用圆弧形头部，并在弹丸头部加装多层预制破片，可实现预制破片飞散角的连续控制，并显著增大防空战斗部的封锁区域。

参考文献:

[1] 冯顺山,黄广炎,董永香.一种聚焦式杀伤战斗部的设计方法[J].弹道学报,2009,21(1):24-26.

FENG Shunshan, HUANG Guangyan, DONG Yongxiang. A new design method of fragment focusing warhead[J]. Journal of Ballistics, 2009,21(1):24-26.

[2] 刘彤,钱立新,余春祥.破片聚焦战斗部的动态杀伤威力设计[J].爆炸与冲击,2005,25(6):536-540.

LIU Tong, QIAN Lixin, YU Chunxiang. A conception of the dynamic lethality for focused fragmentation warhead[J]. Explosion and Shock Waves, 2005,25(6):536-540.

[3] 魏继锋,焦清介,吴成.预制破片战斗部试验数值模拟研究[J].弹箭与制导学报,2004,24(3):39-41.

WEI Jifeng, JIAO Qingjie, WU Cheng. Experiment and simulation on premade fragment warhead[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004,24(3):39-41.

[4] 严翰新,姜春兰,李明.不同起爆方式对聚焦战斗部性能影响的数值模拟[J].含能材料,2009,17(2):143-146.

YAN Hanxin, JIANG Chunlan, LI Ming. Numerical simulation of effect of different initiation positions on a certain focusing fragment warhead[J]. Chinese Journal of Energetic Materials, 2009,17(2):143-146.

[5] 邢恩峰,钱建平,赵国志,等.炸药驱动预制破片轴向抛掷速度规律研究[J].火炸药学报,2007,30(3):30-33.

XING Enfeng, QIAN Jianping, ZHAO Guozhi, et al. Study on rule of the axial speeds of projection fragments drived by explosive[J]. Chinese Journal of Explosive and Propellants, 2007,30(3):30-33.

[6] 郭子云,赵太勇,陈智刚.战斗部端面预制破片威力性能影响的数值仿真[J].计算机仿真,2015,32(3):33-37.

GUO Ziyun, ZHAO Taiyong, CHEN Zhigang. Numerical simulation of lethality influence of warhead end premade fragment[J]. Chinese Journal of Computer Simulation, 2015,32(3):33-37.

[7] 刘洪峰,郭光全,卢士伟,等.战斗部轴向预制破片威力性能仿真与试验研究[J].中北大学学报,2015,36(增刊1):11-14.

LIU Hongfeng, GUO Guangquan, LU Shiwei, et al. Numerical simulation and test research of the warhead axial premade fragment power performance[J]. Journal of North University of China, 2015,36(Suppl 1):11-14.

[8] 张世林.轴向预破片战斗部破片飞散特性影响因素分析[D].太原:中北大学,2012.

[9] 时党勇,李裕春,张胜民.基于ANSYS/LS-DYNA 8.1进行显示动力分析[M].北京:清华大学出版社,2005.