空间太阳能电站姿态运动-结构振动耦合建模与分析

穆瑞楠，王艺睿，谭述君,4，吴志刚,4，齐朝晖

(1. 大连理工大学工业装备结构分析国家重点实验室，大连 116024；2. 中国科学院国家空间科学中心，北京 101408；3. 中国科学院大学，北京 101407；4. 大连理工大学航空航天学院，大连 116024)

0 引 言

空间太阳能电站(SSPS, Space Solar Power Station)是于1968年由美国科学家Peter Glaser提出的一种超大空间结构概念[1]。因其可实现连续工作、能量利用率高等诸多优点，近年来越来越受到各国和各研究机构的关注。不仅相继提出了数十种构型设计方案，在能量传输、在轨组装及动力学分析与控制等各个相关领域开展了大量工作[2]。由于尺寸和刚度的限制，这类超大空间结构很难在地面开展实验验证工作。因此，借助于仿真手段准确建模并分析其在轨的动力学特性至关重要。

绝大多数空间太阳能电站构型尺寸巨大[3]，通常设计为模块组装的方式在轨构建，包括杆件、薄膜、接口等基本组件，其建模难度高，模型包含的单元节点数目庞大，分析计算耗时较长，且不利于进行大量的参数分析。特别是对于其在轨的动力学分析，需要同时考虑其轨道运动和姿态运动，使得模型具有较高的非线性，进一步加大求解难度并降低求解效率。因此，对于空间太阳能电站的在轨动力学分析，基于其结构特点，将其简化为易于建模分析，并且具有一致动力学特性的简单结构十分必要。由于模块组装的在轨构建方式，其结构具有周期特性，因此采用基于能量等效原理的连续体等效方法最为合适。这种方法基于结构的周期性，不会因基本单元数量的扩充而导致计算量大幅增加，又能较好刻画结构的动力学特性。基于能量等效原理的连续体等效建模方法已有效应用于国际空间站主支撑桁架结构[4]以及大型环形可展天线的周边桁架结构[5]。

对于空间太阳能电站这种具有超大尺寸和超高柔性的空间结构，其尺寸达到公里量级，其轨道运动、姿态运动和结构振动之间的耦合作用不可忽略。一些学者对空间太阳能电站的耦合动力学开展了研究。Wie[6]基于Abacus电站构型，分析了环境干扰力作用下的轨道运动与姿态运动，提出了轨道-姿态耦合控制方案。吴志刚[7]基于太阳塔式构型，考虑地球扁率的引力场，在地球同步拉普拉斯轨道上研究了高阶重力和力矩对空间太阳能电站姿轨运动的影响，发现高阶力对轨道运动影响较大，而对姿态运动影响较小可忽略。同时，超大结构的结构振动引起了更多学者的关注。Malla[8]、Ishimura[9]和穆瑞楠[10]建立了轴向振动空间哑铃的轨道-姿态-振动耦合动力学模型，分别讨论了初始条件、系统参数以及结构尺寸对空间哑铃动力学特性的影响。在穆瑞楠的研究工作中特别提到结构振动引起了姿态运动周期的改变，在较大初始姿态角下可能引起姿态运动的翻滚现象。Silva[11-12]和Liu[13]以柔性梁为研究对象，前者给出了柔性梁的非线性扰动方程，并用扰动分析方法讨论了系统可能出现的共振现象；而后者考虑动力刚化效应，提出了参数激励模型(PEM)，该模型可以更加精确地描述超大柔性空间结构在持续转动时的结构振动。魏乙[14]将JAXA绳系构型简化为集中质量-绳索-板模型，基于绝对节点坐标法建立了耦合动力学方程，提出了结合辛Runge-Kutta方法的微分-代数方程求解方法，分析了系统参数对耦合特性的影响并验证了求解方法的有效性。

本文基于能量等效的原则，将空间太阳能电站等效为柔性梁模型，并考虑重力梯度影响，建立姿态运动-结构振动耦合动力学模型；提出Runge-Kutta法和Newmark法相结合的耦合动力学方程的高效求解方法；最后对比不同参数下的仿真结果，并对超大柔性梁模型的在轨耦合特性进行讨论。

1 连续体等效建模

基于能量等效的连续体等效方法既可应用于桁架结构，也可应用于框架结构，只需要结构具有周期性。多旋转关节空间太阳能电站(MR-SPS)构型的支撑部分为桁架梁组成的平面框架结构，可分解为周期框架模块和周期桁架模块。首先针对周期桁架模块，将桁架梁等效为连续梁模型；然后针对周期框架模块，从而得到整体的等效连续梁模型。基于能量等效原理的连续体等效建模的理论方法如下。

周期模块的各根构件简化为杆或梁模型。定义构件局部坐标系原点位于构件中心，其x1轴方向沿构件方向。每根构件的变形为沿x1轴的拉伸变形以及绕y1轴和z1轴的弯曲变形，而其运动为质心沿x1轴、y1轴和z1轴的平动与绕质心转动。周期模块总的变形能和动能可表示为

(1)

(2)

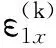
将周期模块内各点位移和应变在周期模块整体的几何中心处Taylor展开，则可将周期模块任一横截面上各点的位移和应变用周期模块中心处的位移和转角及应变和曲率表示，即

u=Γuuc+Γεεc

(3)

其中uc表示周期模块中心处的位移与转角，而εc表示其应变与曲率，Γu和Γε分别为对应的展开系数矩阵。将式(3)代入式(1)和式(2)即可得到以中心点位移和应变描述的周期模块的变形能和动能。

另一方面，可建立与模块相同长度的等效梁模型的变形能及动能。将等效梁模型在模块长度内的位移及应变近似为均匀，则以中心点位移和应变描述的变形能和动能表达式分别为

(4)

(5)

其中L为模块长度。

分别对比周期模块和等效梁模型的变形能和动能表达式，可得结构的等效关系为

(6)

(7)

2 在轨柔性梁的动力学建模

基于哈密顿原理，考虑重力梯度影响，建立柔性梁的姿态运动和结构振动的耦合动力学模型。将地球视为理想球体，用Oe表示地心，柔性梁在轨道平面内绕地球运动，如图1所示。

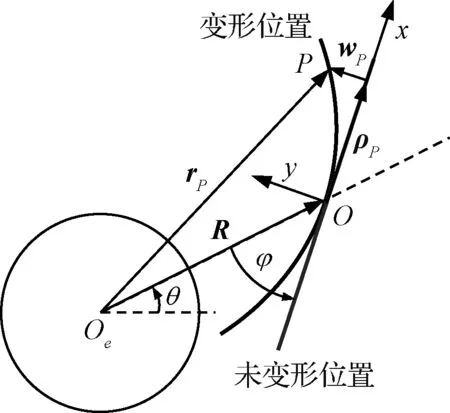
图1 柔性梁结构在轨运行示意图Fig.1 Schematic diagram of flexible beam structure in orbit

以柔性梁几何中心的运动作为其轨道运动，轨道半径R由地心指向柔性梁几何中心，指向近地点的长半轴方向与轨道半径矢量方向之间的夹角θ为轨道角，并用ωo表示轨道角速度。选取柔性梁几何中心O为原点，柔性梁几何中心处切线方向为x轴方向，建立柔性梁的固联浮动坐标系，则轨道半径矢量方向与浮动坐标系x轴方向的夹角φ为面内姿态角，梁上各点偏移浮动坐标系x轴的横向位移为弯曲变形。坐标量ρP由几何中心O到点P变形前位置；横向变形量wP由点P变形前位置指向变形后位置。则梁上点P相对于地心的位置rP为

(8)

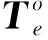
(9)

其中mP表示点P的处的结构质量，即线密度。

对点P的动能式(9)在结构长度上积分，得到整体柔性梁的动能为

(10)

对于在轨柔性梁结构而言，其势能包含重力势能和变形能两部分。这里考虑的柔性梁为纯弯曲梁模型，其应变能与教材中给出的欧拉梁应变能一致[15]。因此柔性梁的总势能为

(11)

其中μ为地球引力常数，EI为柔性梁的弯曲刚度，r为梁上某点到地心的距离，表示为

r2=(R2+x2+w2+2xRcosφ-2wRsinφ)

(12)

无非保守力做功的Hamilton原理为

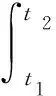
(13)

将柔性梁的动能式(10)和势能式(11)代入式(13)，得到柔性梁的在轨姿态-振动耦合动力学方程为

(14)

(15)

注意到耦合动力学方程中与重力梯度有关的项含有(r-3)项，该非线性项难以用有限元方法处理，因此需要将其近似展开。由式(12)得(r-3)的二项式展开为

(16)

其中参数ε=x/R,表示结构尺寸与轨值半径之比上式近似保留至参数ε的二次项以及w的线性项。将式代入式和式得到近似耦合动力学方程，其中含有参数ε的一阶项和二阶项分别对应于重力梯度力/力矩的一阶项和二阶项。

由于柔性梁的在轨耦合动力学方程既包括偏微分方程，又含有在结构长度上的积分项，因此采用有限元方法将结构离散，引入只与时间t有关的节点位移变量和只与位置变量x有关的形函数，从而消去方程中关于位置变量x的微分和积分。梁上某点弯曲变形重新表述为

w(x,t)=N(x)ae(t)

(17)

其中N(x)表示单元内的形函数，ae(t)表示单元内的节点位移，这里梁单元采用经典的二节点Hermite单元。基于有限元理论[15]，利用梁横向变形的新形式，可将在轨耦合动力学方程式(14)和式(13)分别转化为

(18)

(19)

其中J为柔性梁面内转动惯量，M和K分别为柔性梁质量阵和刚度阵，TG1和TG2分别为重力梯度力矩的一阶项和二阶项，PG1和PG2分别为重力梯度横向分力的一阶项和二阶项。各项的表达式如下

其中Φ0、Φ1和Φ2是用于简化标记的矩阵和向量，其表达式为

3 模型参数及求解方法

多旋转关节空间太阳能电站示意图以及其中作支撑骨架的结构力学模型如图2(a)所示，其整体结构由具有周期性的框架结构组成，而周期框架结构中的单根构件又是由具有周期性的桁架结构组成。桁架周期模块和框架周期模块以及它们的整体坐标系如图2(b)和(c)中蓝色虚线(见电子版)框所示。

多旋转关节空间太阳能电站构型的几何尺寸如表1所示，各杆件选用T700碳纤维复合材料，其材料参数在表1中给出。

利用基于能量等效的连续体等效方法，将该构型等效为矩形等截面的均匀质量柔性梁模型，其弯曲刚度EI= 1.56×109N·m2，密度与横截面积的乘积(线密度)ρA= 6.20 kg/m。等效梁模型的结构基频为4.058 × 10-4Hz，而多旋转关节构型的有限元模型的基频为3.841 × 10-4Hz，二者不仅具有相同量级，且差别仅为5%，能够反应其动力学现象。

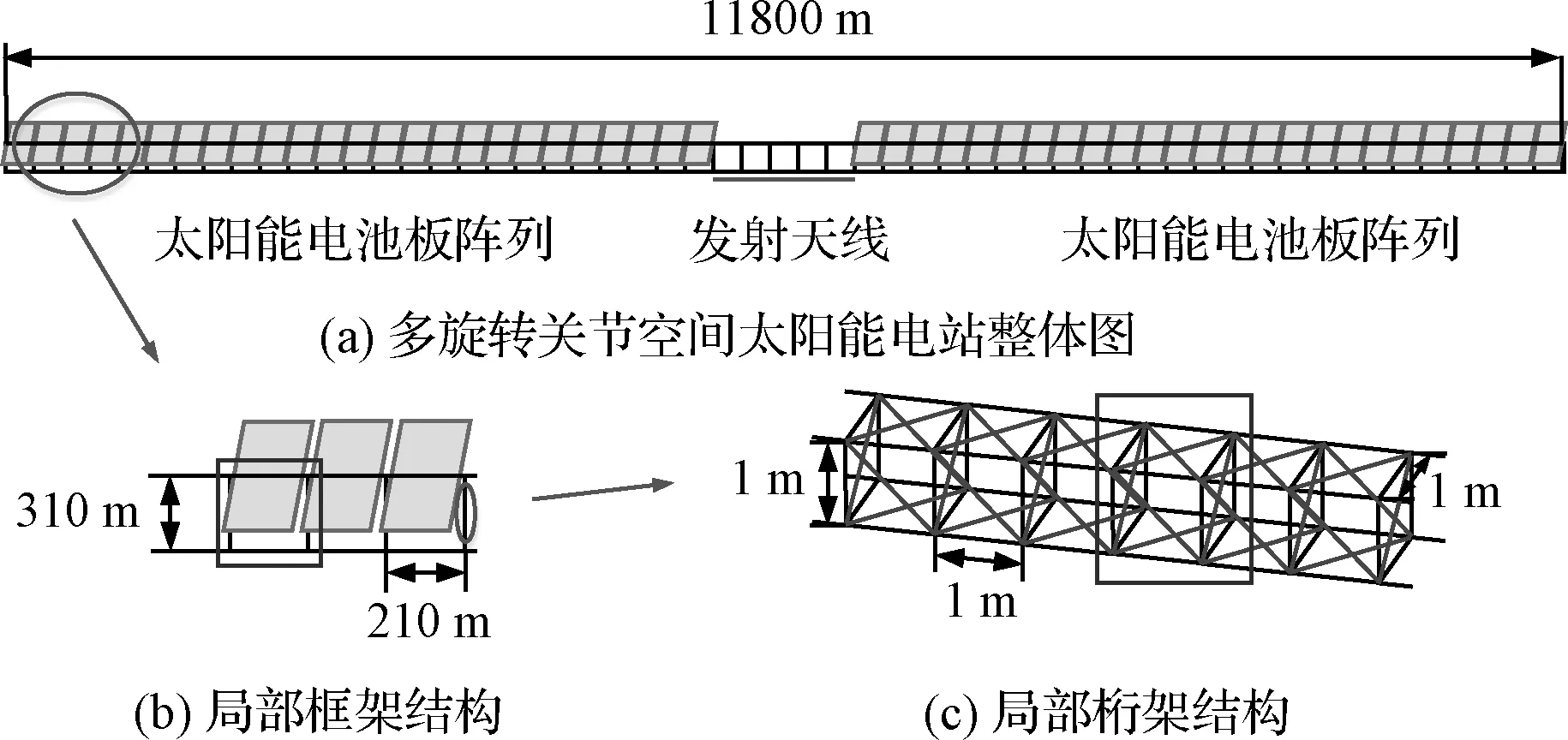
图2 桁架和框架周期模块示意图Fig.2 Diagram of truss and frame periodic modules

桁架模块尺寸1 m×1 m×1 m框架模块尺寸210 m×310 m总长度11.8 km杆件截面积2.359 cm2杆件弹性模量248 GPa杆件密度1750 kg/m3

涉及到的常数有：地球平均半径RE=6378 km，地球引力常数为μ=3986 00 km3/s2。这里主要研究大尺寸结构在低轨道(LEO)和地球同步轨道(GEO)下的动力学现象。选取柔性梁所处的低轨道的高度为322 km(即几何中心轨道半径R=6700 km)，此时的轨道频率为1.833×10-4Hz，而地球同步轨道的高度为35 786 km(即几何中心轨道半径R=42 164 km)，此时的轨道频率为1.161×10-5Hz. 同时，结构尺寸是结构基频的重要影响因素，因此在50 m～10 000 m之间选取一系列值作为对比。初始姿态角对姿态运动幅度有很大影响，这里取两种情况：小姿态角(φ0=0.1 rad)和大姿态角(φ0=π/4 rad)；其他初始条件均设置为零。

在求解耦合方程式和式时，由于其已被转化为二阶常微分方程组，因此可采用经典的Runge-Kutta 法求解。但由于有限元离散后的节点较多，使得方程维数较大，因此直接采用这种方法求解效率低。由于姿态和振动方程中系数相互包含，耦合求解时具有强非线性，因此难以使用常用的有限元方程求解方法Newmark法。对于非线性微分代数方程缺乏有效且高效的求解方法是超大柔性空间结构耦合动力学研究所面临的问题之一。本文将两种方法结合，提出了Runge-Kutta 法和Newmark法同时迭代的方法，具体过程如图3所示。与应用Runge-Kutta法求解耦合方程相比，本文提出的方法在保证求解精度的同时效率大幅提升。在低轨道、小初始姿态角、结构尺寸为1000 m的条件下，仿真时长1000 min，时间步长为0.1 s，本文提出的方法在效率上提高约752倍，两种方法得出的响应相差5.36%. 后续仿真结果均基于本文提出的改进方法得出，其中时间步长取为0.1 s。

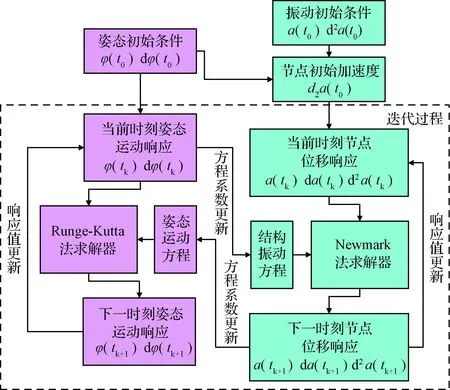
图3 改进的耦合模型求解算法流程图Fig.3 Flow chart of improved algorithm for coupling model

在利用提出的方法求解动力学响应时，姿态运动方程式(18)中含有未知的初始加速度响应，无法开始迭代。因此利用振动方程式(19)简化姿态方程得

(20)

其中

4 姿态-振动耦合特性

4.1 结构振动幅值影响分析

从结构振动方程式(19)可以看出，姿态运动对结构振动既有惯性力的直接影响，也有改变重力梯度分力的间接影响。若忽略结构变形对姿态运动的影响，则姿态运动方程式(18)可简化为

(21)

将式(21)代入结构振动方程(19)中发现，方程右端第一项(角加速度项)与第二项(重力梯度一阶项)的一部分相互抵消，则结构振动方程整理为

(22)

由上式可以看出，重力梯度的二阶项PG2是激发结构振动的主要因素，姿态运动通过重力梯度的二阶项PG2对结构振动的间接影响。图4分别给出了不同轨道下的大幅度姿态运动下的结构振动响应。由重力梯度的二阶项PG2的表达式可知，该项大小随轨道半径的增加反比例变化，同时以轨道角速度的平方量级减小，因此不同轨道下的振动量级近似相差3个量级。

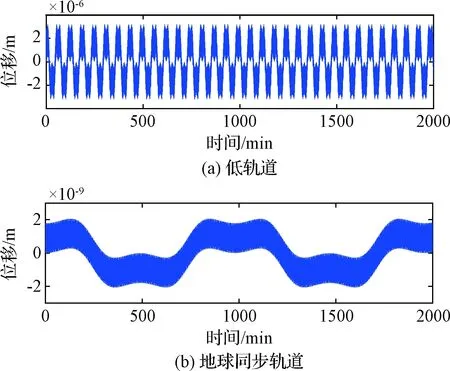
图4 大幅度姿态运动下的结构振动响应Fig.4 Structural vibration response under attitude motion with large magnitude

由前文中的重力梯度的二阶项PG2表达式可以看出，该项与质量阵的比值以结构尺寸的二次方量级增加。同时，刚度阵与质量阵的比值以结构尺寸的四次方量级减小。因此当结构基频远大于姿态运动频率时，振幅以结构尺寸的6次方量级增加。

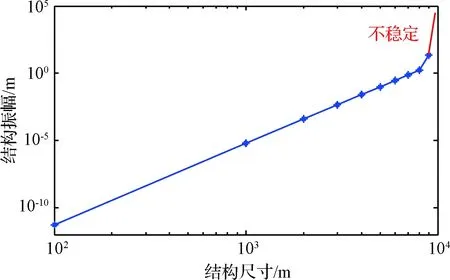
图5 结构尺寸与振动幅度变化关系(LEO)Fig.5 Relationship between structural vibration magnitude and structure size(LEO)

图5给出了低轨道下的结构振幅随结构尺寸变化结果，在尺寸较小时，结构振幅量级变化规律与理论结果一致，即按结构尺寸的6次方量级增加。但仿真发现，结构尺寸过大会引起系统不稳定现象。以本文的参数为例，低轨道下结构尺寸接近9450 m时，结构振幅增长速度加快，最终系统运动发散。这种不稳定现象对应的临界尺寸与结构柔性和轨道高度有关，轨道高度增加则对应的临界尺寸增大。

4.2 结构振动频率影响分析

由简化的结构振动方程式(22)可以得到结构振动的第一阶频率为

(23)

其中ωs为结构基频。从式(23)可以看出，结构振动频率受到转动耦合项(等式右端第二项)以及重力梯度项(等式右端第三项)的影响，使结构振动周期出现波动现象。

考虑到在无控情况下姿态运动接近于正弦振动，因此将姿态运动近似表示为φ=φocos(κωot)，其中φ0为初始姿态角，kωo为姿态运动频率，k与φ0的取值相关，可通过与仿真得到的姿态运动响应拟合得到。将近似的姿态运动代入式(23)并无量纲化得

1-3sin2(φ0coskωot)

(24)

注意到，式(24)中的转动耦合项和重力梯度项中的轨道角速度处于三角函数内，因此轨道角速度主要对频率比的变化周期有影响，对幅值影响较小。

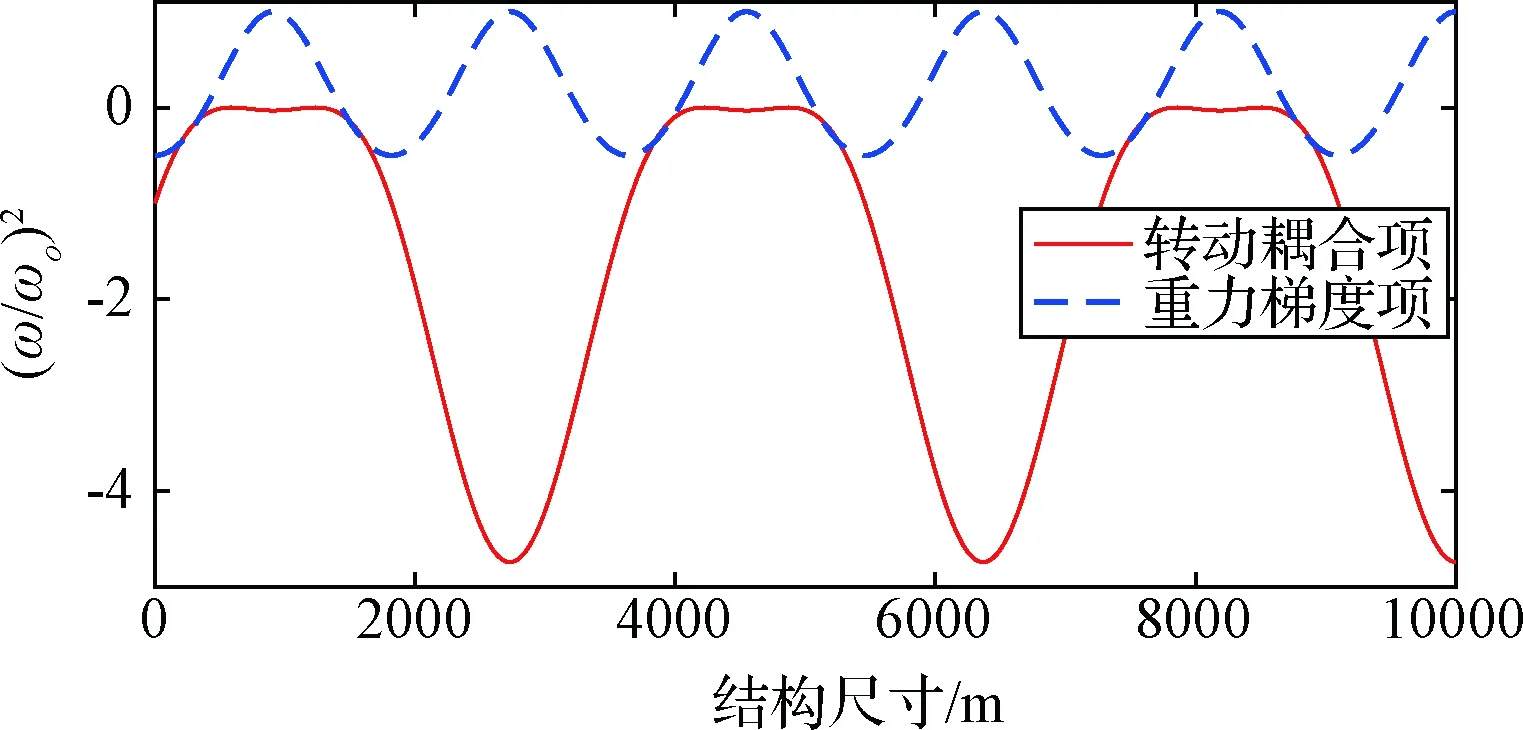
图6 姿态运动和重力梯度对振动频率的影响(φ0 = π/4 rad)Fig.6 Effects of attitude motion and gravity gradient on frequency of structural vibration (φ0 = π/4 rad)

图6给出了低轨道大幅姿态运动下的转动耦合项和重力梯度项对结构振动频率随时间变化的影响曲线。对于大幅姿态运动(φ0=π/4 rad)，对应的k=1.5003，从图6可以看出，重力梯度项波动幅度增大至一倍轨道频率，时而使结构振动频率增大，时而使其减小。转动耦合项仍使结构振动频率降低，其量级增大至两倍轨道频率。小幅姿态运动下的结果类似，但幅值较小。

当结构基频极低时，由式(23)可知结构可能发生屈曲的失稳现象，文献[13]中对惯性稳定的柔性梁的分析中也提及了这种现象。将令式(23)左侧最小值等于0的结构基频称为临界结构基频。则对于不同幅度姿态运动，对应的临界结构基频也不同。临界基频ωb满足

1+3sin2(φ0coskωot)}

(25)

利用正弦函数的泰勒展开，以及二项式展开公式，式(25)右端括号内的表达式可以转化为参数λ的四阶多项式形式。

(26)

其中λ=sinkωot。对式(20)求导并分析发现其导数表达式只有一个实根，同时该式的最高阶的四次项系数为负，因此在全局有且只有一个极大值。对其导数表达式应用一元三次方程求根公式，得到该极值点为

(27)

同时注意到λ在[-1,1]范围内取值，若极值点不在取值范围内则最大值点在边界取值。经数值验证，在初始姿态角φ0在[0 , 0.476π]时，最大值在λ = -1处取得，则临界振动频率ωb满足

(28)

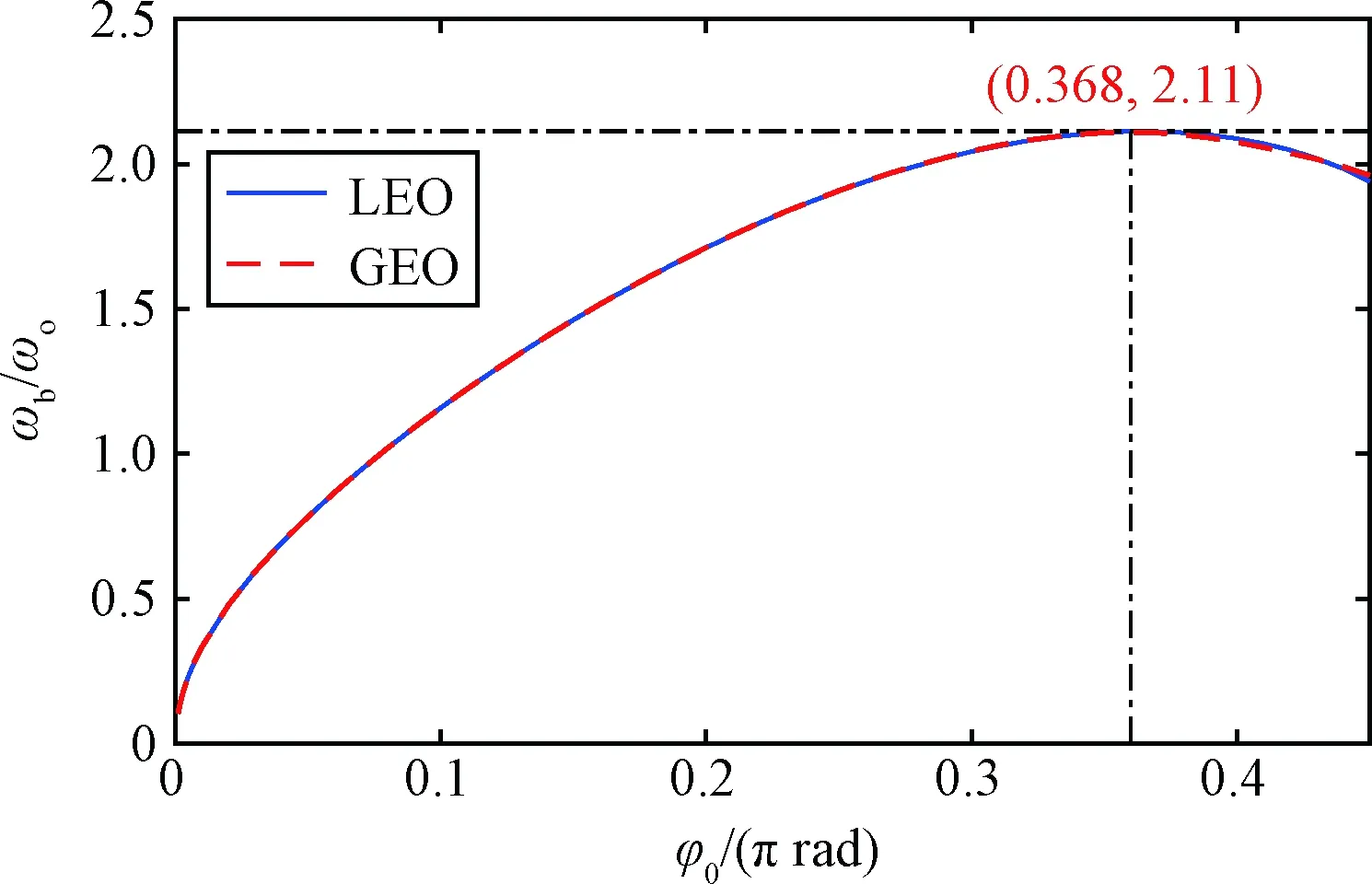
图7 临界振动频率随初始姿态角变化曲线Fig.7 Variation of critical frequency of structural vibration with respect to initial attitude angle

图7根据式(28)给出了低轨道和地球同步轨道下的临界振动频率随初始姿态角变化曲线，发现不论在低轨道还是地球同步轨道，耦合作用对结构振动频率的影响都存在。初始姿态角在0.386π rad时临界振动频率最大，此时影响幅值约为2.11倍轨道频率。因此，在设计梁式空间结构时，考虑耦合作用对结构振动频率的影响，才能保证结构不会发生屈曲不稳定现象。

4.3 结构振动对姿态运动的影响

若引入小角度假设条件，并忽略结构振动对转动惯量的影响，则姿态运动方程简化为

(29)

其中

仅考虑柔性梁一阶振型的振动，令

a=w0Ω(x)sin(ωst)

(30)

其中w0为最大振动幅值，Ω(x)为一阶振型。将式(30)代入式(29)，得到姿态运动有系统阻尼的自振频率ωa为

(31)

其中阻尼比为

(32)

阻尼比的最大值可表示为

(33)

其中α是系统常数，与材料属性、梁振型等参数有关。由式可以看出，姿态运动频率受结构振动幅度和结构尺寸的影响。结构振动幅度增大时，姿态运动频率降低。同时注意到结构振动幅度与结构尺寸的6次方量级关系，因此结构尺寸增加也导致姿态运动频率降低。

图8分别给出了小幅度姿态运动(φ0=0.1 rad)和大幅度姿态运动(φ0= π/4 rad)下的刚体与柔性体姿态角响应对比。为了显示出柔性引起的姿态周期变化，图中截取了仿真时间3200～3300 min的结果。从图中可以发现，随着仿真时间增加，柔性体姿态运动越来越偏离刚体的姿态运动，即柔性体姿态运动周期较大。对比两图发现，初始姿态角越大，这种结构柔性引起的姿态运动周期增大现象越明显，这是由于初始姿态角越大，姿态运动引起的结构振动幅度越大，反过来使得姿态运动阻尼比越大，因此姿态运动周期增大就越明显。

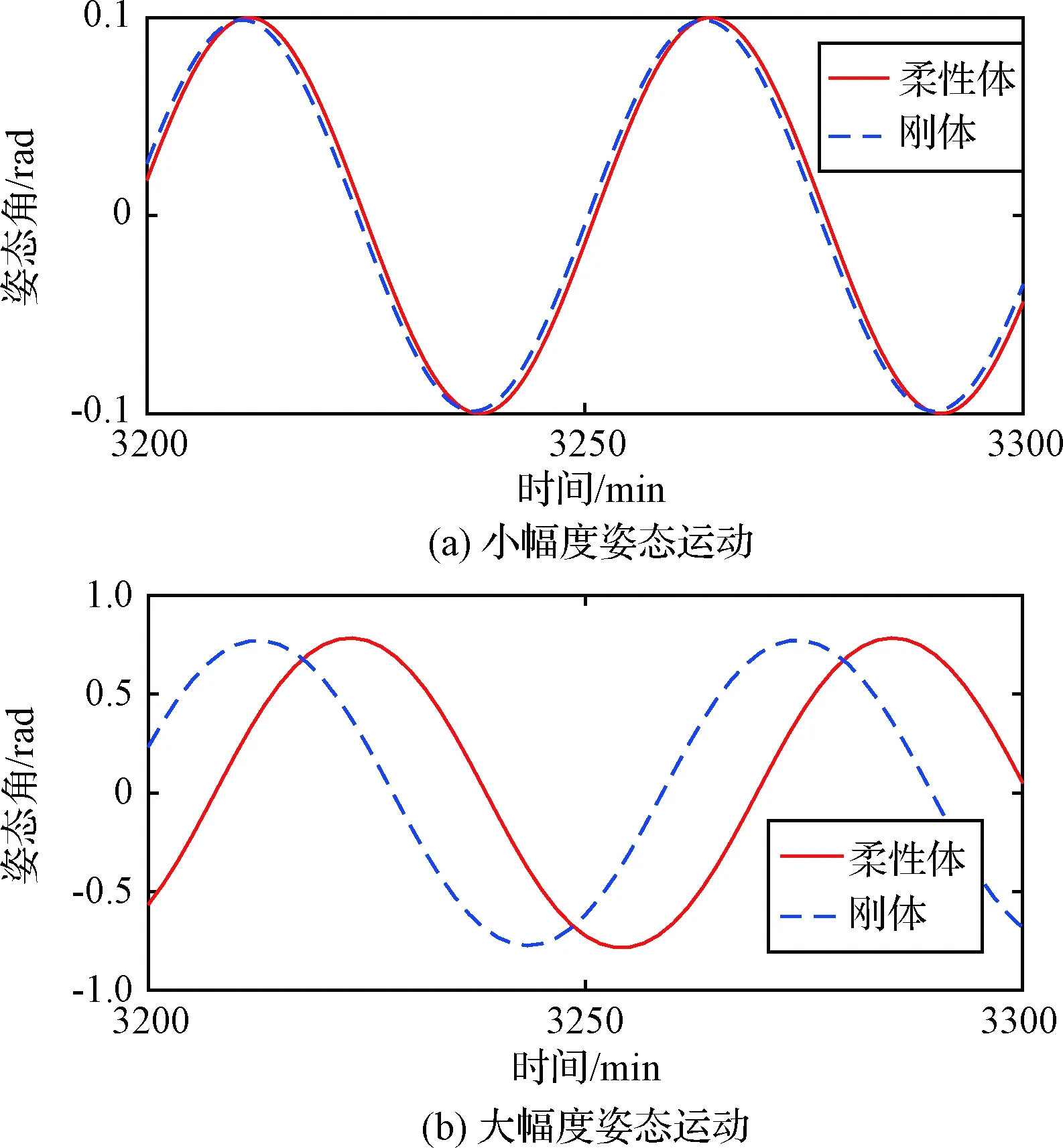
图8 柔性体与刚体的姿态角响应比较(LEO)Fig.8 Comparison of attitude angle between flexible and rigid model(LEO)

图9给出了地球同步轨道下的大幅度姿态运动时的刚柔结构姿态角响应结果对比，结构柔性引起的姿态运动周期增大现象仍然存在。分析式(33)可知，轨道角速度降低原本是会增大姿态运动阻尼比，但是由图4可知此时结构振动幅度大幅下降，因此在地球同步轨道下刚体和柔性体的姿态运动周期差别较小。

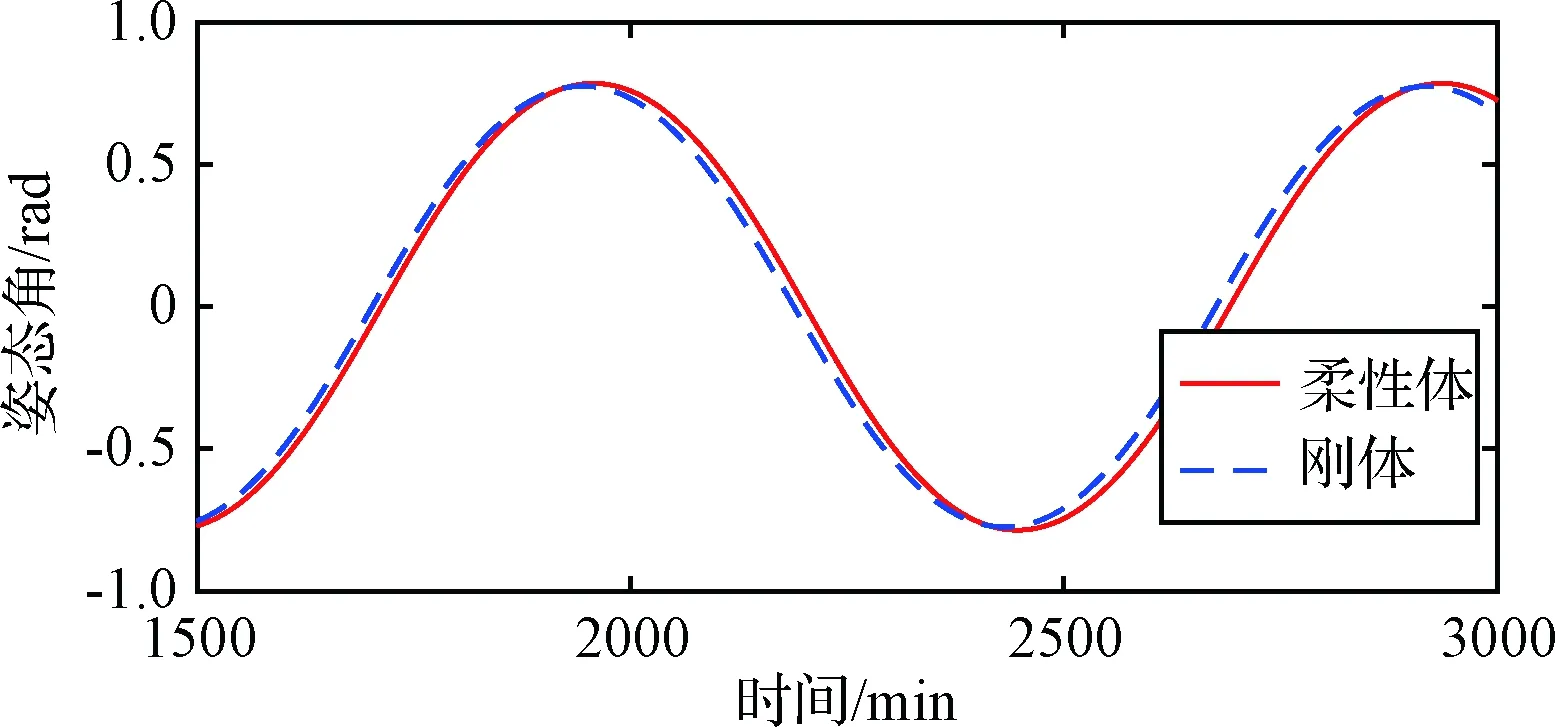
图9 柔性体与刚体的姿态角响应比较(GEO)Fig.9 Comparison of attitude angle between the flexible and rigid model(GEO)

5 结论与展望

本文将MR-SPS电站构型等效为柔性梁模型，并考虑重力梯度影响，建立了姿态运动和结构振动耦合动力学模型，利用改进算法分析了不同参数取值下两者耦合关系。得到主要结论如下：1)所提出的基于Runge-Kutta 法和Newmark法的改进算法适用于姿态运动-结构振动耦合方程求解，大幅提高了计算效率；2)在轨柔性梁模型中的重力梯度项至少近似保留至ε的二阶展开项，尺寸过大可能导致结构屈曲不稳定；3)姿态运动和结构振动耦合效应导致结构振动频率降低，姿态运动周期增大，在GEO轨道仍有这种现象。为保证系统在轨稳定性，超大型空间结构设计时应考虑耦合因素影响，并需要进一步开展与结构振动抑制协同的姿态控制策略研究。

参 考 文 献

[1] Glaser P E. Power from the sun: its future[J]. Science, 1968, 162(3856):857-861.

[2] 侯欣宾, 王立. 空间太阳能电站技术发展现状及展望[J]. 中国航天, 2015, (02):12-15. [Hou Xin-bin, Wang Li. Present situation and prospect for the solar power station [J]. Space System and Technology, 2015, (02):12-15.]

[3] 侯欣宾, 王立, 张兴华等. 多旋转关节空间太阳能电站概念方案设计[J]. 宇航学报, 2015, (11): 1332-1338. [Hou Xin-bin, Wang Li, Zhang Xing-hua, et al. Concept design on multi-rotary joints SPS [J]. Journal of Astronautics, 2015, (11): 1332-1338.]

[4] Noor A K, Mikulas M M. Continuum modeling of large lattice structures: status and projections[M]// Atluri S N, Anthony K A. Large space structures: dynamics and control. Heidelberg, Berlin: Springer, 1988:1-34.

[5] 刘福寿, 金栋平. 环形桁架结构径向振动的等效圆环模型[J]. 力学学报, 2016, 48(5):1184-1191. [Liu Fu-shou, Jin Dong-ping. Equivalent circular ring model for the radial vibration analysis of hoop truss structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(5):1184 - 1191.]

[6] Wie B, Roithmayr C M. Attitude and orbit control of a very large geostationary solar power satellite[J]. Journal of Guidance, Control, and Dynamics. 2005, 28(3):439-451.

[7] 吴志刚, 刘玉亮, 张开明, 等. 高阶重力和力矩对空间太阳能电站运动的影响[J]. 空间控制技术与应用, 2016, 42(4):1-5. [Wu Zhi-gang, Liu Yu-liang, Zhang Kai-ming, et al. The influences of higher order gravitational force and torque to the motion of space solar power station [J]. Aerospace Control and Application, 2016, 42(4):1-5.]

[8] Malla R B. Structural and orbital conditions on response of large space structures[J]. Journal of Aerospace Engineering, 1993, 6(2):115-132.

[9] Ishimura K, Higuchi K. Coupling among pitch motion, axial vibration, and orbital motion of large space structures[J]. Journal of Aerospace Engineering, 2008, 21(2):61-71.

[10] 穆瑞楠, 谭述君, 吴志刚. 重力梯度对超大柔性空间结构在轨动力学特性的影响[J]. 国防科技大学学报, 2017, 39(3):7-14. [Mu Rui-nan, Tan Shu-jun, Wu Zhi-gang. Effect of gravity gradient on dynamical characteristics of very large flexible space structures in orbit[J]. Journal of National University of Defense Technology, 2017, 39(3):7- 14.]

[11] Dasilva M M, Zaretzky C L. Nonlinear dynamics of a flexible beam in a central gravitational field—I. equations of motion[J]. International Journal of Solids and Structures. 1993, 30(17):2287-2299.

[12] Dasilva M M, Zaretzky C L. Nonlinear dynamics of a flexible beam in a central gravitational field—II. nonlinear motions in circular orbit[J]. International Journal of Solids and Structures. 1993, 30(17): 2301-2316.

[13] Liu Y, Wu S, Zhang K, et al. Parametrical excitation model for rigid-flexible coupling system of solar power satellite[J]. Journal of Guidance, Control, and Dynamics. 2017:1-8.

[14] 魏乙, 邓子辰, 李庆军,等. 绳系空间太阳能电站动力学响应分析[J]. 宇航学报, 2016, 37(9): 1041-1048. [Wei Yi, Deng Zi-Chen, Li Qing-jun, et al. Analysis of dynamic response of tethered space solar power station [J]. Journal of Astronautics, 2016, 37(9):1041-1048.]

[15] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003:306-311.