基于广义线性混合模型的驾驶员路径选择行为分析

程邦录，干宏程 （上海理工大学 管理学院，上海 200093）

0 引 言

随着城市规模的不断扩大和车辆数量的不断增加，人们面临着日益增长的交通压力，如何解决道路拥挤问题是城市规划设计者面临的重要问题。在众多解决方案中，快速路网由于其可以解决长距离交通问题的特点被广泛应用在城市交通建设中。在城市快速路网的建设过程中，也在不断加入科技元素，利用智能交通系统（Intelligent Traffic System，ITS）中先进的技术辅助快速路网的管理，是未来交通的发展方向。先进交通信息系统（Advanced Traffic Information System，ATIS）是ITS中重要的子系统之一，可变信息板（Variable Message Sign，VMS）是主要用来优化路网的ATIS设备之一。但是，由于交通路网的复杂性，VMS在实际运用的过程中，还有很多问题需要进一步完善和解决。

目前，国外的学者们都从不同的角度对VMS在信息诱导方面做了大量研究，其中不乏通过建模或算法仿真对VMS影响驾驶员行为方面进行讨论。Markos Papageorgiou（1990）对快速路网上的动态交通进行建模，进行了有关道路引导方面的研究[1]；Said Mammar（1996）分析了丹麦奥尔堡市VMS的设计与实施，评价了快速路网的运行效益，同时提出了改进建议[2]；Jiajun Wang（2013）从有效性和总成本最小的角度，利用多目标优化模型，对VMS信息效用的最大化进行研究[3]。

近些年来，国内很多城市积极建设快速路网，大力发展智能交通，大量的信息技术被运用在交通领域。在这一背景下，越来越多的国内研究者关注到这一领域，进行调研分析，为交通路网的建设提供建议。石小法、王炜、李文权（2001）利用随机均衡模型论证了提供交通信息是一种提高交通网络效率的有效方法[4]；曾松等（2002）通过驾驶员调查和计算机仿真对驾驶员的路线选择行为进行研究，利用多元Logit模型分析了驾驶员在行程时间信息的影响下对不同路线的选择，讨论了改变到非常规路线的可能性[5]；熊秩、黄海军、李志纯（2003）将出行者分为怀疑保守型和信任乐观型两类，建立了一个等价的随时间演进的随机用户均衡模型[6]；干宏程、孙立军、陈建阳（2006）针对上海市快速路交通诱导系统，研究了VMS对驾驶员出行途中改道的问题，利用离散选择方法分析数据，建立了多元Logit模型[7]；尚华艳、黄海军、高自友（2008）采用元胞传输模型，针对重复性拥挤和非重复性拥挤两种交通状态下，对VMS对交通流的影响进行了分析[8]；干宏程（2010）运用意向调查方法采集了行程时间和其波动性对驾驶员路径选择行为影响的数据，采用离散选择建模方法估计了二元Probit模型用来描述路径选择概率[9]。

综合来看，现有的研究存在着两点值得改进的地方。第一，针对驾驶员的路线选择调查数据一般是分类数据，通常不满足正态分布，因此在利用经典线性模型进行回归估计时会产生偏差。第二，调查数据的样本并不是相互独立的，同一位驾驶员在面对不同交通情景时作出的判断具有关联性，这当中涉及到了个体的固定效应和随机效应，在数据处理的过程中应当格外关注。

现阶段，广义线性混合模型是解决上述问题的首要选择。该模型由经典线性模型发展而来，通过引入链接函数解决了变量为非正态分布的问题，而且通过引入随机效应来分析数据间的相关性问题。因此，本文采用广义线性混合模型来进行驾驶员路径选择问题的实证分析，期望可以得到影响驾驶员路径选择的更为准确的结论[10]。

1 驾驶员路径选择行为调查与分析

本文的问卷调查采用了行为调查（Revealed Preference，RP），以及意向调查 （Stated Preference，SP）结合的方式。RP调查是针对实际的情况而进行的一种调查，反映被调查者的具体属性及其在现实的生活中真实情况的选择，SP调查则是针对被调查者的意愿或者是态度，反映被调查者在虚拟的情境中对不同的情况做出的偏好程度及其选择情况。

RP调查的内容主要包括：（1）使用高架快速路的频率（几乎每天，每周3～4天，每周1～2天，几乎不用）；（2） 是否了解VMS（非常了解，比较了解，不太了解，完全不了解）；（3） 对VMS的关注度（时刻关注，经常关注，很少关注，不关注）。SP调查的主要内容是假设当VMS给出不同的信息（颜色和文字）时，驾驶员是否会改变原定的驾驶路线。本文模拟的情景是驾驶员驾车前往龙华路，原计划从龙华西路下匝道，离开高架道路，到达目的地。当关注到VMS给出的前方道路信息后，是否会提前从漕溪路匝道离开高架走地面道路到达目的地。调查问卷提供了6种VMS假设，为3种路径颜色组合（黄、红、黄+红）与2种拥堵原因描述（事故拥堵、非事故拥堵）的搭配组合，调查中使用的图像如图1所示：

对应说明如表1所示：

图1 SP调查中使用的图像

表1 SP调查中使用的图像描述

基础问卷部分包括受访者的性别、年龄、驾龄、汽车类型等问题，针对年龄、驾龄等连续进行离散化处理，被调查者根据实际情况进行单项选择。调查方式为现场发放问卷和网络问卷结合的方式，实地调查地点为上海市浦东新区杜鹃路一家司机快餐店和附近洗车场。共获得问卷109份，其中有效问卷96份，经过处理后得到576条（96×6）有效记录，这就是本文建立模型所用到的数据。

1.1 对VMS了解程度与是否改变出行路径的交叉分析

通过对问卷调查结果的整理分析，得出驾驶员对VMS了解程度以及是否改变出行路径的交叉分析统计结果，如图2。可以看出，对VMS越了解的驾驶者越倾向根据VMS提供的信息改变原定驾驶路线。

1.2 对VMS关注程度与是否改变出行路径的交叉分析

如图3，问卷调查的结果显示，对VMS越关注的驾驶者越倾向根据VMS提供的信息改变原定驾驶路线。

2 驾驶员路径选择模型的建立

2.1 广义线性模型

广义线性模型，就是经典线性回归模型的普遍化。经典线性回归模型假设因变量为一组自变量的线性方程，同时因变量为连续且正态分布的，可以写成：

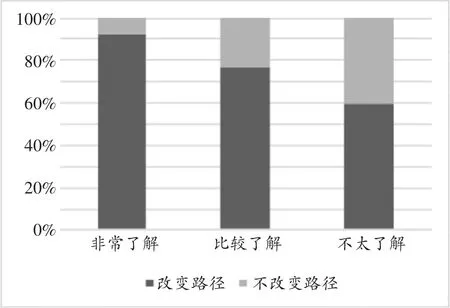
图2 不同VMS了解程度下的路径改变的意向

图3 不同VMS关注程度下的路径改变的意向

其中，y是连续因变量，xj是自变量，ε为假设正态分布的误差。因变量由两部分组成：系统性成分β0+βjxj，以及误差成分ε。参数β0被称为截距，即当所有自变量都为0时因变量的期望值。

这种线性回归模型发展自19世纪，随着人们需求的不断提升，线性回归的局限性也愈发凸显出来。比如，它假设因变量是连续的或者至少是准连续的，同时该连续变量需要满足正态分布。在1972年，Nelder和Wedderburn提出了广义线性模型（Generalized Linear Model，GLM），后来发展为应用于非正态因变量的回归模型。通过选择适当的连接函数，就可以使用广义线性模型对多种数据进行处理分析。

2.2 广义线性混合模型

标准广义线性模型假设样本是相互独立的，但是在很多情况下受访者数据间是存在关联性的，不满足这种要求。因此，广义线性模型进一步被拓展为广义线性混合模型（Generalized Linear Mixed Model，GLMM），即通过引入混合效应，在反应不同对象间的异质性，以及同一对象不同观测值间的相关性。

混合效应分为两种：固定效应和随机效应。对于固定效应，参数的含义是，自变量每变化一个单位，对应变量平均变化多少。对于随机效应，参数是服从正态分布的一个随机变量，也就是说对于两个不同的自变量的值，对应变量的影响不一定是相同的。广义线性混合模型可以表示如下：

其中，βj代表固定效应参数，zj是具有随机效应的协变量，vj代表随机效应参数。

在本次问卷调查中，我们关注的是驾驶者接收到VMS信息后是否改变路径的概率，因此采用logistic回归。logistic回归的标准连结函数为logit，即，其中π表示二元因变量的平均数或事件发生的概率。那么，利用logistic回归的广义线性混合模型就可以写成：

其中，Z代表具有随机效应协变量的设计矩阵，向量U代表随机效应。

2.3 影响因素的确定

对问卷进行分析，初步将驾驶者的性别、年龄、驾龄、车辆类型、VMS显示颜色、文字等确定为影响因素。性别、年龄、驾龄、车辆类型、快速路使用频率为哑变量，其中性别女性、最高年龄、最高驾龄、几乎不使用快速路以及使用其他类型的车辆为用于对比的变量。模型变量及含义如表2所示：

表2 模型变量及含义

2.4 模型估计

建立广义线性混合模型，如下所示：

利用SAS软件中的GLIMMIX过程进行参数求解，模型协方差参数估计如表3所示：

表3 模型协方差结果

在固定效应方面，本文选择概率为0.2作为筛选变量的标准，当p值小于0.2时，表明变量对结果的影响显著。本文之所以选择0.2作为筛选标准，是为了避免遗漏某些重要的自变量。模型参数结果如表4所示：

表4 模型参数结果

2.5 系数分析

（1）性别。性别Gender的系数为正，表明相比于女性，男性更倾向于改道。根据以往的出行行为研究来看，男性对于道路拥堵带来的延误更加敏感，因此会更倾向于改道。

（2）驾龄。驾龄DrvExp的系数均为正，而且系数有增大的趋势，表明随着驾龄的增长，改道的可能性变大。可能的原因是驾驶经验越丰富，对地面替换道路的情况越熟悉。在接收到道路拥堵延误信息后，能够通过改道减少对自己的影响。

（3）车辆类型。VclType1（私家车）与VclType2（单位用车）的系数为正，说明与单位用车相比，私家车的驾驶员更倾向于改道，可能是由于单位用车的油耗可以报销，从而对延误不敏感。VclType3（出租车）的系数为负，表明出租车的驾驶员倾向于不改道，可能是由于乘客付费且改道易引起乘客不满。

（4）高架使用频率。ExwUse的系数均为负，说明快速路使用频率越高，越倾向于不改道，而很少使用快速路的驾驶员更容易受到VMS的影响。

（5）图形板颜色。Color的系数为正，说明颜色是影响驾驶员路径选择的重要因素，红色所占比例越大，代表延误时间越长，驾驶员更加倾向改道。

（6）延误原因的文字描述在本调查中对并未对驾驶员产生重要影响，可能的原因是驾驶员在驾驶过程中并没有足够时间来阅读信息板的文字。

2.6 模型对比

为了验证广义线性混合模型在处理此类数据上的优势，本文将引入随机效应和不引入随机效应的两种模型运行的结果进行对比，如表5所示：

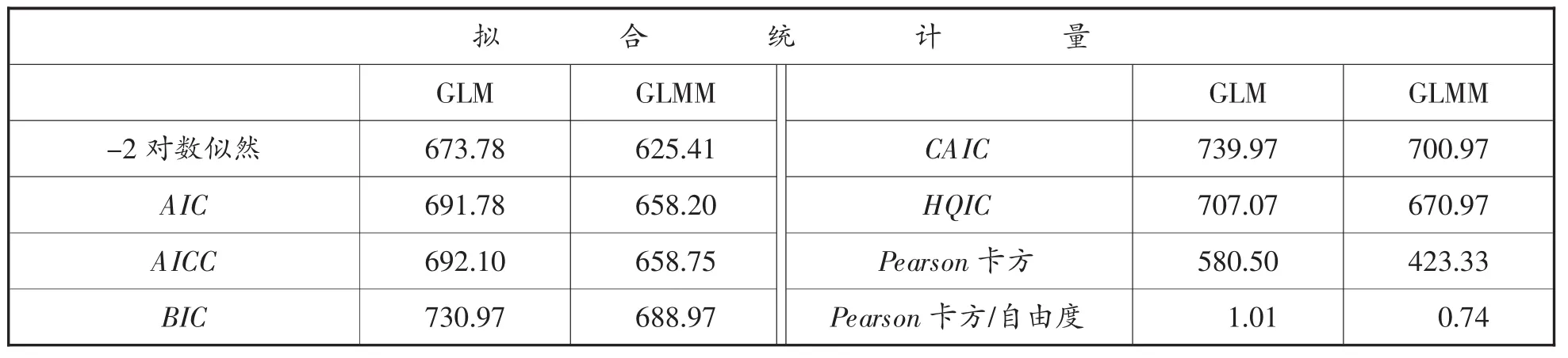
表5GLM和GLMM拟合统计量对比

其中，AIC、AICC、BIC、CAIC、HQIC均是非均衡重复测量指标，用来判断模型拟合程度，均是数值越小代表拟合结果越好。可以看到，GLMM下的指标均小于GLM，这表明在处理非均衡的调查数据时，广义线性混合模型比广义线性模型更具优势。GLMM的Pearson卡方／自由度小于1，也说明不存在过离散，拟合效果较好。

3 结论与建议

本文利用广义线性混合模型对驾驶员路径选择行为进行分析，并且通过与广义线性模型对比，可以看到加入混合效应会对模型拟合产生积极的影响，是分析此类数据更好的选择。

就政策建议而言，在建立VMS信息版的时候，应多考虑视觉因素，如颜色、图形等。同时各单位应完善车辆使用制度，避免带来不必要的油耗浪费。出租车公司应该积极引导驾驶员与乘客的进行有效沟通，提高乘客的体验感受。

[1]Papageorgiou M.Dynamic modeling，assignment，and route guidance in traffic networks[J].Transportation Research Part B Methodological，1990，24(6)：471-495.

[2]Said Mammar，Albert Messmer，Peder Jensen，et al.Automatic control of Variable Message Signs in Aalborg[J].Transportation Research Part C，1996，4(3)：131-150.

[3]Jianjun Wang，Qiong Wu.Study on Multi-Objective Optimization Model for VMS Layout on Expressways[J].Applied Mechanics and Materials，2013(361)：2012-2015.

[4]石小法，王炜，李文权.交通信息对交通网络的影响研究[J].系统工程学报，2001，16(3)：167-171.

[5]曾松，史春华，杨晓光.基于实验分析的驾驶员路线选择模式研究[J].公路交通科技，2002，19(4)：85-88.

[6]熊轶，黄海军，李志纯.交通信息系统作用下的随机用户均衡模型与演进[J].交通运输系统工程与信息，2003，3(3)：44-48.

[7]干宏程，孙立军，陈建阳，等.提供交通信息条件下的途中改道行为研究[J].同济大学学报（自然科学版），2006，34(11)：1484-1488.

[8]尚华艳，黄海军，高自友，等.基于元胞传输模型的实时交通信息设计[J].北京航空航天大学学报，2008，34(2)：234-238.

[9]干宏程，叶昕.行程时间波动性对路径选择影响的离散选择分析[J].交通运输系统工程与信息，2010，10(1)：140-144.

[10]朱冬辉，王珂英.广义线性混合模型在顾客满意度研究中的应用——基于某地区银行理财产品顾客满意度的分析[J].统计与信息论坛，2014，29(1)：94-99.

[11]（美）乔治·H.邓特曼，（加）何满镐.广义线性模型导论[M].林毓玲，译.上海：格致出版社，2012.

[12]詹姆斯·杰卡德.Logistic回归中的交互效应[M].上海：格致出版社，2014.

[13]弗雷德·C，潘佩尔.Logistic回归入门[M].上海：格致出版社，2015.

[14]瓦尼·布鲁雅.logit与probit：次序模型和多类别模型[M].上海：格致出版社，2012.

[15]费宇，陈飞，喻达雷，等.线性和广义线性混合模型及其统计诊断[M].北京：科学出版社，2016.