煤矿封闭火区渗透注浆过程中浆液扩散半径的影响因素分析及应用

陈 琛 王孟飞 屈英杰 刘振乾

(中国矿业大学(北京) 资源与安全工程学院，北京市海淀区，100083)

矿井火灾是矿山五大灾害之一，对矿工的健康和生态环境造成了严重的威胁。据统计资料显示，我国正在开采的煤层中，有大约80%为容易自燃煤层。目前我国矿井的主要防灭火方法有灌浆防灭火技术、均压防灭火技术等。其中，灌浆技术由于其成本低、工艺简单等优势，在我国得到了广泛的应用。通过灌浆，不仅可以充填采空区和煤岩中的裂隙，还可以对煤体起到一定的降温作用，使防灭火效果更好。但在以往的灌浆过程中，只突出了一个“灌”字，浪费了大量的灌浆材料和人力资源，同时也影响了矿井的安全生产。浆液扩散半径表征的是以灌浆钻孔为原点的浆液充填范围的大小，决定着灌浆钻孔的布置、浆液消耗量等其他参数。因此，良好的灌浆技术，依赖于对影响扩散半径的因素进行深入研究。朱俞仿基于平板裂隙灌浆模型，考虑了裂隙倾角对浆液扩散半径的影响；韩磊等进行了大坝灌浆过程模拟，得出渗透系数和孔隙度对扩散半径均有影响。但是现有研究均是对影响扩散半径的某一因素进行分析，与实际工程应用中多影响因素相互作用不相适应。因此，本文根据浆液扩散半径计算的基础理论，对多影响因素相互关联下的扩散半径进行了数值计算，以期获得土水比、灌浆压力、灌浆钻孔半径、裂隙度等对浆液扩散半径的影响，并提出了具体的灌浆技术参数，为灭火实践提供理论参考。

1 浆液扩散半径计算的理论基础

在灌浆过程中，浆液的扩散半径在很大程度上受浆液粘度的影响。粘度不同，计算出的扩散半径差别很大。在计算扩散半径的过程中，可以分为在注浆过程中浆液粘度不变或者变化很小和浆液粘度显著变化两种情况。

1.1 注浆过程中浆液粘度不变或变化很小

根据平板注浆模拟试验台，并应用牛顿流体内摩擦阻力定律，在裂隙中注浆浆液扩散半径计算公式为：

(1)

式中：R——浆液扩散半径，cm；

t——注浆时间，s；

P2——注浆孔内压力，Pa；

P1——受注裂缝内地下水压力，Pa；

b——裂缝宽度，cm；

μ——浆液粘度，Pa·s；

r——注浆孔半径，cm。

式(1)的计算基础为注浆过程中浆液是牛顿流体，流动符合牛顿内摩擦定律。但事实上浆液在流动的过程中不止受到内摩擦力，还受到流体本身剪应力的影响，并且其粘度也会随着时间发生变化。因此，由式(1)计算出的浆液扩散半径略大于实际值。为了消除计算值偏大的影响，在式(1)的基础上乘上一个修正系数σ(0<σ<1)；利用灌浆进行防灭火时，忽略存在地下水的影响，因此式(1)中的P1为0 Pa。综合以上两个假设，式(1)变为：

(2)

1.2 注浆过程中浆液粘度显著变化

研究表明，在灌浆灭火工程中，对于浆液材料粘度变化大的液体而言，浆液粘度对时间变化的拟合方程为：

μ(t)=KeAt

(3)

式中：μ——浆液的动力粘度，Pa·s；

K，A——待定常数，由浆液性质决定。

结合式(1)和式(3)，可得出粘度显著变化时浆液注浆的扩散半径的理论计算公式：

(4)

2 不同因素对浆液扩散半径的影响分析

为了分析灌浆过程中，扩散半径与土水比、灌浆压力、钻孔半径和裂隙度的关系，必须对不同条件下的浆液扩散半径进行计算并分析结果。笔者以平板注浆模拟结果为模型，根据式(2)和式(4)编制钻孔灌浆计算程序进行数值计算，并采取控制变量法对各因素对扩散半径的影响进行逐一计算。

2.1 浆液土水比对浆液扩散半径的影响

当灌浆钻孔半径为50 mm，裂隙度为50 mm，灌浆时间为10 min，灌浆压力分别为0.5 MPa、1 MPa、2 MPa时，得到不同土水比下的浆液扩散半径趋势图，如图1所示。

图1 不同土水比与扩散半径对应关系图

由图1可以看出，当灌浆时间、裂隙度等参数固定不变时，不同的灌浆压力下，扩散半径和土水比的关系近似为一条直线，但是其斜率较小。以压力为1 MPa时为例，土水比由1∶2减小到1∶4时，扩散半径由56.8199 m增加到65.8121 m，土水比降低一半，扩散半径仅增加0.16倍左右。这说明扩散半径虽然随着土水比的减小而呈增加趋势，但是增加得较为缓慢。

一般情况下，水土比大，浆液稀，浆液粘度小，易于输送，输送距离长，浆液扩散半径大，但容易造成水土分离和跑浆，不能有效地进行充填，浆液无法把碎煤块包裹，达不到预防灭火目的；水土比小，浆液粘度大，流动性差，输送距离短，容易造成管道的堵塞和过度磨损，浆液的扩散半径小，增加灌浆成本。

2.2 灌浆压力对浆液扩散半径的影响

当灌浆钻孔半径为50 mm，裂隙度为50 mm，灌浆时间为10 min，土水比分别为1∶2、1∶3、1∶4、1∶5时，得到不同灌浆压力的浆液扩散半径趋势图，如图2所示。由图2可以看出，随着灌浆压力的增大，浆液扩散半径也不断增大。以土水比为1∶4时为例，灌浆压力为1 MPa所对应的扩散半径是灌浆压力为0.5 MPa时的1.37倍，灌浆压力为2 MPa所对应的扩散半径是灌浆压力为0.5 MPa时的1.87倍。很显然，灌浆压力对扩散半径的影响较浆液土水比更显著。

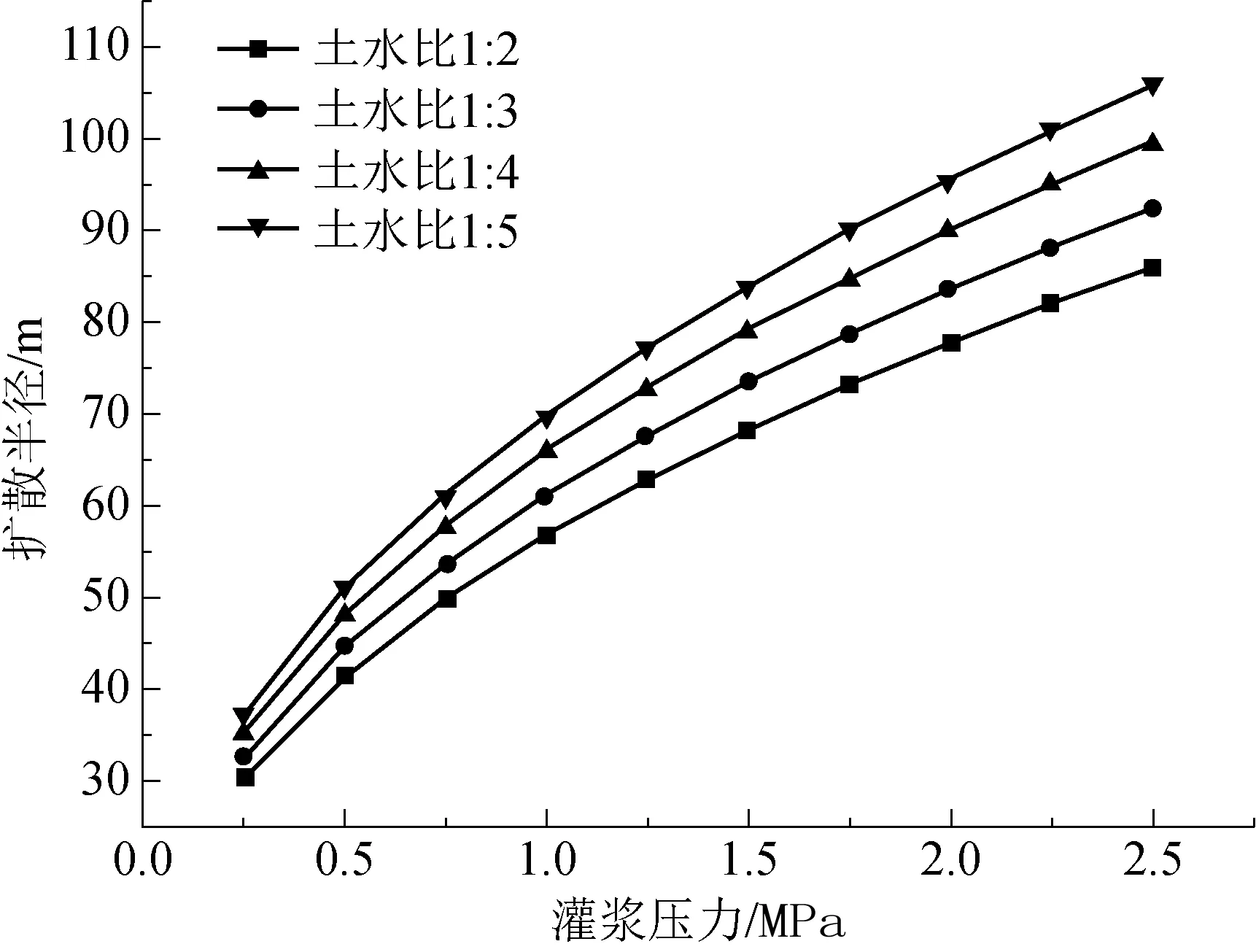
图2 不同灌浆压力与扩散半径对应关系图

随着灌浆压力的增大，扩散半径也会增大，这样钻孔的数目便会减少，会大大地降低防灭火灌浆工程的工程量。但是，灌浆压力也不宜过大，不然可能会出现跑浆等现象，并且摧毁一些隔离煤柱和密闭墙，严重影响矿井的安全生产。

2.3 钻孔半径对浆液扩散半径的影响

当灌浆压力为1 MPa，裂隙度为50 mm，灌浆时间为10 min，土水比为1∶2、1∶3、1∶4时，得到不同钻孔半径下的浆液扩散半径趋势图，如图3所示。

图3 不同钻孔半径与扩散半径对应关系图

由图3可以看出，当灌浆时间、裂隙度等灌浆参数不变时，扩散半径和钻孔半径的关系近似为一条直线，斜率为正值且该条线斜率很小。这说明，扩散半径随着钻孔半径的增加而慢增加，并且增加得很缓慢。以土水比为1∶4时为例，钻孔半径由2 cm增加到8 cm，扩散半径仅由60.728 m增加到了68.365 m，仅增加了原来的0.12倍。由此可见，钻孔半径对扩散半径的影响甚小，在实际灌浆防灭火工程中不应该通过过大的钻孔半径来提高扩散半径，这样会大大地增加钻孔的工程量，而取得的效果甚微。

2.4 裂隙度对浆液扩散半径的影响

当灌浆压力为2 MPa，钻孔半径为50 mm，灌浆时间为10 min，土水比分别为1∶3、1∶4时，得到不同裂隙度下的浆液扩散半径，并绘制出不同土水比下不同裂隙度与浆液扩散半径的关系图，如图4所示。

图4 不同裂隙度与扩散半径对应关系图

由图4可以看出，当灌浆时间、灌浆压力、钻孔半径等参数不变时，扩散半径和裂隙度的关系近似为一条直线，并且斜率很大。这说明，当裂隙度增大时，扩散半径也会增大，且增大幅度较大，即裂隙度对扩散半径的影响是很大的。以土水比为1∶4时为例，裂隙度由2 cm增加到8 cm时，扩散半径便由原来的59.4939 m增加到111.3815 m，整整增加了0.87倍。很明显，裂隙度对扩散半径的影响要比钻孔半径对扩散半径的影响大得多。但是，裂隙度主要取决于煤层顶板岩性、分层厚度、岩石强度以及冒矸压实程度等，该值很难人为改变。

综合图1～图4可以看出，土水比、灌浆压力、钻孔半径、裂隙度均对浆液扩散半径有一定的影响，但是影响程度大小不一。其中，灌浆压力、钻孔半径和裂隙度都和浆液扩散半径是正比关系，浆液扩散半径随着它们的增大而有不同程度的增大。浆液土水比和扩散半径是反比关系，浆液扩散半径随着土水比的增大而减小，这主要是因为随着土水比的增大，浆液中的水分逐渐减少，使得浆液粘度增加，从而使得扩散半径有所减小。从图中的斜率来看，裂隙度对浆液扩散半径的影响最大，灌浆压力次之，浆液土水比再次之，钻孔半径对扩散半径的影响最小。

3 实践应用

山西雁儿崖煤矿414盘区14-2#煤层厚度2.52～2.58 m，平均煤层厚度2.5 m。盘区全长1000 m，盘区内地质构造复杂，工作面走向长在200～1000 m之间，于1995—2000年采毕。该矿救护队巡巷时发现414盘区51412、51414巷永久密闭附近温度异常，最高温度78℃。矿通风队立即在51412、51414巷口重新构筑了两道防火密闭。14-2#煤层因开采面积大，开采年限长，火区位置以及上覆11#煤层遭小窑破坏情况现已无法确定，故不能采用惰化和均压灭火技术灭火。通过分析，认为采用灌浆系统灭火方法简单，见效快，同时414盘区上覆山头黄土覆盖较厚，土源丰富，因此利用静压水方便的优点，便于灌浆灭火。

因此，决定采用前述理论与数值分析结论，应用地面灌浆防灭火成果对该区域进行灌浆灭火。根据对浆液扩散范围的研究，顶板为砂质岩时泥浆的流动距离在70 m以上，因此本盘区设计的泥浆流动距离为70 m。414盘区全长1000 m，设计灌浆面积为S=1000×70=70000 m2；经计算灌浆所需土量为31500 m3；泥浆的水土比取3∶1，需水量为113400 m3；总灌浆量为164660 m3。灌浆120 d，灌浆量为1372.2 m3/d，每天灌注21 h，灌浆量为65.34 m3/h，每孔灌浆量为13722 m3。

该矿通过修建灌浆系统，并向采空区密闭灌浆孔进行堵漏隔离灌浆，灌浆顺序由盘区两侧向盘区中央采空区处依次灌浆。在灌浆施工过程中及灌浆结束后，对14-2#煤层414盘区采空区火区每4 d进行温度和有害气体浓度监测，检测结果表明，灭火工程结束两个月后，孔内温度己接近常温，CO等气体浓度已低于《煤矿安全规程》所规定的允许气体浓度，达到了规定的火区熄灭标准。

4 结论

本文利用钻孔灌浆计算程序进行数值计算，对影响浆液扩散半径的因素进行了分析，得出影响浆液扩散半径的因素主要有注浆压力、钻孔半径、裂隙度和浆液土水比，并且裂隙度对浆液扩散半径的影响最大，灌浆压力次之，浆液土水比再次之，钻孔半径对扩散半径的影响最小。通过现场应用，证实了理论和数值分析的效果。

参考文献：

[1] 曹胜.煤矿井下封闭火区气体生成及变化规律试验研究[D].太原理工大学,2017

[2] 秦鹏飞.砂砾石土渗透注浆浆液扩散规律及扩散半径影响因素试验研究[J].中国水利水电科学研究院学报,2015(5)

[3] 张纯波.鑫发煤矿灌浆防灭火技术[J].现代矿业,2014(5)

[4] 李振钢.砂砾层渗透注浆机理研究与工程应用[D].中南大学,2009

[5] 朱俞仿.裂隙倾角对灌浆扩散半径的影响分析[J].中国矿山工程,2014(2)

[6] 韩磊,陈建生,陈亮.帷幕灌浆扩散半径及数值模拟的研究[J].岩土力学,2012(7)

[7] 刘嘉材.裂隙珠江扩散半径的研究[A].水利水电科学院研究论文集[C].北京：水利出版社，1982

[8] 岩土注浆理论与工程实践协作组.岩土注浆理论与工程实例[M].北京：科学出版社，2001