淮南矿区地表下沉系数主控因素分析与回归计算
郭文砚 胡炳南 范明宇 栾合冰 李仕博
(1.中国矿业大学(北京) 资源与安全工程学院,北京市海淀区,100083;2.煤炭科学研究总院,北京市朝阳区,100013;3.煤炭开采水资源保护与利用国家重点实验室,北京市朝阳区,100011;4.清华大学水沙科学与水利水电工程国家重点实验室,北京市海淀区,100084)
地表下沉系数是开采沉陷地表移动与变形预计的重要参数,其取值的准确性直接影响到地表移动与变形预计结果的准度。影响下沉系数的因素很复杂,理论研究难以全面考虑各种因素的影响,而大量建立地表移动观测站实测下沉系数又耗费大量的人力、财力,且时间周期较长,不能满足煤矿快速生产的需要。国内学者对下沉系数预测方法已做了大量研究。邹友峰利用相似理论中的方程分析法,结合观测实例,推导出下沉系数的计算公式。刘三枝等运用模糊聚类分析方法对123个观测站进行计算、分类和分析,得出不同类群情况下的下沉系数的取值范围和计算公式。郭文兵等采用人工神经网络方法建立地表下沉系数的计算模型,运用实地观测资料作为学习训练样本对下沉系数进行预测。王拂晓等将遗传算法和广义回归神经网络方法进行融合,建立了基于GA-GRNN的地表下沉系数预测模型。这些预测方法都有一定的适用性。灰色关联分析法是一种简单实用的描述多因素之间相关程度的统计方法,回归分析法是一种重要的预测方法,在分析多因素模型时,更加方便快捷。本文通过对淮南矿区研究区域影响下沉系数的地质与采矿因素进行分析,利用灰色关联法分析出影响下沉系数的主控因素,通过对11组下沉系数及其相关影响因素的实测数据进行回归分析,得出下沉系数的线性回归预测公式及中误差,并给出公式适用的条件,使预测结果更准确,可为淮南矿区煤矿开采和类似矿区下沉系数计算提供参考。
1 淮南矿区观测站位置及下沉系数影响因素分析
1.1 观测站位置
本次收集了淮南矿区11组地面观测站数据,见表1,共涉及顾桥矿(3组)、丁集矿(1组)、潘二矿(2组)、潘三矿(2组)、潘四矿(2组)和谢一矿(1组)。淮南矿区煤矿分布如图1所示,观测站主要分布在淮南矿区中部偏北。
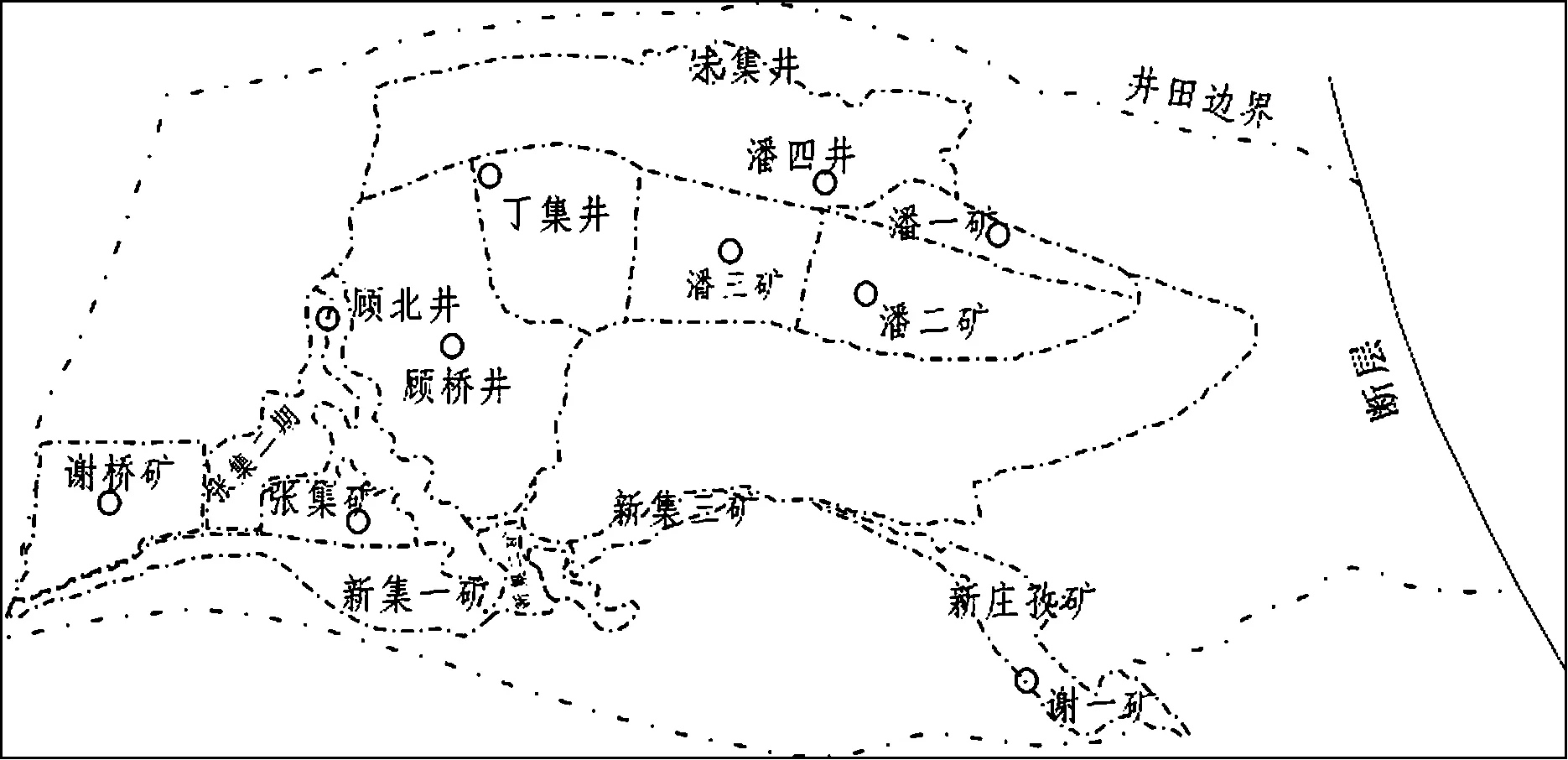
图1 淮南矿区煤矿分布图

表1 观测站数据表
注:Wd-基岩岩性程度系数;M-采厚;α-煤层倾角;h-松散层厚度;H0-平均采深;Vt-推进速度
1.2 下沉系数的影响因素分析
通过大量实测资料与理论研究,下沉系数主要与矿区的地质和采矿条件相关,结合淮南矿区条件,主要有以下因素:
(1)基岩岩性程度系数Wd。基岩岩性对煤层开采后上方地表的下沉值有重要影响。研究表明,基岩岩性越坚硬,下沉系数越小,基岩岩性越软弱,下沉系数越大。淮南矿区煤系地层以二叠系为主,基岩以泥类岩与砂类岩为主,收集到各类岩性占比数据,借鉴文献中P系数法,采用基岩岩性程度系数Wd来反映基岩岩性,Wd计算公式如下:
(1)
式中:rai——各类岩性占比,ra1+ra2+…+ran=1;
Qi——岩性评价系数。
综合观测站工作面顶板泥类岩、砂类岩占比数据和煤矿区钻孔覆岩岩性条件,观测站工作面基岩岩性相对中硬。
将观测站基岩岩性程度系数Wd计算值与下沉系数q进行拟合,结果如图2所示。由图2可以看出,研究区域系数Wd值在0.4~0.6之间,Wd值越大,泥岩占比越大,岩性越偏软弱。下沉系数与覆岩岩性有一定相关性,随着岩性变弱,下沉系数逐渐变大。由于淮南矿区松散层厚度大,基岩厚度小,基岩的岩性越软弱,在厚松散层作用下易发生较大移动与变形,使下沉量增大。
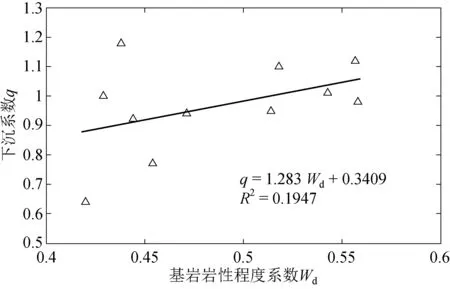
图2 基岩岩性程度系数与下沉系数线性关系图
(2)采厚M。在充分采动情况下,开采厚度越大,采动程度相对越剧烈,地表最大下沉值会增大。将观测站工作面煤层采厚M与下沉系数q进行拟合,结果如图3所示。由图3可以看出,研究区域的下沉系数与采厚无相关性,可能是因为研究区域采厚变化范围小,数值较集中,对下沉系数的影响较小。
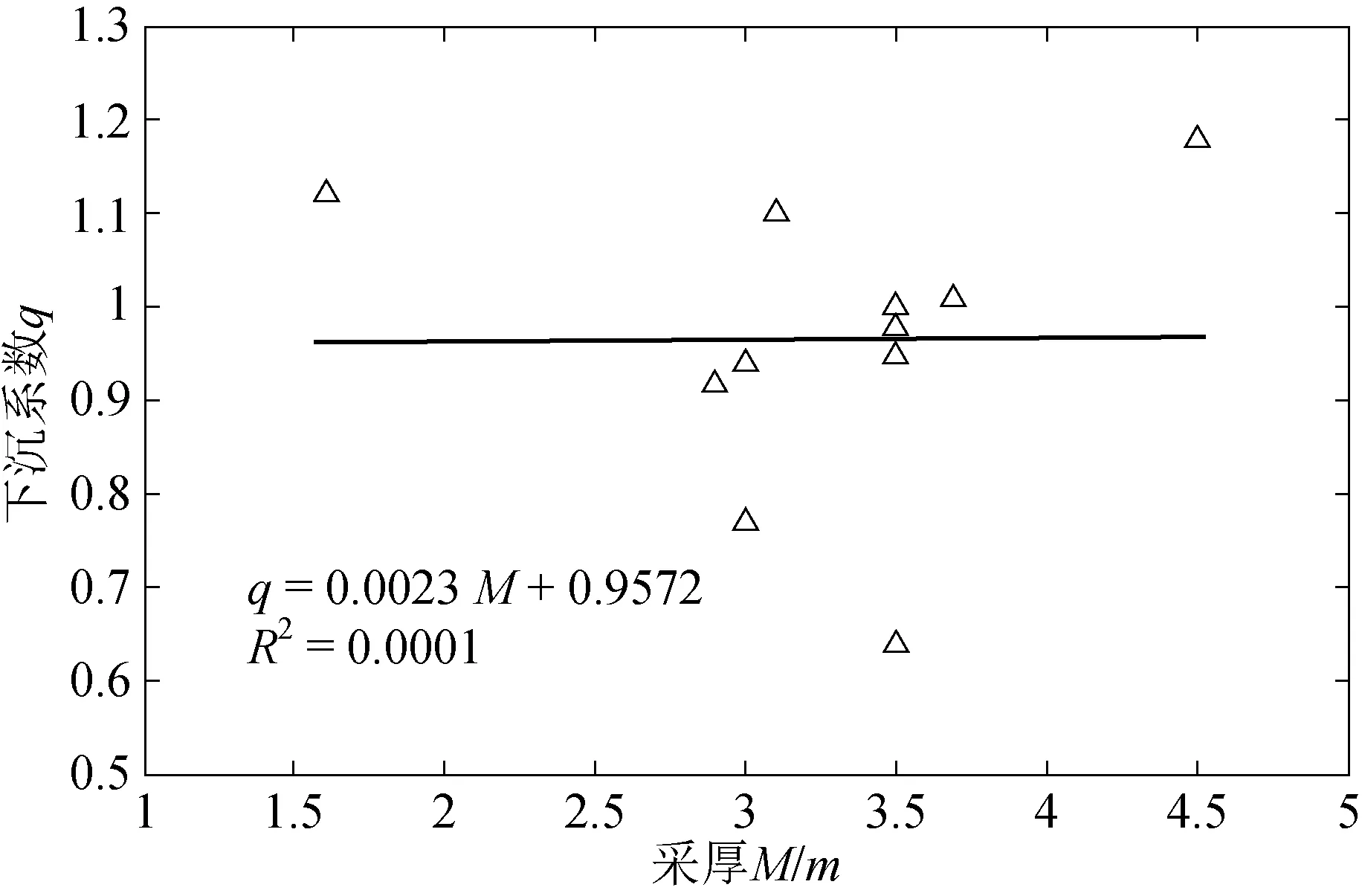
图3 采厚与下沉系数线性关系图
(3)煤层倾角α。煤层倾角的变化对上覆岩层的移动与破坏形式及地表沉陷盆地形态有很大的影响。将观测站工作面煤层倾角α值与下沉系数q进行拟合,结果如图4所示。由图4可以看出,研究区域的下沉系数随倾角的增大有减小趋势,下沉系数与倾角有一定相关性。
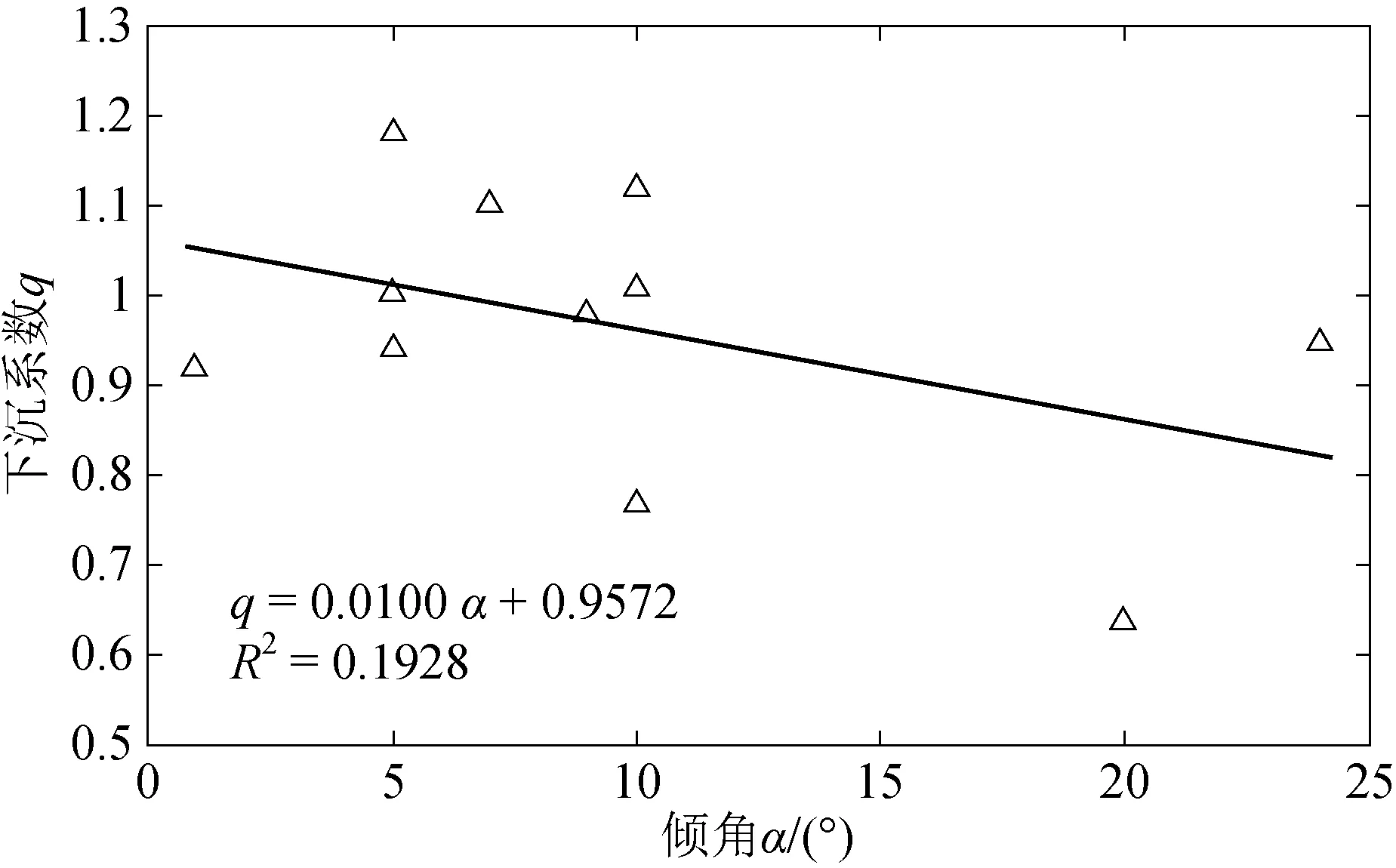
图4 倾角与下沉系数线性关系图
(4)松散层厚度占比h/H0。研究表明,我国的华东、华中、华北等地区地层上部覆层含有巨厚的松散层,煤层开采后地表沉陷显现出特殊的规律,下沉系数较大,接近1或者大于1。一般松散层厚度越大,下沉系数越大,而开采深度越大,煤层开采对地表产生的扰动越小,下沉系数越小,因此以松散层厚度h与平均采深H0的比值来表示松散层厚度与基岩厚度对下沉系数的影响。将松散层厚度占比h/H0与下沉系数q进行拟合,结果如图5所示。由图5可以看出,研究区域松散层厚度占比的值集中在0.5~0.9之间,松散层厚度大于基岩厚度,松散层厚度均值为346 m,而下沉系数均值为0.96,下沉系数随松散层厚度占比的增大而增大,下沉系数与松散层厚度占比的线性相关性相对较好,与研究结果相符。
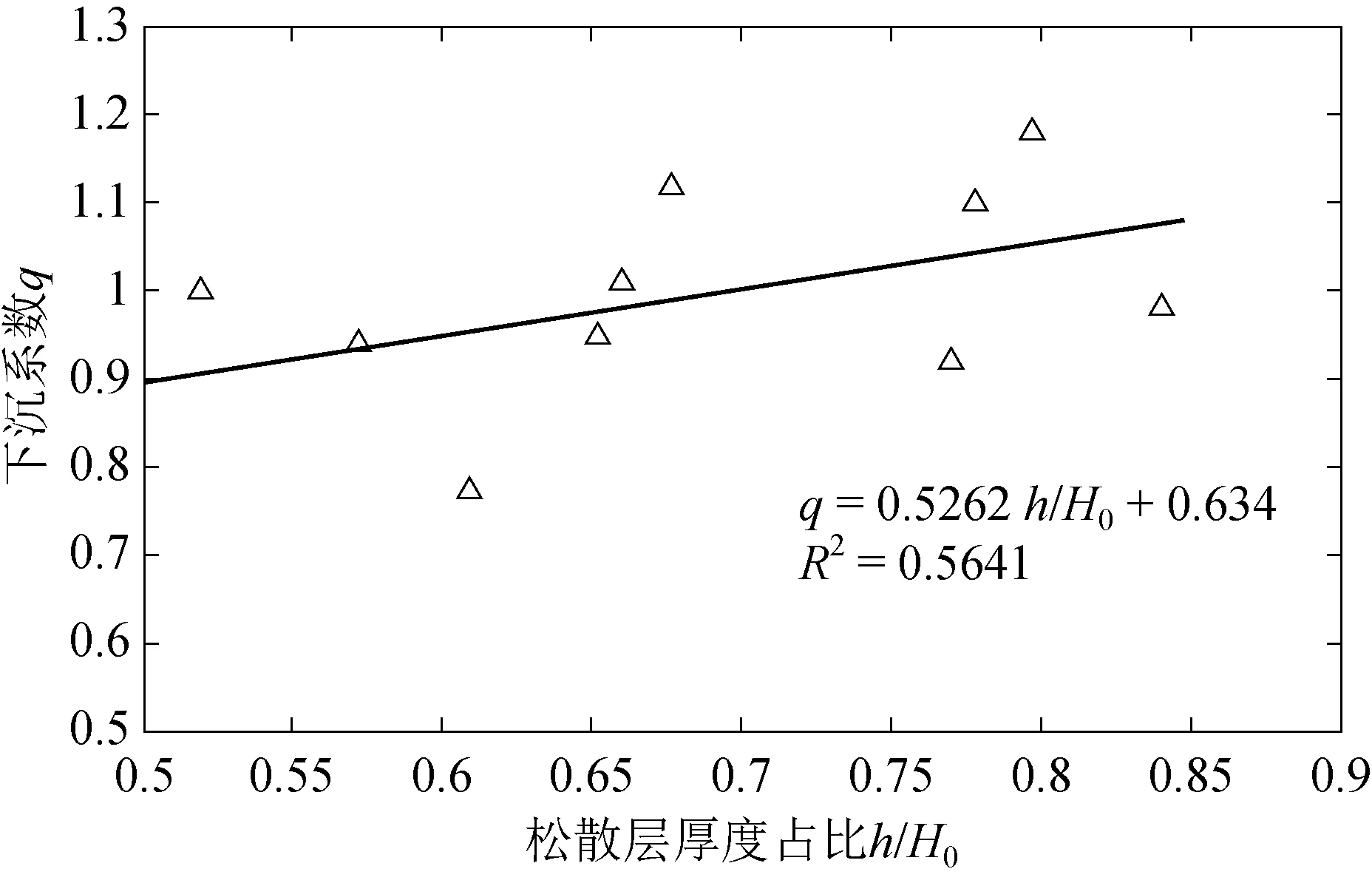
图5 松散层厚度占比与下沉系数线性关系图
(5)推进速度Vt。在采动过程中,工作面推进速度的快慢,对于地表沉陷及土体的应力分布均有较大影响。一般推进速度越快,地表动态变形值小,下沉值小,下沉系数减小。将研究区域内工作面推进速度Vt与下沉系数q进行拟合,结果如图6所示。由图6可以看出,下沉系数与推进速度的相关性很差,且下沉系数随推进速度的增大有增大趋势,与理论分析不符,分析推进速度可能受其他因素的影响从而对下沉系数的影响程度较小。
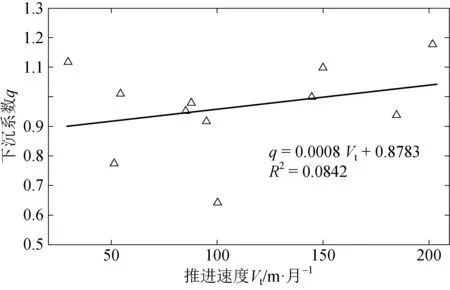
图6 推进速度与下沉系数线性关系图
(6)采煤方法与顶板管理方法。本次收集的11组观测站,采煤方法均为走向长壁综采一次采全高,顶板管理方法均为全部垮落法。对特殊条带开采法、房柱式采煤法等暂不作讨论。
(7)重复采动。初次采动会使上覆岩层破裂、离层进而软化,重复采动会引起岩体的碎胀量减小,破裂岩体内的空隙闭合,使地表变形增大,导致初次采动的下沉系数会增大。本次观测站工作面无重复采动情况。
2 淮南矿区下沉系数主控因素分析
2.1 灰色关联分析法
灰色关联度分析法是一种多因素统计分析方法,它是以各因素的样本数据为依据用灰色关联度来描述因素间关系的强弱、大小和次序,若样本数据反映出的两因素变化的态势基本一致,则它们之间的关联度较大;反之,关联度较小。通过灰色关联分析法可以分析出下沉系数的主控因素,可更好地用于预测开采地表移动特征。
国家电网公司服务乡村振兴建设,推进“全能型”乡镇供电所建设科技创新,加快推进数字化、信息化发展,激发创新活力,培育新业态和创新服务模式,同时,依靠数字化、信息化技术的发展有力推进了乡镇供电所建设的科技创新与管理创新,改变传统产业的生产方式、管理模式和企业组织结构,企业组织结构模式日益由以分工为主导思想的组织结构模式,演变为以集成管理为主导思想的组织结构模式,工程设计行业数字化、信息化、集约化的发展趋势,将对国家电网公司服务乡村振兴建设发展带来战略性和全局性的影响。
2.2 主控因素分析
将下沉系数视为目标因素,基岩软硬程度系数、采厚、煤层倾角、松散层厚度占比、推进速度为子因素。利用Matlab软件,通过构建初始数据矩阵—初值法数据无量纲化—总极差法计算绝对差值矩阵—计算关联系数矩阵—计算关联度,取分辨系数为0.3(分辨系数取值越小,关联系数间的差异越大,分辨能力越强,通常情况下取0.1~0.5区间为宜),计算研究区域子因素与目标因素的灰色关联度为:
=[0.8742,0.7619,0.6149,0.8567,0.7467]
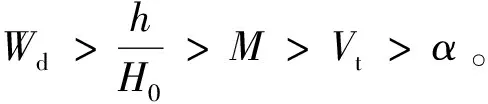
3 下沉系数回归计算
3.1 多元线性回归分析
多元线性回归模型的一般形式为:
y=β0+β1x1+β2x2+…+βmxm+ε
(2)
式中:β0——常数项;
β1,β2,…,βm——回归系数;
ε——残差。
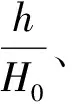
(3)
利用Matlab拟合工具箱对研究区域数据进行线性回归,得到下沉系数回归预测公式:
(4)
式(4)的相关系数r2=0.7095,|r|=0.842,说明模型变量之间有一定相关性,但检验统计量F偏小,说明模型回归检验不显著,这是由于数据样本较少导致回归效果不太明显。
3.2 回归公式与预测误差分析
式(4)中下沉系数与各因素(除推进速度因素)之间的变化趋势是符合一般研究规律的,而推进速度因素与下沉系数的变化趋势与上文分析不符,可能是受其他因素的影响较大,因此去掉推进速度因素,得到新的回归公式如下,计算结果误差率见表2。
(5)
由于基岩软硬程度系数和松散层厚度占比因素是下沉系数的主控因素,为简化下沉系数计算,用主控因素进行回归,得到下式,计算结果误差率见表2。
(6)

表2 下沉系数计算误差值
由表2可以看出,式(5)计算的最大误差为19.9%,最小误差为1.3%,误差均值8.05%,误差值小于均值的有5组,下沉系数的中误差为0.093;式(6)计算的最大误差为23.0%,最小误差为0.7%,误差均值8.26%,误差值小于均值的有5组,下沉系数的中误差为0.097,式(5)与式(6)的预测结果相近。考虑回归预测公式的影响因素较多,预测值因某一因素波动而变化,多受因素波动的中间段数值影响较大,由于基岩软硬程度系数和松散层厚度占比因素是下沉系数的主控因素,这两个因素对预测下沉系数的影响较大,基岩软硬程度系数的变化范围为0.420~0.558,松散层厚度占比的变化范围为0.519~0.840,即这两个值越靠近中间段,预测值越准确。考虑引入中误差,当基岩软硬程度系数数值小于0.450且松散层厚度占比小于0.60时,减去0.10的中误差;当基岩软硬程度系数数值大于0.550且松散层厚度占比大于0.80时,增加0.10的中误差。表2中的第2组、10组数据符合条件,可增减中误差,提高公式的预测精度。考虑中误差后,可使误差均值降为6.42%,因此用回归公式预测下沉系数是合理可行的。
研究区域以覆岩岩性、松散层厚度占比为主控因素,当前该回归预测公式主要适用于覆岩岩性中硬、松散层厚度占比大于0.5的矿区,回归公式有一定的适用性,可为淮南矿区煤矿开采和华东、华中、华北等类似厚松散层地区下沉系数计算提供参考。当前数据样本较少,若后期收集到更多数据,可通过类似步骤分析和回归新的预测公式。
4 结论
(1)通过淮南矿区研究区域实测下沉系数影响因素的灰色理论关联分析,基岩软硬程度系数、松散层厚度占比因素对下沉系数影响较大,为主控因素,采厚和推进速度因素的影响次之,倾角因素的影响最小。
(2)结合灰色理论关联分析,对研究区域11组数据进行回归分析,得到下沉系数与基岩软硬程度系数和松散层厚度占比因素的线性回归预测公式。并考虑中误差,当基岩软硬程度系数数值小于0.450且松散层厚度占比小于0.60时,减去0.10的中误差;当基岩软硬程度系数数值大于0.550且松散层厚度占比大于0.80时,增加0.10的中误差。11组数据的误差均值为6.42%,7组误差值小于均值,回归公式预测下沉系数是合理可行的。
参考文献:
[1] 张广伟,李凤明,李树志等.基于岩体破裂规律的下沉系数变化[J].煤炭学报,2013(6)
[2] 邹友峰.地表下沉系数计算方法研究[J].岩土工程学报,1997(3)
[3] 刘三枝,胡贤润.地表下沉系数的模糊聚类分析[J].南京建筑工程学院学报,2001(2)
[4] 郭文兵,邓喀中,邹友峰.地表下沉系数计算的人工神经网络方法研究[J].岩土工程学报,2003(2)
[5] 王拂晓,谭志祥,邓喀中.基于GA-GRNN的地表下沉系数预测方法研究[J].煤炭工程,2014(7)
[6] 何国清,杨伦,凌赓娣等.矿山开采沉陷学[M].徐州:中国矿业大学出版社,1994
[7] 阿维尔申.煤矿地下开采时的岩层移动[M].北京:煤炭工业出版社,1995
[8] 郭文兵,刘义新.深部条带开采下沉系数与采厚关系的数值模拟[J].河南理工大学学报(自然科学版),2007(3)
[9] 邹友峰,邓喀中,马伟民.矿山开采沉陷工程[M].徐州:中国矿业大学出版社,2003
[10] 国家煤炭局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[M].北京:煤炭工业出版社,2000
[11] 李德海,许国胜,余华中.厚松散层煤层开采地表动态移动变形特征研究[J].煤炭科学技术,2014(7)
[12] 陈俊杰,邹友峰,郭文兵.厚松散层下下沉系数与采动程度关系研究[J].采矿与安全工程学报,2012(2)
[13] 滕永海,刘克功.五阳煤矿高强度开采条件下地表移动规律的研究[J].煤炭科学技术,2002(4)
[14] 王悦汉,邓喀中,张冬至等.重复采动条件下覆岩下沉特性的研究[J].煤炭学报,1998(5)

