复变函数与积分变换的教学体验

□文 重庆师范大学数学学院 曾春娜 柏仕坤

重庆交通大学数学与统计学院 胡 进

复变函数与积分变换是高等数学的后续课程，在电气工程、通信与控制、信号分析与图像处理、流体力学等众多领域有着广泛的应用，是工科教育教学体系中重要的基础课程。本课程在培养学生抽象思维能力、逻辑推理能力、空间想象能力和科学计算能力等方面有着重要的作用，也为学生后续学习相关专业课奠定了重要的理论基础。

我们在多年的教学中发现，由于该课程理论性和逻辑性强，而学生普遍存在“重计算，轻理论”的情况，搞不清楚各章节及知识点之间的关系，再加之学生重视程度不够，因此常常反映课程难以理解。另一方面，教师在授课过程中往往存在“重理论，轻应用”的倾向，大量时间用于定理的证明，而忽视了在实际问题中的应用，再加上授课形式单一，授课内容一成不变，导致学生难以充分掌握这门课程的知识与方法。我们多年从事复变函数与积分变换的教学工作，总结了如下一些该课程的教学经验和方法，现做一简单介绍。

一、类比/对比教学法

复变函数与积分变换作为高等数学的后续课程，在课程体系和知识结构方面与高等数学有很多相似之处，也有一些明显差异。我们在教学过程中，从复变函数与高等数学的课程体系入手，对两门课程的知识点逐一进行比较，找到二者的异同点。这样不仅对复变函数与积分变换整体的知识体系有了更加清晰的认识，而且对其知识点也有更加透彻的掌握。

例如，我们会在课程的开始阶段将高等数学和复变函数的整体框架作对比，发现两门课程研究的主要内容都是函数、极限、连续、微分、积分、级数。进一步，在学习的过程中我们会发现函数，极限，连续这三部分内容在复变函数中所占篇幅很少，主要原因是其与高等数学中相应部分区别不大。而微分、积分部分差别就比较大，因此篇幅比重也比较大；微分部分复变函数中解析的概念是高等数学所没有的，有很多非常独特的性质，而积分部分复变函数侧重研究的是围线积分。此外，将积分与复级数结合起来，还得到了留数这个高等数学里没有的概念。通过这些比较，学生可以对复变函数所学知识点有比较清晰的认识。

又比如，在学习复积分时，我们有两种方式来理解复积分的概念。一种方式是将函数看成复变量z的函数，此时积分可以看成是高等数学中一元函数定积分的形式；另一种方式是将函数拆成实部和虚部，相应的积分也拆成实部和虚部，此时可以得到积分的实部和虚部分别是两个高等数学中的第二型曲线积分。后一种方式使我们明白复积分的本质是两个第二型曲线积分，在证明Cauchy积分定理的时候有非常重要的作用；而前一种方式则可以帮助我们计算复积分，特别是利用参数方程计算复积分。

通过类比和对比，学生可以更好地理解复变函数中的理论，加深对概念的理解，简化对理论的阐述，化繁为简。

二、利用思维导图，帮助学生搞清知识点之间的联系

复变函数与积分变换中概念和定理比较多，学生往往搞不清知识点之间的联系，也搞不清为什么研究这些知识点。为了帮助学生加深对概念的理解和记忆，我们引入了思维导图这个图形化思维的工具，利用节点和节点间的关联构造了知识点的网络，利用图形形象化的帮助学生理解知识点之间的联系。

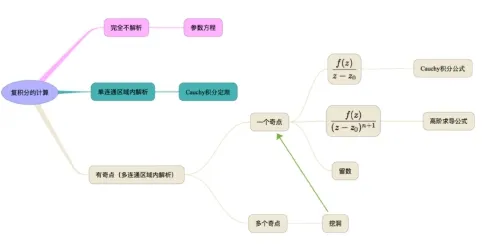
如上图就是我们总结的第三章关于复积分计算的思维导图。图中总结了不同情况下计算复积分的方法，特别是有奇点的情况下，从一个奇点，到多个奇点，一个奇点又分为不同的情况，逐渐深入。通过上述思维导图，学生可以对复积分这一部分有更清晰的认识，对为什么复积分要这样研究以及知识点前后之间的关联理解的更加透彻。由此可见，思维导图可以帮助学生将繁杂凌乱的知识点整合成一个整体，发现知识点之间的关联，并加以归纳整理，形成一个知识结构系统，从整体上把握相关知识。

三、将数学史融入教学，提高学习兴趣

复变函数与积分变换这门课程理论性比较强，学生学习起来感觉枯燥，因此如何调动学生积极性就非常重要。我们将数学史融入教学之中，活跃了课堂气氛，调动了学生的积极性，大大提高了学习兴趣。如在复变函数与积分变换的绪论中，我们从复数的发现入手，介绍整个复变函数的发展史，讲述了意大利数学家卡尔达诺是如何第一次发现了复数却因为不知道复数的意义而被很多人所误解，后来欧拉发现了欧拉公式，高斯和汉密尔顿将复数表示成实部和虚部的形式，复数才逐渐为人们所理解，“复变函数”这门一数学分支才得以顺利地建立和发展。在讲述这些数学故事时，我们会介绍卡尔达诺所在时期的数学发展情况，介绍大数学家欧拉和高斯的生平故事，介绍欧拉公式的重要性。学生对这些数学轶事很感兴趣，通过这些故事不仅调动了学生学习的积极性，也可以让学生们感受到数学家的人格魅力，鼓励学生努力学习。

四、课程与专业结合，实现学以致用

复变函数与积分变换不同于数学专业的复变函数论，复变函数是理论基础，而其重点则是积分变换，积分变换对工科学生的后续课程有着重要的作用。很多数学专业出身的老师，对相关的背景知识不甚了解，仅仅将概念和方法灌输给学生，而不讲在实际问题中到底有何作用，学生感觉很枯燥，也缺乏学习的动力。

我们在教学中注重理论联系实际，结合应用背景来讲解概念和理论，让学生了解这门学科的意义，增强了学习的积极性。例如，在讲解积分变换时向学生介绍傅氏变换的本质是时域与频率域之间的转化，因此广泛应用于信号分析，比如信号处理中的信号消噪过程；而拉氏变换的本质时域与复频域间的转化，由于其微分性质，广泛应用于微积分方程的求解，是自动控制课程中非常常用的工具。同时，利用多媒体手段，将傅里叶变换和拉普拉斯变换在电路分析、通信工程、信号处理等专业课程中的应用刻画出来，很好地解决了理论与实际相脱节的问题，帮助学生建立明确的学习目标，增强学好这门课程的信心。◇