基于改进NSGA-Ⅱ的航空发动机管路多目标布局优化
柳 强,焦国帅
(辽宁石油化工大学 信息与控制工程学院,辽宁 抚顺 113001)
0 引言
管路作为电、油、水、气等的载体,在工厂、航空、汽车、船舶等领域广泛应用,其设计质量对产品或整个系统的性能具有重要的影响。针对航空发动机出现的空中停车事故,美国通用电气公司经过一系列调查后[1],发现引起空中停车事件的真正原因有一半由管路问题引起。例如,一台典型的航空发动机通常包括数百根管路及线缆,这些管路的排布质量和效率对发动机的设计周期、成本及效率有重要影响。由于三维空间内的管路敷设问题已属于非确定多项式(Non-Deterministic Polynomial, NP)难问题,同时还需考虑多种目标及约束,因此其管路设计问题已成为复杂产品开发的关键环节。
为提高管路系统的设计质量和效率,多年来国内外学者提出了多种自动敷设算法。Rourke[2]将迷宫算法应用于管路布局问题,详细描述了管路布局的几何结构,该算法虽然绕障能力强且能保证最短路径,但所需的容量大,操作速度慢;柳强等[3]和吴宏超等[4]分别提出基于工程规则的三维启发式布管算法和基于改进A*算法的管路自动布局优化方法,这种启发式搜索算法的优点是搜索速度快,存储空间小,缺点是不能保证最优路径;Liu等应用可视图法[5]建立曲面可视图来求解航空发动机机匣曲面的最短管路[6],并将可视图法推广到曼哈顿空间,提出“曼哈顿可视图”[7],这种基于图论的方法只要建立适当的图就可以保证找到最短路径,但其难以考虑其他目标和约束;刘检华等[8]提出一种管路数字化布局设计、制造与检测集成方法,建立了该方法的业务流程和应用技术框架,具有较强的智能性和综合性,并通过在某卫星制造厂中的应用验证了该方法的有效性。
智能优化算法(如遗传算法、蚁群算法、混沌算法、萤火虫算法等)作为一种新兴的优化计算技术,近年来受到了越来越广泛的重视。例如,Ito[9]提出基于遗传算法的管路规划方法,该方法首先对目标空间进行栅格建模,然后对管路长度、弯头数和能量值函数3个目标函数进行加权,将其转化为单目标优化问题,但该方法的编码方式和遗传算子不太理想;付宜利等[10]和吴宏超等[11]分别应用混沌算法和萤火虫算法对复杂机电产品的管路布局问题进行了研究;崔淑慧[12]提出一种基于改进人工鱼群算法的三维管路敷设方法,并基于UG NX开发了相应的管路敷设系统;Qu等[13]提出一种基于并行蚁群算法和三维连接图的分支管路布局方法来提高三维空间约束下的搜索效率,并用航空发动机的管路布局进行了验证。另外,管路布局问题本质上属于多目标优化问题,但现有的管路布局方法大多是将管路长度作为优化目标,或将多目标问题采用线性加权的方式转化为单目标优化问题,并未在本质上解决管路布局问题的多目标优化属性。近年来,已有一些学者开始对管路多目标布局优化问题展开研究,例如,郭秀[14]以长度、弯头数和安装性为优化目标,应用非支配遗传算法(Non-dominated Sorting Genetic Algorithm, NSGA)对直角管路多目标布局问题进行了探索;Ahmed等[15]应用第二代非支配遗传算法(NSGA-Ⅱ)对二维空间内的多目标路径规划问题进行了研究。但总体来说,由于问题的复杂性,目前管路多目标布局优化方面的研究还比较少。
本文从多目标优化角度出发,提出一种基于改进NSGA-Ⅱ的发动机管路布局方法。一方面,为了提高NSGA-Ⅱ的全局搜索能力,在现有NSGA-Ⅱ的基础上提出一种新的种群更新机制,在进化时运用拉丁超立方对部分较差个体进行替换,以达到全局搜索能力与收敛性的均衡;另一方面,对敷设空间采用凸包进行建模,基于B样条曲线设计了个体编码方式,应用改进NSGA-Ⅱ对发动机管路布局优化的Pareto解集(非支配解集)进行求解,最后通过数值算例、三维空间管路敷设、发动机机匣曲面管路敷设验证了所提方法的可行性。
1 数学模型
管路布局优化涉及多个优化目标,属于典型的多目标优化问题,其目的是在一定约束空间内寻找满足约束条件的Pareto解集。给定s个决策变量,r个目标函数,多目标优化问题的一般形式[16]描述如下:
miny=f(x)=(f(x1),f(x2),…,f(xr))。
s.t.
gi(x)≤0,i=1,2,…,q;
hj(x)=0,j=1,2,…,p。
(1)
式中:x=(x1,…,xs)∈X⊂Rs为s维的决策矢量,X为s维的决策空间;y=(y1,…,yr)∈Y⊂Rr为r维的目标矢量,Y为r维的目标空间。gi(x)≤0定义了q个不等式约束;hj(x)=0定义了p个等式约束。
1.1 优化目标
本文主要考虑管路欧氏长度f1和平滑度(弯曲角度)f2两个优化目标:
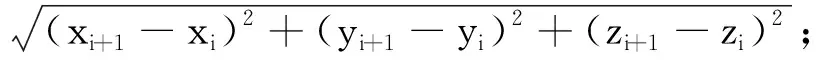
(2)
(ai×bi/(|ai|×|bi|))。
(3)
式中:(xi,yi,zi)为路径中第i个节点的坐标,m为路径中节点的数量;ai=(xi+1-xi,yi+1-yi,zi+1-zi),bi=(xi+2-xi+1,yi+2-yi+1,zi+2-zi+1),1≤i≤m。
需要说明的是,本文所使用的NSGA-Ⅱ和改进NSGA-Ⅱ都是求解极小值问题的算法,而式(3)所求得的βi是路径间夹角θi的补角(如图1),从而将极大值问题转化为求解极小值的问题。


1.2 约束条件
在管路布局过程中,应考虑多种工程约束。本文重点考虑以下约束:
(1)管路不能与障碍物(附件、电气区域、维修区域及已敷设的管路)发生干涉,即路径必须是可行的。该约束可以通过3.2.2节介绍的惩罚函数法解决,判断路径与障碍物是否发生干涉的方法将在3.2.1节详细介绍。
(2)管路弯曲角度应不小于90°,从而满足可加工性约束。该约束亦可通过3.2.2节介绍的惩罚函数法解决。
(3)管路与结构件表面之间以及不同管路之间均需预留一定间隙,以满足管路的可装配性约束。该约束可通过对障碍物模型进行“膨胀”来处理,详细处理方法见1.3节。
(4)管路应尽量靠近发动机内机匣敷设,以便获得较好的振动特性和较小的外廓尺寸。本文将管路中心线的离散点控制在机匣表面上,令其沿测地线分布,从而使管路贴近机匣表面敷设,其中机匣表面测地线方程可参考文献[6]。
(5)管路应尽可能少地从附件顶部跨过,以利于附件的设计和附件维修单元的装拆维护。该约束亦可通过约束(4)中的方法解决,令管路贴近机匣表面敷设,即排除了在附件顶部跨过的可能。
1.3 空间建模
本文采用三维凸包对敷设空间的障碍进行建模。相对现有多数方法将障碍物简化为圆柱体或长方体等规则的几何体,凸包能够更好地刻画工程应用中存在的不规则障碍物,从而提高管路布局的计算精度。例如,在三维空间中任意拾取15个点,应用MATLAB中的convhlln函数求取凸包顶点,所形成的三维凸包如图2所示。
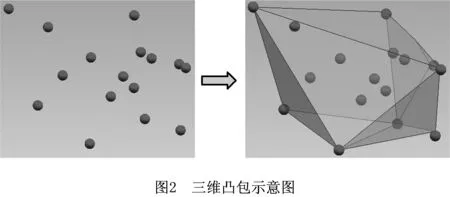
对于航空发动机机匣表面布管问题(如图3a),机匣表面为回转面,可通过UG/GRIP二次开发语言提取机匣表面某母线上采样点的坐标信息,如图3b所示。所提取的采样点坐标分别为(63.0,0,0),(63.6,0,10),(64,0,20),(64.2,0,30),(64.0,0,40),(63.2,0,50),(62.0,0,60),(60.7,0,70),(59.0,0,80),(56.5,0,90),(54.0,0,100),(52.2,0,110),(51.0,0,120),(50.1,0,130),(50.0,0,140),(51.2,0,150),(53.0,0,160),(54.7,0,170),(56.0,0,180),(56.5,0,190),(56.0,0,200),(54.2,0,210),(52.0,0,220),(50.0,0,230),然后将其转化为柱坐标,并应用最小二乘法进行拟合,即可得到内机匣母线柱坐标方程。机匣母线柱坐标方程和测地线方程详见文献[3,6],附件可应用测地线代替直线建立“曲面凸包”[6]进行建模,如图3c所示。
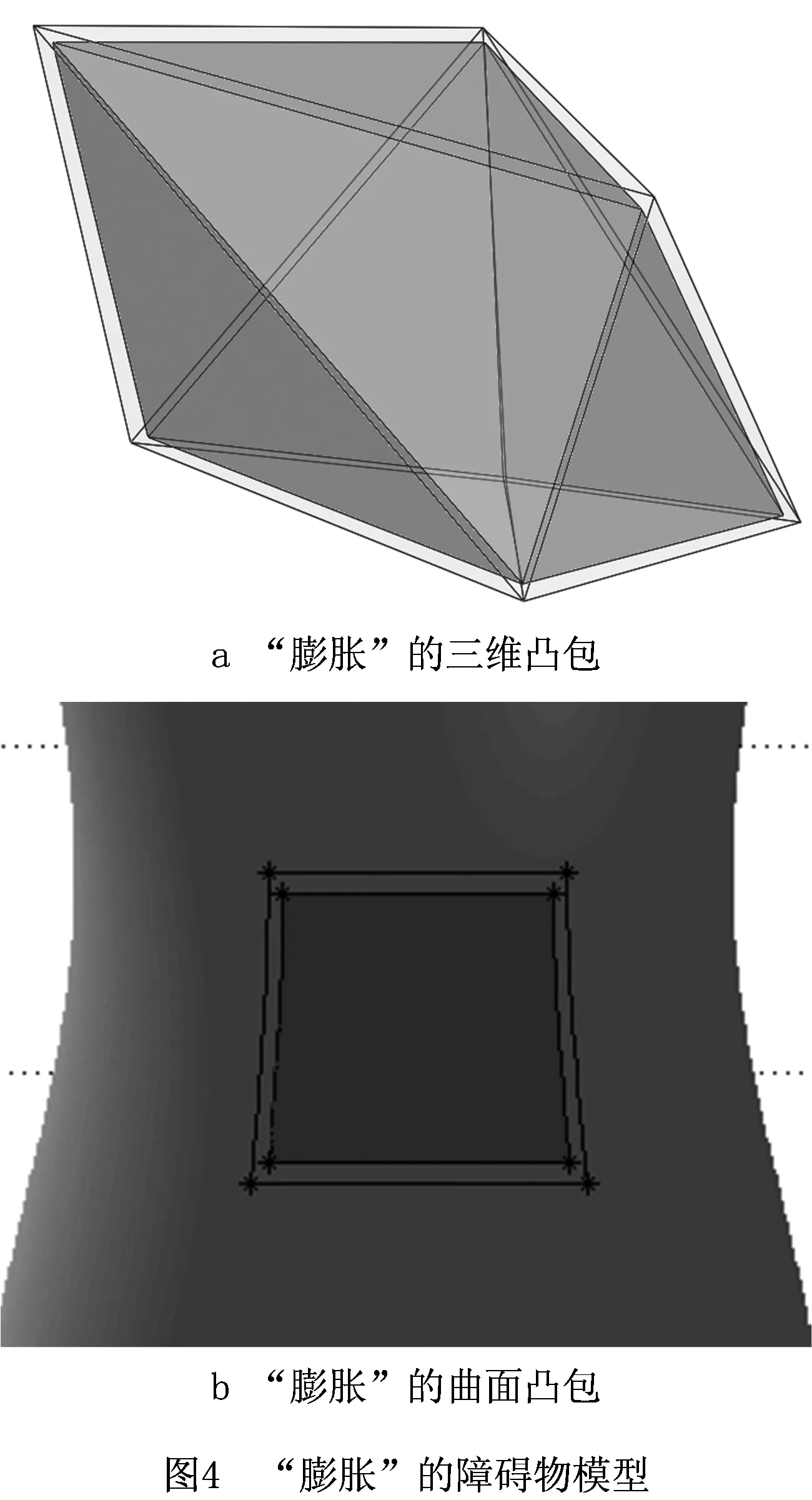
此外,为了满足管路的可装配性约束,需要对障碍物模型进行“膨胀”处理。对于三维空间中的凸包,需要将凸包中的每个顶点向外适当延伸,结果如图4a所示;对于航空发动机机匣表面的“曲面凸包”,需要将“曲面凸包”中靠近机匣表面的4个顶点进行延伸,结果如图4b所示。
2 改进的NSGA-Ⅱ算法
2.1 基本NSGA-Ⅱ算法
NSGA-Ⅱ是Deb等[17]于2002年对其算法NSGA的改进算法,它是迄今为止多目标优化领域应用最广泛的算法之一。相对于NSGA而言,NSGA-Ⅱ的主要特点如下:
(1)使用一种新的基于分级的快速非支配解排序方法,降低了计算的复杂度,使算法的复杂度由原来的O(rN3)降到O(rN2),其中r表示目标函数的数目,N表示种群中个体的数目。
(2)应用拥挤度的概念,克服了NSGA中需要人为指定共享参数的缺陷,而且使个体能够扩展到整个Pareto前沿面并尽可能均匀分布。
(3)采用精英保留机制,扩大了采样空间,使父代个体与经过交叉变异之后形成的子代个体共同竞争来产生下一代个体,以保证某些优良个体在进化过程中不会丢失,有效提高了种群的整体进化水平。
2.2 改进的NSGA-Ⅱ
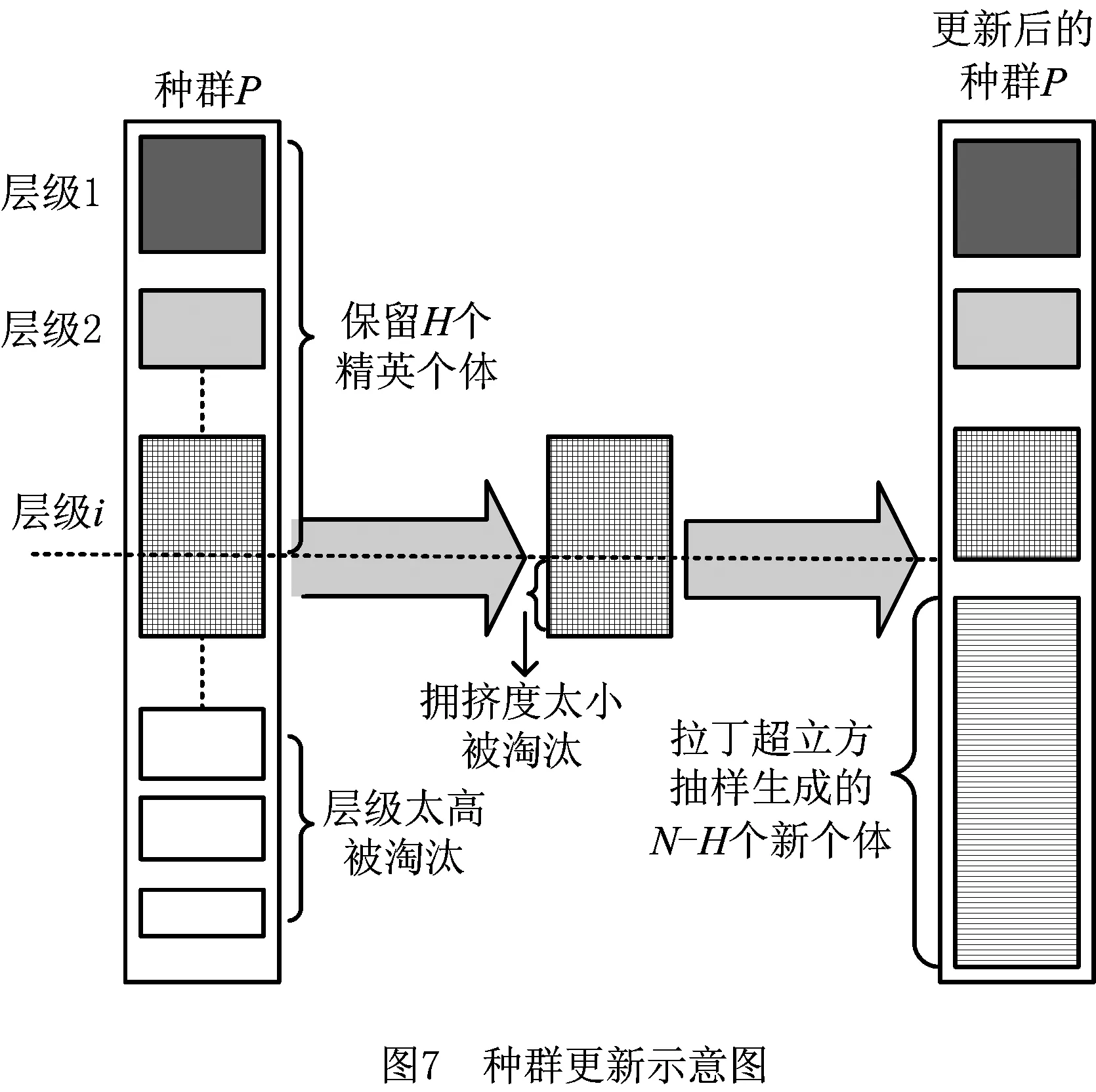
本文对NSGA-Ⅱ主要进行两方面改进。首先将拉丁超立方抽样运用于算法初始化,提高初始种群分布的均匀性。另外,提出一种新的种群更新机制,在进化过程中每隔若干代,就运用拉丁超立方抽样产生的新个体取代种群中部分质量较差的个体,同时保留原有的精英保留策略,以达到全局搜索能力与收敛性均衡。
2.2.1 基于拉丁超立方的种群初始化
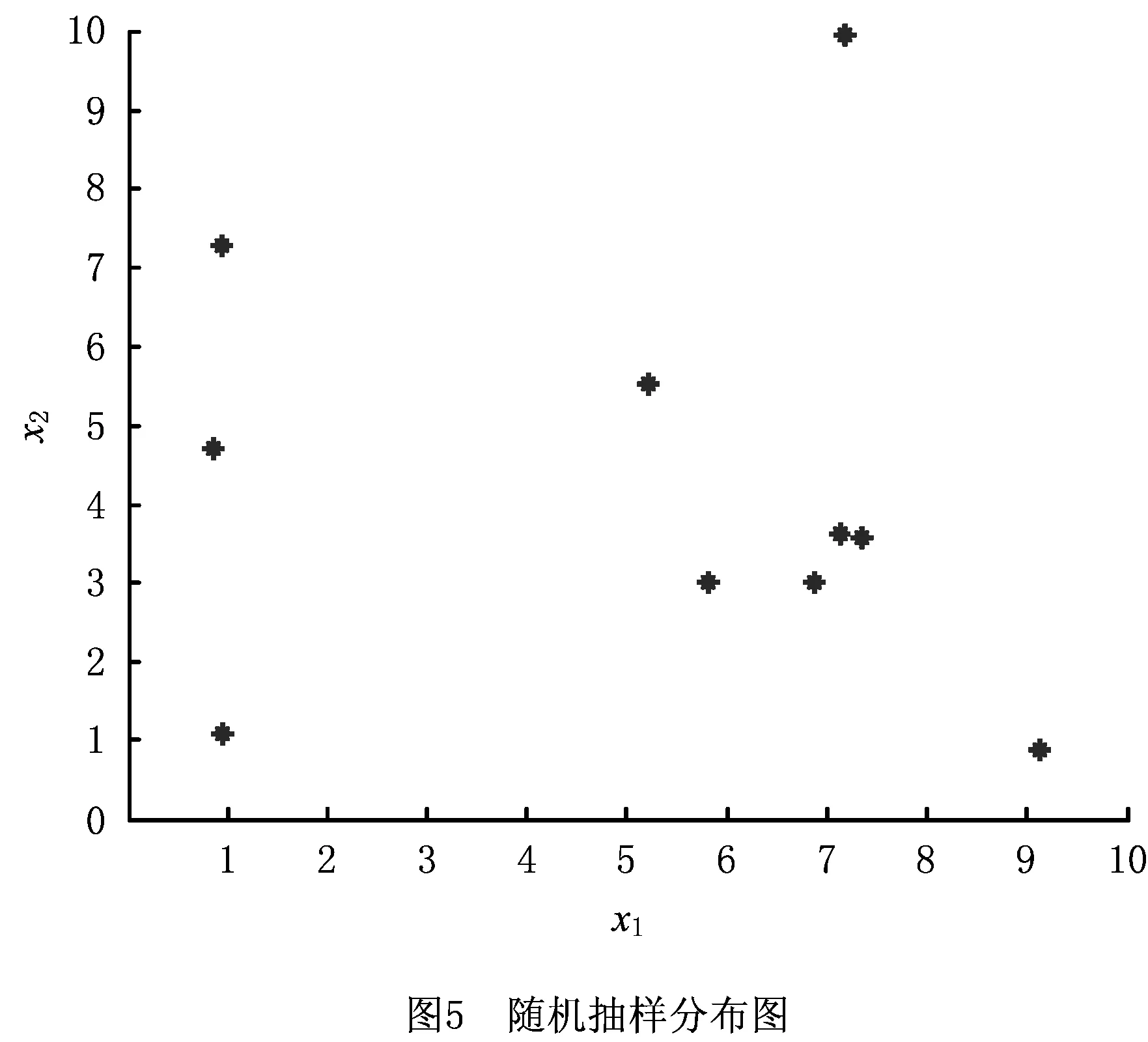
在基本NSGA-Ⅱ中,采用在限定空间内随机抽样产生样本的方法,该方法操作简单,但有时产生的样本在一些区域分布比较集中,在另外一些区域分布比较稀疏,样本的均匀性较差。假定抽样规模N=10,为方便观察,选定维数为二维,区间为[0,10],如图5所示,图中某些区域分布了较多的样本,在某些区域则较少。
拉丁超立方抽样[18]是一种多维分层抽样方法,该方法可随机地产生尽量分布均匀的样本点,同时样本数量可以设定,因此在试验设计领域应用广泛,并在改进智能优化算法方面具有较高的应用价值,例如文献[19]应用拉丁超立方方法对遗传算法(Genetic Algorithm,GA)的种群初始化和操作算子进行了改进。拉丁超立方抽样的工作原理简述如下:
(1)确定抽样规模N和维数s。
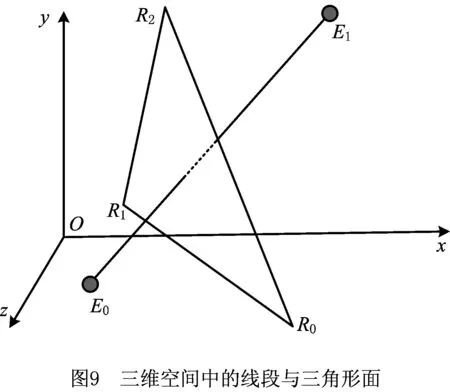
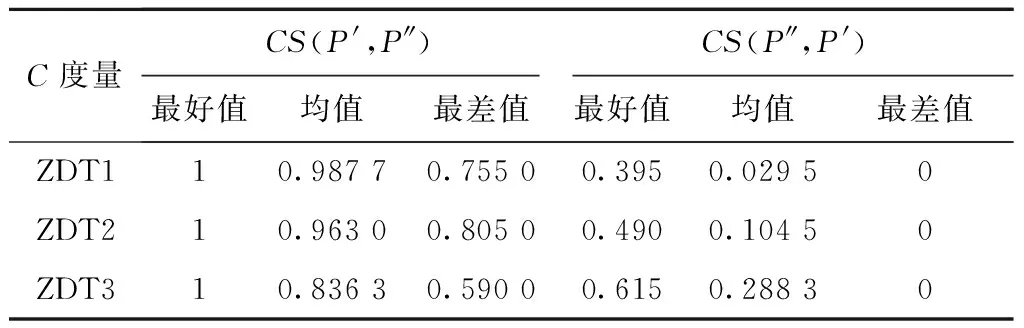
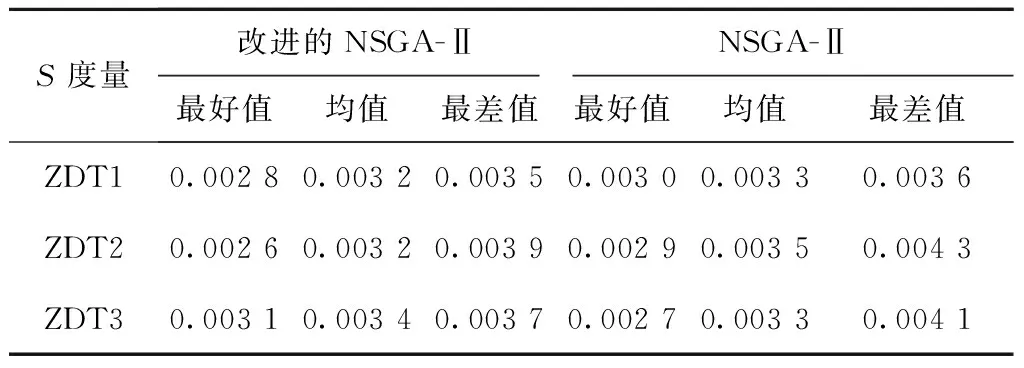
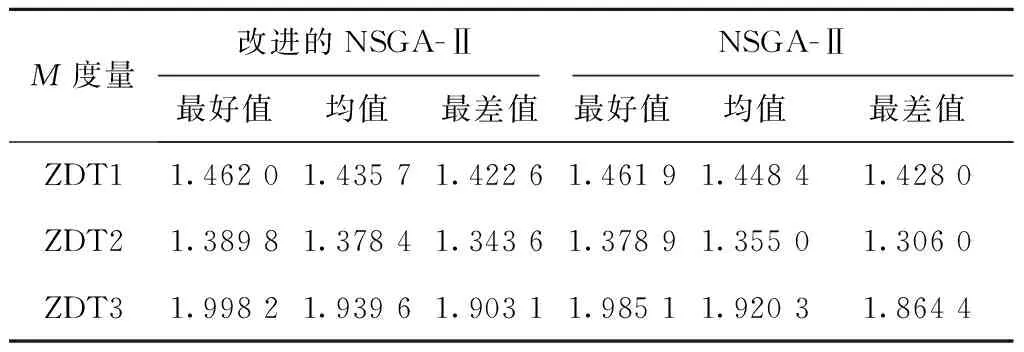
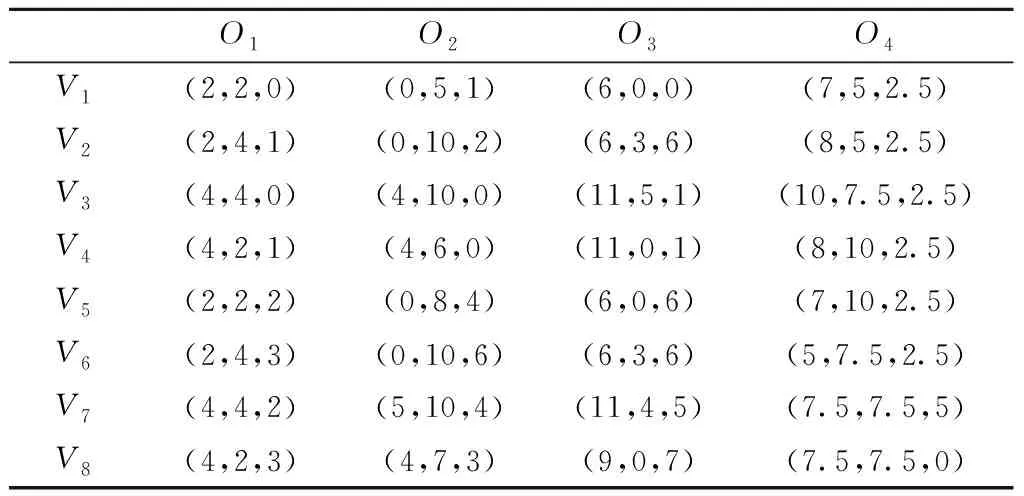
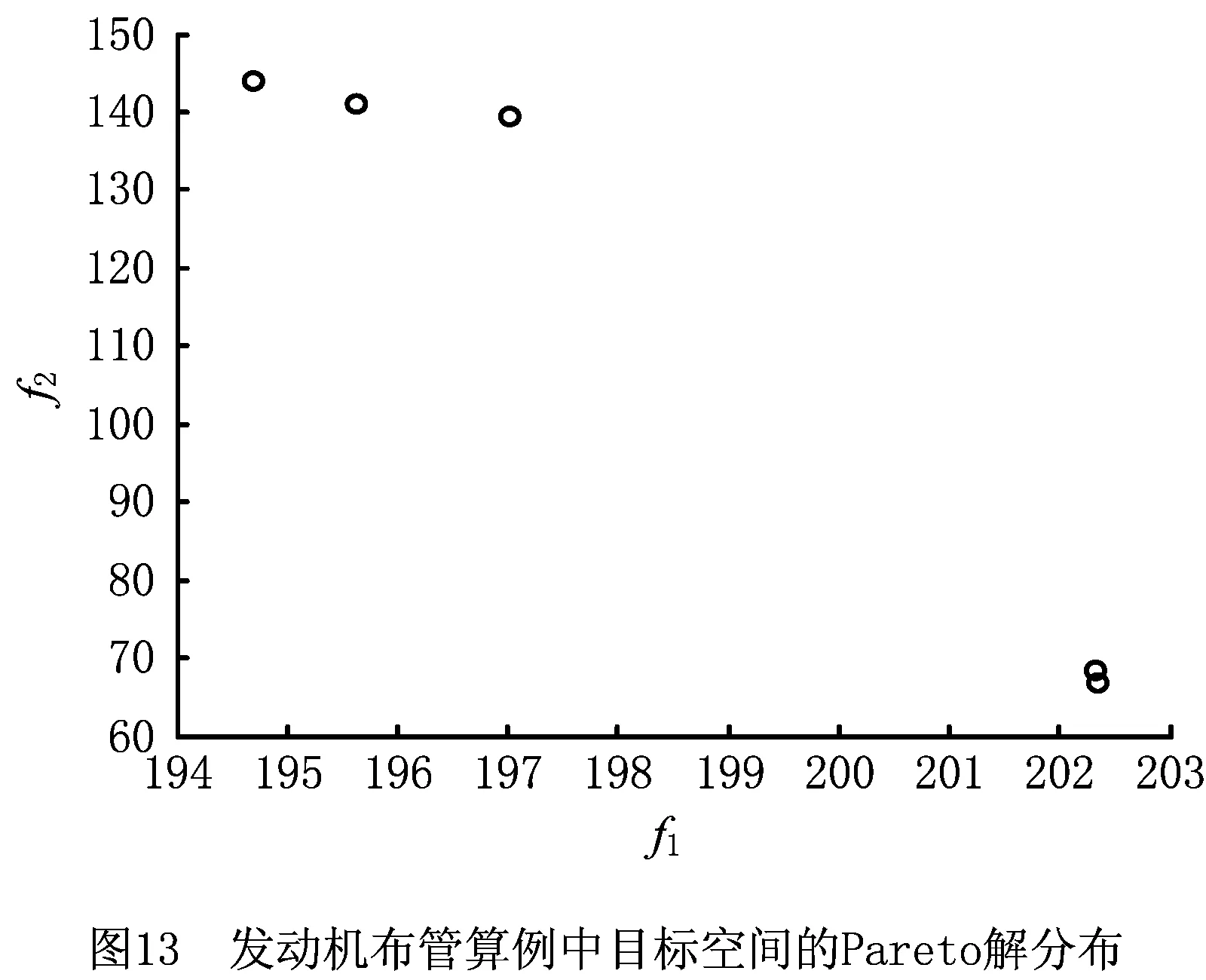
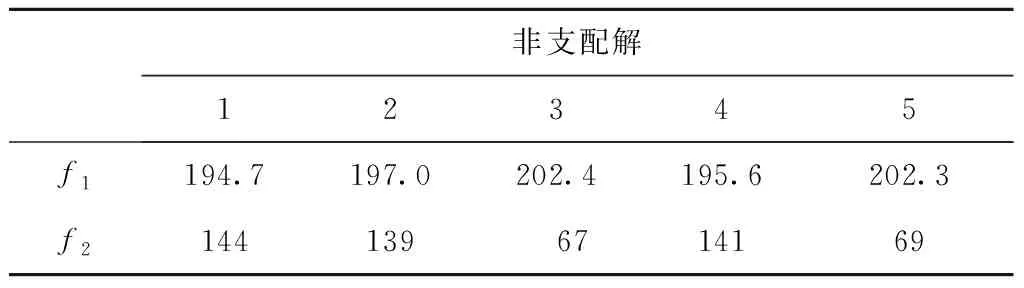
(2)将每维变量xi的定义区间[xl,xu]划分成N个相等的小区间,即xl=xi0 (3)生成一个N×s矩阵,矩阵的每列都是数列{1,2,3,…,N}的一个随机全排列。 (4)矩阵的每行对应一个被选中的小超立方体,在每个被选中的小超立方体内随机产生一个样本,从而选出N个样本。 应用拉丁超立方抽样产生的样本如图6所示。通过对比图5和图6可知,拉丁超立方抽样产生的样本在在满足随机性的同时具有更好的均匀性。因此,本文采用拉丁超立方的方式对NSGA-Ⅱ种群进行初始化,使初始种群随机且分布均匀,为下一步种群迭代进化提供较好的初始解。 2.2.2 基于拉丁超立方与差解淘汰的种群更新机制 基本NSGA-Ⅱ具有较好的收敛性和鲁棒性,能够在一定的进化代数内得到非支配解集,但有时会过早收敛而陷入局部最优。为了进一步提高NAGA-Ⅱ的全局性,本文提出一种新的种群更新机制,即在传统精英保留策略的基础上,应用拉丁超立方方法对差解进行淘汰替换的种群更新策略。该更新机制描述如下: 设种群数目为N,迭代次数为G,定义变量Q表示种群更新的间隔代数(Q 改进NSGA-Ⅱ的具体步骤如下: 步骤1开始,设置初始参数。 步骤2运用拉丁超立方抽样产生数量为N的初始种群PT,并对种群PT进行快速非支配排序。 步骤3对快速非支配后的种群PT进行选择、交叉、变异操作,产生数量为N的子代种群D。 步骤4合并种群PT,D,对合并的种群进行快速非支配排序,并采用精英保留策略从2N中选出N个个体作为新的种群PT。 步骤5先判断此时的进化代数是否等于最大迭代次数,若相等,则算法停止,输出结果;否则,再判断此时的进化代数能否被种群更新的间隔代数Q整除,是则执行步骤6,否则转步骤3。 步骤6对种群PT进行基于拉丁超立方与差解淘汰的更新操作,然后转步骤3。 管路路径可以由一系列路径节点确定并控制,因此这些节点坐标可以作为个体编码,文献[10,14]均采用了该编码方式。本文将管路路径的节点序列作为个体编码,同时考虑管路的平滑性,基于节点序列建立B样条曲线对管路路径进行表达,具体为 P={(x1,y1,z1),(x2,y2,z2),…,(xm,ym,zm)。 (4) 式中m表示路径中的节点数目。一条完整的路径还需加入起始点坐标(x0,y0,z0)和终止点坐标(xt,yt,zt)。 进一步为了提高精度,在每两个节点之间均匀生成若干离散点,利用B样条曲线对这些离散点进行曲线拟合,图8所示为UG平台下的B样条曲线示意图。为了方便计算,在求目标函数f1时仍然用式(2)做近似计算。 3.2.1 判断路径与障碍物是否发生干涉 在管路布局问题中,由于存在障碍物,有相当一部分个体可能会与障碍物发生干涉,这种与障碍物发生干涉的个体称为不可行解或非法解。三维凸包的每个面都由多边形构成,每个多边形面均可分解为若干三角形面,本文将判断路径是否与三维凸包发生干涉的问题转化为判断三维空间中任意一条线段与三角形面是否相交的问题。 如图9所示,E0,E1为路径中的两个节点,R0,R1,R2为构成三维凸包的多边形面中任意一个三角形面的顶点。线段E0E1上的点可用E0+(E1-E0)×t表示,三角形面上的点可表示为R0+(R1-R0)×u+(R2-R0)×v,其中0≤t≤1,0≤u≤1,0≤v≤1。 首先使式(5)成立,然后对式(5)进行化简和等价变换得到式(6),并对t,u,v求解得式(7)。通过t,u,v的值,判断线段是否与三角形面相交。若u+v≤1&0≤t≤1&u≥0&v≥0,则线段与三角形面相交;若(u=1&v=0&0≤t≤1)|(v=1&u=0&0≤t≤1),则线段与三角形面的交点在棱边上;若都不满足,则线段与三角形面不相交。 E0+(E1-E0)t=R0+(R1-R0)u+ (R2-R0)v; (5) (6) (7) 通过上述方法可以判断三维空间中的一条线段是否与三角形面相交,以及线段是否与包含这个三角形面的多边形面相交,以及线段是否与三维凸包相交,从而可以判断整个路径是否与约束空间内的所有障碍物相交。对于发动机机匣曲面布管问题,该问题可转化为测地线段与曲面凸包的线段求交问题。 3.2.2 对与障碍物发生干涉路径的处理机制 对于与障碍物发生干涉的个体,本文采用两种处理机制。首先,在算法每次进化过程中,在子代种群与父代种群合并前直接剔除父代种群中与障碍物相交的个体;其次,将合并后种群中与障碍物发生干涉的个体运用惩罚函数进行处理,即 (8) 式中:fi为第i个目标函数的值,i=1,2;α为惩罚系数,当个体与障碍物发生干涉时α=100,否则α=1。上述惩罚函数法也适用于对约束条件(2)的处理,即用式(8)对弯曲角度小于90°的个体进行惩罚。 管路敷设算例通过MATLAB与UG联合实现,其中UG实现三维建模及敷设结果可视化,MATLAB实现敷设算法,二者通过txt文本进行数据传输。对于发动机机匣曲面布管情况,可用测地线代替直线在机匣表面实现所提布管方法。所提布管算法的总体流程如图10所示。 为了验证所提算法的可行性,对所提算法进行算例测试,测试分为数值算例测试和管路敷设算例测试。测试计算机硬件环境:CPU为3.20 GHz Intel(R)core(TM)i5-4460,内存4 G,编程环境为MATLAB R2010a。 本文将ZDT问题中的ZDT1,ZDT2,ZDT3作为测试函数。ZDT问题[20]自2000年由Zitzler等提出以来,被广泛的应用于多目标优化的测试领域,具体形式如下: (9) 式中:n=30;0≤xi≤1,i=1,2,…,30。 本文采用C-度量[21](两个解集之间的覆盖率)、S-度量[22](spacing metric)和M-度量[23](maximun spread-measure)分别评估解的收敛性、解分布的均匀性和解的宽广性,具体定义如下: (1)C-度量 计算两个解集之间的相对覆盖率,令P′,P″为目标空间中的两个非支配解集,将(P′,P″)映射到[0,1]之间得到P′和P″之间的覆盖率CS: (12) 若P′中所有点都支配或等于P″中的所有点,则CS(P′,P″)=1,反之CS(P″,P′)=0。必须同时考虑CS(P′,P″)和CS(P″,P′),若CS(P′,P″) (2)S-度量 计算解集的分布度 (13) (3)M-度量 计算解集P′中所有解构成的多面体的周长 (14) 式中:n为非支配解的个数,m为目标空间的维数。解集P′的范围越宽广,相应的M值越小。 改进NSGA-Ⅱ和基本NSGA-Ⅱ涉及的共同参数设置如下:种群大小N=200,迭代次数T=300,交叉概率Pc=0.9,变异概率Pm=0.1,改进NSGA-Ⅱ 中种群更新的间隔代数Q=50,种群更新时保留的精英个体H=100。对每个函数独立运行20次,记录每次运行得到的数据,表1~表3分别是改进NSGA-Ⅱ和基本NSGA-Ⅱ对上述测试函数的C-度量、S-度量、M-度量的比较。 表1 改进NSGA-Ⅱ和NSGA-Ⅱ的C-度量 注:P′,P″分别表示改进NSGA-Ⅱ和NSGA-Ⅱ得到的Pareto解集。 表2 改进NSGA-Ⅱ和NSGA-Ⅱ的S-度量 表3 改进NSGA-Ⅱ和NSGA-Ⅱ的M-度量 从表1可见,对于ZDT1,ZDT2,ZDT3,改进NSGA-Ⅱ无论最好值、均值还是最差值均优于NSGA-Ⅱ,说明改进NSGA-Ⅱ的收敛性优于原始的NSGA-Ⅱ,从而验证了改进NSGA-Ⅱ的收敛性。从表2可见,改进NSGA-Ⅱ除了在ZDT3的最好值和均值上比NSGA-Ⅱ稍差一些外,其他数据均优于NSGA-Ⅱ。从表3可见,改进NSGA-Ⅱ除了在ZDT1的均值和最差值上比NSGA-Ⅱ稍差一些外,其他数据均优于NSGA-Ⅱ。 由表1~表3可知,改进NSGA-Ⅱ的预期目标已经基本达到,即通过拉丁超立方产生初始种群增加初始解分布的均匀性,并通过种群更新机制增加解分布的多样性,达到了收敛性与全局搜索能力的均衡。 改进NSGA-Ⅱ的参数设置如下:种群大小N=100,迭代次数T=60,交叉概率Pc=0.9,变异概率Pm=0.1,种群更新的间隔代数Q=20,种群更新时保留的精英个体H=50。 4.2.1 三维空间管路敷设算例 在三维空间管路敷设模型中,涉及的4个障碍均采用三维凸包建模,“膨胀”之后的凸包几何信息如表4所示。起始点坐标为(0.5,0.5,0.5),终止点的坐标为(10,10,2.5),得到的Pareto解集如图11所示,对应的个体信息如表5所示,对应的管路布局结果如图12所示。结果表明,在一般三维布管空间中得到的一组Pareto解集不但满足约束条件,而且分布较为均匀,验证了所提方法的有效性。 表4 三维凸包的几何信息 注:O1,O2,O3,O4分别表示布管空间中的三维凸包,V1,V2,V3,V4,V5,V6,V7,V8分别表示三维凸包的顶点。 表5 三维布管算例Pareto解集的个体信息 x1y1z1x2y2z2f1f241385516.2785.8624478516.0485.9363585216.3074.6532395415.9489.62 4.2.2 发动机机匣表面的管路敷设算例 本文采用如图3所示的简化的发动机机闸表面管路布局模型,其中圆柱型障碍物的底面圆心坐标为(-9.7,48.9,122.0),半径为12,其他曲面凸包几何信息如表6所示,以上提到的均为“膨胀”之后的几何信息。得到管路布局的Pareto解集如图13所示,对应的Pareto解集信息如表7所示,对应的管路布局结果如图14所示(模型中的直角管路表示已经敷设的管路,相当于障碍物)。结果表明,在发动机曲面布管中能够得到一组满足约束条件的Pareto解集,管路的平滑性也较好,减小了管内流阻,设计者可以根据需要选取敷设方案。 表6 曲面凸包的几何信息 注:O1,O2,O3,O4,O5分别表示发动机曲面布管空间中的曲面凸包,V1,V2,V3,V4分别表示曲面凸包中靠近机匣表面的顶点。 表7 发动机布管算例Pareto解集信息 非支配解12345f1194.7197.0202.4195.6202.3f2144139 6714169 本文提出一种改进NSGA-Ⅱ,在原有的精英保留策略基础上,提出基于拉丁超立方方法的差解淘汰替换策略,以实现算法收敛性与全局搜索能力的均衡。同时,以管路长度及平滑性为优化目标,应用改进NSGA-Ⅱ求解了发动机管路布局优化的Pareto解集。与传统的布管方法相比,本文所提方法可以得到一组非支配解集,设计人员可以根据工程经验选择适当的布局方案。另外,所提方法既适用于发动机曲面布管,又适用于一般三维空间,具有很好的通用性。后续研究可在管路多目标布局优化过程中进一步考虑管路系统的振动指标等。 参考文献: [1] FAN Jiang. Research on MAS based distributed cooperative aero-engine outside pipe system design[D]. Beijing:Beihang University,2003(in Chinese).[樊 江.航空发动机外部管路多代理协同设计系统研究[D].北京:北京航空航天大学,2003.] [2] ROURKE P W. Development of a three-dimensional pipe routing algorithm[D]. Bethlehem,Germany:Lehigh University,1975. [3] LIU Qiang, WANG Cheng’en, BAI Xiaolan. Engineering rules-based pipe routing algorithm for aero-engines[J]. Chinese Journal of Mechanical Engineering,2011,47(5):163-169(in Chinese).[柳 强,王成恩,白晓兰.基于工程规则的航空发动机管路敷设算法[J].机械工程学报,2011,47(5):163-169.] [4] WU Hongchao, LIU Jianhua, TANG Chengtong, et al. Automatic pipe layout design and optimization method based on improved A*algorithm[J].Computer Integrated Manufacturing Systems,2016,22(4):945-954(in Chinese).[吴宏超,刘检华,唐承统,等.基于改进A*算法的管路自动布局设计与优化方法[J].计算机集成制造系统,2016,22(4):945-954.] [5] LIU Qiang, WANG Cheng’en. A graph-based pipe routing algorithm in aero-engine rotational space[J]. Journal of Intelligent Manufacturing,2015,26(6):1077-1083. [6] LOZANO-PÉREZ T, WESLEY M A. An algorithm for planning collision-free paths among polyhedral obstacles[J]. Communications of the ACM,1979,22(10):560-570. [7] LIU Qiang. A rectilinear pipe routing algorithm:manhattan visibility graph[J]. International Journal of Computer Integrated Manufacturing,2016,29(2):202-211. [8] LIU Jianhua, LIU Shaoli, NING Ruxin, et al. Integrated technology digital pipeline routing, manufacturing and inspection[J]. Computer Integrated Manufacturing Systems,2015,21(4):941-945(in Chinese).[刘检华,刘少丽,宁汝新,等.管路数字化布局设计与制造及检测集成技术[J].计算机集成制造系统,2015,21(4):941-945.] [9] ITO T. A genetic algorithm approach to pipe route path planning[J]. Journal of Intelligent Manufacturing,1999,10(1):103-114. [10] FU Yili, FENG Haibo, SUN Jianxun, et al. Auto-routing of electromechanical products based on chaos algorithm[J]. Computer Integrated Manufacturing Systems,2007,13(3):497-502(in Chinese).[付宜利,封海波,孙建勋,等.基于混沌算法的机电产品管线自动敷设研究[J].计算机集成制造系统,2007,13(3):497-502.] [11] WU Hongchao, LIU Jianhua, TANG Chengtong, et al. Optimization technology of pipeline system layout sequence based on firefly algorithm[J].Computer Integrated Manufacturing Systems,2016,22(8):1837-1848(in Chinese).[吴宏超,刘检华,唐承统,等.基于萤火虫算法的管路系统布局序列优化技术[J].计算机集成制造系统,2016,22(8):1837-1848.] [12] CUI Shuhui.Research on three dimensional pipe auto routing algorithm and interference check method[D]. Harbin:Harbin Institute of Technology,2015(in Chinese).[崔淑慧.三维管路自动敷设算法及干涉校验方法研究[D].哈尔滨:哈尔滨工业大学,2015.] [13] QU Yanfeng, JIANG Dan, YANG Qingyan. Branch pipe routing based on 3D connection graph and concurrent ant colony optimization algorithm[J]. Journal of Intelligent Manufacturing,2016:1-11.DOI: 10.1007/s10845-016-1203-4. [14] GUO Xiu. Research on pipe multi-objective routing based on GA[D]. Fushun:Liaoning Shihua University,2015(in Chinese).[郭 秀.基于GA的管路多目标布局优化方法研究[D].抚顺;辽宁石油化工大学,2015.] [15] AHMED F, DEB K. Multi-objective optimal path planning using elitist non-dominated sorting genetic algorithms[J]. Soft Computing,2013,17(7):1283-1299. [16] WENG Liguo, JI Zhuangzhuang, XIA Min, et al.Robot path planning based on improved multi-objective particle swarm[J]. Chinese Journal of Mechanical Engineering,2014,26(12):2892-2898(in Chinese).[翁理国,纪壮壮,夏 旻,等.基于改进多目标粒子群算法的机器人路径规划[J].系统仿真学报,2014,26(12):2892-2898.] [17] DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multi-objective genetic algorithm:NSGA-Ⅱ[J]. IEEE Transaction on Evolutionary Computation,2002,6(2):182-197. [18] MACKAY B M D, BECKMAN R J, CONOVER W J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code[J]. Technometrics,2010,42(1):55-61. [19] ZHOU Benda, YAO Hongliang, CHEN Minghua. Improved genetic algorithm based on Latin hypercube sampling and immune mechanism[J].Journal of Computer Applications,2011,31(4):1103-1106(in Chinese).[周本达,姚宏亮,陈明华.基于拉丁超立方体抽样和免疫机制的改进遗传算法[J].计算机应用,2011,31(4):1103-1106.] [20] ZITZLER E, DEB K, THIELE L. Comparison of multi-objective evolutionary algorithms:empirical results[J]. evolutionary Computation,2000,8(2):173-195. [21] ZHENG Jinhua. Multiple objective evolutionary algorithms and its applications[M]. Beijing:Science Press,2007(in Chinese).[郑金华.多目标进化华算法及其应用[M].北京:科学出版社,2007.] [22] SCHOTT J R. Fault tolerant design using single and multicriteria genetic algorithm optimization[J]. Cellular Immunology,1995,37(1):1-13. [23] DEB K, KALYANMOY D. Multi-objective optimization using evolutionary algorithms[M]. New York,N.Y.,USA: John Wiley & Sons, Inc,2001.
2.3 改进NSGA-Ⅱ的执行步骤
3 基于改进NSGA-Ⅱ的管路多目标布局优化
3.1 编码方式

3.2 避障机制
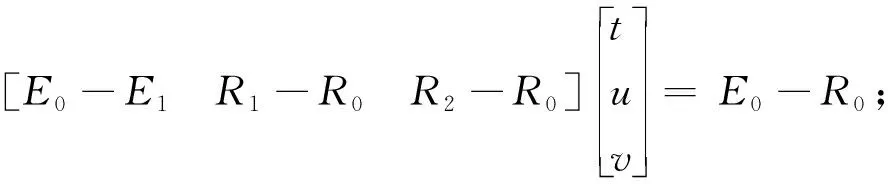
3.3 算法流程

4 仿真实例与分析
4.1 数值算例
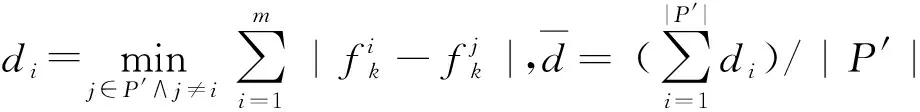
4.2 管路敷设算例



5 结束语


