列车转向架关键部件预防性维修决策优化模型
贺德强,罗 安,邓建新,谭文举
(1.广西大学 机械工程学院,广西 南宁 530004;2.广西制造系统与先进制造技术重点实验室,广西 南宁 530004;3.南宁轨道交通集团有限公司,广西 南宁 530029)
0 引言
目前,我国城市轨道交通列车转向架关键部件的维修主要采用基于状态修和事后修的计划预防维修模式[1-2]。预防性维修是按规定的时间间隔对列车转向架关键部件进行维修,能够在一定程度上防止或者延迟故障,但有可能出现欠维修或者过维修的问题。状态预防修能够在一定程度上避免故障的发生,但其按照规定的时间间隔周期进行维修将会使列车在运营阶段频繁停运检修,降低了运营效率[3]。事后预防维修是故障发生后进行的一种被动维修模式,虽然可以避免过维修现象,但是如果列车在运营过程中,某些关键部件出现故障,则会造成难以估计的损失。
国内外研究人员对设备系统关键部件的维修模式进行了深入研究,特别是以预防维修模式为出发点,结合关键部件的可靠性,通过整合算法来优化检修模型。王灵芝等[4-5]提出以可靠性为中心的预防性维修计划,在此基础上分析了生产设备各单部件最优的预防性维修策略,提出多部件成组预防性维修经济性优化模型和多部件设备非周期预防性维修计划优化方法;金玉兰等[6]基于可靠性为中心的预防性维修计划,针对生产的重要性及其制定的复杂性提出多部件设备非周期预防性维修计划的优化方法;韩帮军等[7]建立了预防性维修周期间故障率的递推关系式,给出了有限时间区间的设备预防性维修策略的非线性优化模型,并用遗传算法进行优化;TSAI等[8]研究了设备关键部件的预防性维修策略,对每个组件的役龄均值和可靠度平均下降时间进行分析,通过优化部件可靠性,使其达到最大化,从而确定组件的替换周期;侯文瑞等[9]采用可靠度恢复因子描述具有独立可靠度分布函数的多部件系统在不同维修方式下的可靠度演化规则,建立了基于可靠度的多部件系统机会维护模型,并利用蒙特卡洛仿真方法对模型进行优化;NI等[10]将预防性维护机会运用于大型生产系统中,结合系统可靠性和生产要求确定了优化模型;LAGGOUNE等[11]提出一种随机故障的多分量系统预防计划维修模型,利用智能群搜索方法对该模型进行优化;周晓军等[12]结合役龄递减因子和故障率递增因子的优点,通过引入基于两类调整因子的混合式故障率演化规则,建立了基于设备可靠性的顺序预防性维护优化模型。
以上学者对系统关键部件的预防维修研究,基本是从部件的可靠性角度进行优化分析,针对列车关键部件检修活动中的预防性维修决策优化研究比较少见。本文综合考虑多种维修模式下的列车转向架关键部件,通过记录分析部件役龄周期和维修费用,结合最小修维修形式提出列车关键部件预防性维修决策优化模型。通过最大最小蚁群(Maximum and Minimum Ant System, MMAS)算法求解模型,以平均最小费用率为优化目标,通过仿真分析确定列车关键部件的维修策略。
1 列车关键部件机会维修建模假设与策略
1.1 建模假设
(1)列车关键部件检修周期以列车年检为准。
(2)列车关键部件以转向架5个部件(轴承、轮对、轴箱、减震装置、抗侧滚扭杆)为例。
(3)列车关键部件的故障率是独立的,遵循威布尔分布,且只考虑部件之间的维修周期与经济相关性。
(4)部件i在单个维修周期中的总维修次数为Z。
(5)除了最小维修模式,如果部件的损坏程度超过维修能力范围,则将对损坏部件进行更换。
(6)最小维修时间很短,其固定维修费用可以忽略不计。
(7)关键部件的可靠性随着役龄时间的增加而逐渐下降。
1.2 机会维修策略分析
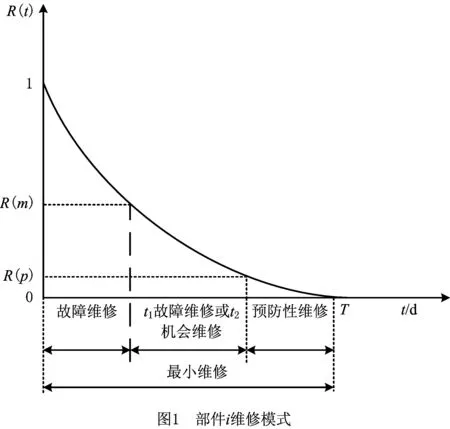
列车转向架由若干个关键部件组成,本文拟采用基于机会策略的列车关键部件预防性维修决策优化模型对转向架关键部进行维修。如图1所示,在整个运行周期(0,T)内,需要对部件i进行日常维护检修,这里采用最小维修(如除尘、润滑、清洁、检测等)的方式。当部件在(0,t1)之间发生故障时,进行故障维修。当运行时间在(t1,t2)之间时,如果部件i发生故障则进行故障维修;如果在部件i维修的同时其他部件出现故障或达到预防性维修周期,则对其他部件进行机会维修。当部件的运行时间达到t2时,进行预防性维修。
2 列车转向架关键部件的机会维修模型
2.1 列车转向架关键部件的故障维修概率
列车转向架关键部件主要由轴承、轮对、轴箱、减震装置、抗侧滚扭杆5个部件组成,疲劳强度、磨损寿命、腐蚀寿命以及多单元组成系统的寿命多服从威布尔分布。因此,这些部件的故障时间服从威布尔分布,则有
(1)
式中:h(t)为部件i的故障概率密度函数;η为特征寿命参数(单位:d);β为部件的形状参数,β>1。
2.2 列车转向架关键部件的机会维修概率
当部件经过相应周期运行磨合之后,其故障概率会趋向于一个稳定的数值。由图1关键部件维修模式可知,部件i能够通过其他部件的故障维修概率λfi或者预防性维修概率λpi两种情况进行检修[13]。
指数分布是威布尔分布的一种特殊情况,由指数分布的概率密度分布特点和可靠性的理论知识可知:
(2)
(3)
令
Pi(t,t1)=δie[-δi(t-t1)];
(4)
(5)
式中:Pi(t,t1)为机会维修概率密度函数;δi为机会维修概率;R为列车转向架关键部件的个数。
根据部件的故障概率密度函数和机会维修概率密度函数,结合图1中部件i的维修模式可知,4种维修模式的次数分别为:
(1)当t∈(0,T)时,均需要对部件i进行最小维修,则其维修次数

(6)
(2)当t∈(0,t1)时,如需对部件i进行故障维修,则其故障维修次数
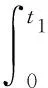
(7)
(3)当t∈(t1,t2)时,部件的维修分为以下两种情况:
1)因为本身的故障被维修,即部件i在t时刻发生故障,且在(t1,t2)期间没有其他部件出现故障或进行预防性维修使部件i产生机会,所以相应的故障维修次数

(8)
2)因为机会被维修,即部件i在(t1,t2)期间不发生故障,且至少有一个其他部件出现故障或进行预防性维修使部件i产生机会,所以相应的机会维修次数

(9)
因此,部件i的故障维修次数
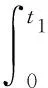
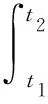
(10)
(4)当t>t2时,部件i进行预防性维修。即到t2为止,部件i既没有在任何维修周期内发生故障,也没有因为其他部件带来的机会而被维修,因此预防性维修次数
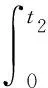
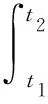
(11)
2.3 机会维修策略优化模型
假设部件i按照图1所示的4种维修模式依次进行检修,则部件i在一个维修周期内的维修费用
Ci[m]=C1i·Mi{h}+(C0+C2i)Mi{f}+
C2i·Mi{o}+(C0+C3i)·Mi{p}。
(12)
式中:C0为固定维修费用;C1i为部件i的最小维修费用;C2i为部件i的故障维修费用;C3i为部件i的预防性维修费用;Mi{h}为周期T内部件i的最小维修次数;Mi{f}为周期T内部件i的故障维修次数;Mi{o}为周期T内部件i的机会维修次数;Mi{p}为周期T内部件i的预防维修次数。
部件i的一个维修周期可以表示为
Ei[T]=t(0,t1)+t(t1,t2)+t(t2,T)+T。
(13)
由上述分析,建立如下优化模型:
(14)
s.t.
0 (15) 式中E(t1,t2)为列车转向架关键部件平均费用(单位:元/d)。 优化模型的求解往往是一个包含多个未知量、多约束、非线性的过程,上述优化模型运用MMAS算法进行迭代寻优,其求解过程如下: (2)优化模型通过人工智能优化算法能够快速有效地求解出最优解。相对比于遗传算法、粒子群算法、免疫算法等其他优化算法,MMAS算法能够通过目标的大致方向全方位、多途径地探索最优解,对初始信息素浓度进行合理分配,避免盲目搜寻,出现陷入局部最优或者停滞现象。根据搜索到的局部最优解的数值大小更新节点的信息素,能够加强局部最优解路径的信息素浓度,从而增大获得全局最优解的可能性,加快收敛速率。本文应用MMAS算法在平均费用率拓扑图上迭代寻优,分别找到优化检修周期和机会维修概率序列,该序列说明了拓扑图上节点检修周期的先后次序,按照该次序制定的检修方案,可以在满足模型E的约束条件的基础上获得使关键部件平均费用率最低的最优方案。具体步骤如下: 步骤1设置节点集合Ci和MMAS参数,将m只蚂蚁分别置于节点上开始访问,每只蚂蚁按照一定概率转移至下一个节点,然后计算各只蚂蚁的路径长度,记录为当前的最好解。 步骤2按照信息更新原则对路径信息进行更新,修改轨迹的强度,直到完成全部节点的访问。 步骤3各只蚂蚁的访问路径长度不一样,根据模型E的优化目标对各只蚂蚁访问路径的解进行评价,选择路径较短的解作为当前值来更新拓扑图状态,在后续的迭代过程中随着路径变短,信息素逐渐增强,访问该路径的蚂蚁数逐渐增多。 步骤4比较当前迭代次数与总次数,找到并输出最优解。最优序列算法流程如图3所示。 以列车转向架的轴承、轮对、轴箱、减震装置、抗侧滚扭杆5个部件为例,分别编号为1,2,3,4,5。表1所示为列车转向架关键部件的威布尔分布参数,表2所示为某地铁公司单列车所有转向架同一类关键部件的一次维修平均费用。 表1 列车转向架关键部件的威布尔参数 表2 列车转向架关键部件的维修费用 元 在实施机会预防性维修决策之前,部件主要采用最小修和故障修为主的检修模式进行检修,其维修费用包括最小修费用或故障维修费用,以及由此产生的固定维修费用的总和。表3所示为部件采用传统预防性维修策略的优化结果。 表3 传统预防性维修周期的优化结果 采用基于机会策略的列车转向架关键部件预防性维修决策模型,将机会维修策略加入传统预防性维修,并将表1和表2的数据带入模型进行优化,分析关键部件的机会维修时机和预防维修时机[14],结果如表4所示。 表4 机会维修优化结果 该模型的求解利用MATLAB R2012a编程实现,设置最大迭代次数为4 000,每个策略的编程求解过程独立,其模拟结果可以说明每个策略的维护成本。如图4和图5所示,采用机会维修策略时,维修费用为23.99元/d,低于传统预防性维修策略的维修费用,维修费用节省率为4.76%,且单位时间维修费用趋于稳定。 以该地铁公司30列B型车(采用4动2拖的列车编组)为例,每列车有轴承12对、轮对12对、轴箱24个、减震器8个,抗侧滚扭杆6根,则30列车一年可以节约维修费用约100.62 万元。 上述分析结果表明,采用机会维修策略的预防性维修模式更加节省维修费用。 初始化节点的启发信息λi、信息启发因子α、期望启发因子δ、信息素强度Q、信息素挥发因子ρ、算法迭代总次数Nmax、蚂蚁总数M[15]。 设置MMAS的参数:α=2,δ=3,Q=85,ρ=0.65,Nmax=100,M=10。运用MATLAB进行仿真,其迭代过程和次数如图6所示,算法在54次迭代时取得最优,此时的最佳机会维修阈值为0.03。当同一类关键部件个数R=10时,由图2平均费用率拓扑图构造算法流程和式(2)计算得关键部件的机会维修阈值如表5所示,与运用MMAS算法优化的最佳机会维修阈值基本相等。运用MMAS算法可以快速求解目标函数值,具有较强的鲁棒性和搜索最优解的能力。 表5 机会维修阈值优化结果 关键部件机会维修阈值平均机会维修阈值10.03120.02930.02940.03050.0290.029 6 对比表3和表4可知: (1)采用机会维修策略比传统的预防性维修周期策略节省维修费用4.76%。 (2)从关键部件最小费用的比较结果可以看出,当部件1在Δt1∈(284,318)天发生故障时,若部件2已工作Δt2∈(290,337)天,部件3已工作Δt3∈(303,342)天,部件4已工作Δt4∈(312,330)天,部件2,3,4与部件1组成的机会维修费用低于传统预防性维修费用,则部件1可进行与部件2,3,4组成的机会维修;当部件2在Δt2∈(290,337)天发生故障时,若部件3已工作Δt3∈(303,342)天,部件4已工作Δt4∈(312,330)天,部件5已工作Δt5∈(320,339)天,部件3,4,5与部件2组成的机会维修费用低于传统预防性维修费用,则部件2可进行与部件3,4,5组成的机会维修;当部件3在Δt3∈(303,342)天发生故障时,若部件4已工作Δt4∈(312,330)天,部件5已工作Δt5∈(320,339)天,部件4,5与部件3组成的机会维修费用低于传统预防性维修费用,则部件3可进行与部件4,5组成的机会维修;当部件4在Δt4∈(312,330)天发生故障时,若部件5已工作Δt5∈(320,339)天,部件5与部件4组成的机会维修费用低于传统预防性维修费用,则部件4可进行与部件5组成的机会维修。 (3)若某个部件发生故障的时机均不在上述的机会维修周期时间段,则按基于机会策略的故障维修模式执行维修。 (4)采用机会维修策略可以有效降低各个部件因故障而停止运营检修的次数,减少固定维修成本,从而适当延长预防维修周期,保证列车的在线运营率。 本文提出列车关键部件预防性维修决策优化模型,结合机会维修周期和预防性维修周期,以平均最小维修费用率为优化目标建立了机会维修策略优化模型。通过MMAS算法确定机会维修阈值,运用机会维修策略优化模型确定列车转向架关键部件执行机会维修策略的最佳机会维修和预防维修周期,机会维修策略考虑关键部件之间的维修周期和经济相关性,较好地解决了因各类维修而频繁停车、固定维修成本居高不下的问题,并可以有效减少列车在库停车检修时间和维修费用,提高列车的上线运行效率。 在后续的研究工作中将寻求更加高效的优化算法,进一步减少迭代次数,提高求解效率,探索人工智能与优化检修策略融合的方法,为列车关键部件检修提供技术支持。 参考文献: [1] GUO Xin, LI Chunguang, HUANG Ting, et al. Application of subway vehicle maintenance model[J]. Urban Mass Transit,2015,18(4):5-8(in Chinese).[郭 新,李春广,黄 挺,等.地铁车辆检修模式探讨[J].城市轨道交通研究,2015,18(4):5-8.] [2] SUN Chao, XU Yongneng. Optimum maintenance circle model for rail transit vehicle’s running gear[J]. Urban Mass Transit,2015,18(1):81-85(in Chinese).[孙 超,徐永能.城市轨道交通车辆走行部维修周期优化模型[J].城市轨道交通研究,2015,18(1):81-85.] [3] GUO Yunpeng, ZHAO Runsheng. Evaluation model of maintenance cycle of bogie for urban rail transit vehicle[J]. Electric locomotive and Urban Rail Vehicle,2017(1):21-24(in Chinese).[郭云鹏,赵润生.城市轨道交通车辆转向架维修周期优化模型[J].电力机车与城轨车辆,2017(1):21-24.] [4] WANG Lingzhi, XU Yugong, ZHANG Jiadong. Study on preventive maintenance optimization of multi-component system with reliability as center[J]. Computer Integrated Manufacturing Systems,2008,14(10):2042-2046(in Chinese).[王灵芝,徐宇工,张家栋.以可靠性为中心的多部件系统预防性维修优化研究[J].计算机集成制造系统,2008,14(10):2042-2046.] [5] WANG Lingzhi, XU Yugong, ZHANG Jiadong. Stability analysis model and application of key components of railway equipment[J]. Journal of the China Railway Society,2008,30(4):93-97(in Chinese).[王灵芝,徐宇工,张家栋.铁路设备关键零部件的可靠性分析模型及其应用研究[J].铁道学报,2008,30(4):93-97.] [6] JIN Yulan, JIANG Zuhua, HOU Wenrui. Optimization of preventive maintenance strategy for multi-component equipment with reliability as center[J]. Journal of Shanghai Jiao-tong University,2006,40(12):2051-2056(in Chinese).[金玉兰,蒋祖华,侯文瑞.以可靠性为中心的多部件设备预防性维修策略的优化[J].上海交通大学学报,2006,40(12):2051-2056.] [7] HAN Bangjun, FAN Xiumin, MA Dengzhe, et al. Uptical maintenance cycle model of manufacturing equipment by genetic algorithm[J]. Computer Integrated Manufacturing Systems,2003,9(3):206-209(in Chinese).[韩帮军,范秀敏,马登哲,等.用遗传算法优化制造设备的预防性维修周期模型[J].计算机集成制造系统,2003,9(3):206-209.] [8] TSAI Y T, WANG K S, TSAI L C. A study of availability-centered preventive maintenance for multi-component. systems[J]. Reliability Engineering &System Safety,2004,84(3):261-270. [9] HOU Wenrui, JIANG Zuhua, JIN Yulan. Multi-component system opportunity maintenance model based on reliability[J]. Systems Engineering and Electronics,2008,30(9):1805-1808(in Chinese).[侯文瑞,蒋祖华,金玉兰.基于可靠度的多部件系统机会维护模型[J].系统工程与电子技术,2008,30(9):1805-1808.] [10] NI Jun, GU Xi, JIN Xiaoning. Preventive maintenance opportunities for large production systems[J]. CIRP Annals-Manufacturing Technology,2015,64(1):447-450. [11] LAGGOUNE R, CDATEAUNEUF A, AISSANI D. Opportunistic policy for optimal preventive maintenance of a multi-component system in continuous operating units[J]. Computers & Cdemical Engineering,2009,33(9):1499-1510. [12] ZHOU Xiaojun, XI Lifeng, LI Jie. Preparation model of equipment sequential preventive maintenance based on reliability[J]. Journal of Shanghai Jiaotong University,2005,39(12):2044-2047(in Chinese).[周晓军,奚立峰,李 杰.一种基于可靠性的设备顺序预防性维护模型[J].上海交通大学学报,2005,39(12):2044-2047.] [13] ZHAO Hongshan, YAN Shengteng, LIU Jingqing. Optimal maintenance of wind turbine based on opportunity maintenance model[J]. Power Grid & Clean Energy,2012,28(7):1-5(in Chinese).[赵洪山,鄢盛腾,刘景青.基于机会维修模型的风电机组优化维修[J].电网与清洁能源,2012,28(7):1-5.] [14] CAI Jing, ZUO Hongfu, WANG Huawei, et al. Study on simulation of maintenance cost of complex system based on opportunity maintenance[J]. Journal of System Simulation,2007,19(6):1397-1399(in Chinese).[蔡 景,左洪福,王华伟,等.基于机会维修的复杂系统维修费用仿真研究[J].系统仿真学报,2007,19(6):1397-1399.] [15] WANG Zhongkai, SHI Tianyun, LIN Boliang, et al. Optimization model and algorithm for scheduling problem of high maintenance shop in EMU[J]. China Railway Science,2016,37(6):82-89(in Chinese).[王忠凯,史天运,林柏梁,等.动车组高级检修车间调度问题的优化模型及算法[J].中国铁道科学,2016,37(6):82-89.]3 求解算法
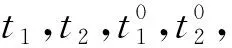
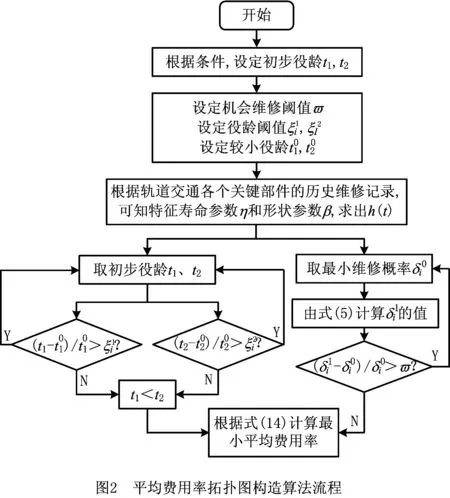

4 仿真分析
4.1 列车转向架关键部件参数

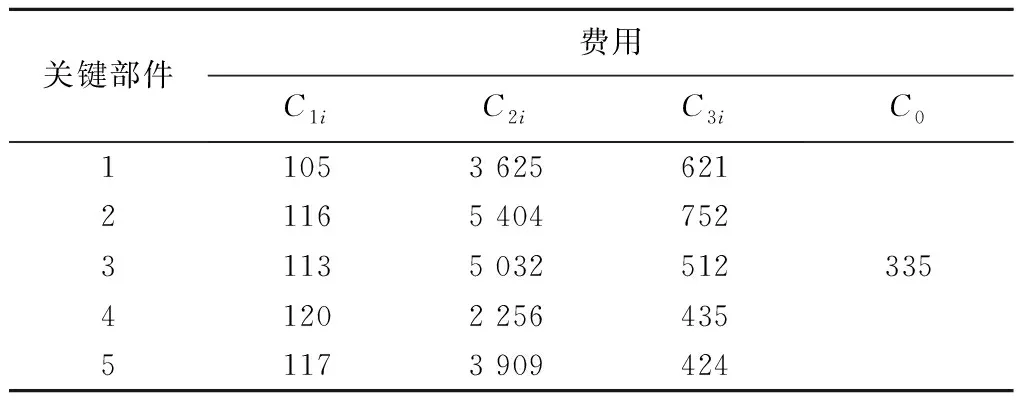
4.2 列车转向架关键部件预防性维修策略优化结果对比

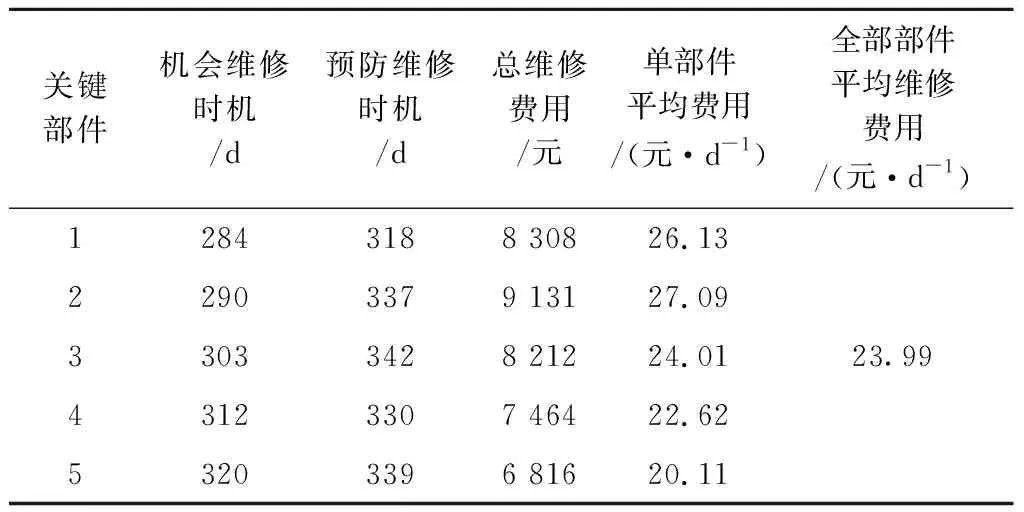
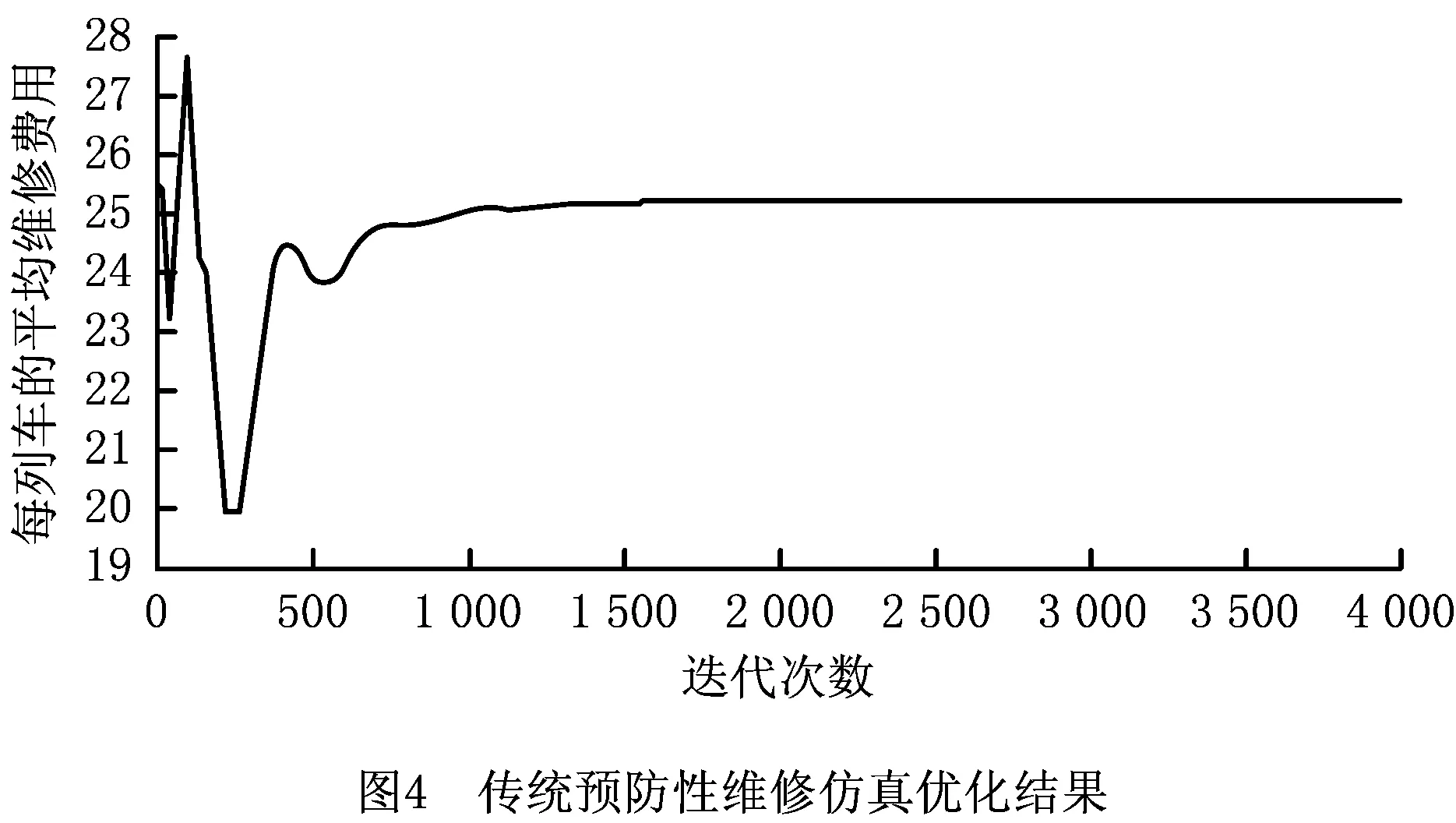
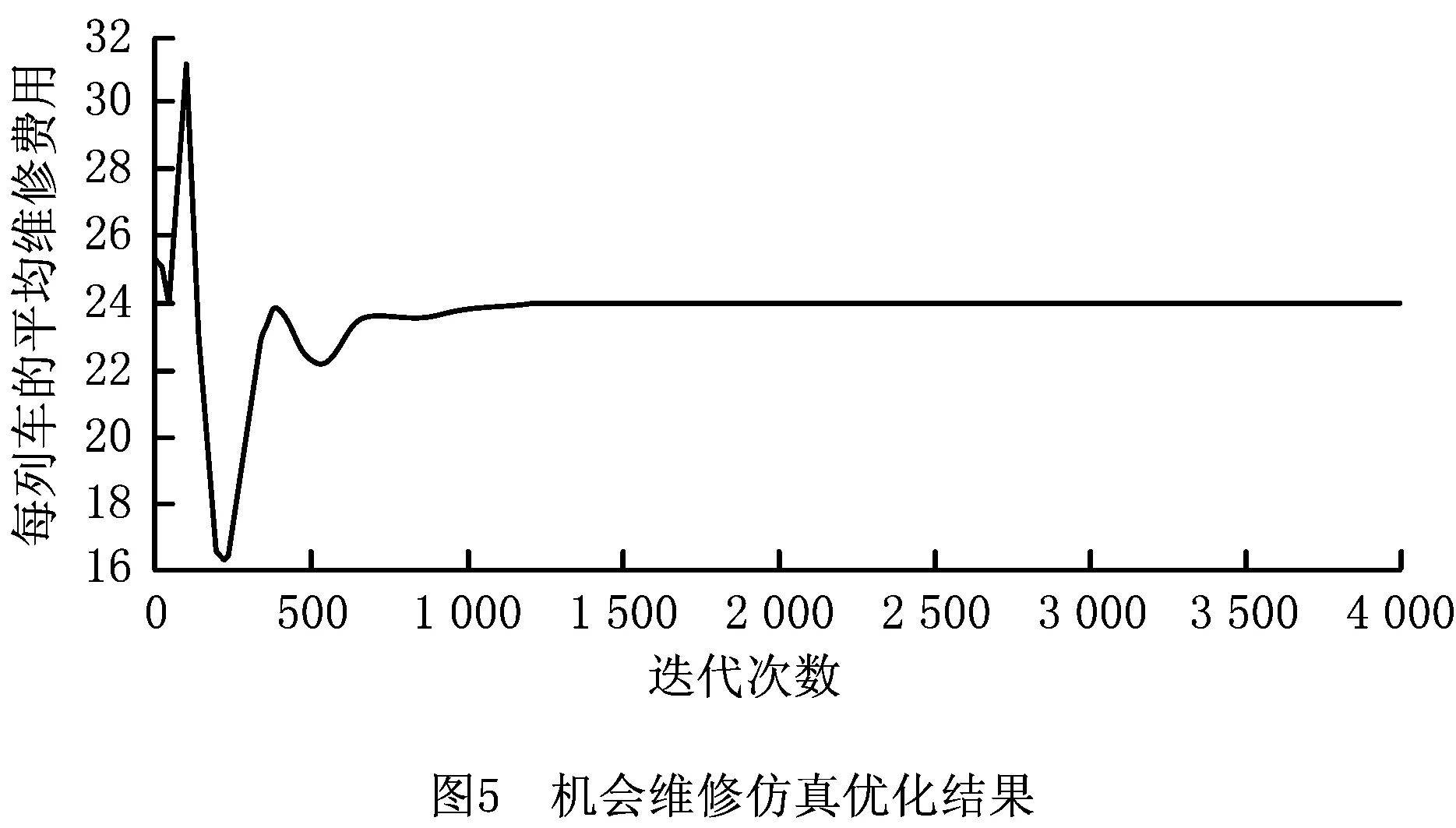
4.3 列车转向架关键部件机会维修仿真结果


4.4 结果分析
5 结束语

