研究性课题：欧拉公式的发现——教学设计

青海省海东市化隆回族自治县第一中学 王国昌

一、教材内容分析

人教版《全日制普通高级中学教科书（试验修订本•必修）•数学》第二册（下А）第九章9.9节研究性课题：多面体欧拉公式的发现。本节采用“研究性学习”的形式，注重强调发现的过程，有意识的培养学生探究问题的良好习惯，掌握一些研究问题的思想方法，并对提高协作能力具有重要的作用。

二、教学目标

1.知识目标：识记平面和多面体欧拉公式，了解公式的发现过程。

2.能力目标：了解数学概念和结论的产生过程，提高发现、提出、解决数学问题的能力；发展学生的创新意识和创新能力；进一步培养学生由特殊到一般的归纳猜想能力和逻辑思维能力以及人际交往协作能力。

3.情感目标：以平面和多面体欧拉公式的探索为载体，体验数学研究的过程和创造的激情，体验数学的简洁美和内在美，学习欧拉杰出的智慧、孜孜不倦的奋斗精神和严谨的科学态度。

三、教学重难点

1.重点：了解平面和简单多面体欧拉公式。

2.难点：领会公式发现过程的思想和方法。

四、学习者特征分析

高二学生已具备一定的数学基础，如平面几何的图形结构和性质，并在学完简单几何体之后进行的，对学生的能力层次要求不是太高。

五、教学策略选择与设计

⑴教材创新:①增加了平面欧拉公式V-E+F=1这一被教材所忽视的平面图形比长短曲直更本质的属性的探究；②涉及到图论（连通图等）的一些基本概念。

⑵教法设计：主要采用小组合作研究，进行主体式、启发式、对比式和直观演示法等。

⑶学法设计：由浅入深、模型及多媒体演示、分组讨论、特殊到一般、观察归纳等方法。

⑷教学基本形式

教师引导——学生讨论——再引导——再讨论——归纳总结。

六、教学环境及资源准备

1.教室或教学研究室。

2.相关几何模型和多媒体课件演示。

七、教学过程

1.介绍欧拉，引入课题

【教师活动】介绍欧拉：著名数学家欧拉（Euler，1707—1783），瑞士人。在数学家贝努利（Bernoulli）的赏识下开始学习数学，16岁就获硕士学位，毕生从事数学研究，他的论著几乎涉及18世纪所有的数学分支。他首先使用f(x)表示函数 ，首先用∑表示连加，首先用i表示虚数单位。在几何学中首先发现并证明了欧拉公式。数学中的欧拉方程、欧拉猜想、欧拉定理等有很多，其中一个特例：eiπ+1=0，它将数学里最重要的几个数字联系到了一起，两个超越数：自然对数的底e和圆周率π；两个单位：虚数单位i和自然数的单位1，以及被称为人类伟大发现之一的0。数学家们评价它是“上帝创造的公式”，反映了数学中的奇异美。

【学生活动】1.了解欧拉一生研究数学，对人类作出的巨大贡献。2.学习欧拉欧拉杰出的智慧、顽强的毅力、孜孜不倦的奋斗精神和崇尚科学道德精神。

【设计意图】在了解、学习欧拉的基础上，沿着他的足迹研究几何图形中的三要素:点、线、面之间数量关系的欧拉公式。

2.观察归纳，发现规律

（1）预备工作

【教师活动】指导学生分组，达到组间同质、组内异质。

【学生活动】小组分工：选出组长、计时员、记录员、发言人。

【设计意图】体现教师的主导作用和学生的主体作用。

【教师活动】问题：①三角形内角和等于多少？（简称180°定理）；②三角形顺着一个方向的外角之和等于多少?③凸n边形内角和公式是什么?顺着一个方向的外角之和又如何?

【学生活动】讨论：①如何用图形语言演示或作图？用字母符号语言证明的思路？②证明用到哪些知识点? 证明的思想方法有哪些？③凸n边形内角和公式是什么？顺着一个方向的外角之和是多少？

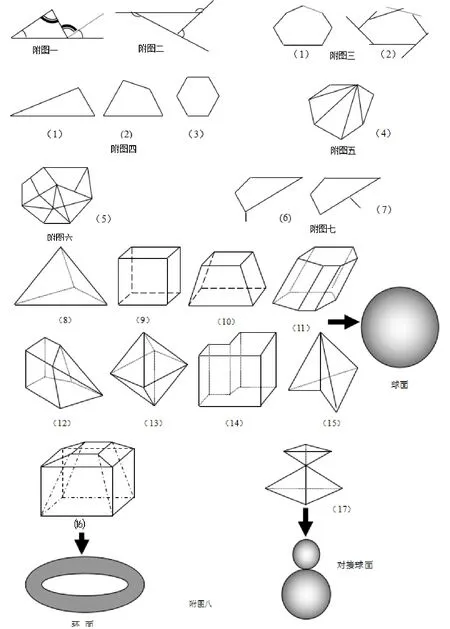
【设计意图】①一组代表演示，教师动画总结（附图一）；二组代表证明，教师补充归纳（动画一）。

②借助180°定理，平角及互补角概念，:三组代言人证明(附图二)，得出结论360°

③指导四组代表证明，教师总结(附图三)，结论：内、外角和分别为：（n-2）180°、360°。

（2）平面欧拉公式的探索

附表一

【教师活动】我们从浅显易懂的180°定理出发逐步探究欧拉公式。设平面上封闭图形中的所有不交的区域都是多边形。则分析这类图形的顶点数V， 边数E，区域数（面数）F之间的关系。

【学生活动】讨论：①凸n 边形的情况（附图四）；

②将凸n边形用不交的对角线剖分成若干个三角形（附图五）；

③平面封闭图形(图中所有不交的区域都是多边形)（附图六）；

④连通图：指从图中任何一点出发，沿着边可到达任何顶点的图形（附图七）。

【设计意图】四组代表填写附表一，突显学生的主体作用。

（3）简单多面体欧拉公式的探索

附表二

?

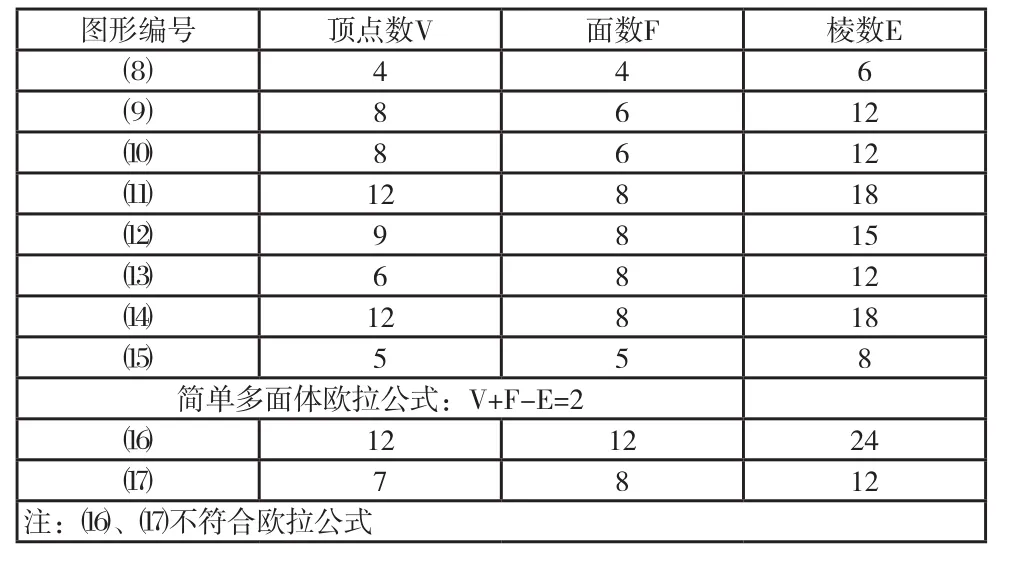
【教师活动】依次出示附图八中｛（8）～（13）、（14）～（15）、（16）～（17）｝各组图形或模型，要求学生研究V，E，F之间的关系。

【学生活动】①观察、分析各组图形或模型，填写表格，讨论、猜想有什么规律?②探索、归纳、总结，五组代表填写附表二。

（4）欧拉的创新思想和方法

【教师活动】欧拉研究多面体的方法：假设它的面是用橡胶薄膜做成的，然后充气，就会连续(不破裂，不粘连)变形(拓扑)，把它变成了曲面。（充气动画演示二）

【学生活动】比较图八中的图形。其中哪些多面体的表面能够连续(不破裂，不粘连)变形，最后其表面可变成一个球面?环面?两个对接球面?

【设计意图】①除图八(16)会变成一个环面，图八(17)会变成两个相切的球面外，其余的都变成球面。

②任何创新成果的产生都是以观念的创新和方法的创新为前提的。

八、课堂小结

1.有关定义：

定义⑴．多面体 (Polyhedron)以及面(Face)、棱(Edge)、顶点(V )。

定义⑵．连通图是指从图中任何一点出发，沿着边可到达任何顶点的的图形。

定义⑶．表面经过连续变形能变为一个球面的多面体叫简单多面体。

2.欧拉公式

⑴平面图形（连通图）的欧拉公式：V-E+F=1；

⑵简单多面体的欧拉公式：V-E+F =2。

3.欧拉的创新思想和方法

九、布置作业 预习欧拉公式的证明及应用。

十、评价形式（以指导、鼓励性评价为主）

组内评价：参与度、态度、积极性等。组间互评：思路、表述、方法等。

教师总结性评价：分工、表格设计、多元评价是否到位等。

十一、教学反思

教学中注意的问题：教师引导而不包办探究过程，注重强调发现的过程，通过分组讨论，逐步培养学生观察分析、由特殊到一般、归纳猜想的数学思想方法，并提高合作、探究的能力。

附图：