基于SSIM的自适应样本块图像修复算法

何 凯，牛俊慧，沈成南，卢雯霞



基于SSIM的自适应样本块图像修复算法

何 凯，牛俊慧，沈成南，卢雯霞

(天津大学电气自动化与信息工程学院，天津 300072)

现有基于样本块的图像修复算法，大多通过人工设定样本块大小来达到最佳修复效果，缺乏自适应性；此外，对图像不同纹理和结构区域采用相同大小的样本块，也不利于获得整体最优修复效果．为解决上述问题，本文提出一种基于改进结构相似性的自适应样本块大小选取算法，在传统的SSIM算法的基础上增加了梯度信息，并通过结合样本块亮度、对比度和结构3个模块来衡量结构差异，以此确定不同结构和纹理区域的最优样本块大小，提高算法适应性，改善修复效果．仿真实验结果表明，当图像存在复杂的结构和纹理信息时，本文算法仍然能够获得理想的修复效果．

图像修复；纹理合成；自适应样本块；SSIM算法；梯度信息

图像修复是计算机图像和视觉研究领域的热点之一，在文物保护、影视制作、老照片修复、目标移除等方面都得到了广泛的应用．其核心思想是利用图像中已知的纹理和结构信息，按照一定的修复顺序和匹配准则对缺损区域进行修补，以保证图像的视觉完整性．图像修复算法可以大致分为两大类：基于偏微分方程的图像修复算法和基于样本块的纹理合成算法．前者适用于小区域图像修复，后者可用于较大破损区域的修复，能够获得比较自然的纹理和结构修复效果．

本文主要针对第2类算法开展相关研究．目前，国内外学者已经提出了许多纹理合成算法，例如：Luo等[1]对经典的Criminisi算法[2]进行了改进，于2009年提出了基于深度图像的图像修复算法，将深度图像绘制和视点变化技术引入图像修复领域．2010年，Xu等[3]提出利用待修复块和邻域块的非零相似稀疏性来获得结构可信度，改进了修复顺序；此外，在信息填充过程中，将所得候选块的线性组合作为填充信息填充到破损区域．同年，Anamandra等[4]对优先权函数公式做了修改，加入了梯度及其对应的对数值，取得了不错的图像修复效果．2011年，Li等[5]采用小波变换法来检测图像的不完整凸结构，并运用线性拟合对基于样本块的纹理合成算法进行了改进．Cao等[6]使用结构张量来确定修复顺序和匹配准则，并利用K-最近邻域算法，有效减少了搜索最优匹配块的计算量．Smith等[7]设计了具有互斥鉴别特性的字典对来改进稀疏形态成分分解法，可以更好地提取图像的纹理和结构信息．Huang等[8]为解决因场景透视而产生的结构不连续问题，引入了仿射变换矩阵，利用图像中的消失点和线等信息，实现样本块的几何变换，有效提高了结构图像的修复效果．

此外，Zhou等[9]加强了数据项与结构信息之间的联系，对数据项做了加权处理，在结构边缘的保持方面取得了较好的处理效果．Sairam等[10]利用信息地图技术确定样本块修复准则，通过纹理生成技术解决图像丢失信息问题，取得了较好的修复效果．He 等[11]在KD-tree的基础上进一步完善了块匹配传播效果，提高了算法运行效率．Li等[12]改进了置信度计算公式，并提出了一种修复块相邻区域内的搜索方法，能有效缩小搜索范围，提高运行效率．2013年，谢琼等[13]提出了一种新的基于模式相似性的修复算法，利用了纹理的亮度变化规律和空间域的特性来确定最优匹配块，获得了不错的修复效果．Rodriguez-Sánchez等[14]利用角点冗余检测，借助非下采样轮廓波变换来改进置信度计算公式，并在获取最优匹配块的过程中使用了累计色散的方法，改善了修复效果．

此外，Zhou等[15]根据已知的邻域结构信息，提出了一种自适应确定样本块大小的算法，提高了算法的自适应性．2012年，孟春芝等[16]对该算法进行了改进，通过计算基于破损区域领域中完好部分的梯度值变化来确定最优样本块大小，提高了准确性，但算法需要考虑0°～360°梯度域数值，运算效率受到限制．为解决上述问题，本文提出一种基于改进SSIM算法的自适应样本块大小选取方法，在原有亮度、对比度和结构3个模块的指标的基础上增加了梯度信息，以此来衡量结构相似度．仿真实验结果表明，本文方法可以获得更加自然的结构修复效果．

1 基于样本块修复算法

基于样本块的图像修复算法主要包含以下3个步骤．

步骤1 确定待修复样本块的优先级．

 (1)

 (2)

步骤2 搜寻最佳匹配块并进行信息填充．

在信息完好区域寻找与待修补块相似度最高的样本块，并将其复制到破损区域当中．

步骤3 更新置信度．

更新像素点的置信度，进行下一次迭代，直到图像修复完成为止．

2 本文算法

传统基于样本块的图像修复算法，需要根据实验结果手动调整样本块大小，以获得最优修复效果．样本块偏小，算法效率低，也不利于保持图像的整体结构；反之，容易出现结构断裂的现象，纹理修复效果不理想．此外，采用固定大小样本块对不同的结构和纹理区域进行处理，缺乏适应性，当图像结构和纹理情况复杂时，不利于获得理想的修复效果．为此，本文提出一种基于改进SSIM算法的自适应样本块大小确定方法，可以根据不同的结构和纹理区域自适应选取样本块大小，提高了算法适应性，可以获得理想的图像修复效果．

2.1 结构相似性度量

结构信息能够反映图像之间的差异，可以用于图像识别．其中，结构相似度(SSIM)[17]可以获取符合人眼视觉系统的图像结构信息，得到了广泛应用．传统SSIM定义为

 (3)

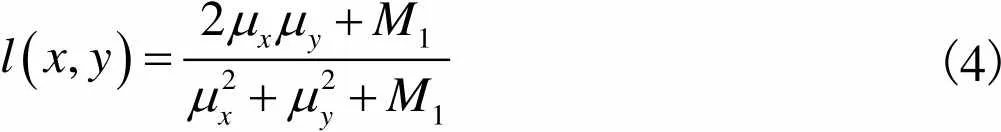
 (4)

 (5)

 (6)

2.2 样本块大小自适应选取

本文尝试将待修复样本块大小选取问题转化为结构相似性度量问题，利用改进后的SSIM算法实现样本块大小的自适应选取．原始SSIM算法通常利用结构分量来表征局部区域的结构差异，本文在原有SSIM算法的基础上引入梯度信息，以实现图像局部边缘及纹理的量化表征．由于破损区域存在信息缺失，因此，本文利用破损块对应的原图像块来计算相关梯度信息．

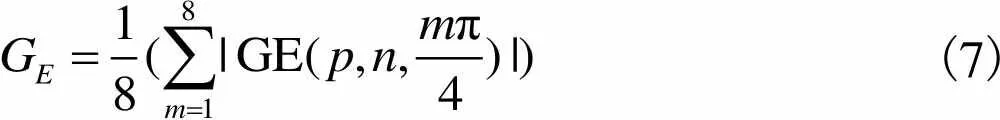
 (7)

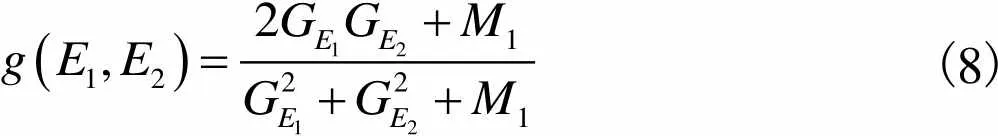
 (8)

结合梯度信息，本文定义区域结构相似度的 RSS为

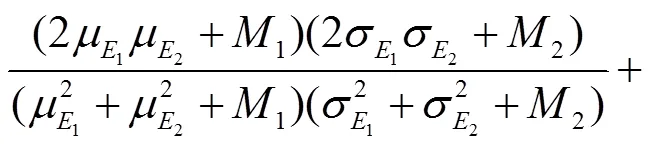
(9)

当待修复区域的结构变化比较单一时，相邻尺寸样本块之间结构结构相似度较高，RSS值较大，此时应选取较大的样本块进行修复，以保证修复效率；而当待修复区域结构信息比较复杂时，相邻尺寸样本块之间的结构相似度较低，RSS较小，此时应选取较小的样本块，以保证结构的有效延续．为此，本文定义样本块大小选取方法为

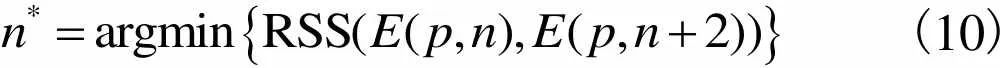
 (10)

在实际修复过程中，当源匹配块位于图像边缘时，此时可能存在样本块不完整的情况，为此，本文定义源匹配块与待匹配块之间的误差限制准则为

 (11)

2.3 本文算法流程

本文算法流程如下．

步骤4 根据最小绝对差平方和算法(SSD)[2]在图像信息完好区域搜索最优匹配块，计算匹配误差．

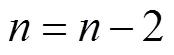
3 实验结果及分析

为了对算法性能进行比较，选取了几幅具有不同结构和纹理类型的自然场景图像，利用Non-Local算法[18]、Parabola算法[19]和Meng算法[16]分别进行处理．Non-Local算法通过引入变分框架来对图像进行修复；Parabola算法改进了置信度与数据项的权重系数和置信度更新公式；Meng算法运用梯度域进行自适应修复；其图像效果分别如图1所示．

从图1可以看出，采用变分框架的Non-Local算法，虽然成功修复了海水轮廓，但由于样本块大小无法自适应选取，在连接处出现了折叠和模糊．Parabola算法虽然在一定程度上抑制了置值度函数迅速下降的情况，但当破损区域较大时，出现了明显的断层．Meng算法能够自适应选择样本块，修复效果优于前面2种算法，但仍然存在人工痕迹．本文算法基于图像结构相似度，并结合梯度信息，海水纹理扩散更加合理，结构修复效果也更加自然．

图1 图像Beach修复效果比较

图2破损图像包含大区域复杂结构和纹理信息．从图中可以看出，利用Non-Local算法的变分模型恢复的台阶边缘不够清晰；与之类似，Parabola算法在结构传播方面也存在问题；Meng算法依据梯度域评测图像结构相似度，在纹理和结构保持方面不够理想；而本文算法不仅完整的恢复了台阶结构，纹理修复效果也更加自然合理，取得了理想的处理效果．

图2 图像Stairs修复效果比较

由表1可以看出，Non-Local算法的处理时间最短，本文方法其次，且明显优于另外2种算法；然而，利用Non-Local算法对结构进行修复，容易出现模糊和断层现象，相比之下，本文算法不仅运算速度较快，修复效果也更加自然合理，整体效果最优．

表1 图像修复时间

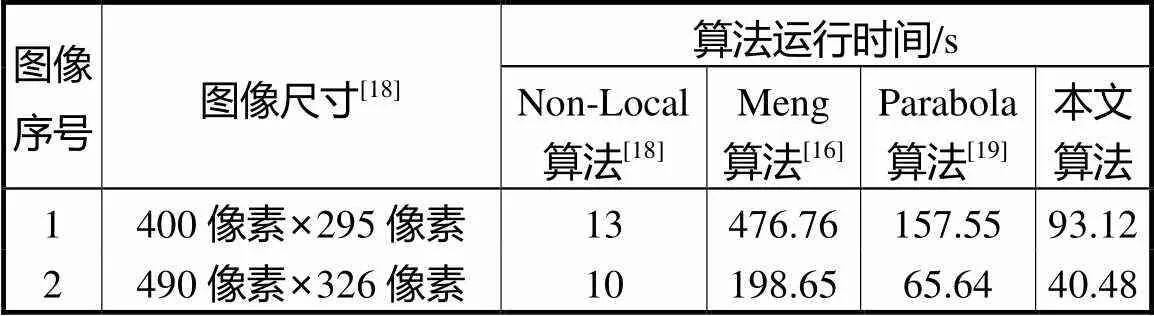
Tab.1 Time of image inpainting

4 结 语

本文提出了一种基于改进结构相似度测量的自适应样本块图像修复算法，可以根据图像局部结构信息，自适应确定样本块大小，提高了算法的适应性和修复效果．仿真实验结果表明，本文算法对于复杂的结构和纹理图像，仍然能够获得理想的修复效果．

［1］ Luo K，Li D，Feng Y. Depth-aided inpainting for disocclusion restoration of multi-view images using depth-image-based rendering[J].：，2009，10(12)：1738-1749.

［2］ Criminisi A，Perez P，Toyama K. Object removal by exemplar-based inpainting[C]//2003. Wisconsin，USA，2003：721-728.

［3］ Xu Zongben，Sun Jian. Image inpainting by patch propagation using patch sparsity[J].，2010，13(9)：1200-1212.

［4］ Anamandra S H，Chandrasckaran V. Exemplar-based color image inpainting using a simple and effective gradient function[C]//. Las Vegas，USA，2010：140-145.

［5］ Li S，Zhao M. Image inpainting with salient structure completion and texture propagation[J].，2011，32(9)：1256-1266.

［6］ Cao F，Gousseau Y，Masnou S，et al. Geometrically guided exemplar-based inpainting[J].，2009，4(4)：1143-1179.

［7］ Smith L N，Elad M. Improve dictionary learning：Multiple dictionary updates and coefficient reuse[J].，2013，20(1)：9-28.

［8］ Huang J B，Kang S B. Image completion using planar structure guidance[J].，2014，33(4)：129-1-129-10.

［9］ Zhou Yatong，Li Lin. Research on weighted priority of exemplar-based image inpainting[J].，2012，29(1)：166-170.

［10］ Sairam V，Sarma R R，Balasubramanian S，et al. A unified framework for geometry and exemplar based image inpainting[C]//2. Paris，France，2014：511-515.

［11］ He Kaiming，Sun Jian. Computing nearest-neighbor fields via propagation-assisted KD-trees[C]//2012. Providence，USA，2012：111-118.

［12］ Li Zhangming，Hu Wenjin. A novel method for exemplar-based image inpainting[J].，2012，9(3)：761-769.

［13］ 谢 琼，张红英，彭 博. 基于模式相似性的图像修复算法[J]. 现代电子技术，2013，36(2)：94-96.

Xie Qiong，Zhang Hongying，Peng Bo. Image inpainting algorithm based on pattern similarity[J].，2013，36(2)：94-96(in Chinese).

［14］ Rodriguez-Sanche Z，Garcfa J A，Fdez-Valdivia J. Image inpainting with nonsubsampled Contourlet transform[J].，2013，34(13)：1508-1518.

［15］ Zhou H L，Zheng J M. Adaptive patch size determination for patch-based image completion [C] //201017. Hong Kong，China，2010：421-424.

［16］ 孟春芝，何 凯，焦青兰. 自适应样本块大小的图像修复方法[J]. 中国图像图形学报，2012，17(3)：337-341.

Meng Chunzhi，He Kai，Jiao Qinglan. Image completion method with adaptive patch size[J].，2012，17(3)：337-341(in Chinese).

［17］ Wang Z，Bovik A C，Sheikh H T，et al. Image quality assessment：From error cisbility to structural similarity [J].，2004，13(4)：600-612.

［18］ Vadim F，Gabriele F，Pablo A，et al. Variational framework for non-local inpainting[J].，2015，5：362-386.

［19］ Nan A，Xi X. An improved Criminisi algorithm based on a new priority function and updating confidence[C]//2014 7. Dalian，China，2014：885-889.

(责任编辑：王晓燕)

Image Inpainting Algorithm with Adaptive Patch Using SSIM

He Kai，Niu Junhui，Shen Chengnan，Lu Wenxia

(School of Electrical and Information engineering，Tianjin University，Tianjin 300072，China)

The current exemplar-based algorithms lack adaptability due to manually determining the size of block．In addition，using a patch with the constant size is not suitable to obtain the optimal effect in different structure and texture regions．To address this problem，this paper puts forward an adaptive patch size selection method using improved structure similarity(SSIM)．The gradient information is added to the traditional SSIM and is combined with the brightness，contrast ratio，and structure of patch to measure the structural difference．On this basis，the optimal size of patch in different structure or texture regions is determined，thus improving the adaptability，as well as the inpainting effect．The simulation results demonstrate the effectiveness of the proposed method even when complex structure or texture exists.

image inpainting；texture synthesis；adaptive patch；SSIM algorithm；gradient information

10.11784/tdxbz201704066

TP391

A

0493-2137(2018)07-0763-05

2017-04-23；

2017-09-26.

何 凯（1972—），男，博士，副教授

何 凯，hekai@tju.edu.cn.

国家自然科学基金资助项目(61271326).

the National Natural Science Foundation of China(No.,61271326).