大型冷却塔考虑多种风载荷分布模式的结构优化选型
赵 林, 王志男, 梁誉文, 葛耀君
(同济大学 土木工程防灾国家重点实验室, 上海 200092)
0 引 言
大型冷却塔结构对于风载荷作用较为敏感[1]。1965年,英国渡桥电厂八塔组合中三座位于背风区的冷却塔发生风致倒塌,风致干扰效应引起了人们的极大重视。我国规范[2-3]采用群塔比例系数考虑风致干扰效应,冷却塔塔筒模板的基于规范二维等效静力载荷条件下配筋率通常需大于风洞试验风压设计的包络配筋,较少在满足安全性的同时兼顾经济性。至于冷却塔结构设计的优化,设计院大多采用试算结构构件设计尺寸的控制变量法结合穷举算法[4-5],效率低下,并非真正的结构优化设计。冷却塔向大型化发展,塔群组合也趋于复杂[6],现有的结构优化设计愈加难以满足发展的趋势。冷却塔考虑群塔干扰效应的结构设计优化,通常需包括两个环节:首先需要确定复杂干扰条件下,哪一种风载荷作用模式为可能的最不利载荷模式;在此基础之上引入响应面法和梯度搜索法,优化潜在最不利载荷条件下整体结构刚度协调分配,进而获得优化的结构构件尺寸。受困于气动力载荷作用的多样性和整体结构优化算法的复杂性,即风载荷众多抗风设计等效准则,缺少统一的想法和理念,且结果差异明显[7-11]。1962年,Csonka[12]推导了双曲线壳体的壁厚变化公式,使结构在自重作用下能合理使用材料。20世纪60年代末,Konstruktiver[13]对某120 m高冷却塔方案进行综合投资、材料消耗和结构安全度的比选中发现,适当的子午线形状可获得经济的塔形,且几何尺寸微小的变化就有明显的效果。1971年,Coll[14]在IASS上提出冷却塔壳体优化的观点:以合理的最小筒壁厚度保证稳定性,以合适的子午线形状得到最小总重。1972年,Greiner-Mai和Auerbach[15]从力学和工艺观点研究了子午线形选择问题,开始考虑冷却塔的形状与功能、承载能力、投资之间的关系。上述研究[12-15]多采用方案比选的方式,呈现了塔筒少数参数对结构经济性、稳定性或安全性的影响,以下学者的研究采用优化算法进行结构多参数优化。2006年,Lagaros[16]引入进化策略进行基于可靠度的结构优化设计,以非确定分析得到的屈曲失效概率和确定性分析得到的单元Mises应力为约束。2007年,Uysal[17]采用线性规划法优化壳体质量,以单元Mises应力为约束条件。2011年,张宗方[18]采用二次规划法分别进行了基于质量和塔筒最大拉应力的优化,约束源于我国规范对优化变量上下限和稳定系数的要求,并以单元单轴和三轴应力检验强度安全。2015年,Rumpf M[19]对混凝土薄壳结构几何外形、局部截面厚度进行优化,基于总质量、位移、应变等目标,进行多方案比选。2015年,Wu Y[20]采用梯度搜索法和模式搜索法对结构形状与尺寸进行优化,以最小应变能和自重为优化目标(见表1)。上述学者[16-20]的研究多以结构效应(内力或位移效应)为优化目标,存在优化目标准则的非唯一性,难于明确多种优化策略的经济性指标;常用优化过程仅聚焦于上部结构塔筒线形和结构尺寸的优化,忽略下部结构对整体结构性能的影响;约束条件多采用局部失稳公式验算稳定性[21-26],没有基于整体结构,且缺少对于结构强度问题的考虑,这种得出的优化结论容易以偏盖全。

表1 冷却塔结构优化选型研究工作一览Table 1 Summary sheet of structural optimization for cooling towers
针对上述问题,本文定义内力组合加权效应(配筋量)和经济造价为综合效应指标,聚焦多种优化策略的经济性指标,兼顾结构强度安全性,实施了冷却塔抗风设计的分阶段优化设计策略。首先,实现了双曲线型冷却塔的参数化和有限元分析结合,然后将稳定系数、构件配筋率和总造价确定为衡量塔筒稳定性、强度安全性(结构受力合理性)和经济性的量化指标;而后,确定优化目标及约束条件,利用响应面法与梯度搜索算法进行结构优化选型。优化适用于不同的风载荷分布模式的塔型,并以初始塔型为参照,对比各最优塔型的塔筒稳定性、强度安全性和经济性,采用交叉检验方式,最终推荐最优化塔型。研究工作思路见图1。
1 最不利风载荷模式
1.1 群塔组合风洞试验
以六塔组合试验作为验证,说明考虑塔群干扰效应的最不利风载荷获得依据。群塔干扰刚性模型风洞测压试验在同济大学土木工程防灾国家重点实验室TJ-3风洞中进行,见图2。冷却塔实际塔高为250m,支柱底部直径191.8m,缩尺比为1:200,。利用美国SCANIVALUE公司的DSM3000电子式压力扫描阀系统、信号采集测控系统获取冷却塔表面风压信号,采样频率为300 Hz,采样时长为40 s。测压孔沿模型外表面子午向、环向布置12×36=432个,即沿塔筒高度布置12层测压孔,每层沿环向以10°为间隔均匀布置36个测压孔。干扰效应受塔位布置、
风向和塔间距的影响,本试验沿环向以22.5°间隔分布共16个风向角,塔群采用矩形(Rec)和菱形(Rho)两种布置形式,中心距L分别为1.5D、1.75D、2.0D。风向角定义、塔位布置见图3、图4,图中每座塔的风向角均按图4(c)定义,菱形布置1.5D间距1号塔0°风向角可定义为Rho_1.5D_T1_0°,以此类推。试验中利用尖劈和粗糙元模拟B类地貌大气边界层湍流风场,采用“三、四层交替粘贴纸带+10m/s试验参考风速”的手段进行雷诺数效应模拟[27]。
(a) 测压孔布置(单位:mm)
(b)测压塔模型和流场布置
图2测压塔尺寸和模型图
Fig.2Layoutofpressuretapsandthecoolingtowermodel
1.2 典型风载荷分布模式
所有风洞测压试验工况共241个,见表2。涉及3种塔位布置形式、3种塔间距、16个风向。定义载荷、响应、配筋层面的25种群塔比例系数K[28],见表3。
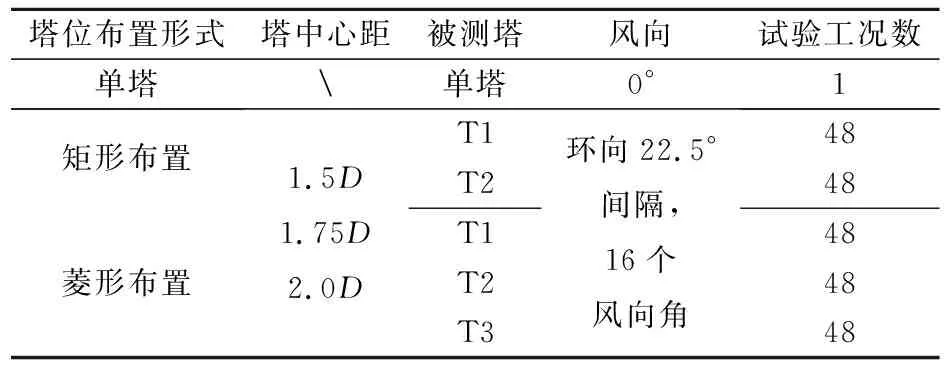
表2 风洞测压试验工况Table 2 Wind tunnel test cases

表3 群塔比例系数定义说明Table 3 Symbols and physical meanings of definition criteria
K=Ix/Is
(1)
式中,K为群塔比例系数,IX为某特征量在群塔组合中所有塔在所有风向的最值,IS为该特征量的单塔值。
基于任一特征量定义的群塔比例系数都难以确切描述实际干扰效应导致的复杂风压分布变化[29]。鉴于此,根据25种群塔比例系数最大值出现的频率、塔位布置形式、塔相对位置,筛选出相应工况的塔筒表面三维风压作为典型风载荷分布模式,即最不利风载荷。为探究最不利工况,表4统计了25种群塔比例系数最大值及其对应工况并将其频率分布以饼状图的形式表示(见图5),菱形和矩形布置形式出现的频率分别为88%、12%,说明菱形布置较矩形不利。
在25个最大值中,Rho_1.75D_T1出现的次数最
大,共9次,其不利风向角89%(8次)为315°;Rho_1.5D_T2出现的次数次之,共4次,其不利风向角50%(2次)为90°;其它情况的最大值都出现在分散的风向角。选取Rho_1.75D_T1_315°工况(频率为32%)、Rho_1.5D_T2_90°工况(频率为8%),结合六塔组合的塔位布置,同时选取Rec_1.5D_T1_0°工况,将这3种工况对应的风洞试验平均风压系数及规范模式二维对称风压作为六塔组合的典型风载荷分布模式,并依据“通道”气流加速效应、“屏蔽”载荷降低效应、风压对称性给三种风载荷分布模式命名,见表5。

群塔比例系数编号最大值对应工况布置形式塔间距塔位风向角11.47菱形1.50D1#塔315°21.59矩形1.75D1#塔337.5°31.22菱形2.00D3#塔45°41.35菱形2.00D1#塔337.5°51.17菱形1.75D1#塔315°61.17菱形1.75D1#塔315°71.15菱形1.75D1#塔315°81.15菱形1.75D1#塔315°91.12菱形1.50D2#塔90°101.11菱形1.50D2#塔90°111.11菱形1.75D1#塔315°121.18菱形1.75D1#塔315°131.19矩形2.00D1#塔337.5°141.18菱形1.75D1#塔315°141.13菱形2.00D3#塔90°161.30菱形1.75D3#塔67.5°171.20菱形2.00D1#塔337.5°181.29菱形1.75D3#塔90°191.28菱形1.50D2#塔135°201.36菱形1.75D1#塔315°211.71菱形1.50D1#塔315°221.11矩形1.75D1#塔270°231.26菱形1.75D1#塔90°241.36菱形1.50D2#塔202.5°251.18菱形1.50D3#塔112.5°

表5 典型风载荷分布模式Table 5 Typical adverse wind load patterns
1.2.1 规范模式二维对称风压
对于试验单塔工况,根据塔筒表面平均风压系数的分布(图6a),可将塔筒沿环向分为迎风区(330°~30°)、侧风区(30°~120°、240°~330°)、背风区(120°~240°)。风压沿塔筒壁垂直向内作用(风压为正),最大平均风压系数出现在0°(即来流方向)位置,自此平均风压系数沿环向向两侧递减。在侧风区,风压沿塔筒壁垂直向外作用(风压为负),在70°、290°位置负压最大。在背风区,风压为负,分布均匀,平均风压系数在-0.5左右。试验单塔工况塔筒风压基本呈对称分布,与水工规范平均风压相比,其差异主要存在于端部,表现在侧风区和背风区平均风压系数较小。对单塔而言,可用规范模式二维对称风压进行设计,群塔比例系数取1.3,源自表3中25种干扰准则分别获得比例系数最大值的平均值。
1.2.2 遮挡干扰三维非对称风压
对于Rec_1.5D_T1_0°工况(图6b),由于2号、3号塔对1号塔的“屏蔽”载荷降低效应,使1号塔的平均风压系数极值较水工规范的有较大降低。上风区两排冷却塔形成的“通道”气流加速效应导致1号塔塔筒迎风、侧风区风压分布呈现严重的不对称。屏蔽载荷效应占主导,将此风载荷分布模式称之为遮挡干扰三维非对称风压。
1.2.3 试验等效三维非对称风压
对于Rho_1.75D_T1_315°工况(图6c),平均风压系数极值较水工规范的有较大增长。塔筒风压在迎风区基本对称分布,其不对称性主要出现在侧风区,这是1号塔受到上风区2号塔的“通道”气流加速效应引起的。将此风载荷分布模式称之为试验等效三维非对称风压。
1.2.4 通道加速气流三维对称风压
对于Rho_1.5D_T2_90°工况(图6d),平均风压系数极值较水工规范的有较小增长,平均风压系数负极值(20°、160°)较试验单塔工况的有较大增长,这是2号塔受到上风区对称分布的4号、5号塔的“通道”气流加速效应导致的。塔筒风压基本呈对称分布,因“通道”气流加速效应整体放大,将此风载荷模式称之为通道加速气流三维对称风压。

拟合参数遮挡干扰三维非对称风压下部中部上部试验等效三维非对称风压下部中部上部通道加速气流三维对称风压下部中部上部水工规范全高度a0-0.340-0.349-0.340-0.659-0.651-0.572-0.452-0.535-0.477-0.443a10.4010.2610.2340.4660.3100.4000.4790.3800.4400.245a20.4160.4280.3060.6780.7210.6940.6510.7200.6960.675a3-0.0130.0640.0180.3950.5730.4600.2680.4150.3370.536a4-0.157-0.184-0.1070.1140.1330.0690.016-0.017-0.0300.062a5-0.014-0.051-0.013-0.007-0.102-0.072-0.014-0.087-0.069-0.138a60.0430.0610.0230.058-0.0150.0200.0340.0170.0340.001a7-0.0180.005-0.0090.0030.0280.0470.0410.0370.0450.065b1-0.017-0.018-0.0100.0610.0620.019-0.047-0.157-0.139/b20.0150.0340.0330.0060.0020.0040.0720.0790.063/b30.0230.0800.053-0.007-0.0080.020-0.121-0.013-0.006/b40.0350.0620.0260.000-0.0150.016-0.143-0.094-0.080/b50.0150.001-0.007-0.009-0.009-0.001-0.003-0.044-0.023/b60.012-0.010-0.003-0.018-0.008-0.0090.0310.0640.042/b70.0100.0050.0050.000-0.004-0.006-0.0210.0150.012/
考虑复杂群塔干扰条件下的冷却塔抗风设计需要采用典型最不利风载荷分布模式,将三种试验风载荷分布模式用傅里叶展开式拟合,考虑到塔筒进风口和出风口的典型三维分布特征,对塔筒下部(≤0.3H)、中部(介于0.3H和0.8H之间)、上部(≥0.8H)的平均风压分布曲线分别模拟,拟合参数结果见表6。以遮挡干扰三维非对称风压的拟合结果(图7)说明,拟合曲线相比于水工规范正负压峰值均明显下降,正、负压极值所在点均向背风区偏移,背风区缩短;且随着高度增加,风压沿环向分布趋于平缓,三维分布特性显著。这种与规范二维风压分布截然不同的风载荷分布模式对冷却塔抗风设计的影响需审慎评估。限于篇幅,另外两种风载荷分布模式仅给出拟合参数(表6)。
(2)
2 结构优化
2.1 优化目标、算法和约束条件
获得最不利风载荷分布模式后,进行结构优化设计。优化目标为找到适用于四种风载荷分布模式的最优塔型方案,以总造价主导优化过程,同时以构件配筋率和稳定系数兼顾安全性和稳定性。
已有的研究其优化目标多为壳体质量或结构效应,优化目标不唯一,难以明确优化策略的经济性;或有研究关注经济性,但仅聚焦于壳体的材料造价,未能关注整体结构优化的经济性指标。鉴于此,引入总造价PT作为评价经济性的指标,
PT=MsPms+VcPvc
(3)
式中,Pms是钢筋平均造价(¥/t),暂取¥3000/t;Pvc是混凝土平均造价(¥/m3),暂取¥500/m3;Ms是钢筋用量;Vc是混凝土体积用量。
单元的安全强度源于某载荷条件下内力组合加权,该内力组合加权可由计算配筋量反映,引入构件配筋率ρ来衡量结构的强度安全性,
(4)
考虑到材料用量与经济性的关系,式(3)可进一步变为,
(5)
式中,ρe可称为钢筋造价比,它实际上是考虑了经济因素的构件配筋率。
采用梯度搜索法对优化变量进行敏感性分析,得到对冷却塔结构性能影响较大的13个参数(见表7)。塔筒参数见图8。除优化变量外的其它塔筒参数见表8。

表7 优化变量Table 7 Variables for optimization

变量物理含义R1筒顶半径H1筒顶高度R2喉部半径H2喉部高度R3筒底半径H3筒底高度H直线段高度
约束条件为:由冷却塔工艺性能确定塔筒顶半径、高度,筒底/柱顶半径、高度,喉部高度、半径;为保证线段I、II、III整体保持下凹曲线和圆锥直线,须满足:
(6)
(7)
塔筒的几何尺寸应结合结构、施工等因素确定,根据水工规范,确定在优化时塔型几何尺寸取值范围满足表9。此外,塔筒整体弹性稳定安全系数和局部弹性稳定安全系数不小于5.0;所有构件满足设计配筋要求,包括构件承载能力验算、裂缝验算、配筋率校核等。

表9 双曲线型通风筒壳体几何尺寸Table 9 Hyperbolic tower shell size
2.2 两阶段混合优化算法
本文优化算法是响应面法与梯度搜索法的结合。响应面法的原理是通过有限次确定性计算结果结合回归分析,拟合一个显性闭合多项式函数(即功能函数,其作用在于确定某特定目标域内的最优目标响应及其位置)来近似表达目标响应量与控制变量的隐性函数关系。这样我们可以利用功能函数来确定最优目标响应及其位置。但每一次确定性计算的迭代位置都需要根据上一次计算位置的梯度来确定,而基于敏感性分析技术的梯度搜索法为计算具有复杂形式功能函数的梯度矢量提供了有效的手段。通过响应面法与梯度搜索法的结合,我们可以计算每一迭代位置的功能函数值及其梯度矢量,逐步逼近最优响应。
响应面法是一种结合统计方法的渐进拟合算法,它适用于目标响应量受多个控制变量影响的问题,其目的在于得到考虑控制变量随机性或不确定性之后的最优目标响应。
梯度搜索法是基于随机有限元法的敏感性分析技术而发展的优化算法,通过敏感性分析可以获得功能函数在当前计算位置的梯度矢量,进而确定下一步计算位置。随机有限元法是考虑了变量(如载荷、构件截面面积、惯矩、材料弹性模量等)的随机性或不确定性的有限元法,适用于解决具有较强随机性的复杂结构问题,这种方法在简单结构的随机场分析、材料及几何非线性分析等领域已经开始了初步尝试。其中,敏感性分析技术可了解基本变量的随机性对于结构不确定性的贡献程度,根据某变量对结构响应的影响程度,或收集更多的信息以改善结构设计的可靠性,或忽略某些变量以在不影响结果的情况下提高计算效率。
现利用响应面法与梯度搜索法解决“寻找特定区域内海拔最高点”这一问题,来说明响应面法与梯度搜索法的实现过程。问题:利用优化检验函数eggholder构造一个三维曲面函数z=g(x,y)来表示某区域的地形,见图9。其中,z为海拔高度,(x,y)为区域水平坐标,-1000≤x,y≤1000,zmax=2289.1。通过区域任一点坐标(x,y)可得其海拔z,利用响应面法、梯度搜索法寻找此区域海拔最高点及其海拔值。
优化实现步骤如下:
(1) 在区域内均匀选取计算点(x,y),见图10,得到相应的海拔z;
(2) 构造显性闭合多项式函数:
(7)
其中,i、j是整数,i+j=5。对第二步中的数据(x,y,z)采用最小二乘法进行回归分析,得到拟合曲面(图11a),最高海拔点有较高概率位于海拔在2000~2200 m的右上角区域(图11b);
(3) 选取鹅黄色区域内海拔较高点作为起始点,沿其某一较大梯度方向选取下一点,若下一点的海拔较高,则以下一点为新的起始点;若下一点海拔较低,改变方向重新选取下一点,直至确认当前点海拔最高,搜索终止。在此选取1个起始点(图12),即1号点(800,800),沿其较大梯度方向(黑色的点代表可以选取的点,各点最大梯度方向如红色箭头标记)选取2号点(700,800),以此类推,黑色虚线标记出了搜索路径,4号点是搜索到的海拔最高的点,其海拔为2220.4 m,为最高海拔的97%。
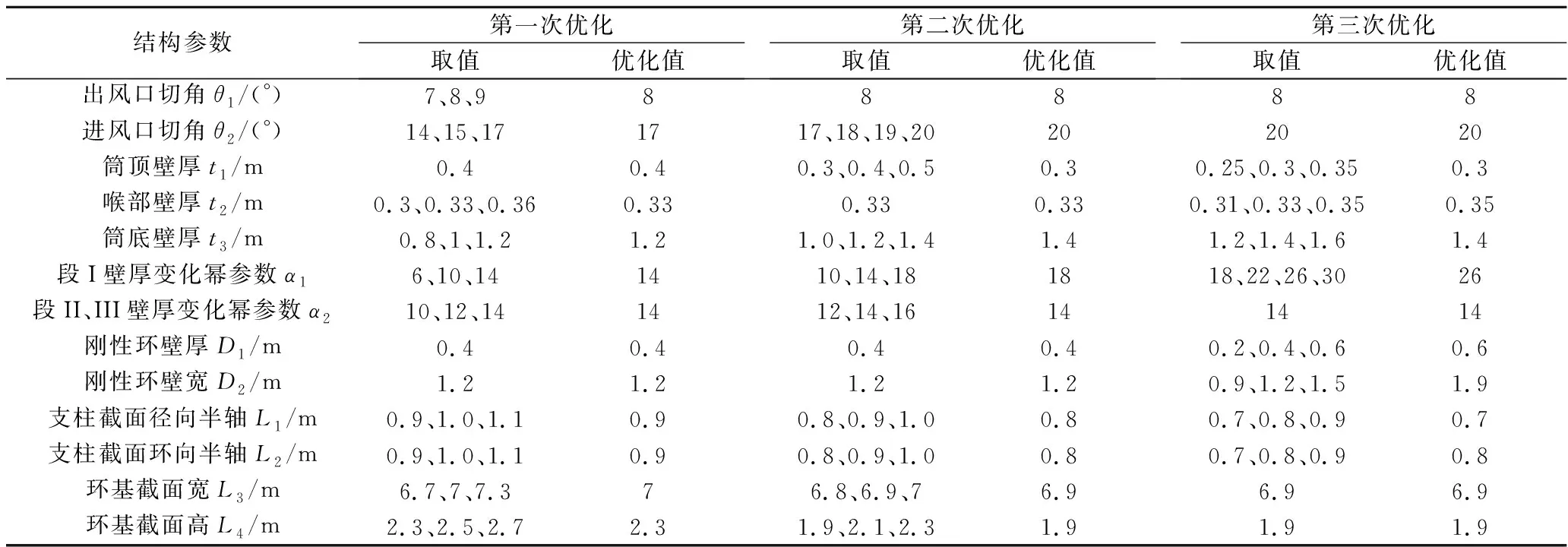
结构参数第一次优化取值优化值第二次优化取值优化值第三次优化取值优化值出风口切角θ1/(°)7、8、988888进风口切角θ2/(°)14、15、171717、18、19、20202020筒顶壁厚t1/m0.40.40.3、0.4、0.50.30.25、0.3、0.350.3喉部壁厚t2/m0.3、0.33、0.360.330.330.330.31、0.33、0.350.35筒底壁厚t3/m0.8、1、1.21.21.0、1.2、1.41.41.2、1.4、1.61.4段I壁厚变化幂参数α16、10、141410、14、181818、22、26、3026段II、III壁厚变化幂参数α210、12、141412、14、16141414刚性环壁厚D1/m0.40.40.40.40.2、0.4、0.60.6刚性环壁宽D2/m1.21.21.21.20.9、1.2、1.51.9支柱截面径向半轴L1/m0.9、1.0、1.10.90.8、0.9、1.00.80.7、0.8、0.90.7支柱截面环向半轴L2/m0.9、1.0、1.10.90.8、0.9、1.00.80.7、0.8、0.90.8环基截面宽L3/m6.7、7、7.376.8、6.9、76.96.96.9环基截面高L4/m2.3、2.5、2.72.31.9、2.1、2.31.91.91.9
2.3 优化过程和结果
载荷组合取水工规范规定的工况,基本风压取0.45 kPa。为实现较符合实际的内力载荷组合效应,分析过程计了地震烈度(本例取8°)、自重和温度载荷组合效应,但实际配筋过程最终均以风载荷为控制内力。以规范模式二维对称风压为例说明每次优化变量设置及相应的优化结果。
设置优化变量时,在中间值上下分别取值,如果优化值小于中间值,则降低取值下限;若等于中间值,则暂不优化或降低取值步长;若大于中间值,则提高取值上限。优化变量第一次优化的变量取值设置如下:θ1、θ2是子午线形状的决定性参数;t2对稳定性有较大影响,t3会约束t1、t2取值允许范围,参与第一次优化;L1、L2、L3、L4为下部结构(底支柱、环基)主要尺寸,参与第一次优化。第一次优化结果如下:θ1、t2取中间值,暂不优化;θ2、t3、α1、α2都达到取值上限,应提高取值上限;L1、L2、L3、L4达到取值下限,应降低下限;以此指导第二次优化变量设置。同样以第二次优化结果指导第三次优化变量设置。优化变量设置见表10。
经三次优化,所得推荐塔型的整体、局部稳定系数较初始塔型都有提高,且满足水工规范不小于5.0的要求,用钢量下降23.3%,用砼量下降12.2%,钢筋造价比下降5.4%,总造价下降19.0%,具体结果见表11。第一次优化组合总数59049,迭代次数约4000次,相比于控制变量法和穷举法,优化效率得到了极大的提高。
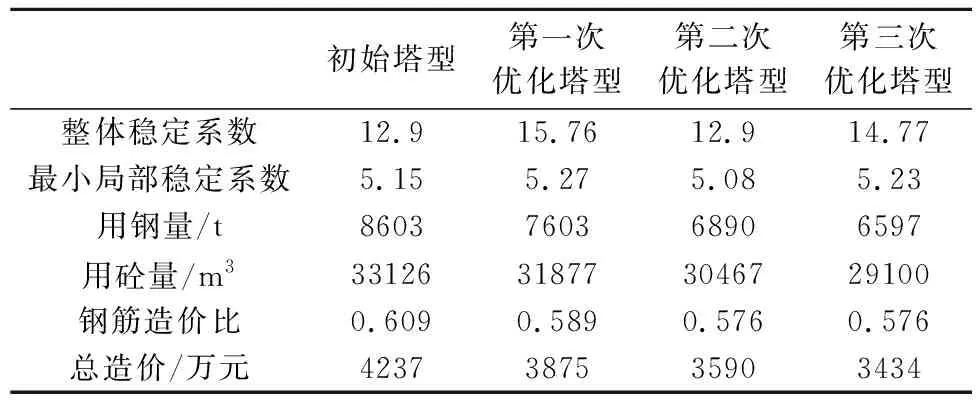
表11 优化结果Table 11 Optimization results
对于遮挡干扰三维非对称风压、试验等效三维非对称风压、通道加速气流三维对称风压均按照相同的方式优化三次得到推荐塔型,连同规范模式二维对称风压下的推荐塔型与初始塔型对比结果见表12,各推荐塔型的子午线型见图13。

表12 各推荐塔型通风筒结构参数Table 12 Structural parameters of optimized towers
相较于初始塔型,各推荐塔型:喉部以上子午线形与初始子午线形十分接近,对结构性能影响较小;喉部以下子午线形接近,但曲率均较初始子午线形增大,对结构性能影响显著。t3>t2>t1,t1接近0.25 m,t2分布在0.33 m~0.35 m,t3分布在1.2 m~1.4 m;α1最优值差异较大,这与较小的局部稳定系数分布的模板位置有关,对规范对称风压、试验侧向非对称风压而言,较小的α1意味着喉部以上壁厚减小,局部稳定性降低,可能小于5.0,不满足水工规范对于局部稳定性的要求;α2都分布在10~14,意味着喉部以下大部分子午向模板壁厚都等于t2;刚性环壁宽厚比D2/D1为1.5,支柱截面环向径向半轴比L2/L1分布在1.1~1.4,环基截面宽高比L3/L4分布在3~4。
为选定最优塔型,对各推荐塔型在4种风载荷分布模式下进行了关于塔筒稳定性、强度安全性和经济性的交叉对比,见表13、表14。限于篇幅,只给出了选定的最优塔型在各风载荷分布模式下的塔筒理论配筋曲线,见图14。

表13 各推荐塔型交叉对比稳定性验算Table 13 Cross check for stability of optimized towers
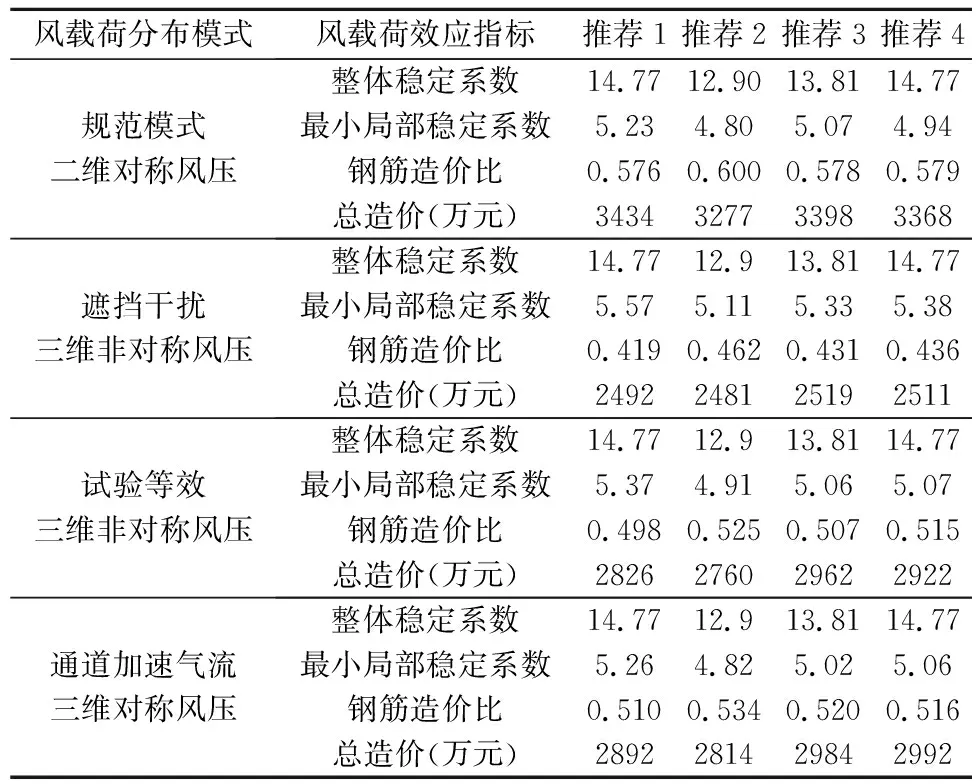
表14 各推荐塔型交叉对比Table 14 Cross checkof optimized towers
推荐塔型2在除了遮挡干扰三维非对称风压下最小局部稳定系数都小于5.0,推荐塔型4的最小局部稳定系数在规范模式二维对称风压下小于5.0,两者都不满足水工规范关于局部稳定性的要求。只有推荐塔型1、3通过了稳定性验算。在各风载荷分布模式下,推荐塔型1与推荐塔型3的各项指标都很接近,但推荐塔型1在除了规范模式二维对称风压下的经济性指标没有明显的优势外,其余载荷分布下稳定性、强度安全性、经济性都略胜一筹——整体稳定系数提高6.9%,局部稳定系数最大提高6.1%,钢筋造价比最大降低2.8%,总造价最大降低4.6%。可以认为推荐塔型1的子午线形和整体结构刚度分配更加合理,在规范二维模式对称风压和复杂群塔条件下,均能提高结构效率。
一种推荐塔型在其它风载荷分布模式下的稳定性、强度安全性、经济性指标难以呈现出相同结果。对比塔筒理论配筋,不难发现同一塔型在不同风载荷分布模式下的配筋截然不同:在规范对称风压下,推荐塔型1的子午向外侧、内侧理论配筋量在绝大多数塔筒范围内都大于其它风载荷分布模式的相应值;环向外侧、内侧至少70%的塔筒范围内配筋量都不小于其它风载荷分布模式的相应值;其余曲线交叉情况出现在0.9H及以上或0.12H及以下的塔筒,端部三维绕流效应明显,规范对称风压下的配筋趋于保守,在结构配筋设计中可采用图14中配筋包络曲线保证结构强度。总体来说,推荐塔型1在规范二维对称风压下的配筋较多,这也是推荐塔型1经济性略低于在其它三种风载荷下设计结果的原因。
从塔筒稳定性(整体、局部稳定系数)、强度安全性(钢筋造价比、塔筒理论配筋量)和经济性(总造价)三方面,可选取推荐塔型1作为六塔组合的最优塔型。在规范对称风压下,最优塔型的稳定系数相较于初始塔型的都有提高,钢筋造价比降低5.4%,总造价降低19.0%,见表15。

表15 规范对称风压下综合指标对比Table 15 Comprehensive indicators under standard symmetrical wind pressure
3 结 论
本文定义内力组合加权效应(配筋量)和总造价为综合效应指标,针对六塔组合,实施了冷却塔抗风设计的分阶段设计策略。主要结论有:
1) 典型试验风载荷模式呈现三维非对称分布的特征,沿高度分别拟合风压分布曲线能更准确指导结构设计。
2) 推荐塔型与初始塔型的主要差异在于塔筒下部的子午线形,对塔筒下部子午线形的优化能明显提升结构性能。
3) 推荐塔型受风载荷作用模式的控制,各塔型经多种风载荷作用模式的交叉验证推选综合性能最优塔型。
4) 最优塔型的配筋量依赖风载荷作用模式的选取,塔筒子午向配筋受影响最明显。多种配筋的外延包络能保证结构在复杂干扰条件下的设计安全。
参 考 文 献:
[1]Wu J K. Review and prospect of structural analysis of large-scale cooling towers[J]. Mechanics in Engineering, 1996, 18(6): 1-5. (in Chinese)武际可. 大型冷却塔结构分析的回顾与展望[J]. 力学与实践, 1996, 18(6):1-5.
[2]GB50102T-2014. 工业循环水冷却设计规范[S].
[3]DL/T5339-2006. 火力发电厂水工设计规范[S].
[4]Liu M H. Optimized calculation and model slection of double curved cooling towers[J]. Electric Power Construction, 2000(10): 35-38. (in Chinese)刘明华. 双曲线冷却塔结构优化计算与选型[J]. 电力建设, 2000, 21(10): 35-38.
[5]Cong P J, Sheng L I, Chen D, et al. Study of optimization of indirect dry cooling tower structure[J]. Engineering Journal of Wuhan University, 2011(s1):330-333. (in Chinese)丛培江. 间接空冷塔结构优化研究[J]. 武汉大学学报(工学版), 2011(s1): 330-333.
[6]Li W, Chai J, Zheng J. Investigation of natural draft cooling tower in China[J]. Heat Transfer Engineering, 2016, 38(11-12): 1101-1107.
[7]Davenport A G. Gust loadingfactors[J]. Journal of the Structural Division, 1967.
[8]Kasperski M. Extreme wind load distributions for linear and nonlinear design[J]. Engineering Structures, 1992, 14(1):27-34.
[9]柯世堂. 大型冷却塔结构风效应和等效风载荷研究[D]. 上海: 同济大学, 2011.
[10]Zhao L. Aerodynamic and aero-elastic performances of super-large coolingtowers[J]. Wind and Structures, 2014, 19(4): 443-465.
[11]Zhao L, Chen X, Ge Y. Investigations of adverse wind loads on a large cooling tower for the six-towercombination[J]. Applied Thermal Engineering, 2016, 105: 988-999.
[12]Csonka P. Hyperbolic shaped cooling tower with a mantle-wall of equal strength[J]. Acta Techn. Hung, 1963, 44: 96.
[13]Konstruktiver Ingenieurbau—Berichte. Ruhruniversitüt Bochum Heft1 bis 7.
[14]Coll. On recommendations for thestruct. design of hyperbolic or other similary shaped cooling towers[C]//Brüssel: IASS, 1971.
[15]Greiner-Mai D, Auerbach W. Beitrag zur Entscheidungsfindung beim Entwurf hyperbolischer Kühltürme mit besonderer Breücksichtigung des statisch-konstruktiven Aspekts[M]. Dissertation, IIAB Weimar, 1973.
[16]Lagaros N D, Papadopoulos V. Optimum design of shell structures with random geometric, material and thickness imperfections[J]. International Journal of Solids & Structures, 2006, 43(22-23): 6948-6964.
[17]Uysal H, Gul R, Uzman U. Optimum shape design of shell structures[J]. Engineering Structures, 2007, 29(1): 80-87.
[18]张宗方. 大型自然通风冷却塔失效分析与优化设计[D]. 大连: 大连理工大学, 2011.
[19]Rumpf M, Grohmann M, Eisenbach P, et al. Structural surface-multi parameter structural optimization of a thin high performance concrete object[C]//International Association for Shell and Spatial Structures, 2015.
[20]Wu Y, Xia Y, Li Q. Structural morphogenesis of free-form shells by adjusting the shape and thickness[C]//International Association for Shell and Spatial Structures, 2015.
[21]Mungan I. Buckling stress states of cylindrical shells[J]. Journal of the Structural Division, ASCE, 1974, 100(11): 2289-2306.
[22]Mungan I. Buckling stress states of hyperboloidal shells[J]. Journal of the Structural Division, ASCE, 1976, 102(10): 2005-2020.
[23]Mungan I. Buckling stress of stiffened hyperboloidal shells[J]. Journal of the Structural Division, ASCE, 1979, 105(8): 1589-1604.
[24]Mungan I. Buckling of stiffened hyperboloidal cooling towers[J]. Journal of the Structural Division, ASCE, 1979, 105(10): 1999-2007.
[25]Almannai A, Basar Y, Mungan I. Basic aspects of buckling of cooling tower shells[J]. Journal of the Structural Division, ASCE, 1981, 107(3): 521-534.
[26]Zerna W, Mungan I. Wind-buckling approach for RC cooling towers[J]. Journal of the Engineering Mechanics, 1983, 109(3): 836-848.
[27]Zhan Y Y, Zhao L, Liang Y W, et al. comprehensive assessment of wind-induced interference criteria about large cooling towers with typical six-towers double-columns arrangements[J]. Engineering Mechanics, 2017, 34(11): 66-76. (in Chinese)展艳艳, 赵林, 梁誉文,等. 大型冷却塔群塔组合(六塔双列)风致干扰准则综合评价[J]. 工程力学, 2017, 34(11): 66-76.
[28]Zhao L, Zhan Y Y, Ge Y J. Wind-induced equivalent static interference criteria and its effects on cooling towers with complex arrangements[J]. Engineering Structures, 2018, 172: 141-153.

