沥青路面加热过程中温度分布的随机性研究
顾海荣,梁奉典,李金平,董强柱,徐信芯
(长安大学 公路养护装备国家工程实验室,陕西 西安 710064)
0 引 言
沥青路面就地热再生工艺中,首先利用加热机对需要再生的旧沥青路面进行加热,待沥青路面4 cm深处的温度达到100 ℃以上时,通过耙松或铣刨、再生搅拌后摊铺压实,从而形成新的沥青路面。就地热再生过程中,加热装置的加热功率很难保持在某一个定值,存在或大或小的分散性,而沥青路面材料的不均匀,也会导致沥青路面的导热系数、比热容以及密度等参数具有随机特征。这些随机因素对就地热再生加热过程中沥青路面的温度分布具有重要影响。
随机温度场研究已受到国内外研究者的重视,如Madera A G和Karniadakis G E等对稳态随机温度场进行了分析,给出了可计算随机稳态温度场响应均值和方差的解析表达式[1-2];Emery A F对瞬态随机温度场提出一种多项式混沌算法[3];祁长青等研究了青藏铁路在环境温度和冻土的热学参数具有随机性时的温度场[4];刘宁等提出了大体积混凝土结构温度场的随机有限元算法[5];王小兵等研究随机温度场Monte-Carlo模拟法的一类近似处理的方法[6]。上述工作从不同角度研究了随机温度场问题,但是对沥青路面就地热再生加热过程中温度场随机性的研究甚少。大多数学者在研究沥青路面就地热再生温度场时,都将各物理参数视为确定性的单值变量,忽略了各种导致这些变量产生随机性的因素。
本文结合Monte-Carlo随机有限元法和MATLAB软件,研究就地热再生过程中的加热热流密度、沥青路面材料的导热系数、比热容以及密度等参数的随机性对沥青路面温度场的影响,获得沥青路面就地热再生过程中温度场的统计特性。
1 沥青路面瞬态传热方程

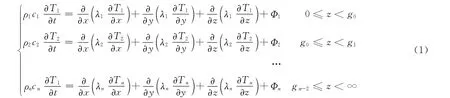

图1 截面
式中:T为沥青混合料温度(℃);t为时间(s);Φ为微元体内热源的生成热(W·m-3);λ为沥青路面的热传导系数(W·(m·K)-1);ρ为沥青混合料的容重(kg·m-3);c为沥青混合料的比热容(J·(kg·K)-1)。


式中:qx为与传输方向相垂直的单位面积上的传热速率,即通过x方向的热流密度。
类似的表达式也可用于与y、z方向上相垂直的热流密度。
由式(1)和式(2)分析可知,影响沥青路面加热过程中传热的因素主要有沥青路面的厚度hi和深度gi、导热系数λi、密度容重ρi和比热容ci以及沥青路面表面的热流密度q等。
本文主要分析热流密度q、沥青路面的导热系数λi、比热容ci以及密度ρi的随机性对沥青路面温度场随机性的影响。
2 沥青就地热再生温度场的随机性研究
沥青路面加热过程中的各参数为随机参数,需采用随机有限元法进行分析。考虑到随机变量较多,若用纯数学的方法很难推导出节点温度变化的表达式。故本文采用Monte-Carlo法进行随机模拟[8]。
根据模型尺寸及相关参数建立沥青路面的三维有限元模型(将沥青路面视为一个均质体,路面结构各层组成材料均匀、连续且各向同性)。加热装置在路表面进行加热,由于持续加热时间有限,路面内部温度传递速度较慢,热量还来不及传递到下面层、基层、底基层和路基层。因此,本文建立的沥青路面三维模型模拟深度仅到中面层,模型尺寸为0.01 m×0.01 m×0.10 m[9-10]。利用8节点六面体的实体单元Thermal solid70进行网格划分。水平方向上网格尺寸设为0.002 m。深度方向上沿路面结构自上而下进行划分,上面层网格尺寸设为0.002 5 m,划分为16层;中面层网格尺寸设为0.003 75 m,划分为16层,如图2所示。

图2 沥青路面有限元模型
针对各种沥青混合料的热物性参数方面的研究,国内外研究学者做了大量的工作,也得出了很多有价值的数据,现将研究所得的数据结果进行整理,如表1所示。

表1 国内外沥青混合料热物参数范围值
在沥青路面加热过程中,一般要求将4 cm深处的温度加热到100 ℃以上。因此,本文只需考虑沥青路面上面层各热学参数的随机性,利用密度公式ρ=M/V,式中:M为混合料的质量;V为混合料的体积。进行多次测量并计算出某一沥青混合料的密度,根据热平衡原理测出这一沥青混合料的比热容,同时采用防护热板法进行其导热系数的测量。并将这些热学参数作为基本随机变量[11]。各随机参数的均值如表2所示。

表2 随机变量均值
将沥青路面表面温度记为T0、沥青路面深度0.5cm处温度记为T0.5、以此类推间隔0.5cm分别记为T1、T1.5、T2、T2.5、T3、T3.5和T4。提取上述各深度的温度曲线,并储存。
将建模分析命令生成一个完整的命令流文件,作为ANSYS中概率设计模块PDS的输入文件。选择Monte-Carlo拉丁超立方法作为概率设计方法。模拟次数设为5 000次,随机变量q、λ、c、ρ的变异系数[12-13](均方差与均值之比)分别为vq、vλ、vc和vρ。
为了检验设定的模拟次数是否足够,图3给出了多次模拟后路面表面加热130 s时温度的均值收敛曲线。由图3可以看出,目标变量温度的均值收敛曲线在模拟2 000次后趋于稳定,表明模拟次数足够,所求出的温度准确。

图3 目标变量温度的均值收敛曲线
模拟完成后就可对不同时刻沥青路面结构的温度场进行统计分析。图4为各随机变量的变异系数均为0.03(即vq=v=vc=vρ=0.03)时路面表面温度场的概率密度分布图。

图4 概率密度分布
由图4可知,沥青路面表面温度在不同时刻的温度概率密度分布总体上符合正态分布。为了进一步验证其概率密度分布类型,将ANSYS中计算出来的表面温度加热130 s的结果导入MATLAB软件中进行概率密度函数分析,经拟合后呈现出明显的正态分布,如图5所示。

图5 130 s时表面的温度分布概率密度
利用MATLAB软件可获得T0~T4在110、130、150 s(130 s为加热到目标均值在180 ℃,即达到就地热再生施工表面最高允许温度的情况)的均值和变异系数。为了便于比较,表3给出了T0~T4温度分布在各个时刻的均值和变异系数。结合图5和表3,若按3σ原则可知表面温度加热130 s时所在区间为[μ-3σ,μ+3σ],即[165 ℃,202 ℃],可见参数变异性对温度分布变异性的影响非常明显,考虑参数变异性后,加热后的路面各点温度服从统计规律,不再是单一值,这更符合实际施工情况。
为了考察各参数的随机性对沥青路面热再生温度场分布的影响,在随机模型中分别考虑了热流密度q、沥青路面导热系数λ、沥青路面比热容c以及沥青路面密度ρ其中之一为随机变量和四者同时为随机变量的情况。
图6绘制出了加热130 s时各参数的变异性对温度分布随深度变化的趋势图。

图6 加热130 s时各参数的离散性对温度分布随深度变化的趋势
图6、7分别绘制出了加热130 s时各参数的离散性和变异性对温度分布随时间变化的趋势。由图6可知,vc和vρ对温度响应影响的趋势图几乎重合,这表明vc和vρ对温度响应的影响是几乎一样的。
由表3、图6和图7可知以下几点。
(1)当各参数的分散性增大时,温度分布的分散性呈现出增大的趋势。同时考虑热传导中各参数的随机性,温度分布的分散程度要大于只考虑单个参数的分散性时的分散程度。随着时间推移,节点温度的分散性也增加。
(2)热流密度q的分散性对沥青路面表面温度分散程度的影响是最大的,且随着深度的增加,其分散性对温度分布分散程度的影响迅速减小。因此在施工时应该要精确控制热流输入,减小其波动性。在沥青路面上面层内部,比热容c和密度ρ的分散性对温度分布分散程度的影响最大,且二者的影响几乎相当。

表3 沥青路面不同时刻不同深度处节点温度的均值和变异系数
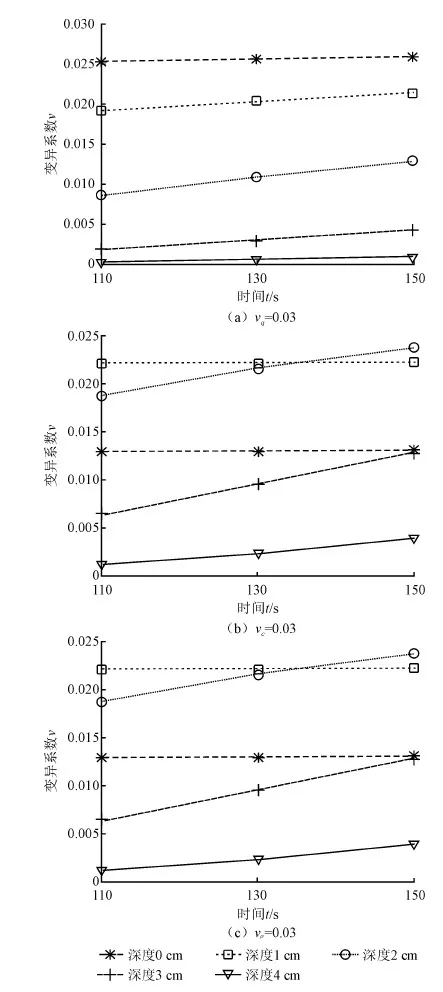
图7 加热130 s时各参数的变异性对温度随时间变化趋势的影响
(3)对于沥青路面上面层,导热系数λ的分散性对温度分布分散程度的影响先减小后增大然后再减小;比热容c和密度ρ的分散性对温度分布分散程度影响先增大后减小。
(4)单独考虑每个参数的分散性对温度分布分散性的影响时,热流密度q、比热容c和密度ρ的分散性对沥青上面层温度分散性的影响随加热时间的增加而增大。
(5)本文所建模型虽没有考虑就地热再生机组运行速度的差异对温度分布分散性的影响,但在加热相同长度的沥青路面时,行驶速度越快,则加热时间越短;行驶速度越慢,则加热时间越长。故加热机组速度差异的影响可通过不同时刻温度的变异性大小来体现,正如本文加热到110 s、130 s和150 s的情况。
3 结 语
本文利用Monte-Carlo随机有限元法和MATLAB软件,研究了沥青路面就地热再生加热过程中温度分布的随机性。该法可利用温度变化的变异系数或均方差来衡量实际施工中随机因素对加热温度分布的影响,并分析了各随机因素对温度分布的影响,得出以下结论。
(1)考虑热传导中各参数的随机性时,温度分布的分散程度大于只考虑单个参数的分散性时的分散程度,且随着各参数分散性的增大,温度分布的分散性亦呈现出增大的趋势。随着时间推移,节点温度变化的分散性也增加。
(2)导热系数λ、密度ρ、热容c以及热流密度q的分散性对温度分布分散性的影响是有差异的,同一时刻热流密度q的分散性对沥青路面表面温度分布分散性的影响是最大的,且随着深度的增加其影响迅速降低;在沥青路面上面层内部,比热容c和密度ρ的分散性对温度分布的分散程度影响占主要地位,且二者的影响几乎相当。
(3)基于热学参数分析结论可知,热学参数的随机性会导致温度分布的随机性,因此要求在热再生时应尽可能减小各参数的随机性,如提高加热机加热系统的控制精度,将加热功率即热流密度严格的控制在某一恒值上。
参考文献:
[1] MADERA A G,SOTNIKOV A N.Method for Analyzing Stochastic Heat Transfer in a Fluid Flow [J].Applied Mathematical Modelling,1996,20(8):588-592.
[2] KARNIADAKIS G E,XIU D B.A New Stochastic Approach to Transient Heat Conduction Modeling With Uncertainty [J].International Journal of Heat and Mass Transfer,2003,46(24):4681-4693.
[3] EMERY A F.Some Thoughts on Solving the Radiative Transfer Equation in Stochastic Media Using Polynomial Chaos and Wick Products As Applied to Radiative Equili-Brium [J].Journal of Quantitative Spectroscopy and Radiative Transfer,1997,123(12):1219-1229.
[4] 祁长青,吴青柏,施 斌,等.青藏铁路冻土路基温度场随机有限元分析 [J].工程地质学报,2005,13(3):330-335.
[5] 刘 宁,刘光延.大体积混凝土结构温度场的随机有限元算法 [J].清华大学学报:自然科学版,1996,36(1):41-47.
[6] 王小兵,陈建军,梁震涛,等.随机温度场Monte-Carlo法的一类近似处理 [J].系统仿真学报,2007,19(10):2156-2160.
[7] 董强柱,顾海荣,张 珲,等.就地热再生过程中的沥青路面加热功率控制[J].中国公路学报,2016,29(4):153-158.
[8] 张德育,黄晓明,马 涛,等.沥青路面就地热再生加热温度场模拟分析[J].东南大学学报:自然科学版,2010,40(6):1282-1287.
[9] 冯德成,胡伟超,于 飞,等.沥青路面材料热物性参数对温度场的影响及敏感性分析[J].公路交通科技,2001,11(28):12-19.
[10] 冯德成,李兴海,郭大进,等.基于热物理特性的沥青混合料的研究[J].公路交通科技,2010,27(3):28-33.
[11] DINA KUVANDYKOVA.A Model for Predicting Thermal Properties of Asphalt Mixtures From Their Constituents [D].Russia:Ufa State Petroleum Technological University,2007.
[12] 李金平.不确定性温度场和结构的分析方法研究 [D].西安:西安电子科技大学,2009.
[13] 李兴海.沥青混合料的热物特性研究 [D].哈尔滨:哈尔滨工业大学,2007.

