一种基于融合算法的管道泄漏信号处理方法

李传宪, 石亚男, 姬中元, 张雪立, 朱浩然, 逯雯雯

(1.中国石油大学 储运与建筑工程学院, 山东 青岛 266580; 2.中国石油化工股份有限公司 胜利油田分公司东辛采油厂, 山东 东营 257061)

在输油管道泄漏检测中，受噪声信号的干扰，工况误报和漏报现象时有发生，因此需要对传感器采集到的压力信号进行去噪处理，提高工况识别精度。小波去噪是一种自适应的时域和频域同时局部化的多分辨率分析方法[1]，因而在工业实际中得到广泛应用，然而，受时频联合分析原理所限，当噪声信号较多时，噪声信号与有用信号重叠较多，信号重构难度大[2]，消噪效果不明显，再加上泄漏信号的不断衰减，管道微小泄漏不易被发现[3]。因此，对长输管道泄漏信号的去噪处理至关重要，这是降低泄漏误报率和漏报率的关键，在管道安全运行领域有着迫切的工程需要。

针对上述问题，本文先利用自行改进的环道装置模拟泄漏工况，运用小波去噪对采集到的压力信号进行处理，通过时频联合分析泄漏信号的衰减过程，从噪声干扰和能量衰减两方面阐释小泄漏不易被发现的原因；为改进去噪效果，建立了新阈值函数提高重构精度，并从数学角度分析了它的优越性，将改进的新阈值去噪方法与盲源分离技术相融合，在泄漏信号中添加三组已知的噪声信号，通过分离已知构造信号说明此方法实际效果。

1 管输实验

根据实验室现有条件自行设计的环道装置总长370 m，内径25 mm，主要由管道系统、测量系统、电控系统及数据采集处理系统等组成(见图1)，包括空气循环流程、液体循环流程和数据采集流程等。

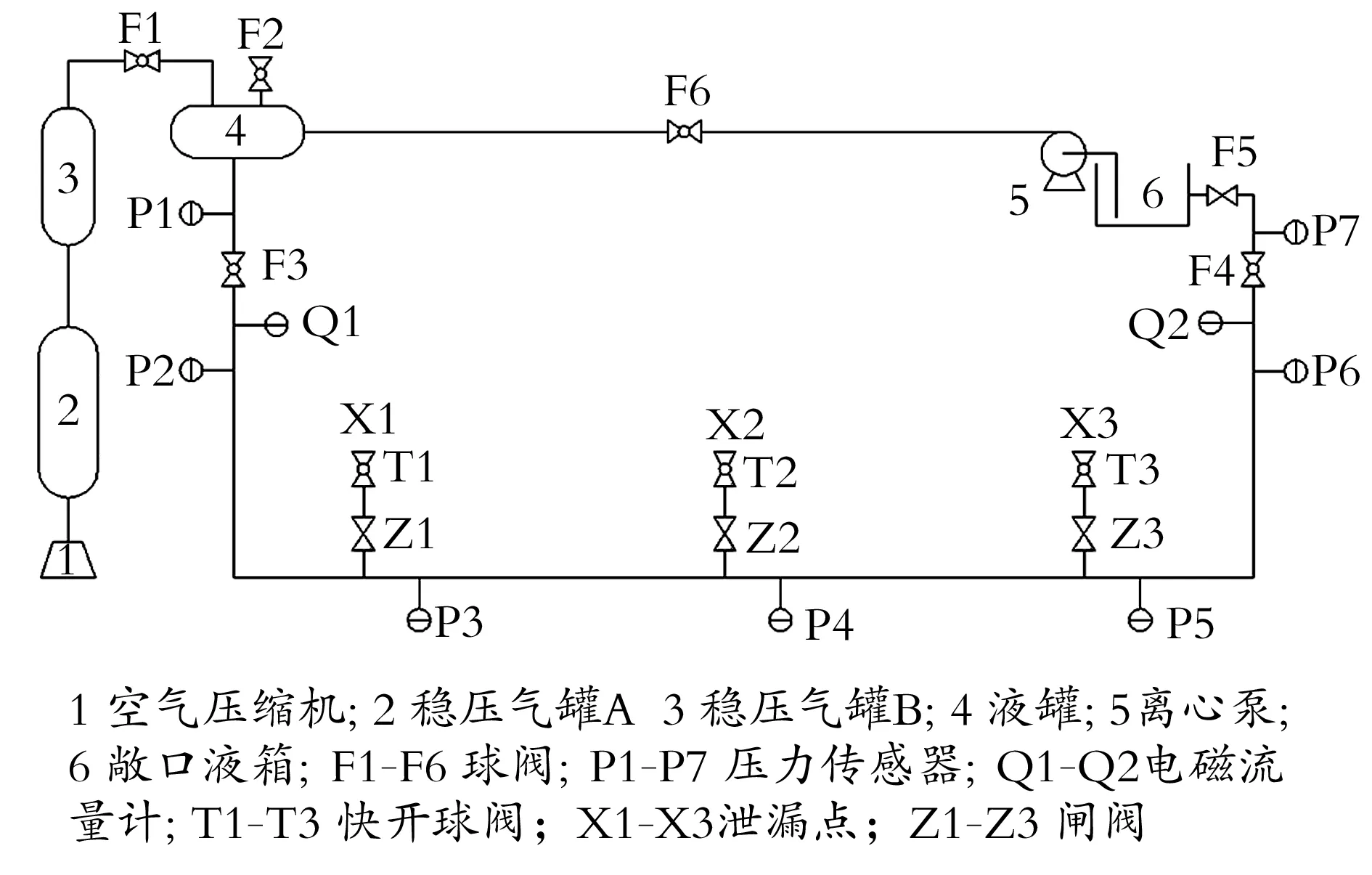
图1 小型环道实验装置

Fig.1Schematicdiagramofsmallloopexperimentalapparatus

空气循环流程：空压机压缩空气至稳压气罐A，以缓冲其出口产生的压力脉动，并通过配备在稳压气罐B上的自力式调节阀进一步控制液罐上方气体空间的压力。

液体循环流程：液体在重力和气体压力的作用下沿管道流动，直至流入敞口液箱，实现对管道长输的模拟。敞口液箱中的液体通过离心泵加压后泵入液罐中，实现液体的循环利用。

数据采集流程：压力传感器和电磁流量计采集到的压力，流量信号通过专用的信号处理电路处理成电压信号后被数据采集卡采集，记录并存储于上位计算机中。

该装置实现了环道的小型化，体积小，占地面积少，所需实验液体少且投资维护成本相对较低，采用压缩机与稳压气罐相结合的方式代替离心泵，为管内流体提供动力，克服了长距离、小口径室内环道沿程摩阻损失大带来的一系列问题。此装置除可用于常规管输实验外，还可用于研究含气率对管输参数的影响、测量压力波速及其影响因素、评价最小可检测泄漏量等。

为对管道的泄漏工况进行实验，在沿线布置了X1、X2、X3三个泄漏点，它们与管道首端的距离分别为90.5、168.8、247.9 m。这三个泄漏点均由闸阀和球阀组成，安装效果如图2所示。与主管道直接相连的闸阀用于控制泄漏孔径的大小，通过调节闸阀的开度可以对泄漏孔径的大小进行调整，通过开启或关闭上方的球阀可以模拟泄漏是否发生，球阀动作的快慢可以用于模拟不同种类泄漏形成时间的不同。

图2 模拟泄漏结构的原理示意及安装效果

Fig.2Schematicandinstallationeffectdiagramofthesimulationleakagestructure

图3为传感器采集到的负压波信号，由于传感器安装在管道末端，泄漏引起的负压波在管道内已经经过了一段距离的传播。当泄漏发生时，压力信号由原来的平稳波动变为急剧下降，波形下降段包含了泄漏工况的发生时刻这一信息，这里隐含着泄漏工况判断的关键特征，但是随着负压波信号在传播过程中的不断衰减，压力信号的下降幅值逐渐减小[4]，同时，外部环境的干扰，再加上阀门等结构引起的流动噪声，使管道泄漏工况的关键特征被掩盖，极易造成工况误报和漏报[5]。因此，在实际应用中，需要对传感器采集到的信号进行消噪处理，以提高工况判断的准确性。

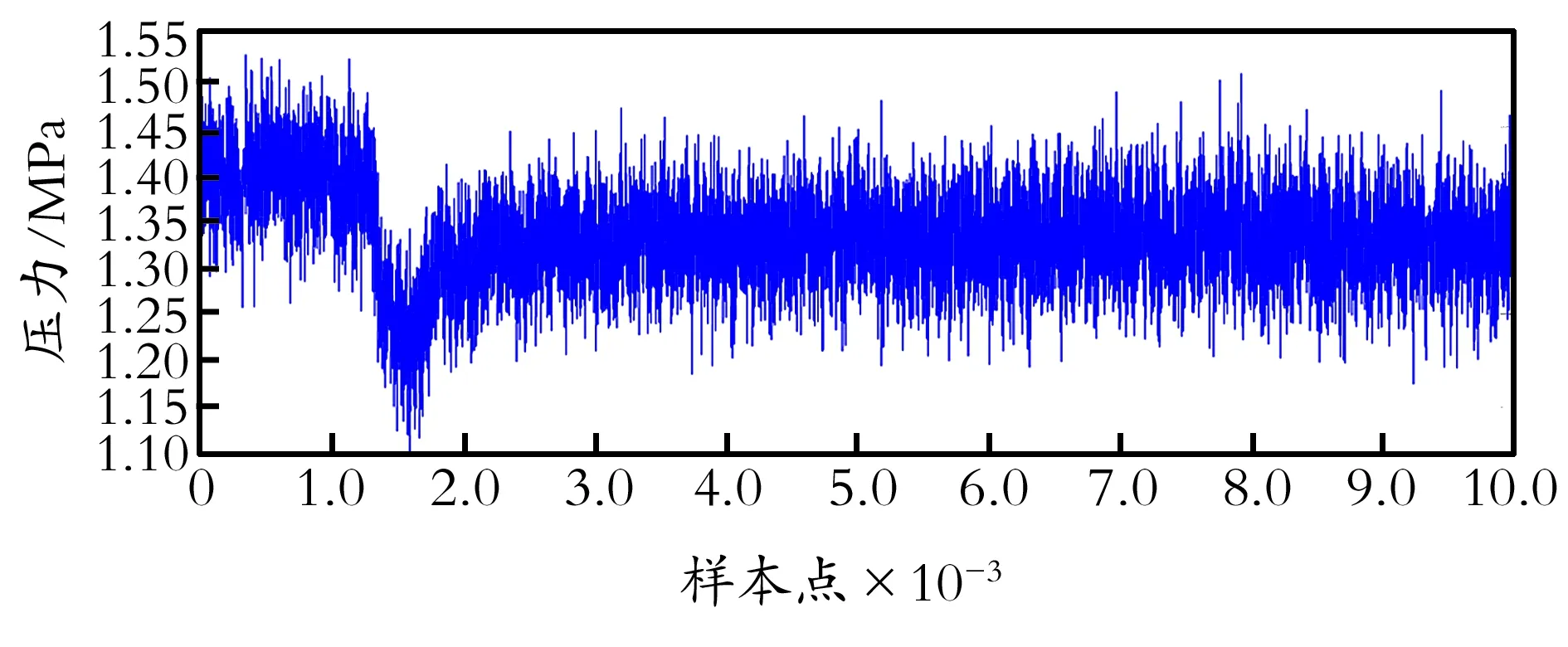
图3 传感器接收的波形信号

Fig.3Thewavesignalreceivedbythesensor

2 小波去噪

常用的时频消噪方法有很多，有维纳滤波、傅里叶变换消噪等，它们分别在时域和频域内对信号进行处理，滤除噪声信号[6]。由于小波变换能同时在时域和频域内对信号进行分析，所以它能将有用信号和噪声信号区分开来，从而实现信号的去噪处理[7]。

在工程实际中，有用信号一般表现为平稳的低频信号，噪声信号为高频信号，信号可以由小波分解后的小波系数来描述，小波系数越大，其携带能量越多。小波去噪的基本思想[8-9]就是根据噪声与有用信号在各尺度上的小波系数具有不同表现这一特点，将各尺度上由噪声产生的小波分量滤除，尤其是那些噪声分量占主导地位尺度上的噪声分量，然后将保留下来的小波系数利用小波算法，重构出原始信号中的有用信号。所以，本文以小波变换的信号处理方法对压力传感器采集到的信号进行滤波消噪，研究此方法的实际消噪效果。

利用小型环道实验装置进行实验，采样频率设为1 000 Hz，每组设置10 000个采样点，以尽可能保留泄漏产生的压力信号的时频信息。采集到的原始信号及处理后的信号如图4所示。

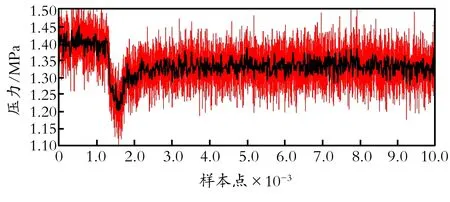
图4 传感器接收到的压力信号(红)和小波处理后的信号(黑)

Fig.4Thewavesignalreceivedbythesensor(red)andthesignalafterwaveletde-noising(black)

对去噪后的负压波信号进行处理，得到信号的时频谱图，如图5所示。

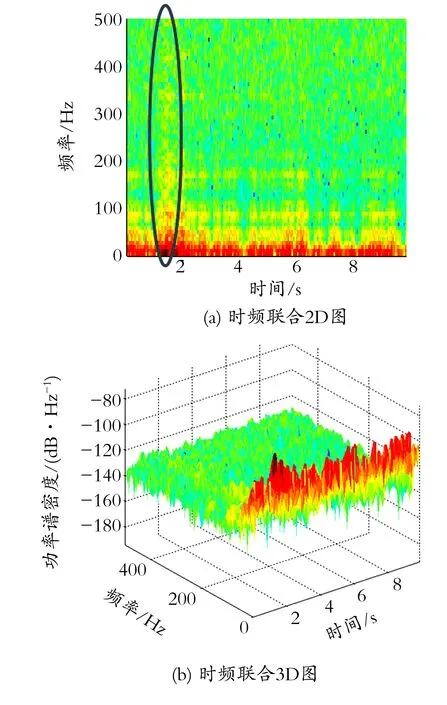
图5 时频联合分析图

Fig.5Time-frequencyanalysisofwavesignal2Dand3D

由时频联合分析可知，压力信号的能量主要集中在较低的频率范围，尤其是0～20 Hz信号的能量占主要优势，由于噪声的干扰，真实信号的频率存在波动。管道发生泄漏的瞬间(采集时间的1.7 s左右)，存在能量突变，随着泄漏逐渐稳定，能量随之衰减，高频段基本衰减完全，只有低频段还有部分能量，到6.3 s左右低频能量也衰减完全，达到一个新的稳定状态。

在实际工程中，长输管线沿途地形复杂，环境噪声比实验室大得多，管道结构复杂，同时又存在泵的启停、调阀、分输等操作，对信号干扰较大[10]。这些噪声信号的频率分布较宽，基本不会随着传播距离的延长产生衰减，容易被接收，对有用信号造成较大干扰。因此，由于噪声干扰和能量衰减等因素，小泄漏工况不易被发现，虽然小波去噪等时频去噪方法具有一定的去噪效果，受原理所限[11]，在工程实际中不能完全满足现场要求，需要新的方法弥补这一不足。

3 小波盲分离信号处理

盲源分离技术基于源信号的统计独立性，将几个无法直接观测的原始信号从观测信号中提取出来，实现信号的分离去噪，它的原理与时频消噪不同，从而为信号的消噪处理提供了一个新的思路，由于该方法中源信号和各信号的混合过程都是未知的，所以需要预先知道的信息少，具有较强的适应性[12]，图6为盲源分离的模型图。

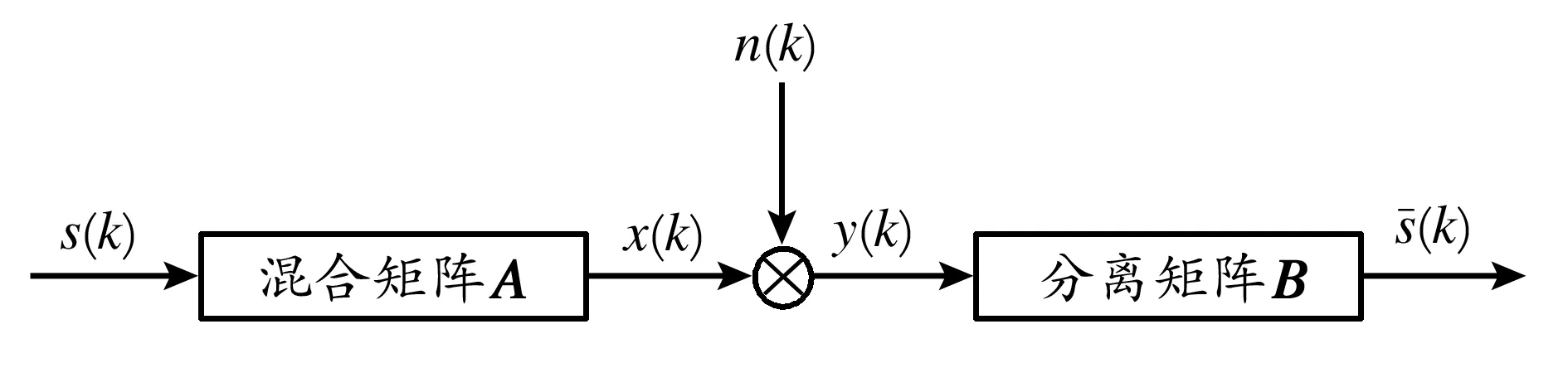
图6 盲源分离模型

Fig.6Blindsourceseparationmodel

在线性有噪混叠假设的前提下，采集到的压力信号被认为夹杂着一定程度的噪声污染。此时的盲源分离模型为线性瞬时混叠模型，其表达式为:

y(k)=As(k)+n(k)(1)

y(k),含噪随机观测信号向量；s(k)，源信号向量(各分量在统计上相互独立)；n(k)，噪声信号向量；A，混合向量。

找到一个常数分离矩阵，使估计源信号满足：向量中各分量之间的独立性最大。经过公式反推，可以得到源信号的最优估计为：

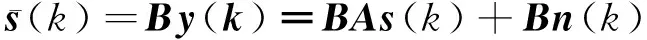
(2)

式(2)反推的分离方法只有在理想模型(不含噪声)下才能得到最优效果，当采集信号含有噪声时其效果会事倍功半[12]。因此，需要对采集信号进行处理。首先用改进后的小波消噪方法对信号进行预处理，以达到较好的分离效果。

3.1 预处理—改进的小波阈值去噪

小波去噪在工程应用中需要解决两个问题[13-14]：第一，如何选择合理的分解层数对信号进行分解；第二，按照什么样的原则进行阈值的选取。这两个问题对信号处理的优越性和可靠性起着至关重要的作用。信号的处理受分解层数的影响很大，如果分解层数选择过多，或对所有的各层小波空间的系数都进行阈值处理，将会使有用信号严重丢失，消噪后的信号信噪比反而有所下降，同时也会引起运算量增大，处理速度缓慢等问题；如果分解层数过少，则消噪效果不理想。与分解层数的选择相比，阈值的选择比较宽松，通常在一定范围内变动并不会导致消噪效果发生较大幅度的变化，因此需要一个能产生有效门限阈值的准则[15]。

在现有阈值去噪法的基础上做出一定的改进[13]，使用加权平均法，将硬、软阈值函数用加权平均的方法结合起来。设加权因子为μ，构造出式(3)的阈值函数：

(4)

从数学角度对新阈值函数进行分析：

(1) 新阈值函数的连续性

1) 讨论新阈值函数在λ处的连续性

所以，新阈值函数在λ处连续。

2) 讨论新阈值函数在-λ处的连续性

所以，新阈值函数在-λ处连续。

综上所述，新阈值函数在±λ处连续。

(2) 新阈值函数的渐近性

当wj,k→-∝时，

当wj,k→+∝时，

(3) 新阈值函数的偏差性

(4) 新阈值函数的高阶可导性

当|wj,k|≥λ时，新阈值函数满足高阶可导，从而便于各种数学处理。

与传统的硬、软阈值方法相比，新阈值函数提高了重构精度，减小了恒定误差，改善了去噪效果，具有明显的优势。

为了说明新阈值函数的改进作用，分别采用传统的硬、软阈值和新阈值函数进行去噪实验。本文选用matlab中自带源信号进行实验，结果见图7。

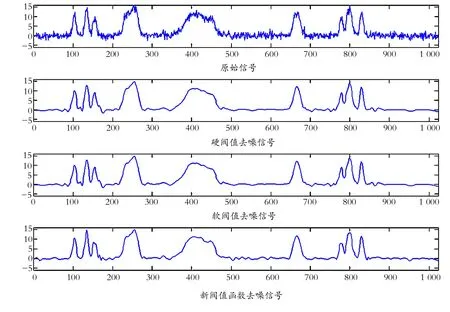
图7 不同阈值去噪效果对比

Fig.7Comparisonofde-noisingeffectswithdifferentthresholds

对比图7中4幅图，新阈值函数去噪法相对于软、硬阈值方法，信号逼近程度高且有效地抑制了吉布斯现象，处理后的信号存真率较高，有效抑制了有用信号的损失。为了定量评价三者去噪效果的优劣，可以计算去噪后信号的信噪比和均方根误差[13]，结果见表1。

设原始信号和去噪后的信号分别为x(n)、x′(n)，则信噪比可定义为：

(5)

则均方根误差定义为:

(6)

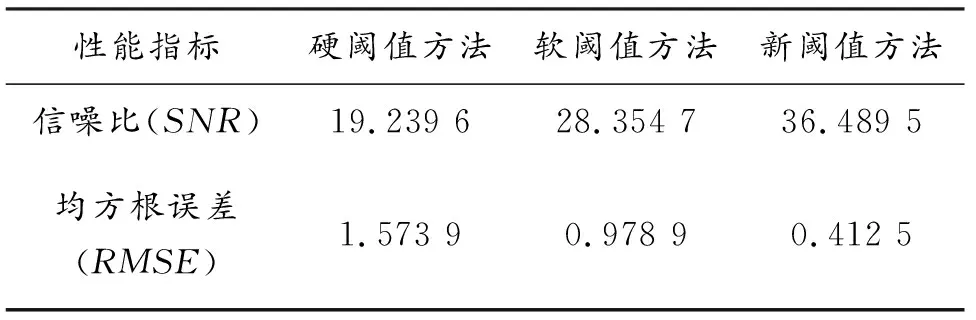
表1 三种方法的性能评价Table 1 Performance evaluation of three methods

信号的信噪比越高，原始信号和去噪信号的均方根误差越小，去噪信号就越接近原始信号，去噪的效果也就越好。由表1可直观看出，新阈值方法的去噪效果优于另外两种方法。

3.2 基于最大信噪比的盲源分离算法

基于最大信噪比的盲源分离算法是一种全局最优算法，此算法的依据是信噪比越大分离效果越好，进而将信噪比函数作为目标函数，通过机器自学习的方法确定分离矩阵[16]。

设s为源信号，x为混合信号，y为恢复信号，W为分离矩阵，则噪声信号可表示为e=s-y，则信噪比函数为：

(7)

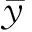
(8)

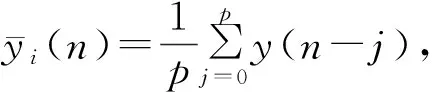
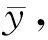
(9)

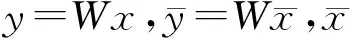
(10)

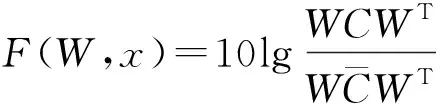
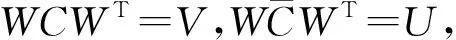
因为信噪比目标函数的极值点就是F(W,x)的零点，所以，

(11)

通过式(11)求解即可得到分离矩阵[16]。

当输油管道发生泄漏时，泄漏孔附近产生负压波，加上环境噪声、管道中的不连续结构产生的噪声，这些信号被传感器接收，它们在空间上是分散的，满足信号源之间相互独立的约束条件，虽然均值不为零，但是只需要简单的数学处理(去均值化)[17]即可，不影响判断结果。此方法应用时的另一个关键问题是原始信号源的数目无法确定，并且实际管道结构复杂，噪声来源较多。但是，实际对泄漏信号产生干扰的强烈信号源数目并不多，并且可将信号归为有用信号和噪声信号两大类，满足源信号数目不大于观测信号数目的约束条件。

为探究此方法的准确性，在小波去噪之后的压力信号中分别加入(a)、(b)、(c)三种已知噪声(见图8)，这三种噪声满足均值和方差都相同。

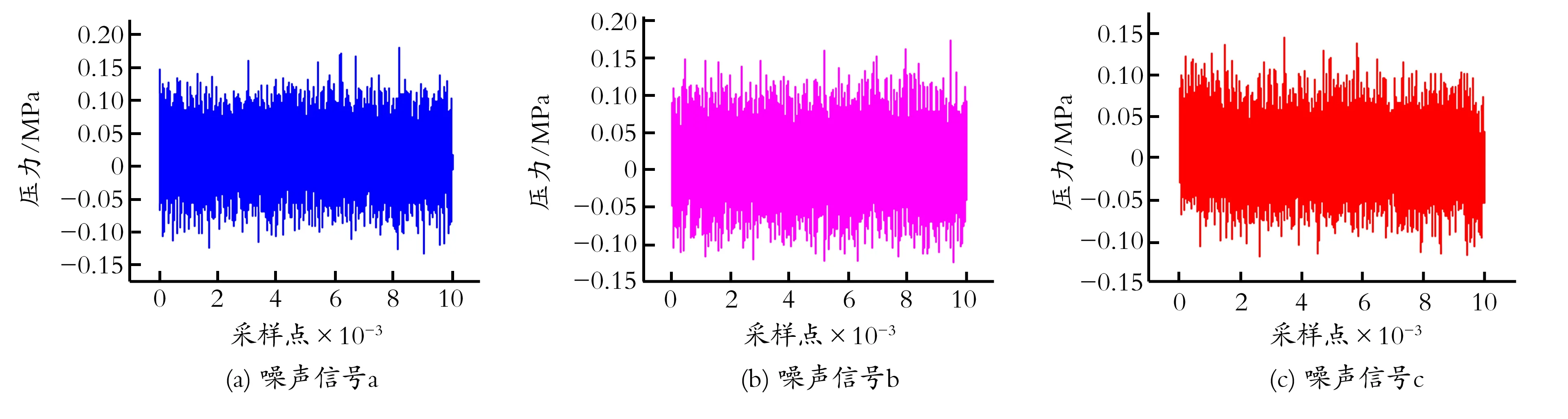
图8 噪声信号

Fig.8Noisesignal

分别对加入已知噪声的三个混合信号进行盲源分离，观测分离后信号的实际效果，其结果如图9所示。

Fig.9Theseparationeffectdiagramofnoisysignal

从图9可以看出，对于已知组成的三组信号，运用该方法得出的泄漏信号基本完成了源信号的复原，只是在波形细节处理上有些许不同，这是由于分离时信号的零均值和单位方差所致。由于三组信号的泄漏信息相同，不同的加噪处理之后分离的泄漏信号基本相同，计算利用盲源分离得到的泄漏信号的信噪比分别为53.6、50.7、52.1，均方根误差分别为3.58×10-3、3.32×10-3、3.75×10-3，此方法的消噪效果要优于时频联合去噪。

4 结论

(1) 通过时频联合分析表征了泄漏信号传播过程中的能量衰减，从两方面阐述了实际工程中小泄漏不易被发现的原因。

(2) 采用加权平均法改进小波阈值函数，提高了小波去噪的重构精度，并从数学角度分析了新阈值函数的可行性与优越性。

(3) 在改进小波阈值函数的基础上，将小波变换与基于最大信噪比的盲源分离方法相融合，通过分离已知构造信号说明此方法的适用性，验证该融合算法的实际去噪效果和工业应用价值。

[1] 殷新宇. 小波分析在管道损伤检测中的应用[D].西安：西安科技大学,2007.

[2] 柳艳红,魏学业,王大虎. 一种新型的基于相关特性的信号重构算法[J]. 仪器仪表学报,2006,27(5):466-469.

Liu Y H, Wei X Y, Wang D H. A new signal reconstruction algorithm based on correlation characteristics[J]. Chinese Journal of Scientific Instrument, 2006,27(5):466-469.

[3] 王辉. 输油管道微小泄漏特征提取方法研究[D].大庆：大庆石油学院,2008.

[4] 夏海波,张来斌,王朝晖,等. 小波分析在管道泄漏信号识别中的应用[J]. 石油大学学报(自然科学版),2003,27(2):78-80.

Xia H B, Zhang L B, Wang Z H, et al. Application of wavelet transform to signal detection of pipeline leakage[J]. Journal of the University of Petroleum, China, 2003,27(2):78-80.

[5] 余东亮,张来斌,梁伟,等. 长输管道信号降噪及工况识别方法研究[J]. 石油学报,2009,30(6):937-941.

Yu D L, Zhang L B, Liang W, et a. Noise reduction of signal and condition recognition of long-distance pipeline[J]. Acta Petrolei Sinica, 2009,30(6):937-941.

[6] 曹康,姜峰,郑运虎. 基于熵权模糊综合评价法的油气长输管道风险评估[J]. 辽宁石油化工大学学报, 2015, 35(5): 27-30.

Cao K， Jiang F， Zheng Y H. Study on oil and gas pipeline risk assessment based on entropy weight fuzzy comprehensive evaluation method[J]. Journal of Liaoning Shihua University, 2015, 35(5): 27-30.

[7] 关键. 基于BP神经网络的管道泄漏定位系统研究[D].北京：北京交通大学,2009.

[8] 周维忠,冯心海,孙国基. 基于小波系数聚类的特征提取分类方法[J]. 计算机研究与发展, 2001,38(8):982-987.

Zhou W Z, Feng X H, Sun G J. Classification based on feature extraction from cluster of wavelet coefficient[J]. Journal of Computer Research and Development, 2001,38(8):982-987.

[9] 赵瑞珍,宋国乡. 一种基于小波变换的白噪声消噪方法的改进[J]. 西安电子科技大学学报(自然科学版), 2000, 27(5):619-622.

Zhao R Z, Song G X. An improved method for white noise reduction based on wavelet transform[J]. Journal of Xidian University，2000，27(5)：619-622.

[10] 孟令雅,刘翠伟,刘超,等. 基于特征量提取的输气管道微泄漏检测[J]. 中国石油大学学报(自然科学版),2014,38(6):153-160.

Meng L Y, Liu C W, Liu C. et al. Characteristics extraction of acoustic leakage signal for natural gas pipelines[J]. Journal of China University of Petroleum (Edition of Natural Science), 2014,38(6):153-160.

[11] 孙禹楠,王岳. 燃气管道的动态泄漏研究[J]. 辽宁石油化工大学学报, 2017, 37(1): 30-33.

Sun Y N,Wang Y. Study on dynamic leakage of gas pipeline[J]. Journal of Liaoning Shihua University, 2017, 37(1): 30-33.

[12] 方韶茂. 盲信号分离算法及关键技术应用研究[D].广州：华南理工大学,2011.

[13] 李树钰. 小波和盲源分离融合技术在管道泄漏检测中的应用研究[D].西安：西安石油大学,2010.

[14] 李树钰. 改进的小波阈值去噪方法及其在MATLAB中的仿真[J]. 噪声与振动控制,2010,30(2):121-124.

Li S Y. Improved wavelet threshold denoising method and its simulation using MATLAB[J]. Noise and Vibration Control,2010,30(2):121-124.

[15] 王蓓,张根耀,李智,等. 基于新阈值函数的小波阈值去噪算法[J]. 计算机应用,2014,34(5):1499-1502.

Wang B, Zhang G Y, Li Z, et al. Wavelet threshold denoising algorithm based on eew threshold function[J]. Journal of Computer Applications,2014,34(5):1499-1502.

[16] 刘洋. 基于最大信噪比的盲源分离算法及在振动信号中的应用研究[D].武汉：武汉理工大学,2011.

[17] 殷琴. 盲源分离算法在管道泄漏检测中的应用研究[D].大庆：东北石油大学,2013.