交叉口信号优化控制的深度循环Q学习方法

施赛江，陈 锋

(中国科学技术大学 信息科学技术学院，安徽 合肥 230027)

0 引言

随着我国经济的快速发展，交通拥堵问题已经非常严重，对国家造成了很大的经济损失。大力发展智能交通，利用人工智能领域的知识，加强对城市交通信号的有效控制，可以有效缓解城市拥堵。调查统计发现，大部分交通拥堵发生在交叉口，所以对城市交叉口采用更加智能的控制策略尤为关键。

采用强化学习方法对交叉口进行优化配时已经取得了很好的效果[1-3]。为了加快Q学习的收敛速度，引入模糊学习[4]对Q函数进行初始化，减少了Q学习的训练时间。但是强化学习的状态空间不能太大，否则会出现维度爆炸的问题，所以状态都采用低维人工特征，遗失了有用信息。

随着近年深度学习的快速发展，MNIH V等人[5]最初提出深度Q学习(Deep Q Network,DQN)，之后又对DQN进行完善，在DQN的训练过程中引入了经验池回放技术和目标网络的概念[6]。

已经有研究将DQN应用于交叉口的配时中，文献[7]采用SAE网络去估计Q值；文献[8]和文献[9]用深度卷积神经网络表示Q值，将交叉口车辆的位置、速度用矩阵表示；文献[10]除了使用车辆的位置和速度矩阵外，还加入了车辆的加速度矩阵作为交叉口的状态，取得了一定的效果。但是，文献[11]证明了单交叉口的状态是部分可观测马尔科夫的(Partially Observable MDP，POMDP)，本文为了进一步降低交叉口的POMDP特性对深度Q学习性能的影响，对深度神经网络结构进行改进，将深度循环Q学习(Deep Recurrent Q Network,DRQN)引入交叉口的配时中，同时本文针对上述研究中动作空间较小的缺陷，增大了动作空间。实验表明，改进动作空间后的DRQN表现要比DQN好，并且优于传统的交叉口控制方法定时控制和Q学习控制。

1 Q学习算法

Q学习由如下过程来描述：智能体在环境中，状态空间为S，可以采用的动作空间为A，根据概率转移矩阵P使得状态从当前状态转移到下一个状态，同时得到奖赏R，状态到动作的Q值用Q(s,a)表示。

假设智能体在时刻t的状态是st，智能体采取的动作是at，智能体执行动作后状态转移到下一个t+1时刻，状态为st+1，得到的奖赏是rt，那么智能体根据所有的记录(st,at,rt,st+1)更新Q(s,a)的值，从而找到最优策略。

本节针对本文研究的单交叉口，将分别定义Q学习中的状态、动作和奖赏函数。

1.1 状态空间

考虑如图1所示的四相位的单交叉口，以当前路口四个相位的车辆的位置、速度、加速度矩阵作为输入。

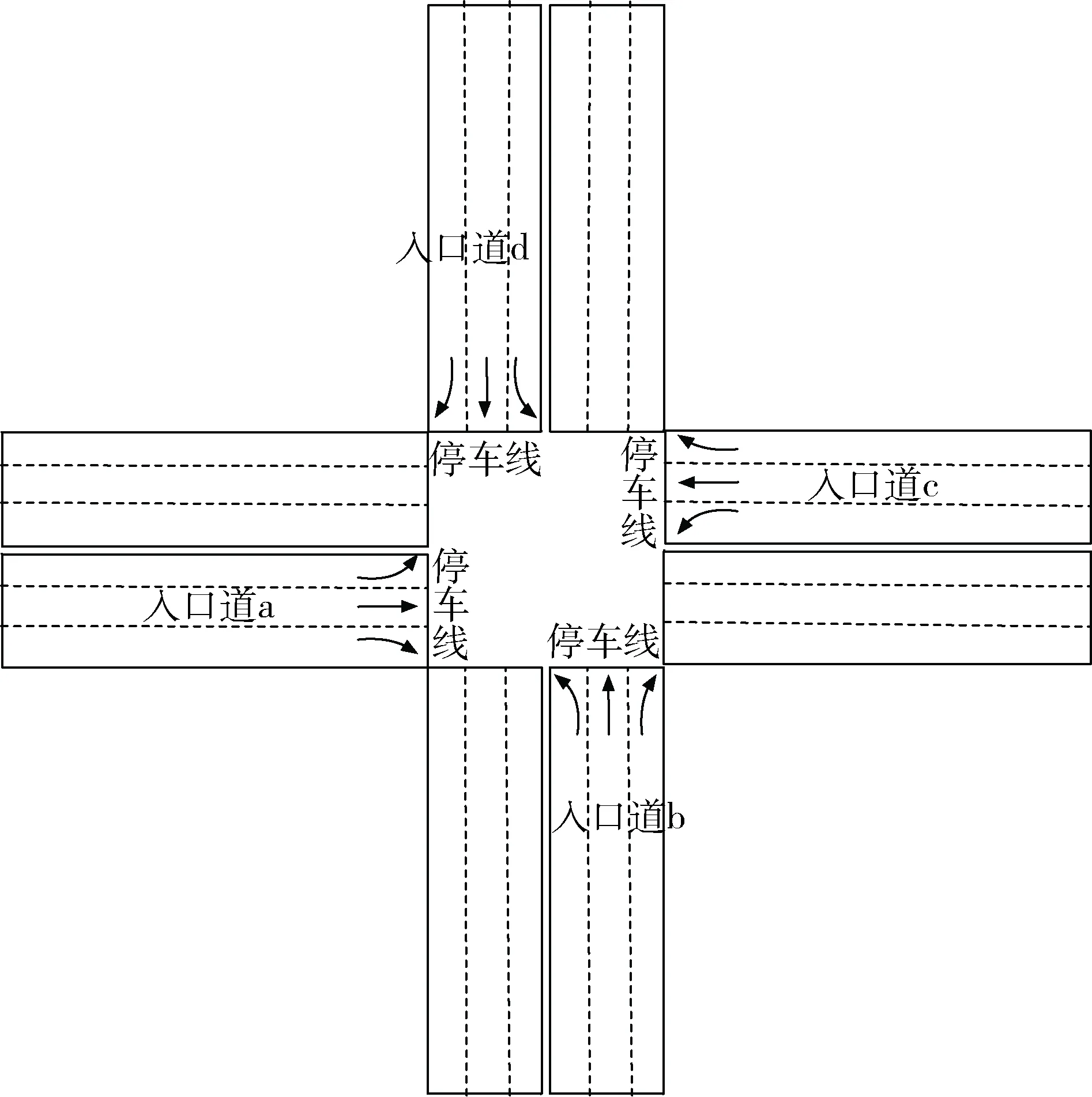
图1 四相位交叉口示意图

以图1中入口道a为例，假设当前路口车辆如图2所示，考虑离停车线的距离为L的路段，将道路划分为多个小路段，称为Cell，每个Cell的长度是C，那么当前路口车辆的位置、速度、加速度矩阵如表1～表3所示。当某一辆车跨过两个Cell时，选择占用比例大的那个Cell，速度矩阵、加速度矩阵和位置矩阵对应，矩阵的值经过归一化得到。

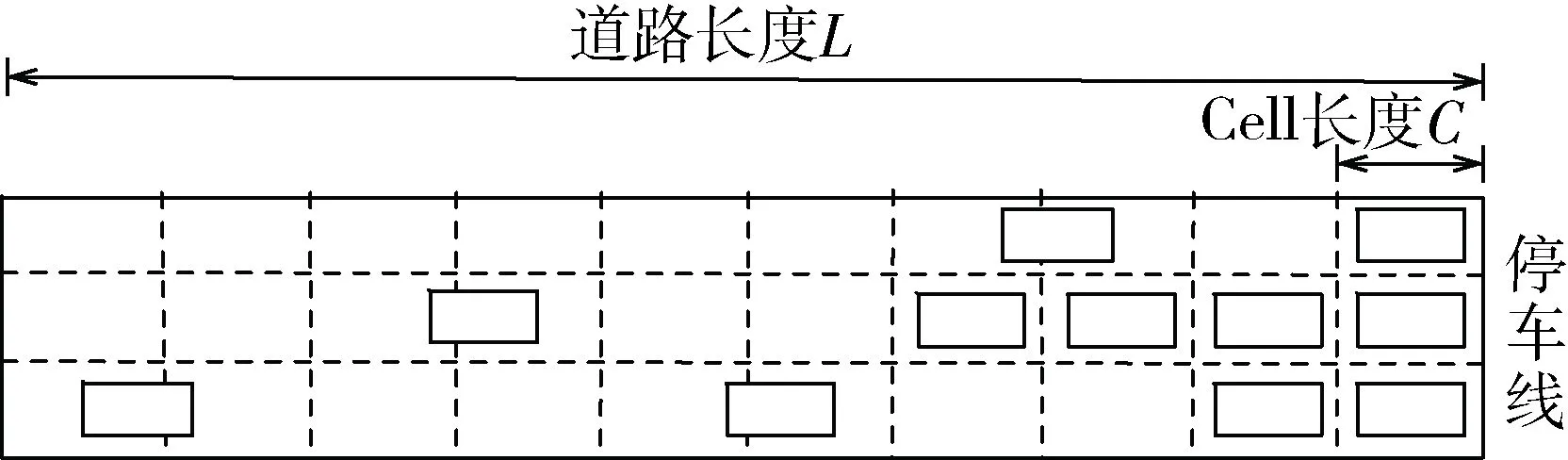
图2 入口道a车辆位置示意图

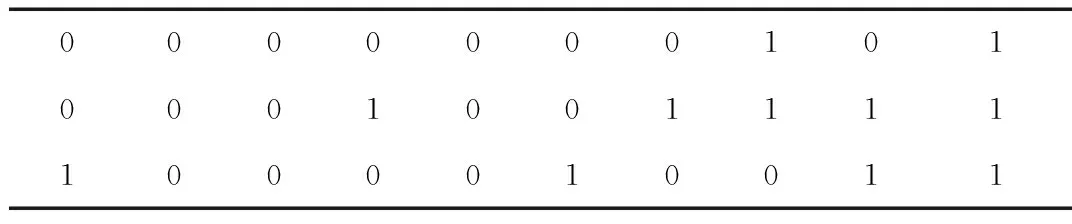
000000010100010011111000010011

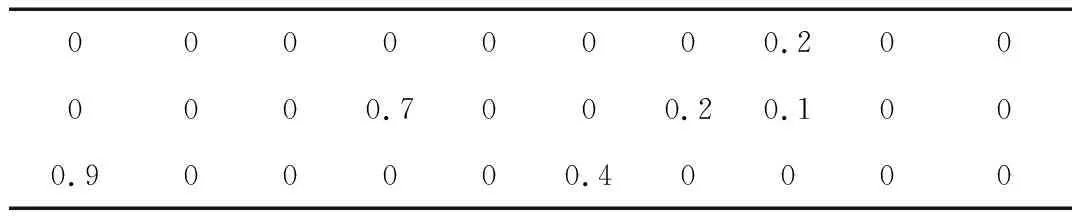
表2 入口道a车辆速度矩阵

表3 入口道a车辆加速度矩阵

1.2 动作空间

当智能体观测到状态之后，需要在动作空间中选择一个动作去执行，在每个时刻选择最优的动作即为交叉口的信号控制优化，交叉口的信号控制优化可以分为相序优化和配时优化两种[1]。

当前将深度Q学习应用于单交叉口信号优化的研究都采用的是相序优化[8-10]，本文将相序优化和配时优化结合，在优化相序的同时使得每个相位的时间可选。本文假设右转车辆常绿的情况下，四个相位分别是东西相位直行、东西相位左转、南北相位直行、南北相位左转，同时，增加这四个相位的配时时间，考虑到实际中配时不能太短也不能太长，故本文选择配时为10 s～49 s 之间任意整数值，这样动作空间将是160维。

固定配时时间的方案中，仅仅是对相序进行调整，最终配时将会是设定的固定配时的整数倍，会遗漏最优动作解。采用本文的配时方案，增加了动作空间，在四相位不变的基础上对每个相位增加可选时间，此时Agent不会错过最优动作解，同时160维动作空间大小也符合神经网络的输出层的大小要求。

1.3 奖赏函数表示

Q学习会根据奖赏函数来迭代训练，平均延误能够表示当前路口的拥堵情况，故本文采用平均延误作为奖赏函数的评价指标，这里平均延误用D表示，假设t时刻的平均延误为dt，t+1时刻的平均延误为dt+1，奖赏函数为rt+1，则：

rt+1=-(dt+1-dt)

(1)

延误变小，则rt+1>0，代表奖赏；延误变大，则rt+1<0，代表惩罚。

2 神经网络结构

2.1 网络结构

Q学习方法采用表格或者函数逼近器来表示Q(s,a)的值，深度Q学习采用更深层的神经网络结构表示Q(s,a|θ)的值，这里θ代表神经网络的权值，本节将会介绍具体的网络结构。

当前的研究采用卷积神经网络和全连接神经网络结合的方式构建DQN，但是由于路口的POMDP特性导致DQN的性能降低，定义POMDP中观测状态是O，那么O和真实状态S是不同的,即Q(s,a|θ)!=Q(o,a|θ)。

本文引入DRQN，DRQN已经被证明可以很好地处理POMDP问题[12]。DRQN中包含了循环神经网络层LSTM(Long Short-Term Memory)，LSTM细胞状态的设计可以记住时间轴上长期的历史信息，所以LSTM已经在处理时间序列的问题中取得了很大的成功。

利用LSTM能够记忆时间轴信息的特性，通过记忆前几个时刻的输入状态，而不是仅仅通过当前时刻的状态，尽可能完全地表示当前交叉口的输入状态，减少Q(s,a|θ)和Q(o,a|θ)之间的差距，从而可以处理部分可观测马尔科夫问题，提高DQN算法的性能。

接下来介绍DRQN的网络结构，使用卷积神经网络和循环神经网络相结合来表示Q函数，将状态矩阵连接具有两层卷积层的卷积神经网络，激活函数采用ReLU，后面是用ReLU激活的LSTM层，LSTM层的层数和每层神经元的个数需要经过实验确定，最后的输出层是全连接层，用于将前面网络提取的高维特征空间映射到低维的动作空间，输出的是所有动作的Q值。网络结构如图3所示。

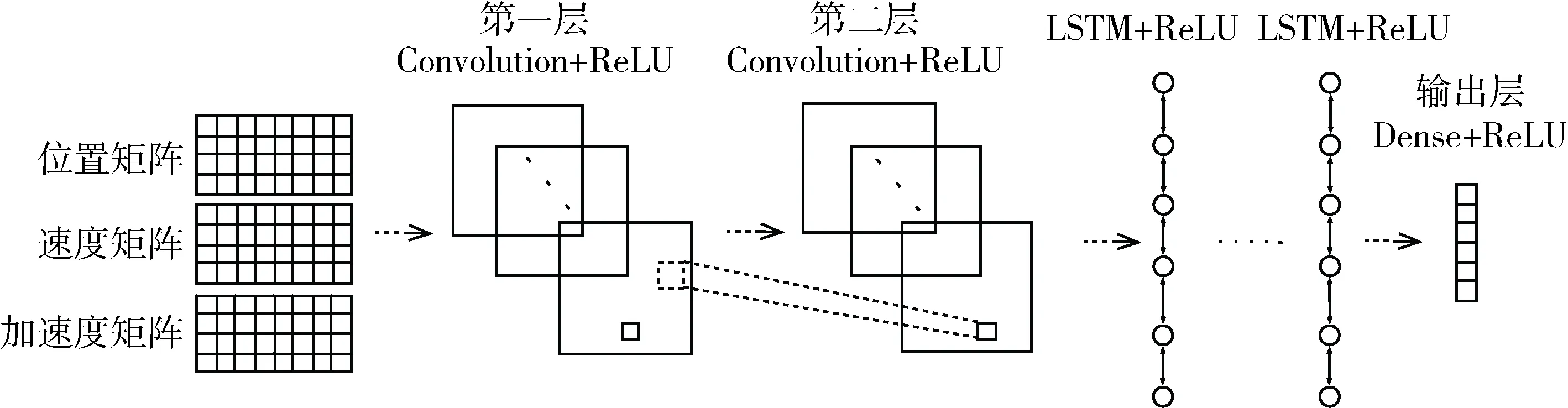
图3 DRQN网络结构

2.2 训练方法

如第1节所述，强化学习在状态转移过程中产生很多组纪录(st,at,rt,st+1)，根据这些纪录构建深度神经网络的训练样本，神经网络的输入为st，输出是目标Q值：

yt=rt+γmaxat+1Q(st+1,at+1|θ)

(2)

式中γ是折扣因子，θ是深度Q网络的权值。

定义误差是均方根误差MSE：

L(θ)=E[(rt+γmaxat+1Q(st+1,at+1|θ)-Q(st,at|θ))2]

(3)

采用Adam算法进行网络的训练。

为了使得深度神经网络能够更快地收敛，在训练过程中采用目标网络和经验池回放技术[6]，同时为了避免算法陷入局部最优，采用ε贪心策略。ε会随着训练次数而逐渐衰减：

(4)

其中，N是总的训练次数，n是当前训练次数。

2.3 DRQN算法步骤

DRQN算法步骤如下:

1： 初始化DRQN网络结构，参数为θ；初始化目标网络，参数为θ′=θ

2： 初始化ε,γ,N

3： for 1 到Ndo

4： 初始化交叉口状态s0，初始化动作a0

5： for 1 到Tdo

6： 以1-ε的概率选择at=argmaxaQ(st,a|θ)，以ε的概率随机选择一个动作at

7： 执行选择的动作at，得到奖赏rt和下一个状态st+1

8： 将此经验(st,at,rt,st+1)存入经验池M中

9： 如果经验池中样本数目达到batch：

10： 随机从经验池中取出batch大小的样本，对每一条记录，根据目标网络得到:

y=rt+γmaxat+1Q(st+1,at+1|θ′)

11： 用随机梯度下降法Adam更新θ

12： 达到一定步数后更新θ′

13： 当前状态=新状态

14： end for

15： end for

3 仿真实验及分析

3.1 实验平台及参数设置

实验平台选择中国科学技术大学微观交通仿真平台2.1(USTC Microscopic Traffic Simulator2.1，USTCMTS2.1)，利用Python实现的深度学习库Keras搭建DRQN网络，两者的通信采用IronPython库。

参数设置：Q学习中折扣因子γ=0.95，循环次数N=200次，仿真中的T为0.1 h，L设置为224 m，C设置为7 m，经验池大小M=2 000，batch为32，两层卷积层的卷积核数目分别是32个和64个，卷积核大小为3*3，神经网络的学习率为0.001。

路口流量设置：流量采用无锡市滨湖区梁清路和鸿桥路交叉口2017年7月3日的流量数据，取其中有代表性的时间点08:00、11:00和23:00，此时的流量分别对应过饱和度流量、近饱和度流量和低饱和度流量，具体数值见表4。

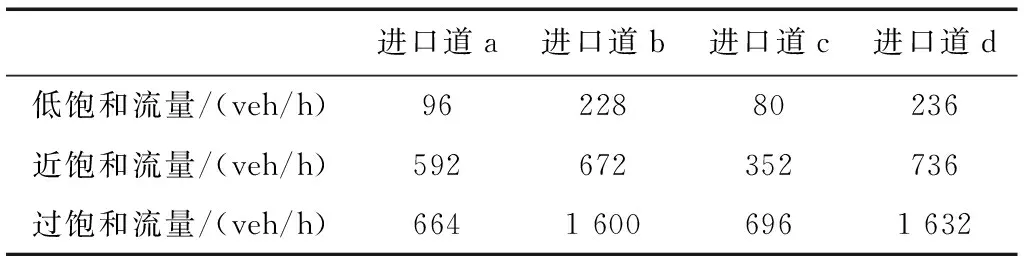
表4 三种饱和度流量各个进口道流量值

3.2 结果讨论

3.2.1不同流量情况下网络结构确定

针对3.1节中典型的3种不同饱和度流量，本小节为这3种饱和度流量分别确定LSTM层的层数和神经元个数。根据深度学习中的参数设置经验，选择网络的层数从1到3层，神经元个数分别是{64，128，256，512}，采用网格搜索，得到3种流量在不同的网络参数下的平均延误如表5～表7所示。

表5 低饱和度流量不同网络参数下平均延误表(s)

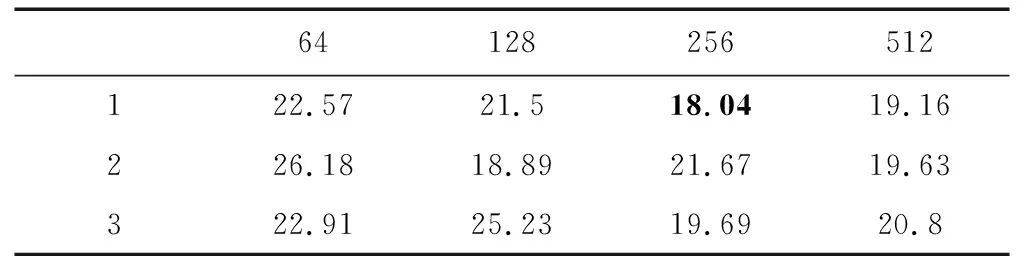
表6 近饱和度流量不同网络参数下平均延误表(s)

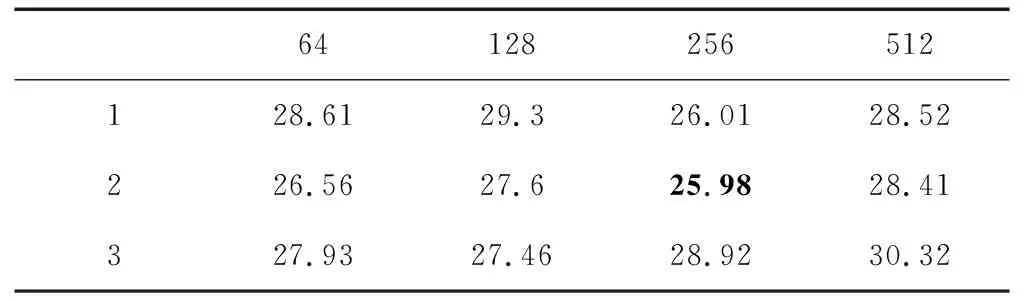
表7 过饱和度流量不同网络参数下平均延误表(s)

从表中可以看出，低饱和度流量下最优的网络结构是2层LSTM层，每层包含128个神经元，近饱和度流量下最优的网络结构是1个LSTM层，每层包含256个神经元，而过饱和度流量下最优的网络结构是2个LSTM层，每层256个神经元。

3.2.2不同网络结构下性能对比

以图1所示的交叉口为实验对象，以表4中近饱和度流量为例，分析本文提出的DRQN的表现。网络结构采用3.2.1小节中表6所示的最优的网络结构，得到原始DQN的平均延误为19.22 s，DRQN的平均延误为18.04 s，发现DRQN的平均延误比原始DQN减少了6.1%。图4是DRQN和Q学习(Q Learning,QL)以及定时控制(Fixed Timing,FT)的对比，横坐标是仿真时间T，纵坐标是平均延误D，Q学习和定时控制的平均延误是20.88 s和21.24 s，DRQN与这两种算法相比，平均延误分别减少了13.6%和15.1%，说明循环神经网络记录的历史信息确实使得观测的状态更加符合真实交叉口状态。

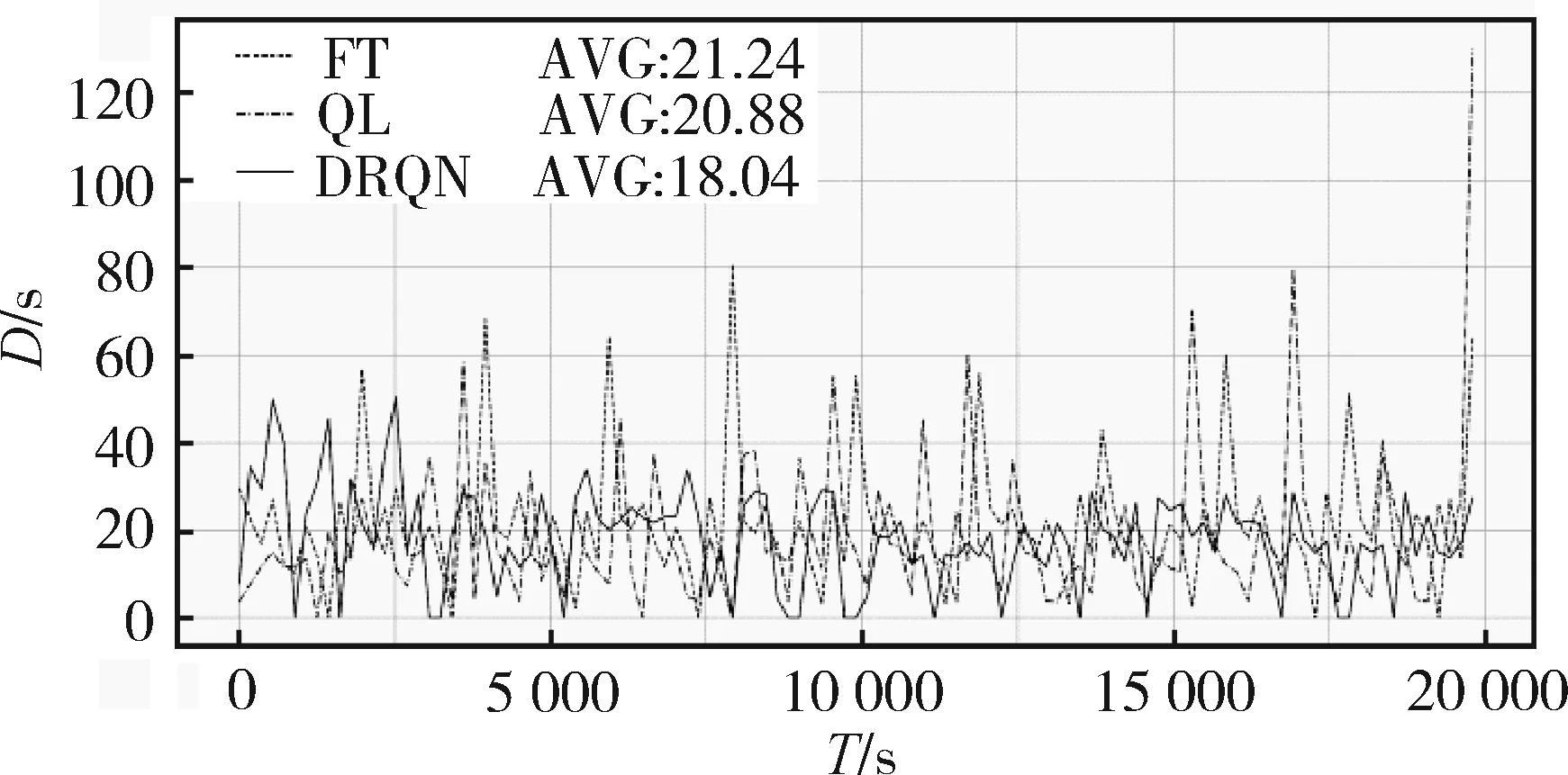
图4 三种算法平均延误对比图

接下来通过实验确定改进动作空间后的DRQN(用DRQN-A表示)和DRQN的对比。从图5可以看到，增大动作空间后，在相同的网络结构下平均延误降低了6.7%，说明交叉口从动作空间中选择了更好的动作。

图5 DRQN和DRQN-A平均延误对比图

以上是对近饱和流量的情况下进行的对比试验，对3.1小节中其他两种饱和度流量进行实验，网络结构均为3.2.1小节中最优的网络结构，平均延误见表8。

表8 低饱和度和过饱和度平均延误对比表 (s)

当取另外两种不同的饱和度时，结果与近饱和时类似，原始DQN的平均延误都要比定时控制和Q学习的平均延误小,DRQN算法平均延误也比原始DQN小，改进动作空间后，DRQN的性能也有提升，故本文提出的算法是有效的。

4 结束语

本文针对单交叉口的部分可观测马尔科夫特性对深度Q学习性能的影响，通过引入循环神经网络，对深度Q学习网络进行改进，利用LSTM记忆时间轴信息的特性，使得交叉口的状态更接近于完全可观测马尔科夫，同时考虑到动作空间太小不利于交叉口找到最优动作的情况，增大了动作空间。实验表明，本文提出的改进动作空间的DRQN算法在不同饱和度流量情况下比DQN算法都有提升，也优于传统的定时控制和Q学习算法。未来的工作可以将单交叉口扩展到局部路网，研究DRQN在局部路网中的表现。

[1] PRABUCHANDRAN K J, AN H K, BHATNAGAR S. Decentralized learning for traffic signal control[C]//2015 7th International Conference on Communication Systems and Networks (COMSNETS). IEEE, 2015: 1-6.

[2] AREL I, LIU C, URBANIK T, et al. Reinforcement learning-based multi-agent system for network traffic signal control[J]. Intelligent Transport Systems IET, 2010, 4(2):128-135.

[3] 马跃峰, 王宜举. 一种基于Q学习的单路口交通信号控制方法[J]. 数学的实践与认识, 2011, 41(24):102-106.

[4] 聂建强, 徐大林. 基于模糊Q学习的分布式自适应交通信号控制[J]. 计算机技术与发展, 2013, 23(3):171-174.

[5] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing atari with deep reinforcement learning[C]//Proceedings of Workshops at the 26th Neural Information Processing Systems， 2013. Lake Tahoe, USA, 2013:201-220.

[6] MNIH V, KAVUKCUOGLU K, SILVER D, et al. Human-level control through deep reinforcement learning[J]. Nature, 2015(7540):529-533.

[7] Li Li, Lv Yisheng, Wang Fei yue, et al. Traffic signal timing via deep reinforcement learning[J]. IEEE/CAA Journal of Automatica Sinica, 2016, 3(3):247-254.

[8] GENDERS W, RAZAVI S. Using a deep reinforcement learning agent for traffic signal control[J]. arXiv preprint arXiv:1611.01142, 2016.

[9] GAO J, SHEN Y, LIU J, et al. Adaptive traffic signal control: deep reinforcement learning algorithm with experience replay and target network[J]. arXiv preprint arXiv:1705.02755, 2017.

[10] Van der Pol E. Deep reinforcement learning for coordination in traffic light control[D]. Master’s thesis, University of Amsterdam, 2016.

[11] RITCHER S. Traffic light scheduling using policy-gradient reinforcement learning[C]//The International Conference on Automated Planning and Scheduling, ICAPS, 2007.

[12] HAUSKNECHT M, STONE P. Deep recurrent Q-learning for partially observable MDPs[J]. arXiv: 1507.06527.