变参数深度玻尔兹曼计算模型研究

王 娜，陈贤富

(中国科学技术大学 信息科学技术学院，安徽 合肥 230027)

0 引言

人类认知具有层次性[1]，这种层次结构性大大简化了问题求解的复杂性，提高了认知的敏捷性与智能性。基于层次性认知以及非监督学习等技术发展，深度学习技术近年来在数据挖掘、自然语言处理、视音频智能信息处理等智能认知领域取得重要突破，迅速成为IT技术前沿研究热点。

从计算机理看，机器学习可看成特征参量关系模型的拟合与优化过程，优化与学习的机制机理是相通的，联想、优化本质上也是一种学习。为此，本文将深度学习Dropout等技术与模拟退火算法相结合，提出一种变参数深度玻尔兹曼计算模型，并主要针对复杂TSP优化问题开展了具体算法研究与实验研究。

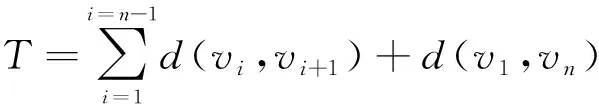
TSP问题是典型NP_Hard型问题，其可行解空间规模为n!/2。鉴于TSP问题的组合爆炸性质，除极小规模TSP问题外，一般情形只能采用启发式智能算法进行搜索优化求解。流行实用的TSP全局优化算法主要有模拟生物演化、模拟热处理退火及各种混合型算法。其中，模拟生物演化型算法又可分为基因重组型(遗传算法、进化策略等)与集群智能型(蚁群算法[4]、鸟群算法、鱼群算法等)两大类，在求解TSP问题中主要存在基因型重组与表现型评估矛盾、空间复杂度较高、遗传支配、早熟收敛、有序问题的遗传操作设计、局部搜索与全局优化矛盾等问题。为解决粗粒度全局搜索与细粒度局部优化之间的矛盾，分层混合算法结构虽已成为一种流行的改进思路，但有序问题编码设计及其遗传操作问题、空间复杂度较高、遗传支配个体垄断群体更新策略等原因导致的早熟收敛等问题仍然存在，规模效应问题依然突出。

模拟退火算法[5-6]是一种细粒度的基于表现型评估的全局搜索优化算法，也是公认的解决TSP问题较合适的算法之一。理论上说，模拟退火是一标准马尔可夫过程，在充分搜索、合理选择、缓慢降温等条件下以概率1收敛于全局最优解。实际上，由于无法满足理想的充分搜索、缓慢降温等条件，模拟退火算法设计依然只能在全局搜索与局部优化、较好的优化效果与较快的搜索效率之间进行权衡，其随机搜索轨迹由初态与一系列转移概率矩阵确定:

π=π0*[p1]n*[p2]n*[pk]n

(1)

其中π0为初始状态，[pk]为一步转移概率矩阵。

模拟退火算法搜索优化性能由初始状态与一步转移概率矩阵决定，其中决定一步转移概率矩阵参数的除了温度、玻尔兹曼模型参数外，还与所需求解具体问题的参量分布密切相关。流行的模拟退火算法研究主要集中于SA模型参数的变化与初始状态的选择策略方面，对问题参数扰动所产生的影响尚缺乏充分研究考量。

一方面，变参数动态优化问题本身就是优化应用领域的前沿热点课题；另一方面，从动态变化角度研究静态最优化问题也不失为一种合理可行的优化算法改进思路。鉴于这些研究考虑，本文提出并研究一种基于深度学习的层次结构与Dropout技术的变参数并行玻尔兹曼算法模型，并结合TSP优化问题介绍具体研究思路与算法模型设计。

1 变参数玻尔兹曼算法模型设计

鉴于TSP问题的可行解空间规模为n!/2，规模较大的TSP局部优化问题实际上也是较复杂的全局性搜索问题。根据式(1)，通过选择合适的初始状态，模拟退火算法模型参数的合理设计以及问题参量的扰动等手段，进一步提高模拟退火算法的优化质量。

有鉴如此，变参数分层玻尔兹曼优化算法模型框架主要由三部分组成。其一为全局优化，可采用模拟退火或模拟演化等全局优化算法模型实现，初步获取若干高质量全局较优可行解，为进一步分层优化、变参数优化提供基本参考数据。本文采用常规SA算法产生初步全局可行解，具体算法流程如图1所示。其二，为克服SA算法陷入局部陷阱，拟采用深度学习中的Dropout、Dropin等策略，实现变参数扰动。Dropout等深度学习技术[7]可用于防止过拟合学习、简化模型结构以及降低算法复杂度等方面。考虑到TSP问题与神经网络存在结构相似性、机理相关性，故在TSP优化过程中，使较优可行解上某相邻两个城市间的距离扩大到一定值，使该条路径成为不经之路(dropout)，或使某相邻两个城市间的距离缩小到一定值，使该条路径成为必经路径(dropin)，运用变参数动态优化策略以期跳出局部陷阱。其三，鉴于大规模TSP问题优化的复杂度高，其局部片段优化也是全局性较高的优化子问题，可采用分段优化策略[8]，进一步提高优化质量。

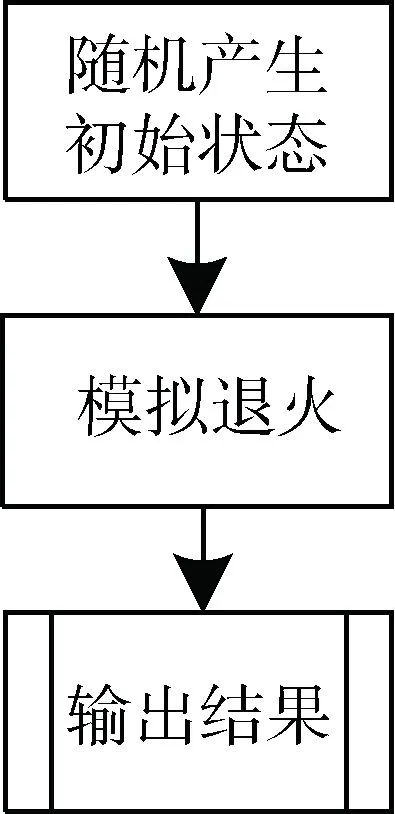
图1 模拟退火算法流程图

2 算法设计与实验研究

2.1 Drop算法设计

Drop边的选择策略可采取以下几种方式：

(1)随机选择路径中某条边进行缩放，该策略盲目性较大，算法复杂度过高。

(2)从若干较优路径中选择某一公共边或不同边进行缩放，可使算法兼顾搜索效率与优化效果。

(3)人机交互，人眼观察若干较优路径图，运用人类智慧选取某条边进行缩放。

实验研究中，本文采用了上述策略(2)与策略(3)Drop学习技术，其算法流程图如图2与图3所示。

图2 本文算法流程图

图3 Dropout 具体算法流程图

2.2 分段优化

为进一步提高优化质量，在获得原问题的一个高质量可行解后，再通过分段优化算法进行局域精细优化，具体算法流程如图4所示，其中分段选择的策略如下：

(1)随机分段

随机选择路径中某一起点，该起点后的若干城市作为一个局部片段进行优化。

(2)人机交互

人眼观察若干较优路径图，根据城市坐标的结构特征，由内到外进行局部片段的选择。

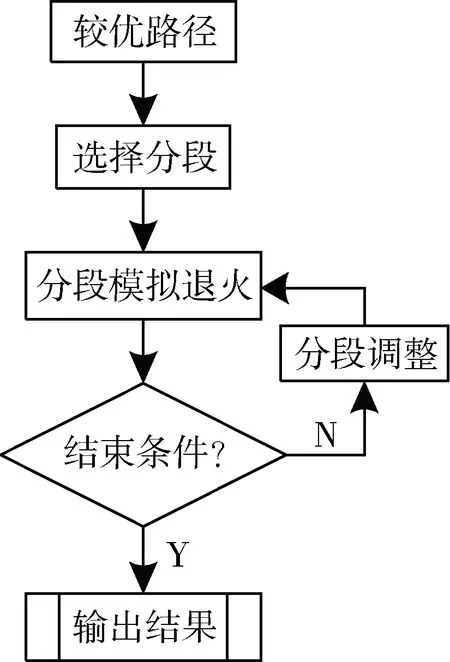
图4 分段算法流程图

3 实验结果与分析

为验证算法的有效性，选用了国际上通用的TSP测试库[9]TSPLIB中多个实例进行测试。实验环境为Inter(R) Core(TM)i5-4590 CPU @3.30 GHz、Windows 7、Visual Studio 2010。

本文对TSPLIB中eil50、eil51、eil75、eil76实例进行了实验，其中eil50、eil51、eil75、pr1002城市TSP均搜索到迄今已知最优路径[10]，其中eil51城市，本算法搜索到了新的、比迄今已知最优解更优的TSP路径(浮点计算)，实验结果和路径图如表1和图5～9所示。

表1 TSPLIB提供的路径值与本文算法所得最优路径比较表

图5 本文算法得到的eil51实例最优路径图d=428.329

图6 TSPLIB提供的eil51实例最优路径图d=429.983

图7 本文算法得到的eil76实例最优路径图d=544.369

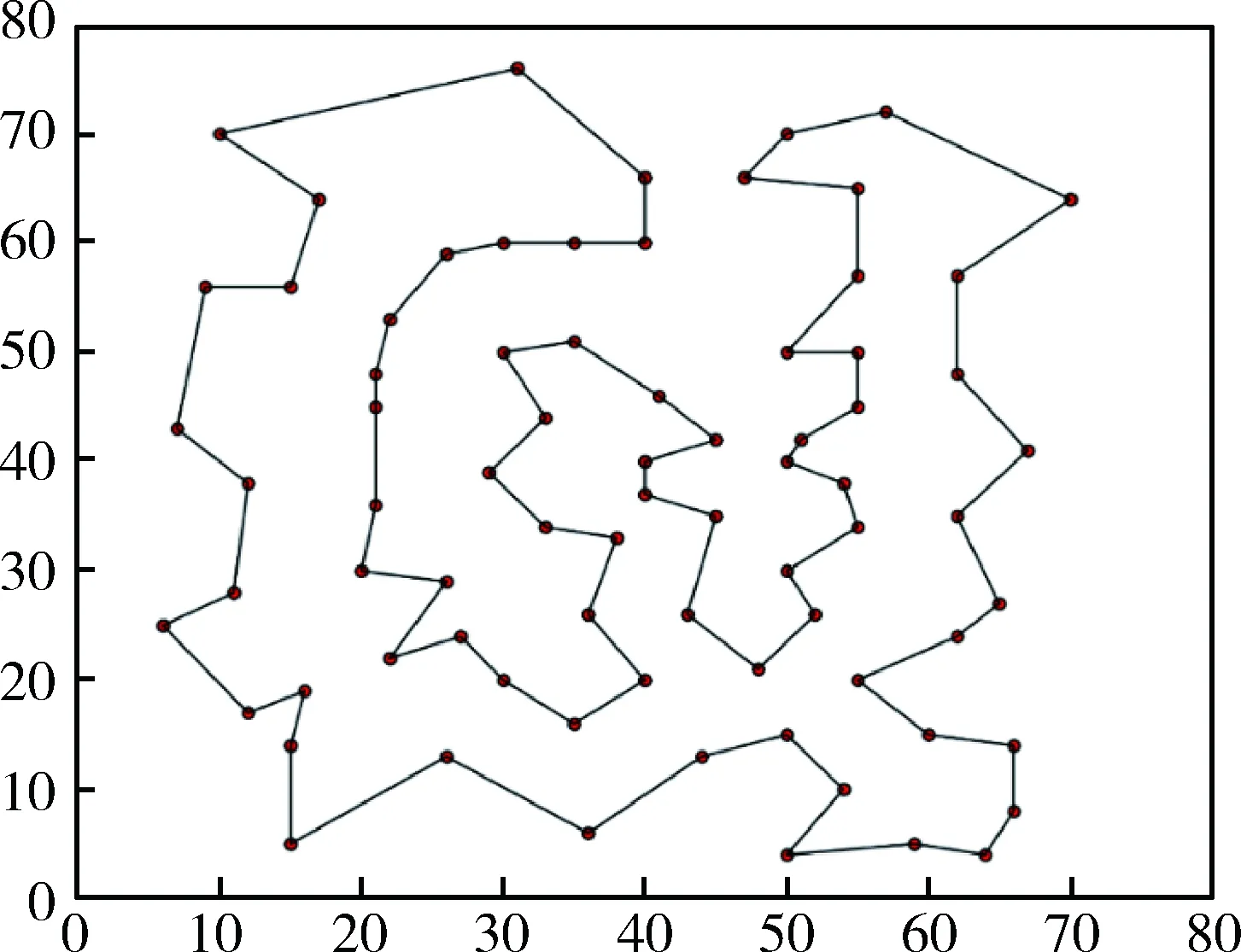
图8 TSPLIB提供的eil76实例最优路径图d=545.388

图9 pr1002实例经过本文算法得到的最优路径图d=259 066.663

本文算法所得城市TSP最优路径如下：

eil51城市TSP: 路径长度=428.328 712

(30,48) (38,46) (37,52) (42,57) (49,49) (52,41) (56,37) (52,33) (48,28) (45,35) (40,30) (42,21) (36,16) (39,10) (46,10) (59,15) (51,21) (58,27) (61,33) (62,42) (58,48) (57,58) (62,63) (63,69) (52,64) (43,67) (37,69) (27,68) (31,62) (25,55) (21,47) (16,57) (17,63) (5,64) (8,52) (12,42) (7,38) (5,25) (10,17) (5,6) (13,13) (21,10) (30,15) (32,22) (27,23) (20,26) (17,33) (25,32) (31,32) (32,39) (30,40)

4 结论

本文提出并初步研究了一种基于深度学习之层次

结构与Drop技术的变参数玻尔兹曼算法模型，并通过TSP优化实例展示了良好的优化性能与优化结果。本文提出并研究的若干算法设计思路还可应用于动态TSP优化、神经学习、联想记忆等其他领域，具体算法模型有待进一步探索研究。

[1] MASLOW A H.A theory of human motivation[J]. PsychologicalReview,1943,50(8):370-396.

[2] GAREY M R, JOHNSON D S. Computers and intractability:a guide to the theory of NP-completeness [M]. San Francisco: Freeman W H, 1979.

[3] 陈贤富，庄镇泉，王煦法，遗传算法的自适应进化策略及TSP问题的遗传优化[J].电子学报, 1997，25(7)：111-114.

[4] 许凯波, 鲁海燕, 程毕芸, 等. 求解TSP的改进信息素二次更新与局部优化蚁群算法[J]. 计算机应用, 2017, 37(6): 1686-1691.

[5] 张盛意，蔡之华，占志刚.基于改进模拟退火的遗传算法求解0-1背包问题[J].微电子学与计算机，2011，28(2)：61-64.

[6] 何庆, 吴意乐, 徐同伟. 改进遗传模拟退火算法在TSP优化中的应用[J]. 控制与决策, 2018,33(2):219-225.

[7] SRIVASTAVA N, HINTON G E, KRIZHEVSKY A, et al. Dropout: a simple way to prevent neural networks from overfitting[J].Journal of Machine Learning Research, 2014,15(1):1929-1958.

[8] 吴斌，史忠植.一种基于蚁群算法的TSP问题分段求解算法[J].计算机学报，2001,24(12)：1328-1333.

[9] 标准TSP测试库[EB/OL].[2018-02-26]http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsp/index.html.

[10] 标准TSP路径历史最优解[EB/OL].[2018-02-26]http://www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/STSP.html.