基于非光滑表面雨挡的汽车风振噪声动态计算分析与优化

宗轶琦, 谷正气, 罗泽敏, 江财茂, 张启东

(1.扬州大学 机械工程学院， 江苏 扬州 225127； 2.湖南大学 汽车车身先进设计制造国家重点实验室， 长沙 410082；3.湖南文理学院， 湖南 常德 415000； 4.广州汽车集团股份有限公司 汽车工程研究院， 广州 516434)

汽车在行驶过程中，由于天窗或侧窗打开，气流通过车身的开口处而产生具有一定传播速度的涡列，并与车内空间声模态耦合，交换能量从而形成风振噪声，这是一种频率很低但是强度很高的气动噪声[1]。这种噪声能够使乘客产生烦躁和疲劳感。因而，为了提高乘坐舒适性，在汽车的设计阶段，对某侧窗开度下的最大风振噪声进行预测与分析，进而采取相应的降噪措施，将有重要意义。

在风振噪声数值模拟研究中，较常用的研究方式是针对天窗或侧窗某一固定开度进行数值仿真计算。其中，Lemaitre等[2]对某轿车天窗风振噪声的宽频带特性进行了分析，进而根据风振的强度对心理声学响度指标进行了计算，并对乘员室内部人员由风振噪声引起的不舒适性进行新的评估。Mendonca[3]探索性地提出运用CFD/CAE混合计算方法来提高汽车风振噪声的计算精度，从而弥补以往计算过程中未考虑的结构刚度、内饰材料等因素。杨振东等[4]采用大涡模型与FW-H方程对汽车天窗风振噪声进行了数值模拟，分析与揭示了天窗风振的亥姆霍兹共振特性与声反馈机制。胡亚涛等[5]针对某比例车型，研究了天窗不同位置的速度剪切层变化，发现除了特征频率下的风振噪声，还存在较大频率范围的气动噪声。上述研究中，主要针对某个或某几个固定开度的车窗风振噪声进行研究，然而在实际应用中，这些研究方式对车窗开启的动态性模拟具有局限性。

为了降低车窗开启引起的风振噪声，国内外学者采取了一系列降噪措施。Kook等[6]采用主动导流板对某仓背式车型天窗部分开启时的风振噪声进行了控制，并且通过风洞试验验证该控制方法不受来流速度与侧风横摆角的影响。Rahman等[7]通过在某简易空腔上游附近另开一个小空腔降低了气流的不稳定性，缓解了气流冲击效应，进而降低了声压幅值与均方根值。周益[8]在保证汽车的气动外形下，改变天窗在车顶的位置，从而避免天窗共鸣区的位置，有效地降低了风振噪声。黄磊[9]通过在天窗附近安装网状挡风条，有效的降低了风振噪声强度，并通过风洞试验此方法在有侧风情况下也能获得良好的降噪效果。康宁等[10]对不同天窗尺度下的某轿车模型的风振噪声进行了数值模拟，获得了理想降噪效果下的合理天窗尺寸布置。

本文首先利用动网格技术对简易车厢连续滑移开口引起的风振噪声进行了数值模拟，在此基础上，对某轿车车型侧窗连续开启的风振噪声进行了仿真计算，计算结果与实车道路试验吻合良好，同时获得了风振噪声最大的侧窗开度，并分析了该开度下的风振机理与特性。最后建立左后侧窗非光滑表面雨挡，通过优化算法，确定了雨挡的结构参数，并取得了良好的降噪效果。

1 计算方法

1.1 湍流模型

采用大涡模拟(Large Eddy Simulation, LES)对风振噪声进行湍流环节的计算，该方法能够比传统的雷诺应力平均RANS(Reynolds-Areraged Navier Stokes)湍流模型取得更好的模拟效果。LES方程是通过对N-S方程进行波数或物理空间过滤而得到的一个大尺度运动方程，其形式为[11]

(1)

式中：ρ为流体密度;ui,uj为速度分量;μ为黏性系数;τij为亚格子尺度应力，体现了小尺度漩涡运动。

为使方程封闭，采用涡旋黏性亚格子模型(Sub-Grid Scale, SGS)，其形式为

(2)

式中：δij为克罗内克系数;μt为湍动能黏度。

1.2 动网格技术

当采用动网格技术进行CFD计算时，计算区域是变化的，所以要对上述流场控制方程进行修改，即考虑运动边界的影响，其形式可表示为[12]

(3)

式中：u为速度流量;ug为移动网格的移动速度;Γ为扩散系数;qφ为源项;V为控制体体积;Ω为控制体边界。

式(3)中时间导数项，可用一阶差分格式表示

(4)

式中：n和n+1为不同的时间层。n+1层上的Vn+1可以表示为

(5)

为了满足网格守恒律，控制体的时间导数可用下式进行计算

(6)

式中：ns为控制体积的面网格数;Aj为面j的面积向量。点乘可进一步表示为[13]

(7)

式中：δVj为控制面j在时间间隔Δt内扫过的空间体积。

汽车侧窗连续开启会带来流体域边界的刚性运动，从而引起数值模拟过程中的网格变形与较强的非定常效应，本文采用Fluent中的动网格技术来模拟该流动过程，开口或侧窗的运动规律由用户自定义函数(User Defined Functions, UDF)定义。

1.3 声学后处理

采用动网格技术对带有运动边界的流体区域进行CFD计算后，记录得到监测点脉动压力不同时刻点的数据，并截取稳定段数据进行FFT变换，得到脉动压力的幅值与频率的曲线，然后转化成以分贝为单位的声压级获得声压频谱，此过程可表示为

(8)

SPLm=20lg[pm(ω)/pref]

(9)

式中：pm(ω)为第m谐波幅值;参考声压pref为2×10-5Pa。

在整个计算过程中，运动边界在某状态下所对应的总声压级的获取是最重要的一步。根据每个谐波频率下的声压级，可得到在该状态下的计算频率范围内的总声压级(dB)[14]

P=OSPL=
10lg[10＾(0.1SPL1)+…+10＾(0.1SPLm)]

(10)

2 简易车厢算例验证

2.1 几何模型与网格划分

为了探究动网格计算方法在计算汽车风振噪声上的可行性，首先采用简易车厢模型作为参照，为了模拟车窗的连续开启，从而适用于动网格计算，对开口进行了处理。开口位于车厢正中央，尺寸为0.12 m×0.24 m×0.015 m，中间加一横板模拟汽车车窗，横板尺寸为0.118 m×0.24 m×0.008 m，为了满足网格连续性要求，初始开度为0.002 m,如图1(a)所示。

纵对称面上的网格示意图，如图1(b)所示。因为动网格对网格划分技巧要求高，在对网格进行划分时，添加了三处密度盒，最终的网格总数约为580万。

(a)计算域及简易车厢模型 (b)纵对称面上网格分布图1 CFD计算模型与网格划分Fig.1 Computational model and mesh generation of CFD

为了对动网格方法进行验证，建立了两个固定开度的简易车厢模型(带横板)进行固定开度仿真计算，横板开口开度分别为0.06 m,0.09 m,如图2和图3所示。

图2 固定开度为0.06 m的几何模型与网格划分Fig.2 Geometric model and mesh generation corresponding to the fixed opening degree of 0.06 m

图3 固定开度为0.09 m的几何模型与网格划分Fig.3 Geometric model and mesh generation corresponding to the fixed opening degree of 0.09 m

在进行动网格计算时，需要对不同的网格区域类型进行划分，以保证在边界运动时网格能够顺利更新，包括Stationary(静止区域)、Rigid Body(刚体运动区域)、Deforming(变形区域)。对简易车厢进行了动网格边界条件的划分，如图4所示。

图4 开口处动网格边界划分Fig.4 Dynamic boundary division near the opening

简易车窗模型总开度为0.12 m，来流速度为30 m/s，为了得到足够多的计数点，满足0.01 m的开度内，有1 000个数据点，则共需要12 000个数据点，瞬态迭代步数为12 000步，采样时间为2.4 s，时间步长为0.000 2 s，车窗开启速度为0.05 m/s。

2.2 验证对比

为了验证动网格仿真方法在进行风振噪声数值计算上的准确性，在动网格仿真连续计算完成后，分别提取出1.1～1.3 s,1.7～1.9 s各1 000个脉动压力值，近似模拟开度为0.06 m,0.09 m时的脉动压力时序变化，如图5所示。

运用近似等效替代法进行声学后处理，将得到的声压频谱曲线与固定开度仿真结果进行对比，对比结果如图6所示。

(a) 1.1～1.3 s (b) 1.7～1.9 s图5 监测点的脉动压力时序图Fig.5 Fluctuating pressure of monitoring point in time domain

(a)开度为0.06 m (b)开度为0.09m图6 测量点的脉动压力频谱图Fig.6 Sound pressure level of monitoring point

可以看出采用动网格仿真方法和固定开度仿真方法在低频范围内的计算结果上确实存在一些差异，这是因为在运用动网格方法计算时，网格更新需满足几何守恒律，每个网格单元的体积变化等于每个面在运动过程中扫过的体积之和，且网格面运动速度是通过中间点原则确定的，而在运用固定开度计算方法时，网格单元与节点的位置始终维持不变，无需满足几何守恒律。从图6(a)可知，当开度为0.06 m时，动网格方法计算得到的风振频率为134.2 Hz，声压级为101.26 dB；固定开度方法计算得到的风振频率为141.6 Hz，声压级为98.36 dB。从图6(b)可知，当开度为0.09 m时，动网格仿真方法计算得到的风振频率为129.8 Hz，声压级为104.63 dB；固定开度方法计算得到的风振频率为132.5 Hz，声压级为102.52 dB。依据Helmholtz共振原理，简易车厢的风振噪声频率预估公式为[15]

(11)

式中：c为声速;S为开口区域面积;T为空腔体积;h为横板厚度;Dh为开启区域的等效水力直径。

通过该公式可得到简易车厢开度为0.06 m与0.09 m时的风振噪声频率预估值为139 Hz与130 Hz，动网格仿真方法计算得到的基频值与预估值在合理偏差范围内，因此进一步证明了运用动网格仿真方法计算风振噪声是可行的。

3 实车算例验证与风振特性分析

3.1 动网格划分与求解器设置

实际的汽车是非常复杂的几何体，对风振噪声的计算与分析必须与实际车型相结合。图7为某轿车车身周围与内部的网格分布：车身表面几何参数梯度变化较小区域采用稀疏网格，梯度变化较大区域需对网格进行加密，车身附近使用密度盒进行局部加密；车身外表面采用三棱柱网格来计算流体黏性引起的附面层效应。

(a) (b)图7 车身外部与内部网格分布Fig.7 Grid distribution outside and inside the vehicle body

在进行瞬态计算之前，先进行稳态计算，并以此稳态计算得到的结果作为瞬态计算的初始值。稳态计算求解参数与边界条件设置可参照文献[16]，这里不再详细阐述。待稳态残差计算收敛后，以该稳态求解的结果作为动网格瞬态仿真计算的初始值。在瞬态计算的同时，模拟车窗的连续开启，连续开启是通过动网格实现的。采用弹簧近似光滑与局部重划模型相结合的方式来处理网格变形问题。一方面由于车窗附近区域使用的计算网格为非结构四面体网格，因此选取弹簧近似光滑模型；另一方面仿真计算的车窗开启运动的尺度较大，而局部重划模型能够很好地解决网格变形尺度大的问题，进而保证网格质量。

在Fluent软件中激活Dynamic Mesh选项，并同时打开Smoothing(弹簧光滑模型)和Re-meshing(局部重划模型)法。表1为Smoothing法的参数设置。

表2为Re-meshing法的参数设置。这些参数的含义主要用于确定哪些网格需要被重新划分。在缺省设置中，如果重新划分的网格优于原网格，则用新网格代替旧网格；否则将保持原网格划分不变。这些参数的设置依据是原始网格的畸变率和尺寸。

表1 Smoothing法的参数设置

表2 Re-meshing法的参数设置

表3为动网格边界条件参数设置，设置方法按照网格划分尺寸大小以及动网格车窗边界划分。

表3 动网格边界条件设置

实车模型的左后侧窗总开度为0.4 m，为了实车道路试验相吻合，在动网格仿真计算时，侧窗也仅开启4/5开度，即开启0.32 m，车速为30 m/s，为了满足声学后处理的需要，满足0.01 m的开度内，至少有1 000个数据点的要求，设计瞬态迭代步数为40 000步，共得到40 000个脉动压力信号，时间步长为0.000 2 s，采样时间为8 s，即车窗开启速度为0.04 m/s。

3.2 试验验证与对比

实车道路试验场地要求周围50 m范围内不能有其它噪声源的干扰，试验路面要求平直、平整、干燥且有足够长度，天气要求晴朗，无风或微风，背景噪声(A声级)应比被测车辆噪声至少低10 dB。为了减少环境噪声的干扰，试验路段为行车稀少时段且路面相对平直的某高速公路。传声器的布置严格依据GB/T 25982—2010。传声器布置与侧窗开度标识,如图8所示。

(a)传声器布置 (b)侧窗开度标识刻度图8 道路试验测试准备Fig.8 Road test of the vehicle

为了验证动网格计算方法运用在实车模型上的准确性，将左后窗1/5,2/5,3/5,4/5 4个开度的实验数据提取出来，与固定开度仿真结果、实车道路试验结果进行对比分析。

从图9中可知，无论是动网格计算结果还是固定开度计算结果在整个频率段均与实车道路试验结果有些差异，这是由于在实车道路试验中，不能完全避免其它噪声的干扰，而且数值仿真边界条件设置不能完全模拟实际情况。但是频谱曲线的走势基本一致，而且在风振噪声第一个峰值处吻合得比较好，风振噪声特征点的声压级和频率都相差不大，证明了仿真方法的准确性。动网格计算结果和固定开度计算结果在低频段吻合较好，尤其在风振噪声特征点处误差很小，但在中高频差异有所增大。当侧窗开度增加至3/5时，高频的连续开度仿真值与试验值偏差更为明显，这是因为开度的增加会引起风振频率的增加，当风振频率接近声腔的固有频率时，引起声共振，使得压力脉动的准谐振效应更为显著，进而使高频声压值的误差被放大。当车窗开度增加至4/5时，风振频率已经越过声腔的固有频率，使得高频声压值的误差值有所降低。

(a)1/5开度 (b)2/5开度 (c)3/5开度 (d)4/5开度图9 声压频谱图对比(110 km/h)Fig.9 Comparison of sound pressure level under different opening degrees in frequency domain (110 km/h)

3.3 最大风振特性分析

根据式(10)可求出不同侧窗开度下所对应的总声压级，如图10所示。从图10可知，风振噪声总声压级随着侧窗开度的增大先增加后减小，当侧窗开启至70%附近时，该开度对应的风振频率接近乘员室声腔的固有频率，因此在计算频率范围内，总声压级达到最大值。总体而言，运用固定开度方法与动网格仿真方法所得结果与试验结果趋势较为一致，吻合良好，因此最大风振噪声声压值与其对应的侧窗开度均取三者结果的平均值，即开度为69%，峰值为129 dB。

依据以上计算与分析，左后侧窗开度为276 mm时，风振噪声声压级达到最大值，因此对该工况进行风振特性分析。图11中由于气流直接从左后侧窗进入车内，同时B柱后涡流以及后视镜产生的尾涡在侧窗开口处相遇，车厢中后部气流流速较高，形成了很多较大的漩涡。由于气流在车内回旋流向车厢前部时，产生了涡系，引起流速与流量的增加，进而对风振噪声产生了直接的影响。图12为横截面上的湍动能云图，气流流经后视镜时，在其后部附近形成强烈的湍流，经过一段距离的发展，到达左后侧窗附近时，湍流部分能量随之耗散，湍流强度也相应减弱，部分湍流转化为层流，因此对侧窗风振噪声有直接影响。

图10 总声压级对比图Fig.10 Comparison of overall sound pressure level under different opening degrees

图11 横切面速度云图(单位：m/s)Fig.11 Velocity contour of the cross section (unit: m/s)

图12 横切面湍动能云图(单位：K)Fig.12 Turbulence energy contour of the cross section (unit: K)

4 侧窗风振噪声控制

仿生学的研究发现，生长在我国东北地区的长耳鸮，喜欢夜间行动，飞行时悄无声息，研究学者发现长耳鸮翼后缘是柔性非光滑表面，具有降噪作用[17]。 本文将左后窗雨挡形状设计成非光滑表面，既能具备传统雨挡的功用，又能起到扰流作用，达到降噪目的，对其在侧窗风振噪声方面的影响进行了研究，并针对其外形进行了优化设计。

4.1 雨挡模型设计变量及约束条件

本文在对实车雨挡测量后，对雨挡某些对影响气流流动很小的部位进行了简化，建立非光滑表面雨挡模型,如图13所示。在光滑雨挡表面，以正弦曲线生成四道凹凸不平的槽。

(a) (b)图13 雨挡装置主要结构参数Fig.13 Main structural parameters of the rain guard

根据非光滑表面雨挡的形状及造型特征，选取如下参数作为设计变量：

L1-取非光滑表面每个单元中线之间的间距，则L1的取值范围为20～26 mm。

W-令雨挡下缘与车窗曲面距离为W，则变换W值可以控制降噪附加装置表面的斜度。当降噪附加装置表面斜度大于45°时，挡雨效果会急剧下降，令W最小值为20 mm，因此W取值范围为20～36 mm。

L2-令雨挡长边(即后部边长)的长度为L2，根据车窗弧度要求，令L2的最小值为50，取L2的范围为50～65 mm。

H-取非光滑单元的凸起高度，根据仿生学可知H/L取0.12～0.19，H取值范围为3～5 mm。

非光滑表面雨挡会影响车窗开口前缘剪切层产生的涡流，因此选取驾驶员耳旁处的风振噪声值作为目标函数。

4.2 试验设计与代理模型

根据设计变量的取值范围，选取的设计变量共4个，采用最优拉丁超立方抽样方法设计了20组样本点，经CFD计算得到20组响应值，设计的具体方案,如表4所示。

图14为设计变量对车内噪声值P的主效应图。主效应图表示的是改变某单因子的水平，用每个水平和其他因子的所有可能的组合对结果进行平均。从图中不同曲线的斜率可以看出，车内风振噪声P随L1和W的增大而不断减小，L1的斜率大于W的斜率，即P随L1的变化更为显著。同时，随着H和L2增大，P先增大后减小。

图15为风振噪声的Pareto图，对风振噪声值P影响由大到小依次是L1,W,H和L2。其中，L1和W为负效应，H和L2为正效应。

表4 试验设计方案样本

图14 主效应图 图15 Pareto图Fig.14 Main effect plotFig.15 Pareto plot

基于表4中优化目标与设计变量之间的响应性关系，选取设计空间范围中除设计方案以外的任意2组样本点，进行CFD计算，最后将得出的计算结果同近似模型的结果进行对比，以此来验证近似模型精度[18]，如表5所示。结果表明近似模型与仿真值误差都在2%以内，近似模型能够高精度地描述响应值和设计变量之间关系。

表5 近似模型精度验证

4.3 优化结果与分析

遗传算法是借鉴达尔文进化论的进化规律演化而来的一种全局搜索优化算法，可同时使用多个搜索点的信息，目前广泛应用于工程优化领域。多岛遗传算法是一种基于群体分组的并行性遗传算法，这种算法通过若干子群的独立进化与相互迁移避免了传统算法可能产生的局部最优解现象，有利于寻找到全局最优解，同时计算效率高并且算法稳定性好[19]。本次优化目的是降低风振噪声值，即MinimizeP。

在近似代理模型基础上，应用多岛遗传算法进行全局寻优设计，子群规模设定为20，总群体规模数为50，总进化代数为20代，对代理模型进行全局寻优，得到结果为：L1=21.20 mm，W=25.39 mm，L2=63.29 mm，H=4.31 mm。

将得到的最优解进行CFD计算验证，对比图16与图11可知，车内气流的流速明显减小，且漩涡大小和数量都有所减少，因此导致驾驶员耳旁声压级有所降低；对比图17与图12可知，附加上结构优化的雨挡后，使得左后窗附近的一部分层流转化成湍流边界层，间接削弱了空腔风振声学响应强度[20]，因此附加后的雨挡装置对风振噪声起了一定的抑制作用。

优化后风振噪声为123.82 dB，相较无降噪附加装置的129 dB，降低了约5 dB，减小约4%，降噪效果较为理想，如表6所示。

图16 横切面速度云图(加雨挡)Fig.16 Velocity contour of the cross section (additional rain guard)

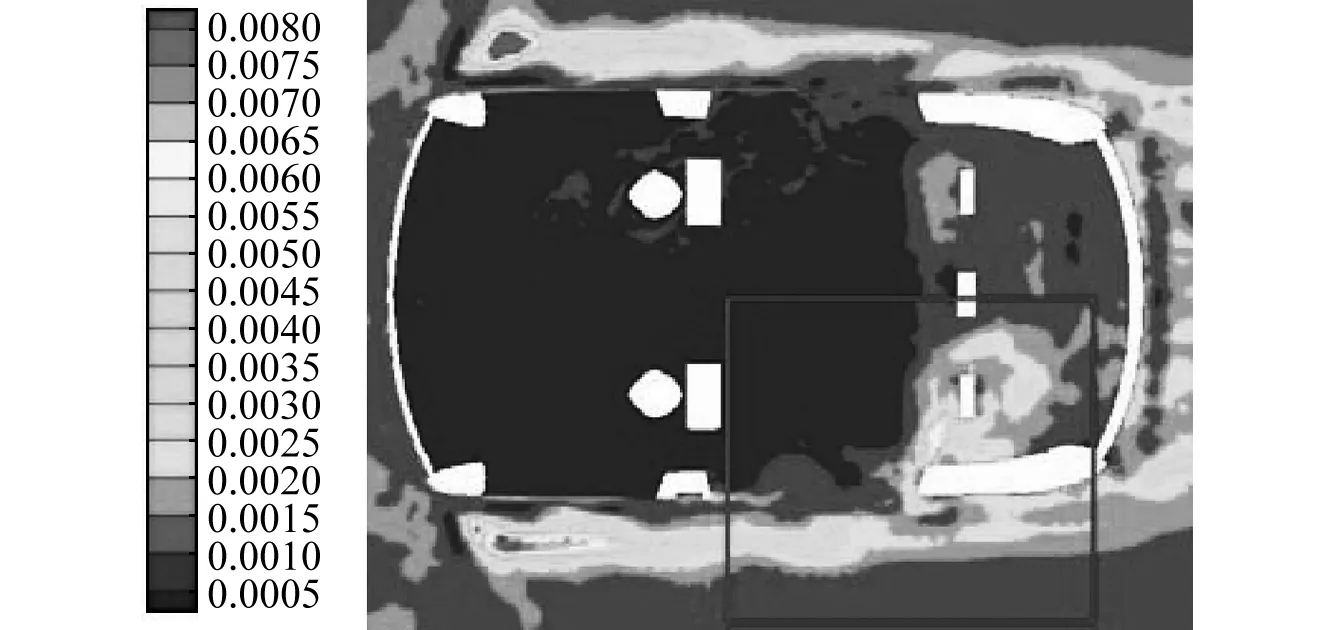
图17 横切面湍动能云图(加雨挡)Fig.17 Turbulence energy contour of the cross section (rain guard)

无雨挡结构优化后的雨挡近似模型CFD计算相对误差改进效果129 dB123.36 dB123.82 dB0.37%4.18%

5 结 论

(1)采用非结构网格弹性变形与局部重构网格相结合方法实现了简易车厢的连续开口风振噪声计算。通过与传统固定开度方法对比分析，验证了运用该方法计算空腔风振噪声的准确性。

(2)在对简易车厢连续开口风振噪声准确计算基础上，采用动网格技术对实车左后窗连续开启的风振噪声进行了数值仿真。虽然该方法计算结果与传统计算结果、试验结果在高频部分有较大差异，但是对于风振特征点对应的频率及幅值吻合的比较好，进而找到风振噪声最大值所对应的车窗开度，为不同车窗开度下的风振噪声预测与避开噪声值较大的车窗开度提供了新的实际应用模型与新的研究思路。

(3)通过在左后窗附近建立非光滑表面雨挡，并对其主要结构参数进行优化设计，附加优化后的雨挡装置削减与削弱了向前排座椅回流涡的数量与流速，并将左后窗表面附近部分层流转为湍流，影响了该区域的湍流强度，降低了驾驶员耳旁的风振声压级，为雨挡装置在汽车侧窗风振噪声控制领域中的应用提供了一定程度的工程指导。

参 考 文 献

[ 1 ] 傅立敏. 汽车设计与空气动力学[M]. 北京： 机械工业出版社， 2011.

[ 2 ] LEMAITRE G, VARTANIAN C, LAMBOURG C, et al. A psychoacoustical study of wind buffeting noise[J]. Applied Acoustics, 2015, 95: 1-12.

[ 3 ] MENDONCA F G. CFD/CAE combination in open cavity noise predictions for real vehicle sunroof buffeting[J]. SAE International Journal of Passenger Cars-Mechanical Systems, 2013, 6(1): 360-368.

[ 4 ] 杨振东，谷正气，董光平，等. 汽车天窗风振噪声分析与优化控制[J]. 振动与冲击, 2014, 33(21): 193-201.

YANG Zhendong, GU Zhengqi, DONG Guangping, et al. Analysis and optimal control for car sunroof buffeting noise[J]. Journal of Vibration and Shock, 2014, 33(21): 193-201.

[ 5 ] 胡亚涛，薛永飞，陈军，等. 车辆天窗气动噪声的数值分析与实验研究[J]. 工程热物理学报, 2011, 32(4): 589-892.

HU Yatao, XUE Yongfei, CHEN Jun, et al. Numerical simulation and experimental study of vehicle aerodynamic noise from open sunroof[J]. Journal of Engineering Thermophysics, 2011, 32(4): 589-592.

[ 6 ] KOOK H S, SHIN S R, CHO J, et al. Development of an active deflector system for sunroof buffeting noise control[J]. Journal of Vibration and Control, 2014, 20(16): 2521-2529.

[ 7 ] RAHMAN M M, TOUFIQUE H A B M, SADRUL I A K M, et al. Computation of transonic internal flow around a biconvex airfoil with cavity[J]. Journal of Mechanical Science and Technology, 2015, 29(6): 2415-2421.

[ 8 ] 周益. 汽车天窗噪声的控制和CFD仿真研究[D]. 合肥: 合肥工业大学, 2012.

[ 9 ] 黄磊. 汽车天窗风振问题的研究[J]. 噪声与振动控制, 2009, 29(2): 38-41.

HUANG Lei. Study of sunroof buffeting noise of automobiles due to wind load[J]. Noise and Vibration Control, 2009, 29(2): 38-41.

[10] 康宁，王晓春. 天窗对轿车内部流场及气动噪声的影响[J]. 航空动力学报, 2010, 25(2): 354-358.

KANG Ning, WANG Xiaochun. Influence of sunroof on flow field and aerodynamic noise inside the passenger compartment of the car[J]. Journal of Aerospace Power, 2010, 25(2): 354-358.

[11] 汪怡平，王文龙，杨雪，等. 超低马赫数空腔流诱发自激振荡数值模拟[J]. 中国公路学报, 2015, 28(7): 121-126.

WANG Yiping, WANG Wenlong, YANG Xue, et al. Numerical simulation for self-oscillation evoked by cavity flow at ultra low mach numbers[J]. China Journal of Highway and Transport, 2015, 28(7): 121-126.

[12] 熊万里，侯志泉，吕浪，等. 基于动网格模型的液体动静压轴承刚度阻尼计算方法[J]. 机械工程学报, 2012, 48(23): 118-126.

XIONG Wanli, HOU Zhiquan, LÜ Lang, et al. Method for calculating stiffness and damping coefficients of hybrid bearings based on dynamic mesh model[J]. Journal of Mechanical Engineering, 2012, 48(23): 118-126.

[13] 艾辉林，陈艾荣. 基于ALE格式的动网格方法数值模拟断面气动导数[J]. 工程力学, 2009, 26(7): 211-215.

AI Huilin, CHEN Airong. Moving grids method simulation of sections’ aerodynamic derivatives based on ALE format[J]. Engineering Mechanics, 2009, 26(7): 211-215.

[14] 黄莎，杨明智，李志伟，等. 高速列车转向架部位气动噪声数值模拟及降噪研究[J]. 中南大学学报(自然科学版), 2011, 42(12): 3899-3904.

HUANG Sha, YANG Mingzhi, LI Zhiwei, et al. Aerodynamic noise numerical simulation and noise reduction of high speed train bogie section[J]. Journal of Central South University(Science and Technology), 2011, 42(12): 3899-3904.

[15] MECHEL F P. Formulas of acoustics[M]. Berlin: Springer-Verlag Press, 2008.

[16] 朱晖，杨志刚，谭鹏，等. 流体仿真平台对汽车外流场仿真能力的对比研究[J]. 汽车工程, 2016, 38(2): 163-167.

ZHU Hui, YANG Zhigang, TAN Peng, et al. A comparative study on the simulation capability of fluid simulation platforms on exterior flow field around vehicle[J]. Automotive Engineering, 2016, 38(2): 163-167.

[17] 徐成宇，钱志辉，刘庆萍，等. 基于长耳鸮翼前缘的仿生耦合翼型气动特性[J]. 吉林大学学报(工学版), 2010, 40(1): 108-112.

XU Chengyu, QIAN Zhihui, LIU Qingping, et al. Aerodynamic performance of bionic coupled foils based on leading edge of long-eared owl wing[J]. Journal of Jilin University (Engineering and Technology), 2010, 40(1): 108-112.

[18] 左曙光，韦开君，吴旭东，等. 采用Kriging模型的离心压缩机叶轮多目标参数优化[J]. 农业工程学报, 2016, 32(2): 77-83.

ZUO Shuguang, WEI Kaijun, WU Xudong, et al. Multi-objective parameter optimization of centrifugal compressor impeller with Kriging model[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(2): 77-83.

[19] 赵德建，王延奎，周平，等. 基于多岛遗传算法的二维翼型吸气减阻优化[J]. 北京航空航天大学学报(自然科学版), 2015, 41(5): 941-946.

ZHAO Dejian, WANG Yankui, ZHOU Ping, et al. Optimization of drag reduction by suction using multi-island genetic algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics(Science and Technology), 2015, 41(5): 941-946.

[20] 杨博. 汽车外部空气动力噪声研究[D]. 长春: 吉林大学, 2008.