实模态跳跃现象的原因及影响分析
张 淼, 于 澜, 鞠 伟
(1. 长春工程学院 理学院,长春 130012; 2. 中国第一汽车股份有限公司 技术中心,长春 130011)
许多工程结构往往会由于自身外界因素的影响,在结构参数发生微小的变化时,引起结构的部分模态出现急剧变化的现象,称之为模态跳跃现象。这种现象最早是美国国家航天局的专家在弹性薄板构件的瞬态屈曲试验过程中发现的,随后一些学者作了后续的研究[1-2],近年来,这种现象在力学及工程领域逐渐得到关注,而研究对象也由柔性板等简单构件逐渐向更复杂的结构转变[3-4]。此外,在对密频系统与重频系统的研究过程中[5-6],研究人员发现频率密集极可能会引起模态跳跃现象的发生[7-8],但这种现象的产生原因及其对结构产生的影响目前还未被提及。
结构的固有频率(实频率)及固有振型(实模态)信息是获得其精确响应的基础[9-10],它们的变化对振动分析与控制的影响一直是人们关注的问题,它们的灵敏度值是度量其变化的重要手段。灵敏度分析可以从数值角度去分析实模态和实频率发生变化的位置及程度。同时,根据本文的研究可知,灵敏度分析还可以解释模态发生跳跃的原因。
对于一个复杂阻尼系统,首先在设计参数的可行域内采样实频率和实模态的数据,利用三次样条插值绘制它们关于设计参数的曲线图。通过实频率曲线图可以发现密频区间,重频点及弯转区间等。通过实模态曲线图可以发现模态跳跃、对换及尖峭等现象和变化特点,并找出频率变化与模态变化之间的内在联系。其次利用全模态算法计算设计参数观察点处所对应的系统模态的一阶灵敏度,从而揭示模态变化的原因,并把数值计算结果与几何曲线分析的结果进行对照,以利于准确而全面地反映系统模态参数变化的规律。最后针对在设计参数的观察点处所构成的多种密频、重频、接近密频和接近重频等实际结构系统,利用实模态和实频率来计算其稳态响应,同样使用三次样条插值来获得响应曲线,从而对比分析模态跳跃现象对振动分析的影响,以满足对各种系统的结构优化及控制的需要。
1 基本理论
N自由度的线性离散振动系统的运动方程为
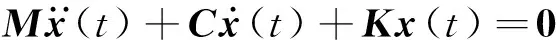
(1)

(2)
设每个实模态的正则(或称规范化)常数为ai, 即
(3)

(K-λiM)φi=0
(4)
实际上特征矩阵方程式(4)是关于矩阵M和K的广义特征问题。 设Φ=[φ1,φ2,…,φN]为无阻尼正则实模态矩阵(下文中在不引起歧义的情况下,正则实模态仍简称为实模态),对单频对称系统而言,实模态关于矩阵M和K是加权正交的。因此
再由式(3),可得
即
ΦTMΦ=E
(5)
代入式(4),可得
ΦTKΦ=diag(λ1,λ2,…,λN)
(6)
引入设计参数向量b=(b1,b2,…,bq)T, 相应地特征矩阵方程式(4)应为K(b)φ(b)-λ(b)M(b)φ(b)=0,为了讨论方便,以下我们仍简记为式(4)的形式。
(7)

将式(4)两边对第j个参数bj求导,得
K,jφi+Kφi,j=λi,jMφi+λiM,jφi+λiMφi,j
(8)

整理式(8)得实模态一阶灵敏度φi,j的支配方程为
(K-λiM)φi,j=(λi,jM-K,j+λiM,j)φi
将式(7)代入支配方程,并左乘ΦT, 得
ΦT(K-λiM)Φa(ij)=ΦT(λi,jM-K,j+λiM,j)φi
用单频系统实模态向量之间的规范正交化关系式(5)和式(6)解耦支配方程,即可析出一阶灵敏度系数的控制方程为
由第i个以外的方程可解得一阶灵敏度系数为


(9)


(10)
由式(9)和式(10)即获得全部一阶灵敏度系数,代入式(7)即可获得第阶实模态的一阶灵敏度为

(11)
需要说明的是,上文中的实模态的一阶灵敏度算法对重频完备系统中的单频所对应的实模态也是适用的(完备系统指的是N维特征空间中可以找到N个无关的特征向量作为基底),但不适用于重频所对应的实模态的一阶灵敏度分析。
一阶灵敏度可以反映实模态对结构的某些参数所产生扰动的敏感程度,灵敏度越高说明模态越不稳定,因此上述灵敏度的计算公式可以用于测量结构模态的跳跃程度。
由式(11)可知,由于该式右端第二项的分母中含有因子(λk-λi),而当所求模态落入模态密集区时,它们所对应的频率差越小,其一阶灵敏度系数就会相对越大,因此所求模态的一阶灵敏度就会较大,这会导致所求模态产生跳跃。换句话说,模态的密集区间所包含的模态越多,模态们的跳跃性就会越踊跃。另外式(11)还说明,所求模态的一阶灵敏度是由所有模态的线性组合来表示的,因此那些灵敏度系数不为零的模态的取值也会影响所求模态的一阶灵敏度的大小。再由于式(11)中还含有M,j和K,j,所以这些结构性质矩阵关于设计参数的灵敏度也是影响所求模态的一阶灵敏度的大小的因素之一。
综上所述,实模态的跳跃性的影响因素有三个:①实频率的密集程度; ②实模态的取值;③结构性质矩阵的灵敏度。但是由式(11)可以排除实频率的弯转对实模态跳跃性的影响。这是因为实频率的弯转就会导致它的灵敏度发生变化,而在式(11)中不含有实频率的灵敏度。
2 数值算例1
2.1 实模态跳跃现象
考虑一个2自由度的阻尼系统,如图1所示。
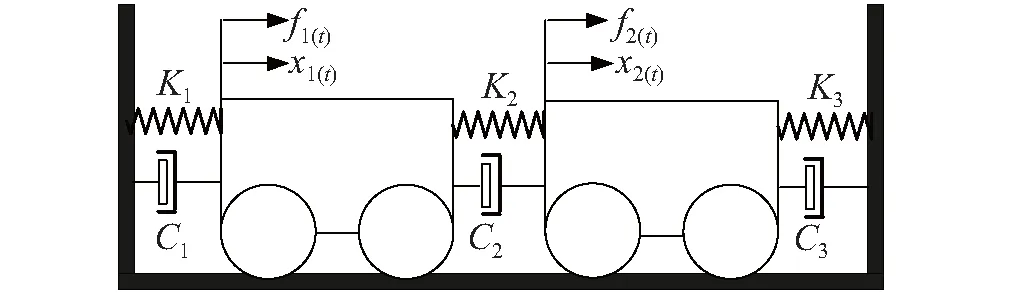
图1 两自由度阻尼振动系统Fig.1 A two-degree-of-freedom system
其中,质量、刚度和阻尼矩阵分别为
为了得到实频率的曲线图,需进行采样。特征矩阵方程式(4)是个广义特征问题,化为一般特征问题为
λiφi=M-1Kφi
(12)
转化为矩阵M-1K的标准特征问题, 其中φi={φi1φi2}T(i=1,2)是经过式(3)规范化后的实模态。 令m1=m2=1,k2=0.005,k3=1,取设计参数为k1, 在k1的变化区间[0.6,1.4]内以0.1为步长间隔,按式(12)采样实频率数据,再用三次样条插值,得到实频率λ1与λ2关于设计参数k1的拟合曲线图,如图2所示。

图2 实频率关于设计参数k1的曲线Fig.2 Real frequencies versus k1
由图2可知,系统在k1=1处发生两个特征值λ1与λ2接近的现象,也就是说,当m1=m2=1,k1=1,k2=0.005,k3=1时系统成为一个实频率密集系统,简称为密频系统。那么k1取[0.6,1.4]内除1以外的其它值时所形成的系统均称为接近密频系统。
与实频率的分析过程类似,令m1=m2=1,k3=1,k2=0.005, 而取设计参数为k1,其变化区间取为0.6~1.4, 以0.1为步长间隔,获取由式(5)和式(12)得到的φ1和φ2关于设计参数k1的拟合曲线图,如图3和图4所示。

图3 第1阶实模态φ1关于设计参数k1的曲线Fig.3 The first real mode versus k1
由图3和图4可知,φ1和φ2均在k1=1处两侧发生了急转和跳跃。因此这里确定了实模态跳跃现象是存在的。

图4 第2阶实模态φ2关于设计参数k1的曲线Fig.4 The second real mode versus k1
2.2 实模态跳跃现象的原因分析
当k1=1时,通过计算可得此密频结构的两个实模态为
φ1=(-0.707 1,-0.707 1)T
φ2=(-0.707 1,0.707 1)T
两个实频率为λ1=1,λ2=1.01。 由式(7)可知
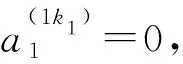

因此,由式(11)得
根据上面的计算过程可知,模态的密集、模态的取值及结构性质矩阵的灵敏度确实是影响实模态跳跃性的重要因素。再由计算结果可知,第1阶实模态的第1维分量在k1=1处的灵敏度为正值,它在此处附近必然单调增加且幅度剧烈,其第2维分量在k1=1处的灵敏度为负值,它在此处附近必然单调减少且幅度剧烈,据此数值结果分析第1阶实模态必然在k1=1处发生了跳跃。
这个数值结果分析与图3所见事实相符。类似地可以分析第2阶实模态的跳跃现象及原因。
2.3 实模态跳跃现象对振动分析影响


图5 k1=1时的密频系统的响应Fig.5 Response of closed-frequency system at k1=1

图6 k1=0.8时的接近密频系统的响应Fig.6 Response of quasi-closed-frequency system at k1=0.8

图7 k1=1.2时的接近密频系统的响应Fig.7 Response of quasi-closed-frequency system at k1=1.2
由图3和图4及本文“2.2”中的分析可知,只有设计参数k1在密频点1处时,相应的密频系统的实模态灵敏度最大,即模态的跳跃性最强,但通过图5、图6和图7的对比分析可知,最密频系统的响应幅度与接近密频系统的响应幅度相比并无显著变化,这也说明密频系统的响应是稳定的。
3 数值算例2
3.1 实模态跳跃现象
考虑一个具有非比例阻尼的3自度阻尼振动系统,如图8所示。

图8 三自由度转子的动力模型Fig.8 A three-degree-of-freedom rotor dynamic model
其质量、阻尼和刚度矩阵分别为
令m1=1 kg,m2=1 kg,m3=1 kg,k1=k5=1 000 N/m,k2=k3=0 N/m,c1=c2=c3=10 N/(m·s-1),c=0 N/(m·s-1)。取设计参数为k4,在k4的变化区间[970,1 050]内以10为步长间隔,按式(12)采样实频率,再用三次样条插值,得到实频率λ1,λ2和λ3关于设计参数k4的拟合曲线图,如图9所示。
由于图9中有重叠的部分,因此给出实频率的数据,更进一步地反映实频率的状态,见表1。
由图9和表1可知,当k4=1 000时,系统的三个实频率全都发生了重复,称其为具有3重频率系统,而
k4在[970,1 050]内取除1 000外的其它值时所形成的系统称为具有2重频率系统。用与实频率分析类似的方法,即用式(5)和式(12)采样并插值获取实模态φ1,φ2和φ3关于设计参数k4的拟合曲线,如图10、图11和图12所示。

图9 实频率关于设计参数k4的曲线Fig.9 Real frequencies versus k4

参数数值k49809901 0001 0101 0201 0301 040λ19809901 0001 0001 0001 0001 000λ21 0001 0001 0001 0001 0001 0001 000λ31 0001 0001 0001 0101 0201 0301 040

图10 第1阶实模态φ1关于设计参数k4的曲线Fig.10 The first real mode versus k4

图11 第2阶实模态φ2关于设计参数k4的曲线Fig.11 The second real mode versus k4

图12 第3阶实模态φ3关于设计参数k4的曲线Fig.12 The third real mode versus k4
由图10和图12可知,φ1和φ3均在k4=1 000附近发生了急转和跳跃,而在其它点处相对稳定。在图11中显示,无论设计参数k4如何变化φ2都保持了绝对的稳定。与上一个算例一样,我们同样证实了实模态跳跃现象是存在的。
3.2 实模态跳跃现象的原因分析
从图10可知,第1阶实模态在设计参数k4从990~1 000的过程中,发生了跳跃。而跳跃现象发生的具体位置不能在图中得以确定,在不加密采样节点的情况下,下面从数值角度来确定模态发生跳跃的位置,并分析模态跳跃的原因。
首先当k4=990时,通过计算可得此具有2重频率系统的三个实模态为φ1=(0,0,1)T,φ2=(0,1,0)T,φ3=(1,0,0)T, 三个实频率为λ1=990,λ2=1 000,λ3=1 000,且它的三个实模态φ1,φ2和φ3是线性无关的,这说明系统是一个完备的具有2重频率系统,其第1阶实模态的灵敏度可以通过本文的方法求解。由式(7)可知
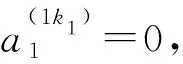
最后由式(11)得
φ1,k4=0
由于这是一个疑似发生跳跃的位置,为了验证计算的灵敏度的正确性,考虑再用差分灵敏度作进一步的分析。分别取设计参数的扰动量为Δk4=±0.01, Δk4=±0.001, Δk4=±0.000 1, Δk4=±0.000 01时分别计算系统的第1阶实模态的左侧和右侧的一阶差分灵敏度,其结果均为0。因此计算灵敏度φ1,k4=0的结论是正确的,第1阶实模态在此点附近相对稳定,并没有发生跳跃。
再继续寻找跳跃位置。在k4=1 000时这个系统的三个实频率均相同,所以通过计算可得此时系统的三个实模态分别为φ1=(1,0,0)T,φ2=(0,1,0)T,φ3=(0,0,1)T显然它们是线性无关的,因此这是一个重频完备系统。由于所求的第1阶实模态是重频所对应的模态,现考虑用差分方法来估计第1阶模态的一阶灵敏度。分别取设计参数的扰动量为Δk4=±0.01, Δk4=±0.001, Δk4=±0.000 1时分别计算系统的第1阶实模态的一阶左侧及右侧差分灵敏度,数值结果见表2。
由表2的数据说明第1阶实模态φ1在点k4=1 000处是不可导的,这当然会导致φ1在k4=1 000处发生跳跃。类似地可分析得到第3阶实模态在点k4=1 000处是不可导的,但第2阶实模态在点k4=1 000处的计算灵敏度与差分灵敏度均为0。以上数值分析结果与图10、图11和图12所示的事实相符。

表2 第1阶实模态在k4=1 000处的差分灵敏度计算结果
通过以上分析可说明,对实频率重复系统来说,因为模态可能存在不可导现象,因此它们极可能会发生跳跃。
3.3 实模态跳跃现象对振动分析影响


图13 k4=1 000时的重频系统响应Fig.13 Response of multi-frequency system at k4=1 000

图14 k4=970时的接近重频系统的响应Fig.14 Response of quasi-multi-frequency system at k4=970

图15 k4=1 020时的接近重频系统的响应Fig.15 Response of quasi-multi-frequency system at k4=1 020
由图10、图11和图12及本文“3.2”中的分析可知,结构实模态在k4=1 000时跳跃性最强,但由图13、图14和图15对比分析可知,实模态的跳跃性对振动分析的影响并不大。
4 结 论
本文针对由设计参数变化所产生的实频率密集及实频率重复等系统,展示了实模态可能发生的跳跃现象,并利用模态的一阶灵敏度分析了这种跳跃产生的原因。然后在对这些系统施加相同的简谐激励后,分析模态跳跃性对其稳态响应所产生的影响,可得到如下结论:
(1) 实模态在其不可导处会发生跳跃现象。
(2) 实频率的密集会导致跳跃现象的发生,且密频程度越高时,模态的跳跃性越强。
(3) 实频率的弯转并不是直接导致模态灵敏度变化的明显因素。
(4) 结构的性质矩阵的灵敏度及实模态的取值也是影响模态变化的不可忽视的原因。
(5) 虽然某些重频系统的模态跳跃性最强,但这种现象对它的振动响应的影响并不大。
(6) 虽然某些最密频系统的模态跳跃性最强,但是最密频系统的响应与其它接近密频系统的响应相比振幅却是最小的。
参 考 文 献
[ 1 ] EDUARD R,CHARLE C R,FRANCIS A B. On the solution of mode jumping phenomena in thin-walled shell structures[J]. Computer Methods in Applied Mechanics and Engineering, 1996,136(1/2): 59-92.
[ 2 ] EVERALL P R,HUNT G W. Mode jumping in the buckling of struts and plates: a comparative study[J]. International Journal of Non-Linear Mechanics, 2000,35(6): 1067-1079.
[ 3 ] 于岩磊,高维成,刘伟,等. 密集模态结构模态跃迁分析的简化摄动法[J]. 工程力学,2012, 29(3): 33-39.
YU Yanlei, GAO Weicheng, LIU Wei, et al. Simplified perturbation mehtod for analyzing the mode jumping of closed mode structure [J]. Engineering Mechanics, 2012, 29(3): 33-39.
[ 4 ] 蒋友宝,冯健,孟少平. 结构损伤识别中模态跃迁的研究[J]. 工程力学,2006, 23(6): 35-40.
JIANG Youbao, FENG Jian, MENG Shaoping. Mode jumping research in structural damage identification[J]. Engineering Mechanics, 2006, 23 (6): 35-40.
[ 5 ] 张淼,于澜,鞠伟. 重频结构模态灵敏度分析的高精度截模态算法[J]. 振动工程学报,2014, 27(4): 526-532.
ZHANG Miao, YU Lan, JU Wei. A high accuracy truncated modal algorithm of sensitivity analysis for multiple-frequency structure[J]. Journal of Vibration Engineering, 2014, 27(4): 526-532.
[ 6 ] 张淼,于澜,鞠伟. 模态跳跃现象对振动分析的影响研究[J]. 合肥工业大学学报(自然科学版),2015, 38(11): 1524-1529.
ZHANG Miao, YU Lan, JU Wei. Reserch on the effect of modal jumping phenomenon on vibration analysis[J]. Journal of Hefei University of Technology (Nature Secience), 2015, 38(11): 1524-1529.
[ 7 ] 刘潇翔,胡军. 包含密集模态的空间结构的模糊主动振动控制[J]. 空间控制技术与应用, 2010,36(4): 18-24.
LIU Xiaoxiang, HU Jun. Fuzzy vibration control of space structures with close modes[J]. Aerospace Control and Application, 2010,36(4): 18-24.
[ 8 ] 刘利军,樊江玲,张志谊,等. 密频系统模态参数辩识及其振动控制的研究进展[J]. 振动与冲击,2007, 26(4): 109-115.
LIU Lijun, FAN Jiangling, ZHANG Zhiyi, et al. Study progresses in modal parameters identification and vibration control of systems with crowded modes[J]. Journal of Vibration and Shock, 2007, 26(4): 109-115.
[ 9 ] 谭平,卜国雄,刘红军,等. 带TMD结构的随机地震响应分析的新方法[J]. 北京理工大学学报,2010,30(4): 390-394.
TAN Ping, BU Guoxiong, LIU Hongjun, et al. A new method for the random earthquake response analysis of the TMD-Structure[J]. Transactions of Beijng Institute of Technology, 2010,30(4): 390-394.
[10] 陈臻林. 大型结构动力响应的状态方程的Krylov精细时程积分法[J]. 力学与实践,2010, 32(2): 76-81.
CHEN Zhenlin. Krylov precise time-step integration algorithm for large-scale structure dynamic equations[J]. Mechanics in Engineering, 2010, 32(2): 76-81.
[11] 张淼,于澜,鞠伟. 基于频响函数矩阵计算阻尼系统动力响应的新方法[J]. 振动与冲击,2014,33(4): 161-166.
ZHANG Miao, YU Lan, JU Wei. A new method for computing dynamic response of a damped linear system based on frequency response function matrix[J]. Journal of Vibration and Shock , 2014,33(4): 161-166.

