考虑应变依赖性的硬涂层圆柱壳振动特性有限元分析

张 月， 孙 伟

(东北大学 机械工程与自动化学院，沈阳 110819)

圆柱壳作为工程中最常见的一类构件，尤其在航空和航天领域被大量使用。在服役过程中，圆柱壳经常因遭受宽频激励而引发共振，进而造成性能恶化或者疲劳失效。因而，需要研发相应的阻尼减振措施以抑制圆柱壳的有害振动。目前，通过在表面贴敷黏弹性阻尼层[1-3]成为圆柱壳减振的重要技术手段。但是，对于需要在高温及高腐蚀环境下工作的圆柱壳，例如航空发动机机匣、鼓筒等，上述黏弹性阻尼减振技术通常难以使用。硬涂层是由金属基、陶瓷基或者两者混合制成的涂层材料。最近的研究[4-6]发现其在高温、高腐蚀环境下可实现对薄壳结构过大的振动进行控制，由此可见，可以将硬涂层减振技术应用到圆柱壳振动控制上。为此，需要开展硬涂层圆柱壳的动力学建模与振动预估的研究。

硬涂层材料具有应变依赖性[7-8]，其力学特性参数会随着应变响应幅度的变化而改变。这种材料非线性使创建硬涂层圆柱壳动力学模型成为一项具有挑战性的任务。目前，考虑硬涂层材料的非线性特点，针对梁[9]及板[10]已有了一些初步研究。另外，学者们对黏弹性阻尼复合圆柱壳的动力学建模也开展了大量研究，Zheng等[11]用传递函数法分析了具有被动约束阻尼层的圆柱壳的振动特性。李晓妮等[12]也用传递矩阵法分析了具有主动约束阻尼层圆柱壳的振动特性。Jin等[13]用修正的Fourier-Ritz法推导了具有约束阻尼圆柱壳的运动方程并对复合壳的阻尼及振动特性进行了预估。以上这些都可为本文硬涂层圆柱壳动力学建模提供参考。

有限元法是一种强有力的建模方法，Li等[14]应用迭代有限元技术进行了考虑应变依赖性的硬涂层板振动特性分析，其主要利用的是ANSYS软件。也有一些学者通过自行研发复合壳单元来求解黏弹性阻尼圆柱壳的动力学特性。例如， Chakravorty等[15]研发了8节点曲面四边形等参单元来模拟黏弹性圆柱壳。Masti等创建了一个包括基体层、黏弹性阻尼层和约束层的8节点80自由度的复合曲面单元，并用该单元对复合圆柱壳的振动特性进行了分析。面向特定的圆柱壳复合结构，通过自行研发有限元程序来对其进行建模与分析有很好的灵活性及较高的计算效率。因而，本文也按此思路开展硬涂层圆柱壳的动力学建模及分析工作。

在考虑硬涂层材料应变依赖性的前提下，开发了一种复合圆柱壳单元，并在此基础上，提出了一种简化的硬涂层圆柱壳复合结构非线性振动特性的迭代求解方法(Simplified Hard-Coating Cylindrical Shell Iteration Method, SHCIM)。同时，以NiCoCrAlY+YSZ硬涂层圆柱壳为例，对其线性和非线性振动特性进行求解，并将线性结果与ANSYS进行对比，以验证该复合圆柱壳单元的正确性和适用性。

1 复合圆柱壳单元

如图1所示，基础激励作用下的硬涂层圆柱壳结构，分别由厚度为Ts的金属基体和厚度为Tc的外敷硬涂层构成。

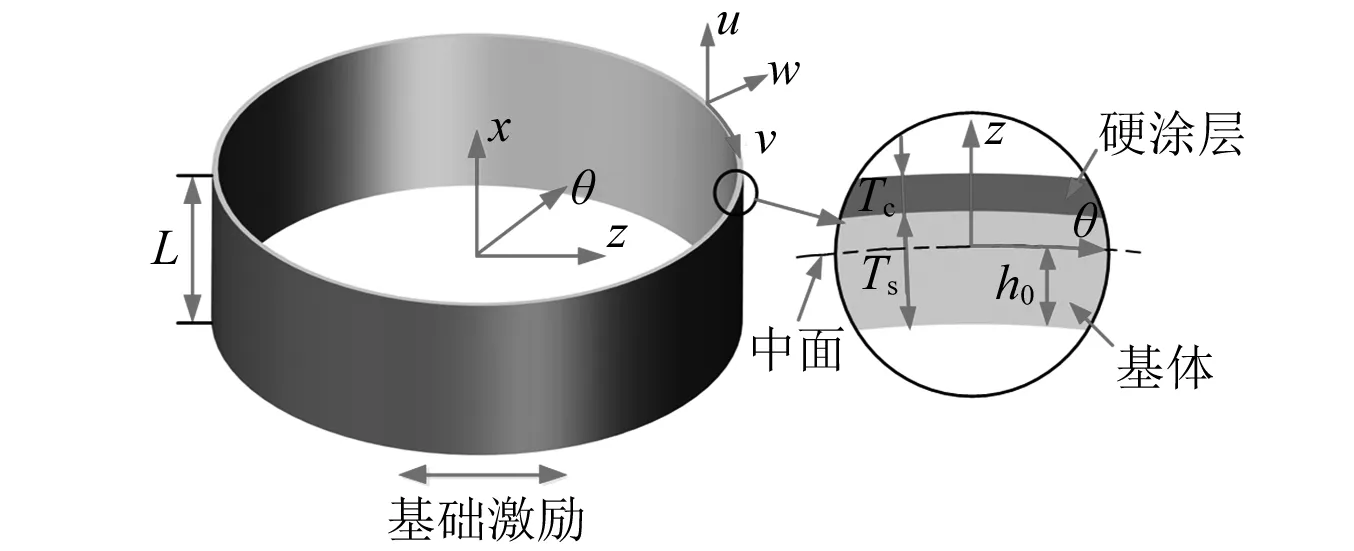
图1 硬涂层圆柱壳复合结构示意图Fig.1 The composite structure of hard-coating cylindrical shell

沿复合结构中面的主曲率线和法线方向建立正交曲线坐标系(x，θ，z)，相对应的中面位移分别为u，v和w。中面到圆柱壳内表面的距离h0可表示为

(1)

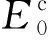
(2)

其中，

(3)

进一步可将式(2)表达为

(4)

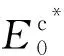
(5)

为与应变依赖性相关的材料参数。

为更好地求解此硬涂层圆柱壳复合结构的非线性振动特性，本文开发了一种4节点36自由度的复合圆柱壳单元，如图2所示。该单元每个节点包含9个自由度，分别定义为

(6)

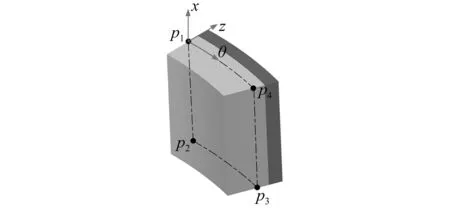
图2 复合圆柱壳单元Fig.2 The composite cylindrical shell element

基于小应变假设，且假设变形后复合圆柱壳中面法线与中面垂直，单元中面上任一点的位移w(u,v具有相同的表达形式)可定义为

w=a1+a2x+a3θ+a4x2+a5xθ+a6θ2+a7x3+
a8x2θ+a9xθ2+a10θ3+a11x3θ+a12xθ3

(7)

则单元中面上任一点的位移场可表示为

{u，v,w}T=Nd

(8)

式中：d为36×1阶的单元位移向量；N为3×36阶的单元形函数矩阵；可表示为

N=[Np1,Np2,Np3,Np4]

(9)

其中，

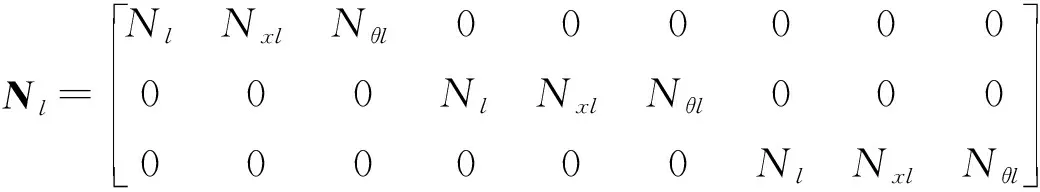
(10)

单元内的应变-位移关系可表示为

ε=Bd

(11)

式中：B即为应变矩阵，可表示为

B=[Bp1,Bp2,Bp3,Bp4]

(12)

(13)

(14)

(15)

(16)

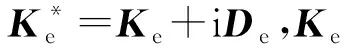
f={0,μθρa,μzρa}T

(17)

式中：a为基础的绝对加速度；μθ和μz均为影响系数，在与基础激励方向一致的自由度上，影响系数取为1，否则取为0。

2 考虑应变依赖性的硬涂层圆柱壳的振动特性计算

整个硬涂层圆柱壳复合结构的动力学方程可表示为

(18)

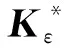
(19)

式中：Kε为刚度矩阵；D为与硬涂层损耗因子相关的材料阻尼矩阵。F为按正弦变化的外部基础激励向量；x为节点位移向量；可表示为

x=φNq

(20)

式中：φN为节点正则振型矩阵；q为节点正则坐标响应。

将式(20)代入式(18)可得到正则化的动力学方程，即为

(21)

其中，

(22)

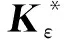
(23)

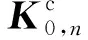
(24)

式中：Vel为单元中硬涂层的体积；hel可通过式(25)计算

(25)

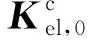
由于式(23)需对每个单元中硬涂层的等效应变进行计算，为加快计算速度，本文利用最大等效应变作如下简化

(26)

2.1 共振响应的计算

采用Newton-Raphson法求解硬涂层圆柱壳的非线性振动响应，具体流程如图3所示。

定义残差向量为

(27)

如将描述硬涂层材料的多项式的阶数取n=3，并将式(24)和式(26)代入式(27)可得

(28)

定义雅可比矩阵J为

(29)

式中：Re( )和Im( )分别为求括号内表达式的实部和虚部的函数；∂r/∂qR和∂r/∂qI分别为残差向量r对q的实部qR和虚部qI求偏导。

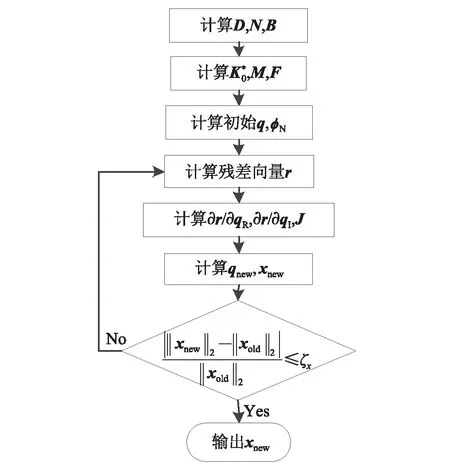
图3 硬涂层圆柱壳的非线性共振响应计算过程Fig.3 Nonlinear resonance response analysis process of hard-coating cylindrical shell

则此非线性动力学方程的迭代格式可表示为

(30)

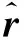
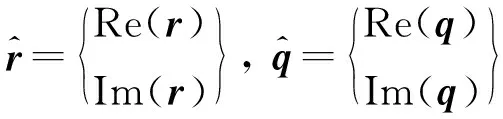
(31)

(32)

则节点位移向量xnew为

(33)

共振响应的迭代终止条件可定义为

(34)

式中：| |和‖‖2分别为取绝对值函数和取2范数函数；ζx为振动响应求解精度。

2.2 共振频率的计算

共振频率的具体迭代过程，如图4所示。

图4 硬涂层圆柱壳的非线性共振频率计算过程Fig.4 Nonlinear resonance frequency analysis process of hard-coating cylindrical shell

由式(32)求出qnew后，便可通过式(22)求得硬涂层的等效应变εe，进而根据式(24)更新硬涂层圆柱壳的总复刚度矩阵，硬涂层圆柱壳复合结构的共振频率可通过式(35)进行求解

(35)

式中：ω=2πf(p)，p为共振频率阶次。

第p阶共振频率的迭代终止条件可定义为

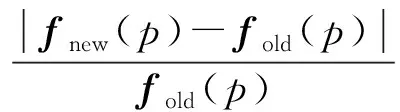
(36)

式中：ζf为共振频率的求解精度。

3 研究实例

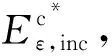
(37)

(38)

该硬涂层圆柱壳的相关材料和几何参数，如表1和表2所示。其中，表1中的储能模量和损耗因子为应变为0时的取值。

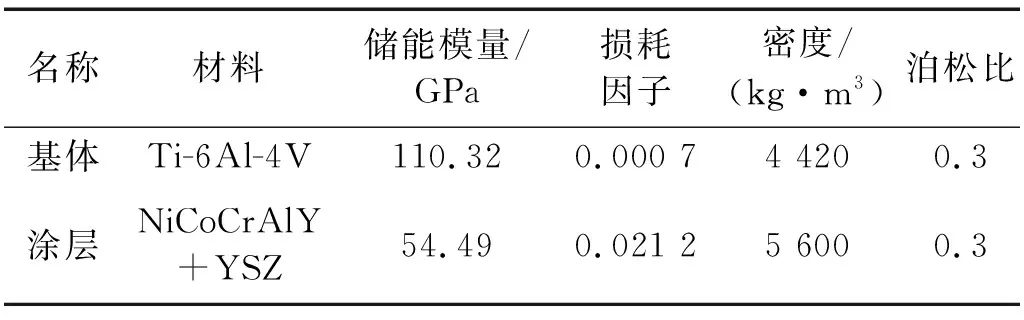
表1 硬涂层圆柱壳材料参数

表2 硬涂层圆柱壳几何参数

3.1 硬涂层圆柱壳的线性振动特性分析

利用复合圆柱壳单元建立有限元模型，如图5所示。该有限元模型的网格大小为15 mm，其所包含的节点总数为480，单元总数为420。同时，为在ANSYS中获得相对较为精确的计算结果，须将有限元模型的网格进行一定的细化(网格大小设为1 mm)，细化后的有限元模型的节点总数为85 824个，单元总数为84 930个，如图6所示。

根据本文所提出的简化的硬涂层圆柱壳非线性振动特性的迭代求解方法(应变为0时)，得到了前5阶的线性共振频率，并与ANSYS线性结果进行对比，如表3所示。

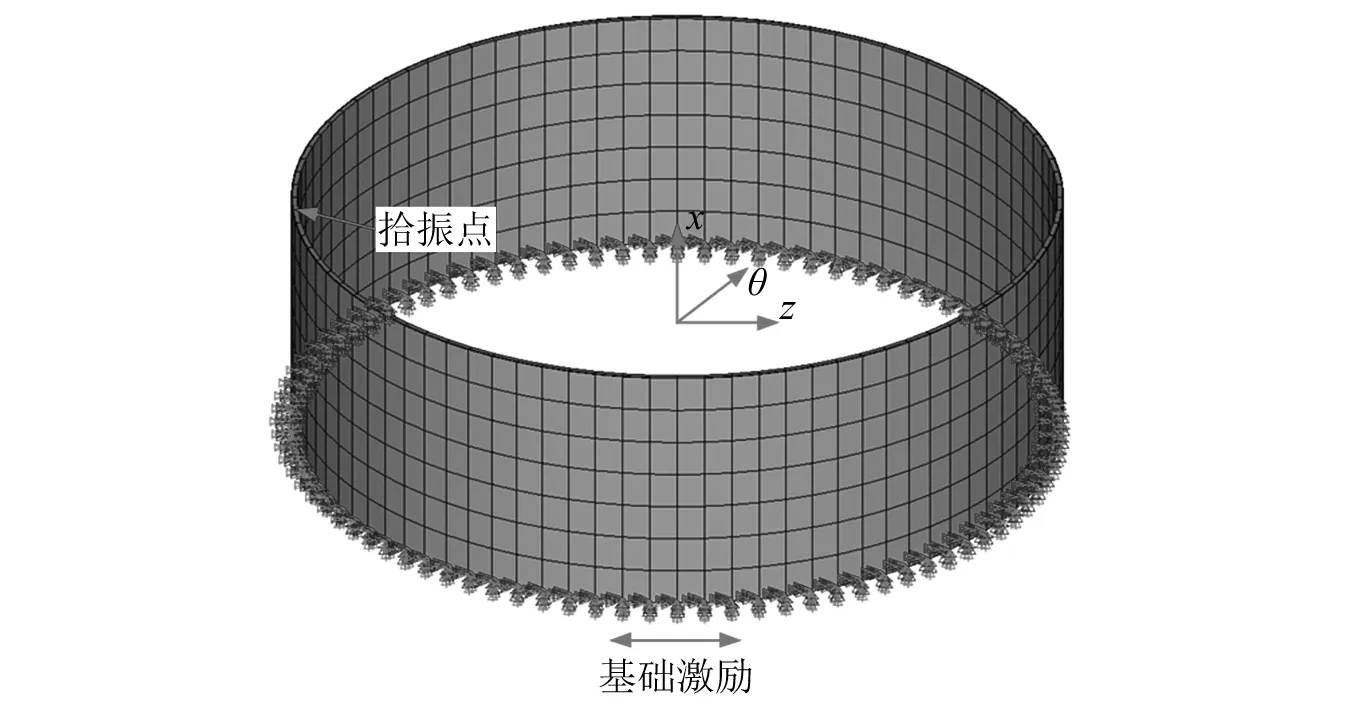
图5 SHCIM硬涂层圆柱壳有限元模型Fig.5 The finite element model of hard-coating cylindrical shell of SHCIM

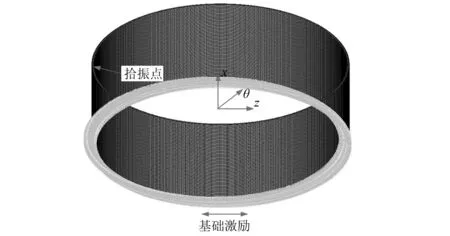
图6 细化的ANSYS硬涂层圆柱壳有限元模型Fig.6 The refined finite element model of hard-coating cylindrical shell of ANSYS

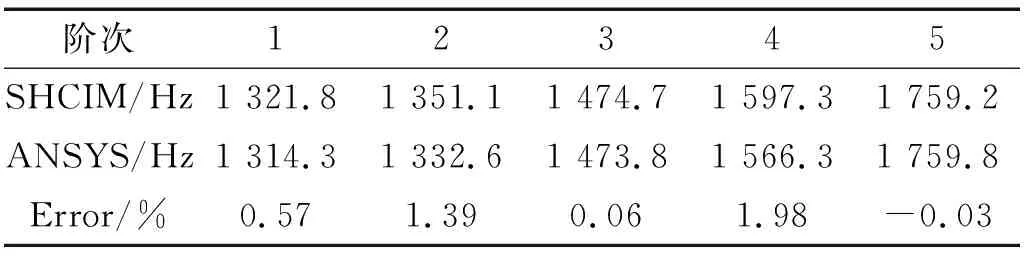
阶次12345SHCIM/Hz 1 321.81 351.11 474.71 597.31 759.2ANSYS/Hz1 314.31 332.61 473.81 566.31 759.8Error/%0.571.390.061.98-0.03

从表3可知，本文各阶的线性共振频率与ANSYS计算结果基本一致，各阶共振频率的平均误差约为0.81%，而最大误差约为1.98%。

任意提取某一阶的结果，本文以第2阶为例，SHCIM与ANSYS的硬涂层圆柱壳第2阶振型图对比，如图7所示。其振型与ANSYS基本一致。在基础激励幅度分别为1g,3g,5g,7g,9g条件下，对硬涂层圆柱壳的线性共振响应进行计算，并与ANSYS线性结果进行对比，如表4所示。

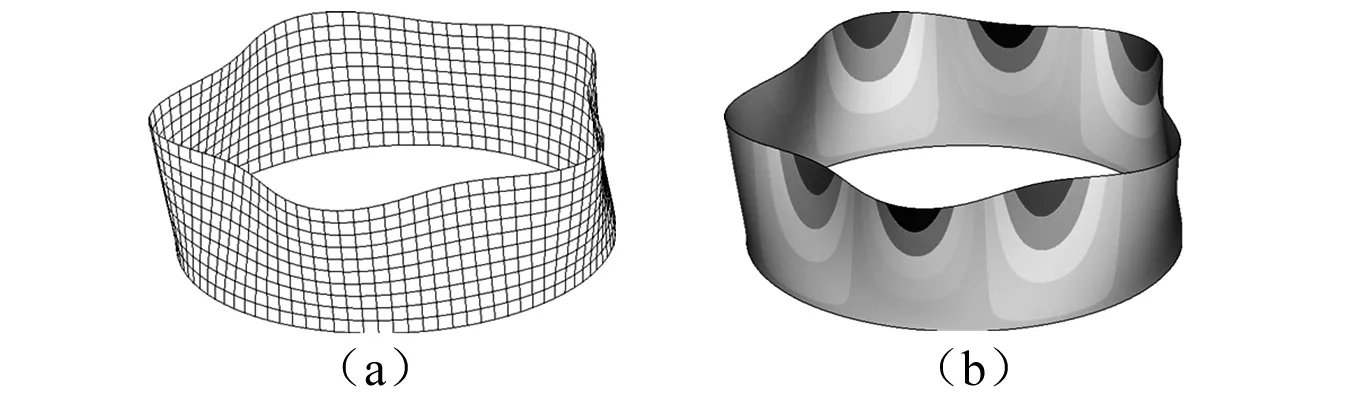
图7 SHCIM与ANSYS的硬涂层圆柱壳第2阶振型对比Fig. 7 The 2nd-order modal shapes of hard-coating cylindrical shell calculated by SHCIM and ANSYS

激励幅度1g3g5g7g9gSHCIM/(m·s-1)0.258 10.774 51.290 91.807 32.323 7ANSYS/(m·s-1)0.259 70.785 91.292 31.763 02.322 6Error/%-0.61-1.45-0.112.510.05

从表4可知，本文不同激励幅度下的线性共振响应的计算结果与ANSYS基本一致，各激励幅度下的共振响应平均误差约为0.95%，而最大误差约为2.51%。

由此可以看出，本文所开发的复合圆柱壳单元的计算结果与ANSYS基本一致，最大误差约为2.51%，而其有限元模型的网格密度仅约为ANSYS的1/15，验证了该复合圆柱壳单元的正确性和适用性。

3.2 硬涂层圆柱壳的非线性振动特性分析

基于图5中的复合圆柱壳单元和本文所提出的简化的硬涂层圆柱壳非线性振动特性的迭代求解方法，得到了硬涂层圆柱壳前5阶的非线性共振频率，及其在基础激励幅度分别为1g,3g,5g,7g,9g下的非线性共振响应(以第2阶为例)，如表5和表6所示。

表5 各激励幅度下硬涂层圆柱壳第2阶非线性共振频率

表6 各激励幅度下硬涂层圆柱壳第2阶非线性共振响应

为更好地分析NiCoCrAlY+YSZ硬涂层的应变依赖性对硬涂层圆柱壳复合结构的共振频率和共振响应的作用效果，将硬涂层圆柱壳在第2阶共振频率附近的线性和非线性频域响应绘制,如图8所示。

从图8可知，随着激励幅度的增加，硬涂层圆柱壳的非线性共振频率相对于线性的逐渐变小，说明硬涂层使复合壳具有软式非线性特点。另外，从共振响应上看，在同一激励幅度下，非线性计算获得的共振响应值小于线性计算结果，这或许说明硬涂层的应变依赖性特点对减振是有利的。

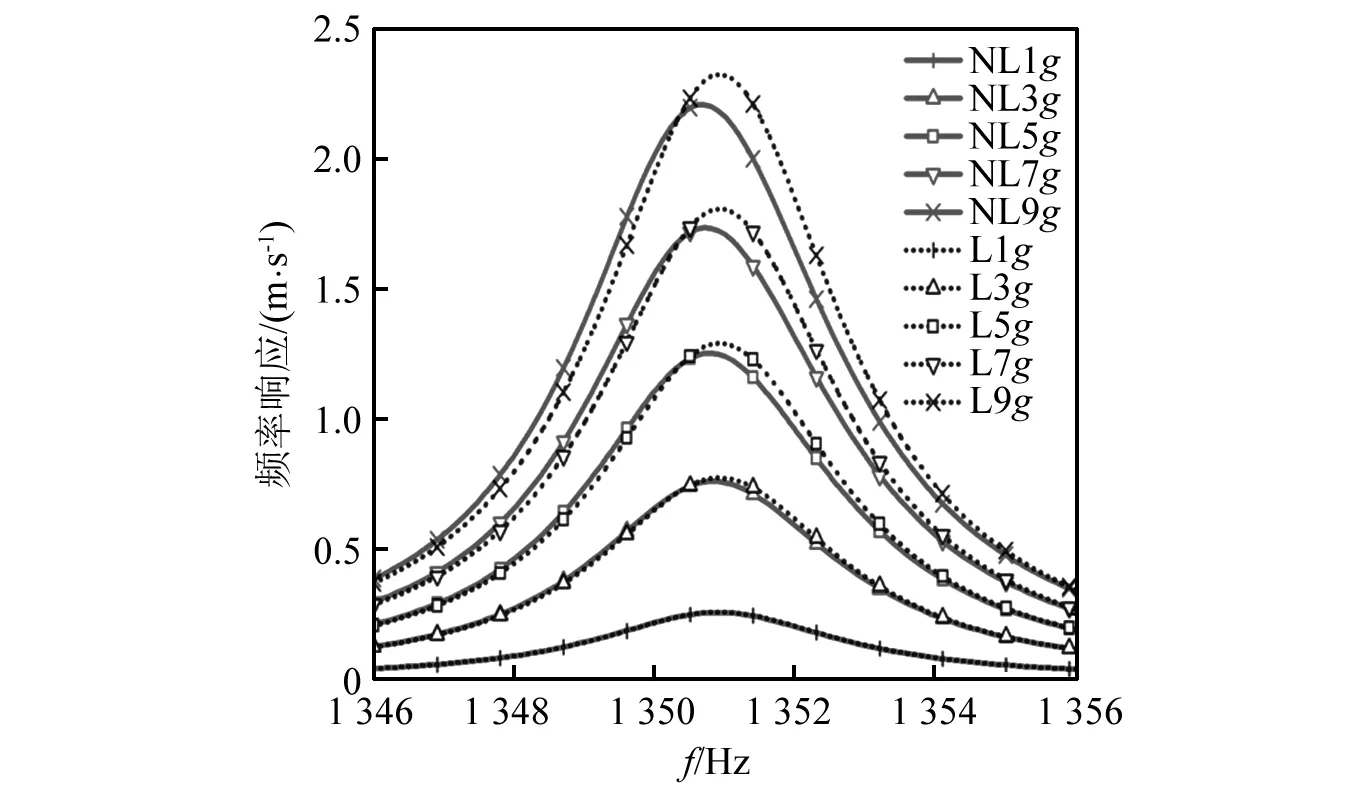
图8 硬涂层圆柱壳第2阶共振频率附近的线性和非线性频域响应Fig.8 Frequency domain responses of hard-coating cylindrical shell near the 2nd-order resonance frequency

4 结 论

(1)在考虑硬涂层应变依赖性的前提下，开发了一种4节点36自由度的复合圆柱壳单元，其线性计算结果与ANSYS基本一致，最大误差约为2.51%，而有限元模型的网格密度却仅为ANSYS的1/15，验证了该复合圆柱壳单元的正确性和适用性。

(2)基于复合圆柱壳单元和Newton-Raphson法，提出了一种简化的硬涂层圆柱壳非线性振动特性的迭代求解方法。

(3)随着激励幅度的增加，硬涂层圆柱壳的非线性共振频率相对于线性的逐渐变小，说明硬涂层使复合壳具有软式非线性特点。另外，从共振响应上看，同一激励幅度下非线性的共振响应值均小于其线性计算结果，这或许说明硬涂层的应变依赖性特点对减振是有利的。

参 考 文 献

[ 1 ] CHEN L H, HUANG S C. Vibration attenuation of a cylindrical shell with constrained layer damping strips treatment[J]. Computers & Structures, 2001, 79(14): 1355-1362.

[ 2 ] MASTI R S, SAINSBURY M G. Vibration damping of cylindrical shells partially coated with a constrained viscoelastic treatment having a standoff layer[J]. Thin-Walled Structures, 2005, 43(9): 1355-1379.

[ 3 ] 石慧荣, 高溥, 李宗刚, 等. 局部约束阻尼柱壳振动分析及优化设计[J]. 振动与冲击, 2013, 32(22): 146-151.

SHI Huirong, GAO Pu, LI Zonggang, et al. Vibration analysis and optimization design of a cylindrical shell treated with constrained layer damping [J]. Journal of Vibration and Shock, 2013, 32(22): 146-151.

[ 4 ] IVANCIC F, PALAZOTTO A. Experimental considerations for determining the damping coefficients of hard coatings[J]. Journal of Aerospace Engineering, 2005, 18(1): 8-17.

[ 5 ] BLACKWELL C, PALAZOTTO A, GEORGE T J, et al. The evaluation of the damping characteristics of a hard coating on titanium[J]. Shock and Vibration, 2007, 14(1): 37-51.

[ 6 ] FILIPPI S, TORVIK P J. A methodology for predicting the response of blades with nonlinear coatings[J]. Journal of Engineering for Gas Turbines and Power, 2011, 133(4): 042503.

[ 7 ] REED S A, PALAZOTTO A N, BAKER W P. An experimental technique for the evaluation of strain dependent material properties of hard coatings[J]. Shock and Vibration, 2008, 15(6): 697-712.

[ 8 ] TORVIK P J. Determination of mechanical properties of non-linear coatings from measurements with coated beams[J]. International Journal of Solids and Structures, 2009, 46(5): 1066-1077.

[ 9 ] SUN W, LIU Y. Vibration analysis of hard-coated composite beam considering the strain dependent characteristic of coating material[J]. Acta Mechanica Sinica (AMS), 2016, 32(4): 731-742.

[10] SUN W, LIU Y, DU G. Analytical modeling of hard-coating cantilever composite plate considering the material nonlinearity of hard coating[J]. Mathematical Problems in Engineering, 2015, 2015: 1-14.

[11] ZHENG L, QIU Q, WAN H, et al. Damping analysis of multilayer passive constrained layer damping on cylindrical shell using transfer function method[J]. Journal of Vibration and Acoustics, 2014, 136(3): 031001.

[12] 李晓妮, 向宇, 黄玉盈, 等. 基于传递矩阵法分析 ACLD 圆柱壳振动控制问题的一种完全力电耦合模型[J]. 振动与冲击, 2011, 30(6): 147-152.

LI Xiaoni, XIANG Yu, HUANG Yuying, et al. Fully coupled electro-mechanical model based on transfer matrix method for vibration control of circular cylindrical shell with active constrained layer damping [J]. Journal of Vibration and Shock, 2011, 30(6): 147-152.

[13] JIN G, YANG C, LIU Z, et al. A unified method for the vibration and damping analysis of constrained layer damping cylindrical shells with arbitrary boundary conditions[J]. Composite Structures, 2015, 130: 124-142.

[14] LI H, YING L, SUN W. Analysis of nonlinear vibration of hard coating thin plate by finite element iteration method[J]. Shock and Vibration, 2014, 21: 1-12.

[15] CHAKRAVORTY D, BANDYOPADHYAY J N, SINHA P K. Finite element free vibration analysis of point supported laminated composite cylindrical shells[J]. Journal of Sound and Vibration, 1995, 181(1): 43-52.

[16] SUN W, ZHU M W, WANG Z. Free vibration analysis of a hard-coating cantilever cylindrical shell with elastic constraints[J]. Aerospace Science and Technology, 2017,63: 232-

244.

[17] SUN W, WANG Z, ZHU M W, et al. Identifying the mechanical parameters of hard coating with strain dependent characteristic by an inverse method[J]. Shock and Vibration, 2015(2): 1-15.