沥青混合料疲劳损伤模型参数实验研究
张立文,代茂华,苑红凯,孙大权
(1.天津市市政工程设计研究院,天津市 300051;2.同济大学,上海市 201804)
1 沥青混凝土疲劳损伤损伤模型选择
自愈合主要存在于沥青损伤断裂过程区,所以沥青混合料疲劳损伤过程中的裂纹尖端断裂过程区的尺寸及数量同其愈合行为密切相关。沥青混合料疲劳损伤的程度和自身损伤状态需要采用疲劳损伤理论进行解释和标定。文章在总结国内外沥青混凝土疲劳损伤模型的基础上,选择了合理疲劳损伤自愈合模型,通过进行疲劳损伤实验设计,获得沥青类材料疲劳损伤特性参数,为计算材料疲劳损伤程度奠定了基础。
1.1 疲劳累积损伤模型
研究人员基于损伤理论提出了一些损伤累积模型,构成了不同的疲劳累积损伤理论,见表1。

表1 疲劳累积损伤理论分类[1]
杨晓华[1]将现有疲劳累积损伤理论分成两大类:线性的等损伤累积理论和非线性的等损伤累积理论,习惯上称为线性累积损伤理论和非线性累积损伤理论。其中比较典型的为Lemaitre模型,Lemaitre[2]从热力学势出发给出了在考虑应力幅影响的情况下,损伤演化方程为:疲劳寿命NF=的材料参数,B还依赖于平均
1.2 国内外的沥青类材料疲劳损伤的模型探索
在疲劳损伤模型的建立与疲劳损伤理论应用于沥青路面结构分析方面,国外已经做了不少的工作,见表2。
1.3 文章损伤模型主要考虑
对疲劳损伤模型的研究的目的是将损伤程度作为表征结构服务状态指标,对于疲劳损伤累积模型或者是疲劳损伤程度的演化过程和演化机理并非文章的重点,所以选择合理恰当的损伤模型成文章的主要考虑因素,虽然基于宏观的研究方法不探究损伤的物理背景和材料内部的细观结构变化,也不能从细、微观结构层次上弄清损伤的形态与变化。但是所有的细观与微观的数量的累积表现为宏观的力学特征,具有明确的物理意义,可直接反映结构的受力状态,用宏观方法建立的损伤本构方程便于应用到结构设计、寿命计算及安全分析中。所以文章采用唯象的宏观本构理论,针对非线性疲劳累积损伤理论更能准确描述沥青混合料的疲劳累积损伤程度,并且根据前述Lemaitre疲劳累积损伤模型在沥青及沥青混合料较为广泛,所以选用该模型作为文章损伤累积模型。
2 沥青混合料疲劳损伤模型参数实验研究
Lemaitre模型中损伤度的表达式为D=1-似于有效应力大小成正比,即γ=0,得到:

表2 国内外的沥青类材料疲劳损伤的模型

将公式取对数得到
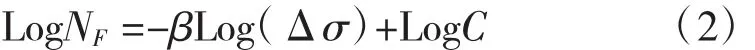
其中,LogC=-Log(β+1)+βLog(2B)
方程中沥青混合料疲劳损伤特性参数NF和β可以根据不同应力条件下的疲劳实验数据,采用最小二乘法拟合得到[11]。
2.1 沥青混合料疲劳损伤实验设计
(1)疲劳试验及加载模式的选择
进行室内小型试件的疲劳试验通常有直接拉伸试验、弯曲试验和劈裂试验三种方法,直接拉伸试验需要粘结固定试件端部,试样制备方法稍慢;而考虑到后期的材料愈合行为研究需要固定的养护时间,劈裂试验方法不利于后期养护实施,而直接拉伸试验的受力模式和愈合养护更为简便,故选用小梁弯曲疲劳实验作为文章的疲劳实验方式。
室内小型试件的疲劳试验通常采用控制应力和控制应变两种不同的加载模式。由于控制应力加载方式简便宜行,文章中所有疲劳实验均采用控制应力方式进行。
(2)沥青混合料组成设计
采用70#沥青,按照规范要求,某拟定AC-13连续级配,最佳油石比为4.6%。
2.2 沥青混合料疲劳损伤参数拟合
采用万能材料试验机(MTS)进行三点弯曲疲劳试验,选用上节中70#沥青制作AC-13密级配矿料沥青混合料,试件采用轮碾成型后切割成规定尺寸的制作方法。采用10 Hz的半正矢波作为加载波形,进行15℃疲劳试验,相邻波形间没有间歇时间。疲劳实验结果在双对数条件下,沥青混合料的疲劳曲线见图1。

图1 沥青混合料疲劳方程
从图1可知,通过不同应力下沥青混合料的疲劳实验得到疲劳方程:
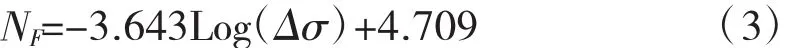
不同应力比条件下,沥青混合料的疲劳寿命为见表3。
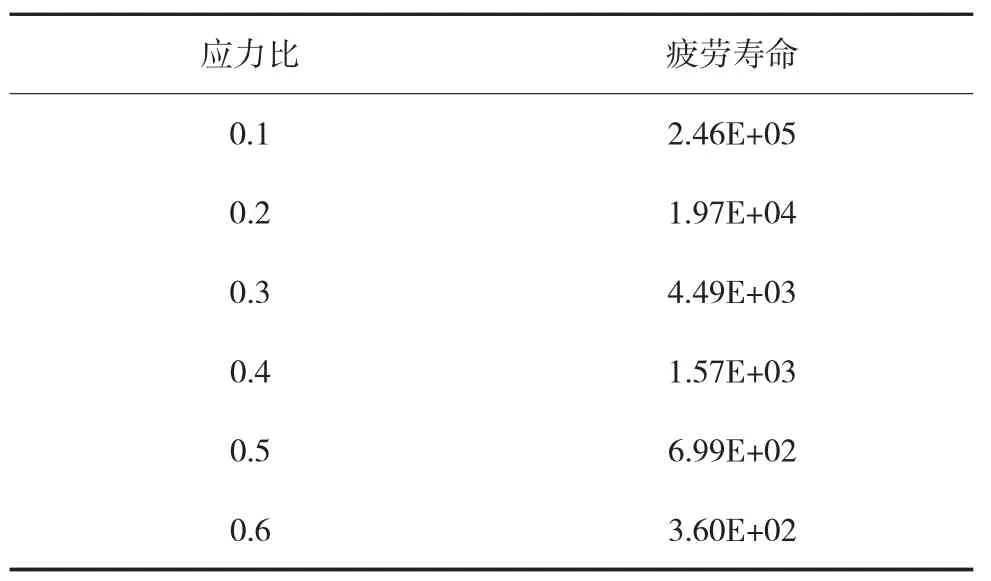
表3 不同应力下混合料疲劳寿命
由前述可知,β=3.643,沥青混合料的疲劳损伤方程为:
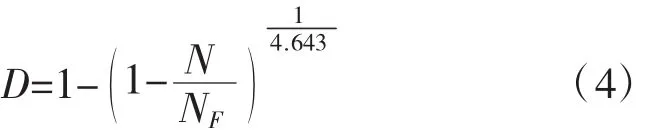
获得沥青混合料疲劳损伤方程后,可以根据该应力水平下的疲劳寿命NF和疲劳特性参数β,确定沥青混合料的疲劳损伤程度。
3 沥青胶浆疲劳损伤模型参数实验研究
3.1 沥青胶浆疲劳损伤实验设计
(1)疲劳加载方式及实验设备
沥青胶浆的疲劳加载方式与混合料相同,但沥青胶浆实验难以采用梁式试件加载,所以采用动态剪切流变仪(DSR)作为沥青疲劳加载实验设备。采用控制应力条件下的试件扫描。
(2)沥青及矿粉
以基质沥青作为对比样本,采用1∶0、5∶1、2.5∶1、1∶1四种胶粉比作为疲劳损伤研究对象。
(3)沥青胶浆制备工艺
将沥青和矿粉采用搅拌方法制备成沥青胶浆。具体制备方法如下:
a.确定制备的沥青胶浆的总量(500 g左右);
b.根据沥青和矿粉按掺配比例,分别准备所需的70#基质沥青和矿粉;
c.把准备的基质沥青加入到搅拌用的金属拌锅中,待温度升高至160℃左右时,将矿粉徐徐加入盛有沥青的金属拌锅里,边加热边用搅拌棒搅拌,保持沥青温度在160℃~170℃的范围内,开动搅拌机搅拌30 min后,沥青胶浆制备完毕,保温以备试样浇筑使用。
3.2 沥青胶浆疲劳损伤参数拟合
3.2.1 沥青胶浆疲劳实验基本参数设定
考虑到沥青的非线性疲劳损伤以及低温粘结问题,本文中所有的沥青及沥青胶浆疲劳试验均采用25℃,10 Hz条件下进行。主要步骤如下:
(1)测定沥青PG分级;
(2)按照老化沥青混合料PG分级实验成型DSR试件,并压缩至2 mm标准试样高度;
(3)水槽注水保温,设定目标温度为沥青材料PG分级的高温温度t;
(4)在温度t下保温10 min后,设定目标温度为实验温度25℃;
(5)25℃下保温15 min以上,即可以开始进行沥青的疲劳实验。
3.2.2 沥青胶浆疲劳实验结果
根据文献[12],由于采用应力水平较小,故不考虑沥青的非线性粘弹性效应,不同应力水平下各种沥青胶浆的疲劳寿命见图2。
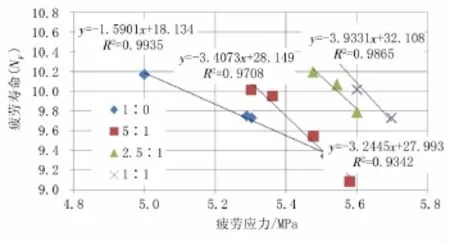
图2 沥青胶浆不同应力下疲劳寿命
图 2 中 1∶0,5∶1,2.5∶1,1∶1 分别代表沥青:矿粉之比。
从图2可知,通过不同应力下沥青胶浆的疲劳实验得不同沥青胶浆的疲劳方程见表5,不同应力比条件下,沥青混合料的疲劳寿命为见表6,不同沥青胶浆的疲劳损伤方程见表7。

表5 疲劳方程汇总

表6 不同沥青胶浆的疲劳损伤方程
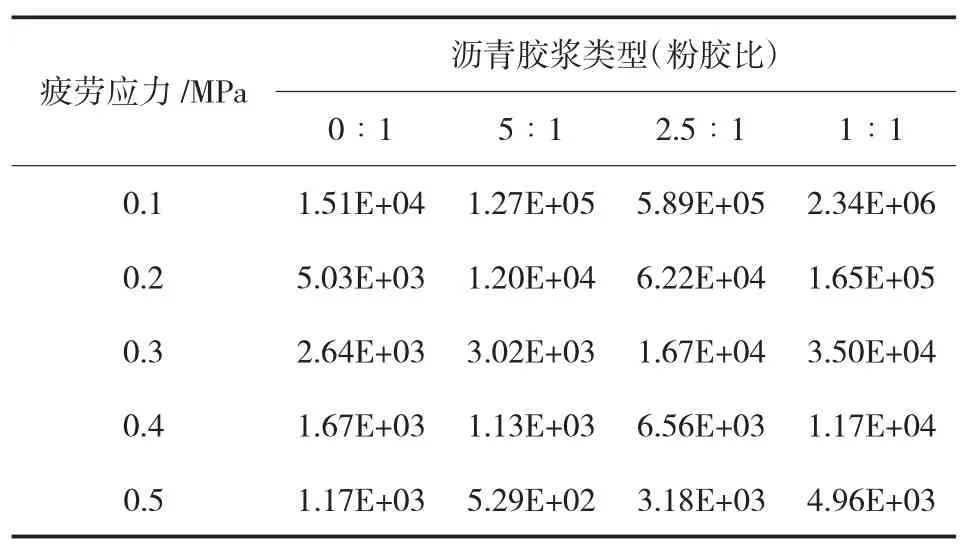
表7 不同应力下沥青胶浆疲劳寿命
获得不同沥青胶浆的疲劳损伤方程后,可以根据该应力水平下的疲劳寿命NF和疲劳特性参数β,按照模型所述,确定沥青胶浆的疲劳损伤程度。
4 结语
沥青类材料的自愈合行为同所处的服务期限状态密切相关,疲劳损伤程度可以通过疲劳损伤方程来准确描述。本文通过文献资料调研,和室内研究得出如下结论:
(1)用宏观的损伤力学方法可以准确描述材料宏观整体的力学服务状态的变换,并且可以采用Lemaitre疲劳累积损伤模型来准确描述沥青混合料的疲劳累积损伤规律。
(2)通过15℃、10 Hz、不同应力比条件下的室内小梁疲劳实验标定了特定类型的沥青混合料的疲劳损伤模型,y=-1.590x+18.13。
(3)通过25℃,10 Hz,不同应力比条件下的DSR的重复剪切疲劳损伤试验标定了特定类型的沥青胶浆的疲劳损伤模型。
(4)通过模型的标定确定了对不同应力比条件下沥青及沥青混合料的疲劳寿命预测值。
文章通过进行疲劳损伤实验设计,获得沥青类材料疲劳损伤特性参数,为计算材料疲劳损伤程度奠定了基础。
[1]杨晓华,姚卫星,段成美.确定性疲劳累积损伤理论进展[J].中国工程科学,2003,5(4):81-87.
[2]Lemaitre J.,Chaboche J.L..Aspects phenomenologique de la rupture par endommagement[J].J.de.Meca.Appl.,1978(2):317-365.
[3]关宏信.沥青混合料粘弹性疲劳损伤模型研究[D].湖南长沙:中南大学,2005.
[4]周志刚.交通荷载下沥青类路面疲劳损伤断裂研究[D].湖南长沙:中南大学,2003.
[5]唐雪松,蒋持平,郑健龙.沥青混合料疲劳过程的损伤力学分析[J].应用力学学报,2000(4):92-98.
[6]孙志林.全厚式沥青路面结构粘弹性疲劳损伤过程研究[D].江苏南京:东南大学,2007.
[7]张久鹏.基于粘弹性损伤理论的沥青路面车辙研究[D].江苏南京:东南大学,2008.
[8]赖正聪.半刚性基层疲劳损伤模型及寿命预估.科学技术与工程,2012,12(8):
[9]R.A.Sehapery.Models for Damage Growth and Fracture in Nonlinear Viscoelastic Particulate Composites[A].Proe.9th U.S.National Congress ofApplied Mech.,American Society ofMechanical Engineers[C].1982,237-245.
[10]R.A.Schapery.Nonlinear Constitutive Equations for Solid Propellant Based 011 a work Potential and Mieromechanical Model[A].Proc.JANNAF Structures and Mechanical Behavior Meeting[C].CPIA,Huntsville,AL,1987.
[11]同济大学数学教研室.数理统计的原理与方法[M].上海:同济大学出版社,2010.
[12]J.Anderson,Christensen,,D.W,etc.Binder Characterization and Evaluation (SHPR-A-369),Vo3[M].Physical Characterization,SHRP,National Research Council,1994.

