地铁车辆预防性维修周期优化模型研究

钮海彦

(无锡地铁集团有限公司，214121，无锡//工程师)

在地铁车辆预防性维修计划的制定过程中，维修周期的确定是非常重要的[1]。维修周期过长，则无法满足车辆的安全性和任务性要求；维修周期过短，则会导致费用过高。因此，预防性维修周期优化在满足可靠性要求下，应符合维修费用最低的原则。

1 维修费用

地铁车辆的维修费用包括在维修过程中直接消耗的人工和材料等直接费用(DMC)，以及维修管理费用、备件库存费用等间接成本(IMC)[3]。

根据维修工作的类型，参照GJB-1378A—2007《装备以可靠性为中心的维修》，维修费用可分为预防性维修费用、故障维修费用及停机损失费用。维修费用计算式为：

Cz=NpCp+NrCr+NlCl

(1)

式中：

Cz——计算期内的产品维修总费用；

Cp——进行1次预防性维修工作的费用；

Cr——进行1次故障维修的费用；

Cl——产品故障导致1次停机所产生的损失费用；

Np——计算期内的预防性维修工作次数；

Nr——计算期内的故障后维修工作次数；

Nl——计算期内故障造成的停机次数。

1.1 预防性维修费用

预防性维修工作包括对零部件的检查、测试及保养等环节。预防性维修费用Cp包括维修工时费、物料消耗费及工具使用费，其计算式为：

Cp=tpcp+cm，p+cl，p

(2)

式中：

tp——进行1次预防性维修所需的人工工时；

cp——单位工时的人工费用；

cm，p——进行1次预防性维修所需的物料费用；

cl，p——进行1次预防性维修所需的工具费用。

对于特定的地铁公司来说，cp是确定的，其计算式为：

cp=(cs+cw+ct)/tw

(3)

式中：

cs——检修工作人员的平均薪水；

cw——检修工作人员的平均福利费用；

ct——检修人员的平均培训费用；

tw——检修人员的平均工作时间。

1.2 故障维修费用

故障维修费用包括工时费、物料购置费、工具使用费及零部件更换费用。Cr的计算式为：

Cr=trcp+Pece+cm，r+cl，r

(4)

式中：

tr——进行1次故障维修所需的人工工时；

Pe——故障维修需更换零部件的概率；

ce——零部件的采购单价；

cm，r——进行1次故障维修所需的物料费用；

cl，r——进行1次故障维修所需的工具使用费用。

2 维修周期优化模型

维修周期优化模型的主要评价指标为可靠性指标和维修费用。可靠性指标主要与故障率相关。故障率越低，可靠性越好。维修费用与维修周期相关。

2.1 故障率预测模型

预防性维修周期模型必须明确在未来一段时间内的故障率变化规律。本文提出了一种基于GM(1，1)灰色模型来预测故障率的方法。

GM(1，1)模型被广泛应用于单调系统预测问题的建模。令a为发展灰数，μ为内生成控制灰数，则第(k+1)个统计区间的故障率估计值为：

(5)

Y=[x(0)(2)，x(0)(3)，…，x(0)(12)]T

式中:

x(0)——原始的故障率真实值;

x(1)——叠加得到的故障率

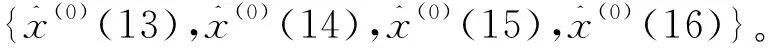
(6)

2.2 维修周期优化模型

2.2.1 维修周期模型综述

由于预防性维修周期的原则是要在满足可靠性要求的基础上使维修费用最少。在0～tz时间段内,有:

Cz，min=(NpCp+NrCr+NlCl)/tz

(7)

式中:

R(t)——t时刻的可靠度。

故在满足可靠性要求的基础上使维修费用最少的优化周期模型为：

2.2.2 潜在故障检测周期的优化模型

设备如处于可鉴别的非正常状态，若不采取预防性维修和调整措施就会发生功能障碍，则可判断该设备发生了潜在故障。一般通过状态监测或定期检查等预防性维修工作可发现潜在故障。

有的潜在故障会造成较为严重的后果，需要进行定期检测并进行视情维修。

如图1所示。在1个预防性维修周期T内，设备潜在故障在tF时刻发生，未采取措施时，功能故障在tp时刻发生，则劣化时间tPF=tp-tF。假设,在t时刻发生某潜在故障的概率为f(t)，该故障在检查期间劣化为功能故障的概率为P(t)则对于任意的机械设备，tPF为一随机变量。

由于tPF常用Weibull分布来描述。则潜在故障检测周期模型可简化为：

式中：

m，η——Weibull分布参数。

2.2.3 隐蔽功能故障检查周期优化

隐蔽功能故障是指使用者不能在设备正常使用过程中直接发现，而必须在停机后进行专门的功能检查才能发现的故障。隐蔽功能故障检查周期优化模型为：

2.2.4 定期维修周期优化模型

定期维修是指设备使用时间达到预先规定期限时，无论技术状态如何都要进行的预防性维修。定期维修周期优化模型为：

3 案例计算

以车门下挡销组件紧固螺栓松动故障为例，以维修周期优化模型进行分析计算。正常情况下，挡销与门槛嵌块导槽内壁并不接触。如果下挡销组件的紧固螺栓出现松动却未能被及时发现并修复，则可能会引起关门过程中下挡销晃动，进而导致车门无法关闭。可见本故障的维修周期优化模型是潜在故障检测周期优化模型。

3.1 维修费用计算

根据某地铁下挡销组件紧固螺栓维修成本相关数据，经计算可得，cp=36.96元/h，全线28列列车都进行1次预防性维修的费用Cp=251.72元，1次故障维修的费用为Cr=4.48元，发生功能故障后造成的损失Cl=10 000元。而下挡销组件紧固螺栓松动的故障率为λ=2.01×10-8次/km。

3.2 劣化时间分布参数

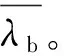
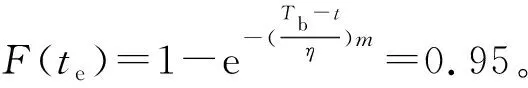
3.3 优化模型的求解

经过计算可得，当Lb=5 200 km时，cz，min=0.123 47 元/km。参考现有的修制修程可确定车门下挡销组件紧固螺栓松动的维修级别为A级，合理的检查周期应为5 000 km。

4 结语

为了确定地铁车辆预防性维修周期，建立了以“在一定可靠性基础上实现费用最低”为优化目标的地铁车辆预防性维修周期优化模型。采用潜在故障检测周期优化模型对某实际案例进行计算，得到了合理的潜在故障检测周期，可见优化模型具有计算简便、实用性强的特点，对地铁车辆的预防性维修工作有指导意义。

[1] 王伯铭. 城市轨道交通车辆总体及转向架[M].北京：科学出版社，2013.

[2] 王灵芝. 以可靠性为中心的高速列车设备维修决策支持系统研究[D].北京：北京交通大学，2011.

[3] 陈勇. 民用飞机维修成本分析与评估[D].南京：南京航空航天大学，2006.

[4] 刁海飞，蔡景，林海彬，等.基于多目标的隐蔽功能故障检测间隔优化方法研究[J].飞机设计,2014(3):33：

[5] 中国航空综合技术研究所.修理级别分析：GJB-2961—1997[S].北京:中国航空综合技术研究所,1997.

[6] 中国航空综合技术研究所.装备以可靠性为中心的维修分析：GJB-1378A—2007[S].北京:中国航空综合技术研究所,2007.