计及可转移充放电量裕度的电动汽车充放电实时调度策略
占 智,邹 波,林振智,文福拴,2,李 波,李 梁,毛建伟
(1. 浙江大学 电气工程学院,浙江 杭州 310027;2. 文莱科技大学 电机与电子工程系,文莱 斯里巴加湾 BE1410;3. 国网浙江省电力公司 电动汽车服务分公司,浙江 杭州 310007)
0 引言
随着电动汽车(EV)技术的不断发展以及国家政策的大力支持[1],EV的渗透率有望逐步提高,从而对电力系统的规划与运行产生不可忽视的影响[2-4]。
由于EV充电具有随机性,若不对大量EV的充电进行适当的管理与控制,可能会引起系统峰荷明显上升,从而对电力系统的安全与经济运行产生负面的影响[3]。近年来,EV向电力系统反向送电V2G(Vehicle to Grid)受到普遍关注,其能够为电力系统提供调频、旋转备用等辅助服务[5-7]。在不影响EV用户用电需求的前提下,需制定有序的充放电调度策略以避免对电力系统的安全与经济运行产生负面影响,同时充分发挥EV电池的储能特性,参与提供辅助服务。另外,负荷预测总是有误差的,而EV充放电具有随机性,这样在制定EV充放电调度策略时,就需要适当考虑这些不确定性因素。
在制定EV有序充放电策略方面,已有相当多的研究报道。文献[8-10]针对分时电价机制提出了EV有序充电策略,可有效地减小系统负荷峰谷差,同时降低EV用户的充电成本。文献[11]介绍了EV分层分区调度的理念,提出了基于双层优化的EV充放电调度策略。文献[12]以系统总负荷波动最小为目标建立了促进EV与系统有效互动的最优峰谷电价模型,通过制定合理的充放电电价引导用户的充放电行为。文献[13]基于对未来EV接入电力系统的时间与充放电需求等预测信息,建立了换电站与电力系统协调的多目标双层实时充放电调度模型。文献[14]考虑了EV充电的随机性,提出了EV实时优化调度方案,以实现对夜间负荷的填谷。
综上所述,虽然已有较多文献研究了EV的有序充放电调度问题,但对一些实际因素尚未给予系统的考虑,特别是影响EV参与有序充放电调度的能力,如可行的充放电调度时间、可调度电量、用户参与充放电调度的意愿等。EV参与有序充放电调度的能力不同,其参与系统调度的灵活性也就不同。
在上述背景下,本文研究了计及EV充放电负荷参与系统调度灵活性的充放电实时调度问题。首先,比较系统地考虑了EV可调度时间与可调度电量、用户参与意愿等因素,构建了量化EV充放电量调度灵活性的可转移充放电量裕度指标。在此基础上,发展了计及可转移充放电量裕度的EV充放电实时调度模型,在每个调度时段模型分两步求取充放电调度计划:第一步以调度时间区间内的系统总负荷水平的方差最小为目标优化当前时段EV总的充放电功率;第二步以未参与充放电的EV的可转移充放电量裕度最大为目标求取满足第一步所确定的EV总的充放电功率要求的充放电调度计划。第一步和第二步所构造的优化模型分别为二次规划和整数规划问题。然后,采用YALMIP/CPLEX高效求解器对所构造的优化模型进行求解。
1 EV可转移充放电量裕度
由于负荷预测存在误差,且EV充放电具有随机性,这样在每个调度时段,应优先调度充放电没有灵活性的EV进行充放电,然后调度有灵活性的EV进行充放电,以改善负荷轮廓。基于这样的考虑,本文在计及EV可调度时间与可调度电量、用户参与意愿等因素的基础上,构建了用于量化EV充放电量调度灵活性的充放电量在不同调度时段间可转移的裕度指标。
本文从配电系统调度机构的角度出发,研究通过优化管理EV的充放电策略来改善电力系统的负荷轮廓。负责EV充放电调度的机构可从电池管理系统BMS(Battery Management System)获取电池的容量和荷电状态SOC(State Of Charge)等信息;车主根据出行计划与充放电电价等信息,通过互联网平台或其他方式通知调度机构是否参与优化调度、申报预期离开充电站的时间和离开充电站时所期望的SOC等信息[9]。针对参与优化调度的EV,调度机构按照车主申报的可充电时段和要求,优化安排EV充放电调度计划以改善系统的负荷轮廓。

1.1 可转移充电电量裕度
Slow表示EV车主为了保证下一次出行顺利,预期SOC的最低值。当电池的SOC低于Slow时,EV车主会选择对EV进行充电。
定义EV在调度时段t(t=1,2,…,96)的可转移充电电量裕度Mc,t为:
(1)
其中,Tpark,t为EV自时段t开始可持续停留在充电站的时段数;Tc,t为EV自时段t开始充电至预期SOC时所需的时段数。
Mc,t无量纲,取值范围为[0,1)。当Tpark,t>Tc,t且Tc,t≠0时,可针对EV在充电站的停留时段优化其充电计划,如将EV充电负荷转移至负荷水平较低时段;当Tpark,t≤Tc,t时,停留在充电站的EV自时段t起需要连续充电,以尽可能满足充电需求;当Tc,t=0时,则EV在时段t无充电需求。
Tpark,t可表示为:
(2)
其中,tleave为EV离开充电站时所在调度时段。
为了便于调度管理,假定EV在其到达和离开充电站时所在的调度时段中均无法充电或放电。图1给出了Tpark,t的示例。

图1 Tpark,t与Tpark,h,t示例Fig.1 Example of Tpark,t and Tpark,h,t
Tc,t可表示为:
(3)
其中,Sleave为在EV离开充电站时所期望的电池SOC,即期望EV离开充电站时其SOC达到Sleave;St为EV在时段t开始时刻电池的SOC;Eb为电池容量;ηc为充电效率;Pc为充电功率;Δt为一个时段的时间间隔(本文取15min);「x⎤表示不小于x的最小整数。
1.2 可转移放电电量裕度
一般情况下,负荷水平较低时段的电价也较低,此时EV提供V2G服务的经济性不好且作用也不大,因为系统的发电调节容量较大。因此,假设EV仅在高电价时段参与放电调度。SV2G表示EV车主设定EV参与V2G的门槛值,当电池SOC高于SV2G时,EV可提供V2G服务。
定义EV在时段t的可转移放电电量裕度Mdc,t为:
(4)
其中,Tpark,h,t为EV自时段t开始持续停留在充电站的时间所覆盖的高电价时段数;Tdc,t为EV自时段t起最多可放电的时段数。
Mdc,t无量纲,取值范围为[0,1)。当Tpark,h,t>Tdc,t且Tdc,t≠0时,可针对EV停留在充电站的时间所覆盖的高电价时段内优化安排其放电计划,如将EV放电安排在负荷水平较高时段;当Tpark,h,t≤Tdc,t时,此时应优先安排EV放电,否则就无法充分利用其放电能力;当Tdc,t=0时,则EV在时段t就无放电能力。图1给出了Tpark,h,t的示例。
Tdc,t可表示为:
(5)
其中,Pdc为放电功率;⎣x」表示不大于x的最大整数。
2 计及可转移充放电量裕度的EV充放电实时调度模型
对大量EV进行充放电调度时,配电系统调度机构可以将所管辖的配电系统按照地域划分成若干区域[11],然后由各个区域对所管辖的EV进行充放电调度。本文所提充放电调度策略就是针对某一区域内的EV进行的。基于第1节所述的EV可转移充放电量裕度指标,本节构建EV充放电实时调度模型。针对每个调度时段,该模型分两步求取EV的充放电调度计划:第一步优化得到当前时段EV总的充放电功率,但并未安排具体的EV充放电调度计划;第二步求取满足第一步求得的EV总的充放电功率要求的充放电调度计划。第二步安排调度计划时以第一步求取的结果为约束,但第二步求取的结果并不影响第一步。
2.1 EV总的充放电功率实时优化
在对EV进行充放电调度时,若以全天系统总负荷水平方差最小为优化目标,则会将高负荷时段的充电需求转移至负荷水平较低时段,但EV的充放电量仅能在其停留于充电站的时段内进行转移,从而导致在高负荷时段中的负荷低谷未及时安排EV充电,进而影响削峰填谷效果。采取“分段削峰填谷”方式,即按照系统整体负荷水平划分调度时间区间,然后在每个时间区间内分别进行削峰或填谷,则可取得更好的效果。
考虑到分时电价一般是按照日负荷水平的高低来划分高/低电价时段,且EV仅在高电价时段参与V2G,因此本文参照分时电价中高/低电价时段的划分准则划分“分段削峰填谷”的调度时间区间,见图2。

图2 EV充放电的调度时间区间Fig.2 Dispatch time segments of EVs’ charging/discharging
以当前时段t所属的调度时间区间(即图2中调度时间区间1或调度时间区间2)内系统总负荷水平的方差最小化为目标优化当前时段t的EV总充放电功率,则时段t的优化目标函数可描述为:
(6)
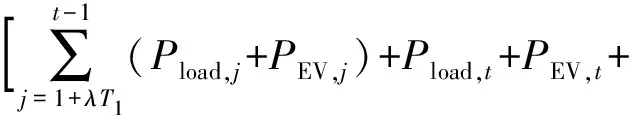
(7)
(8)
其中,t为当前时段对应的序号;Vt为时段t所属调度时间区间内系统总负荷水平的方差;λ为表征当前时段t所属调度时间区间的参数,当时段t位于调度时间区间1时有λ=0,当时段t位于调度时间区间2时有λ=1;T1和T2分别为调度时间区间1和调度时间区间2所包含的时段数;Pload,j、Pload,t和Pload,k分别为在过去时段j(j=1+λT1,2+λT1,…,t-1)、当前时段t和未来时段k(k=t+1,t+2,…,T1+λT2)除EV充放电负荷外的负荷水平;PEV,j、PEV,t和PEV,k分别为过去时段j、当前时段t和未来时段k的EV总的充放电功率,其值为正表示该时段EV整体呈充电状态,为负表示该时段EV整体呈放电状态;Pavg,t为时段t所属的调度时间区间内系统平均负荷水平。在时段t开始时刻对EV进行充放电调度,Pload,t取预测值;时段1+λT1—t-1为过去时段,Pload,j和PEV,j取实际值;时段t+1—T1+λT2为未来时段,Pload,k取预测值,Pload,t与Pload,k的预测值可采用文献[15]的方法进行预测。
在优化时段t内EV总的充放电功率时,需满足如下约束条件。
a. 当前时段t内EV总的充放电功率范围约束。
(9)
(10)
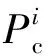
式(9)为当前时段EV总的充放电功率约束,PEV,t范围约束是在完成时段t-1的调度后,根据接入系统的EV信息确定的。
b. 未来时段k(k=t+1,t+2,…,T1+λT2)内EV总的充放电功率范围约束。
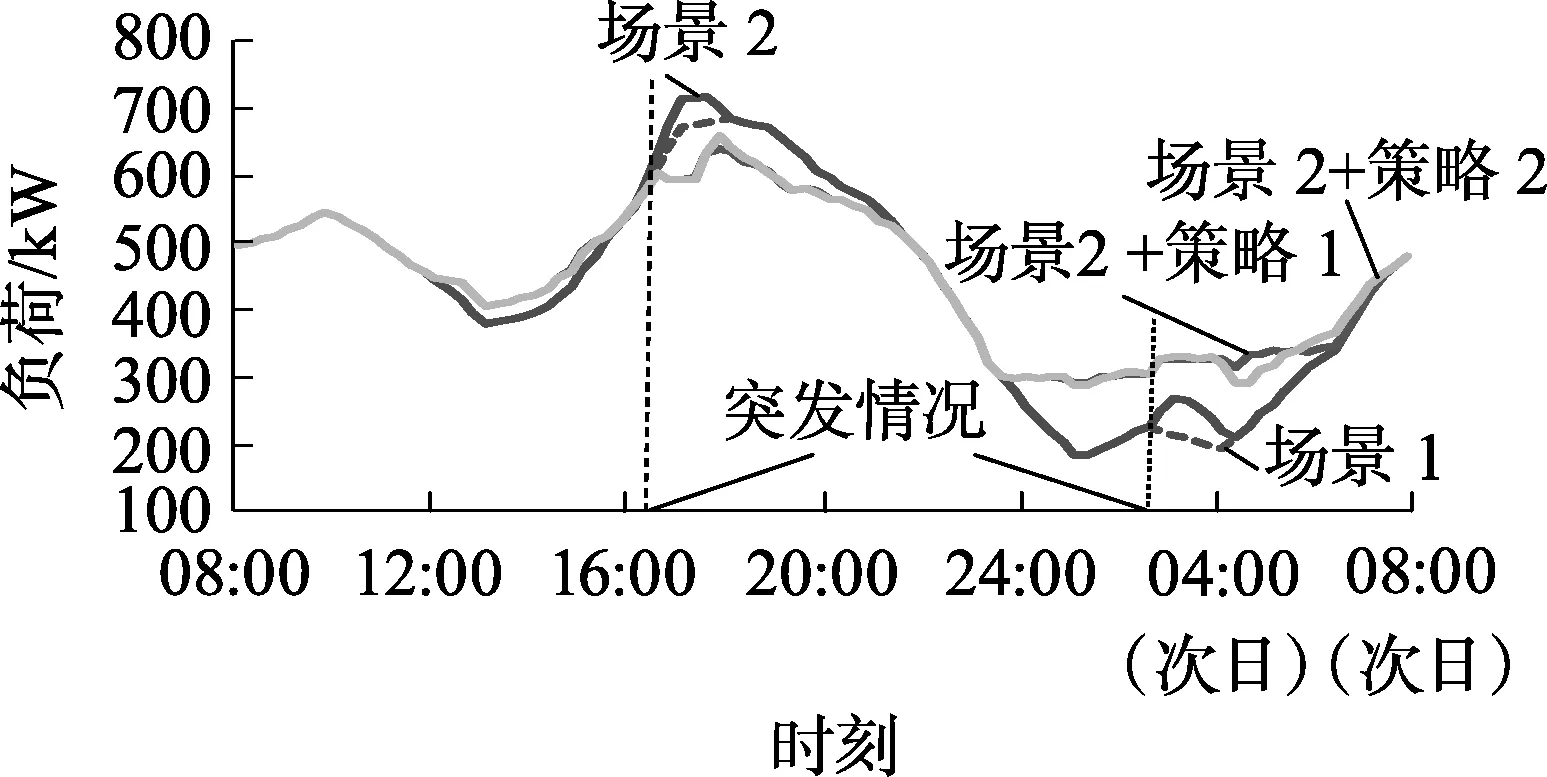
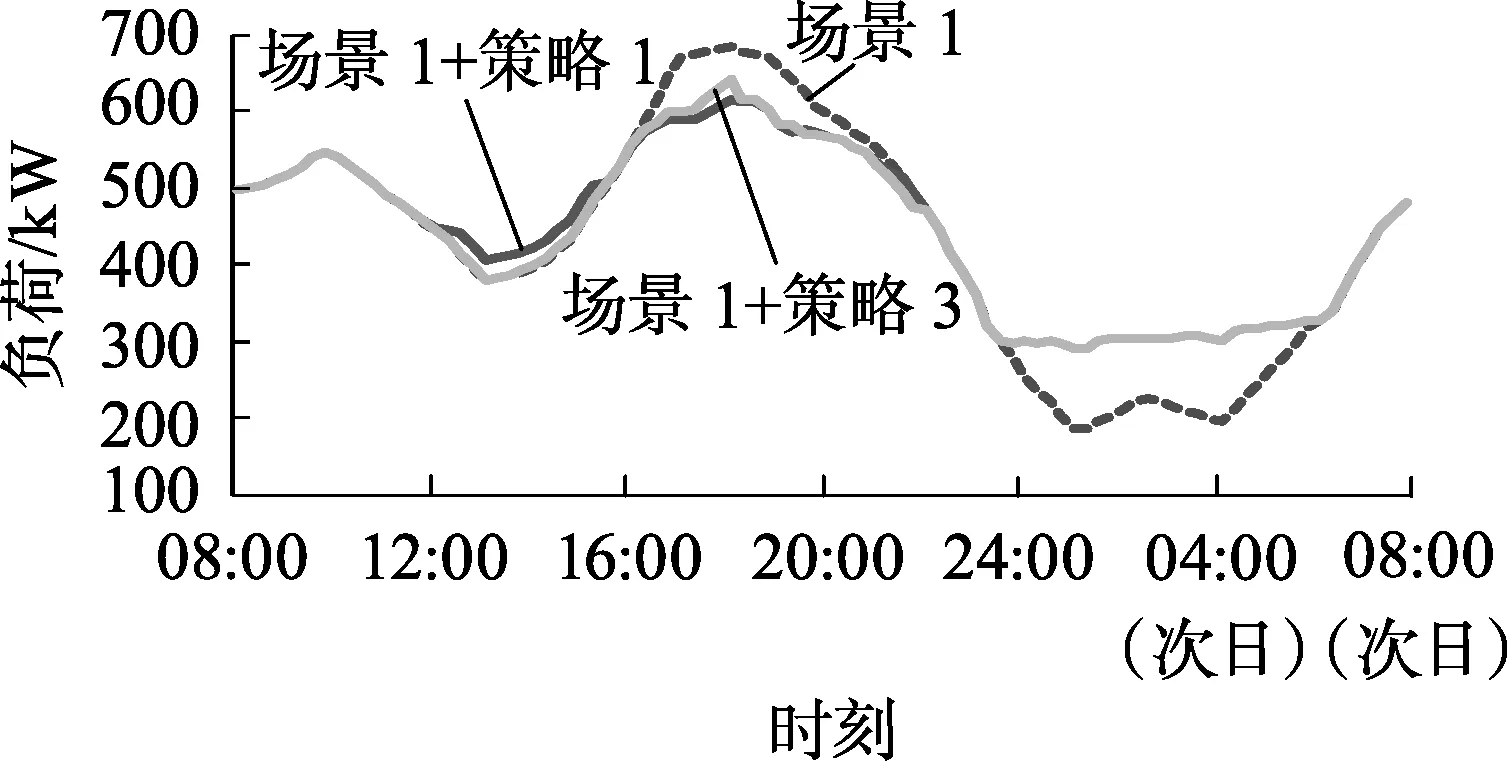
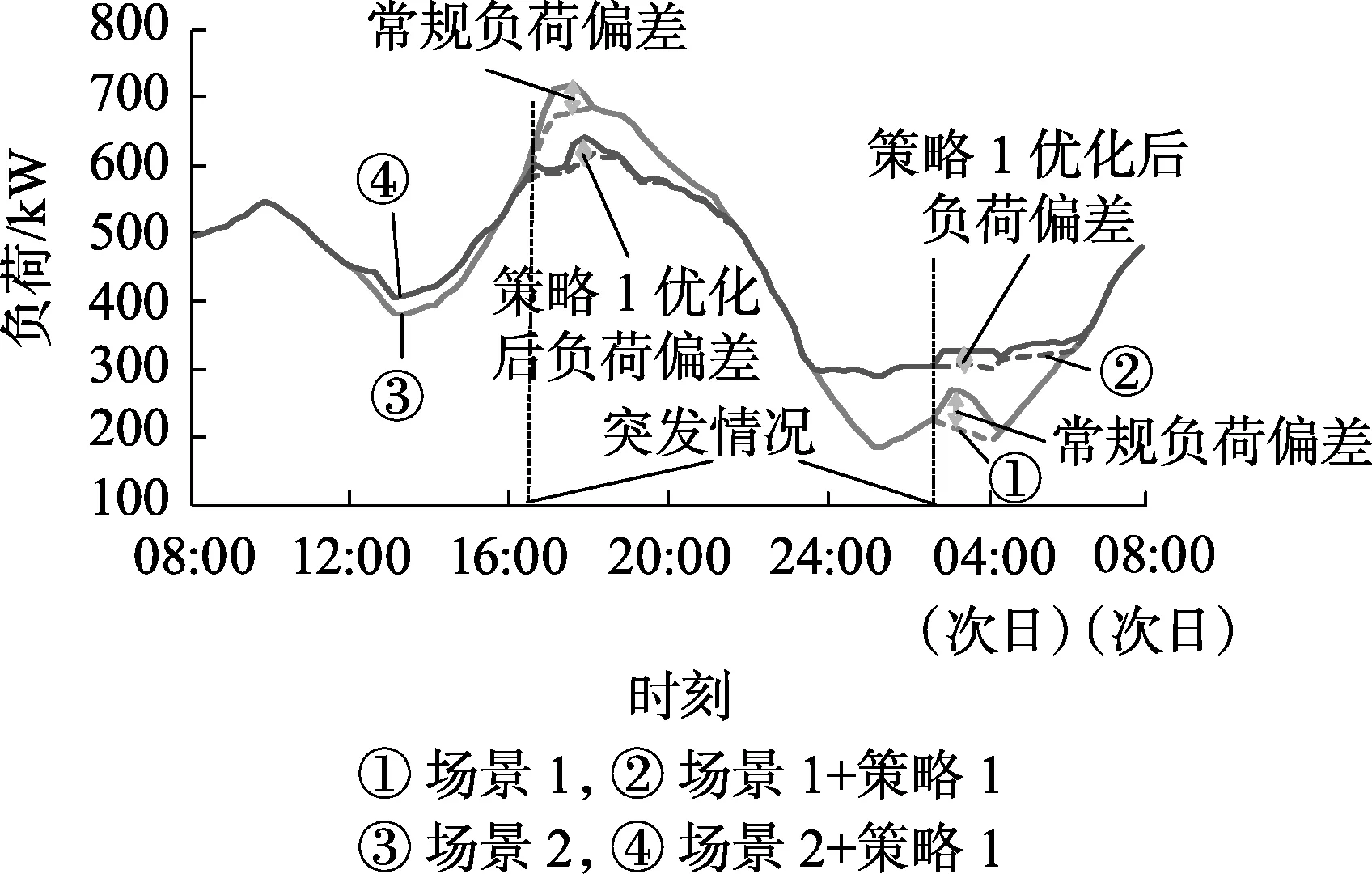
-Pdc,avgηdc,avgNk (11) 其中,PEV,k为时段k内EV总的充放电功率;Pc,avg和Pdc,avg分别为该区域EV的平均充电功率和平均放电功率;ηdc,avg为该区域EV的平均放电效率;Nk为时段k预计可受调度的EV数量,可采用文献[16]的方法基于相似日相同时段历史数据进行预测。 式(11)是对未来各个时段EV总的充放电功率进行约束。由于未来EV到达或驶离充电站的信息无法提前准确获得,需要根据历史数据进行预测。 c. 时段t+1—T1+λT2内EV总的充电功率之和约束和总的放电功率之和约束。 (12) (13) (14) (15) 未来各时段内EV总的充电功率之和与总的放电功率之和受当前时段接入系统的EV总的充放电能力约束。增加该约束可帮助调度机构尽可能地将充电负荷安排在负荷低谷时段和将放电出力安排在负荷高峰时段。 在第一步优化得到当前时段EV总的充放电功率后,下一步的工作是求取满足第一步所求得的EV总的充放电功率要求的充放电调度计划。本节以未参与充放电EV的可转移充放电量裕度最大为目标,使得在调度相同数量EV充放电的情况下,后续时段的EV可转移充放电量裕度最大,从而能够更好地应对负荷预测偏差和EV充放电的随机性等不确定性因素对EV充放电调度的负面影响。该优化问题的目标函数可表示为: (16) 求取时段t的充放电调度计划需满足如下约束条件。 a. 时段t内EV总的充放电功率实际值约束。 (17) (18) b. EV电池的SOC等式约束。 (19) c. 电池电量安全约束。 (20) 其中,Smin和Smax分别为EV电池的SOC下限和上限。 d. EV不可参与充放电的条件约束。 (21) (22) e. 电池充放电互斥性约束。 (23) 第一步中EV总的充放电功率实时优化模型为二次规划问题,第二步中EV充放电调度计划优化模型属于0-1整数规划问题。这2个优化模型均可采用商业求解器求解。YALMIP是一个基于MATLAB仿真平台的建模和优化工具箱,可调用外部求解器(如CPLEX、GUROBI、IPOPT等)对优化问题进行求解[17]。本文基于MATLAB平台进行建模,并通过YALMIP调用外部求解器对所构建的2个优化模型进行求解。针对每个调度时段,根据接入系统的EV信息、系统负荷水平等信息,优化得到EV充放电调度计划。求解流程如图3所示。 图3 EV充放电实时调度模型求解流程Fig.3 Flowchart of solving real-time dispatch model for EV charging/discharging 以一台10kV配电变压器的供电区域为例说明本文所提方法。假设该区域共有100个充电桩,即最多可同时满足100辆EV用电。采用帝豪EV300和江淮iEV6s这2款市场上主流EV车型的电池参数,如表1所示。假设2款车型数量各占一半,电池的SOC随行驶里程呈线性下降关系,且EV采用恒功率充放电。 表1 EV电池参数Table 1 Parameters of EV battery 车主安排EV充放电的行为具有随机性,且车主之间存在个体差异,为了简化起见,以大多数车主的行为为基准模拟EV的充放电行为。本文设定Slow和SV2G均为0.5;对于有充电需求的EV,Sleave设为0.8;对于可提供V2G服务的EV,Sleave设为0.35。在高电价时段,若EV用户当日再无出行需求,则EV充电需求将被转移至低电价时段。 表2 EV的出行数据Table 2 Traveling data of EV 通过对表2中满足不同概率分布的各类数据进行抽样,可模拟EV用户上班和下班的出发与到达时刻、EV到达充电站时电池的SOC及离开充电站时电池可达到的SOC等数据。 设置2种负荷曲线场景,比较所提实时充放电调度策略(策略1)和另外2种策略(策略2和策略3),以验证所提策略的有效性。 场景1:理想情形,实际负荷与预测负荷一致。 策略1:采用分段削峰填谷方式,在每个时段优化EV总的充放电功率后,以未参与充放电的EV可转移充放电量裕度最大为目标求取充放电调度计划。 策略2:采用分段削峰填谷方式,在每个时段优化EV总的充放电功率后,通过随机选取EV参与充放电来确定充放电调度计划。 策略3:未采用分段削峰填谷方式,而在每个时段优化EV总的充放电功率后,以未参与充放电的EV可转移充放电量裕度最大为目标求取充放电调度计划。 针对上述2种场景和3种调度策略的不同组合进行了仿真计算,结果如表3所示。 表3 场景1和场景2采用不同调度策略所得负荷相关参数比较 有问题有问题有问题场景和策略调度时间区间1调度时间区间2峰谷差/kW峰谷差减小程度/%方差/kW2方差减小程度/%峰谷差/kW峰谷差减小程度/%方差/kW2方差减小程度/%场景1304084910294.7088870场景1+策略121030.9366456.8189.035.7328063.1场景1+策略222924.7388554.2192.434.7347060.9场景1+策略326014.5512039.7189.035.7328063.1场景2339095210294.7080490场景2+策略123431.0417956.1189.035.9300462.7场景2+策略225225.7435854.2192.434.7335058.4 图4 场景1采用策略1和2得到的优化结果对比Fig.4 Optimization result comparison when Scenario 1 adopts Strategy 1 and 2 场景2采用策略1和策略2得到的优化结果对比如图5所示。从图5和表3可看出:在负荷预测存在较大偏差时,策略1较策略2能更好地改善负荷轮廓。 图5 场景2采用策略1和2得到的负荷曲线对比Fig.5 Load curve comparison when Scenario 2 adopts Strategy 1 and 2 因此,以未参与充放电的EV可转移充放电量裕度最大为目标求取充放电调度计划,可使得后续时段EV充放电量的调度灵活性最大,从而能够更好地改善负荷轮廓。 场景1采用策略1与策略3所得到的优化结果对比如图6所示。策略1与策略3这2种策略的区别在于是否采用分段削峰填谷方式。从图6和表3可以看出:在调度时间区间1中,策略1得到的优化结果的峰谷差减小程度与方差减小程度2项指标均明显优于策略3;在调度时间区间2中,两者得到的优化结果基本相同。采用策略3时,为了使系统总负荷水平的方差最小,将高电价时段产生的充电需求转移至负荷水平较低的低电价时段予以满足。但是,由于充放电量只能针对EV停留在充电站的时间段内进行转移,因此上述安排在实际调度中无法实现,从而导致在高电价时段的负荷低谷期间未及时安排有充电需求的EV充电。调度时间区间2属于调度周期的后半段,由于采用实时调度策略,调度周期后半段的调度结果不受是否采用分段削峰填谷方式所影响。 图6 场景1采用策略1与3得到的优化结果对比Fig.6 Optimization result comparison when Scenario 1 adopts Strategy 1 and 3 因此,分段削峰填谷能够有效地适应EV充放电量可转移区间限制以及高、低电价时段负荷水平相差较大的特点,从而能够更有效地改善负荷轮廓。 图7 场景1与场景2采用策略1得到的优化结果对比Fig.7 Optimization result comparison when Scenario 1 and 2 adopt Strategy 1 因此,采用策略1时调度结果能够及时地响应负荷曲线的突然波动,根据实际情况及时更新充放电调度方案,大幅削减负荷波动偏差,并平稳消纳突然波动的负荷。 针对EV充放电所具有的灵活性,本文首先提出了可转移充放电量裕度的概念,在此基础上发展了计及可转移充放电量裕度的EV充放电实时调度模型。通过算例分析,得到如下结论: a. 所提EV充放电调度策略能够在满足EV出行需求的前提下,充分利用充放电量的可转移特性,及时响应负荷波动,实时更新调度计划; b. 在针对每个时段优化得到EV总的充放电功率后,以未参与充放电的EV可转移充放电量裕度最大为目标求取充放电调度计划,可使得下一时段EV充放电量的调度灵活性最大,从而能够更好地应对负荷预测偏差与EV充放电的随机性; c. 分段削峰填谷策略能够有效地适应EV充放电量可转移区间的限制以及高、低电价时段负荷水平相差较大的特点。 综上,所提EV充放电调度策略和相关措施能够有效地改善负荷曲线轮廓。 在后续研究工作中,笔者将扩展本文所构造的优化模型,进一步考虑电力网络约束和EV提供调频、旋转备用等辅助服务的情形。 参考文献: [1] 中华人民共和国国务院. 节能与新能源汽车产业发展规划(2012—2020年)[EB/OL]. (2012-06-28)[2017-01-28]. http:∥www.gov.cn/zwgk/2012-07/09/content_2179032.htm. [2] CLEMENT-NYNS K,HAESEN E,DRIESEN J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid[J]. IEEE Transactions on Power Systems,2008,25(1):371-380. [3] 赵俊华,文福拴,杨爱民,等. 电动汽车对电力系统的影响及其调度与控制问题[J]. 电力系统自动化,2011,35(14):2-10. ZHAO Junhua,WEN Fushuan,YANG Aimin,et al. Impact of electric vehicles on power systems as well as the associated dispatching and control problem[J]. Automation of Electric Power Systems,2011,35(14):2-10. [4] 王建,吴奎华,刘志珍,等. 电动汽车充电对配电网负荷的影响及有序控制研究[J]. 电力自动化设备,2013,33(8):47-52. WANG Jian,WU Kuihua,LIU Zhizhen,et al. Impact of electric vehicle charging on distribution network load and coordinated control[J]. Electric Power Automation Equipment,2013,33(8):47-52. [5] 姚伟锋,赵俊华,文福拴,等. 集中充电模式下的电动汽车调频策略[J]. 电力系统自动化,2014,38(9):69-76. YAO Weifeng,ZHAO Junhua,WEN Fushuan,et al. Frequency re-gulation strategy for electric vehicles with centralized charging[J]. Automation of Electric Power Systems,2014,38(9):69-76. [6] 武小梅,谢旭泉,林翔,等. 电动汽车提供备用服务的地区电力市场模型[J]. 电力系统自动化,2016,40(24):71-76. WU Xiaomei,XIE Xuquan,LIN Xiang,et al. Local electricity market model considering reserve service provided by electric vehicles[J]. Automation of Electric Power Systems,2016,40(24):71-76. [7] TAN Z,YANG P,NEHORAI A. An optimal and distributed demand response strategy with electric vehicles in the smart grid[J]. IEEE Transactions on Smart Grid,2014,5(2):861-869. [8] 孙晓明,王玮,苏粟,等. 基于分时电价的电动汽车有序充电控制策略设计[J]. 电力系统自动化,2013,37(1):191-195. SUN Xiaoming,WANG Wei,SU Su,et al. Coordinated charging strategy for electric vehicles based on TOU price[J]. Automation of Electric Power Systems,2013,37(1):191-195. [9] 徐智威,胡泽春,宋永华,等. 基于动态分时电价的电动汽车充电站有序充电策略[J]. 中国电机工程学报,2014,34(22):3638-3646. XU Zhiwei,HU Zechun,SONG Yonghua,et al. Coordinated charging strategy for PEV charging stations based on dynamic time-of-use tariffs[J]. Proceedings of the CSEE,2014,34(22):3638-3646. [10] 王姝凝,杨少兵. 居民小区电动汽车充电负荷有序控制策略[J]. 电力系统自动化,2016,40(4):71-77. WANG Shuning,YANG Shaobing. A coordinated charging control strategy for electric vehicles charging load in residential area[J]. Automation of Electric Power Systems,2016,40(4):71-77. [11] 姚伟锋,赵俊华,文福拴,等. 基于双层优化的电动汽车充放电调度策略[J]. 电力系统自动化,2012,36(11):30-37. YAO Weifeng,ZHAO Junhua,WEN Fushuan,et al. A charging and discharging dispatching strategy for electric vehicles based on bi-level optimization[J]. Automation of Electric Power Systems,2012,36(11):30-37. [12] 项顶,宋永华,胡泽春,等. 电动汽车参与V2G的最优峰谷电价研究[J]. 中国电机工程学报,2013,33(31):15-25. XIANG Ding,SONG Yonghua,HU Zechun,et al.Research on optimal time of use price for electric vehicle participating V2G[J]. Proceedings of the CSEE,2013,33(31):15-25. [13] 曹一家,刘易珠,阙凌燕,等. 换电站与电网协调的多目标双层实时充放电调度方法[J]. 电力自动化设备,2015,35(4):1-7. CAO Yijia,LIU Yizhu,QUE Lingyan,et al. Multi-objective bi-level real-time charging/discharging dispatch with coordination of BSS and grid[J]. Electric Power Automation Equipment,2015,35(4):1-7. [14] GAN L,TOPCU U,LOW S H. Optimal decentralized protocol for electric vehicle charging[J]. IEEE Transactions on Power Systems,2013,28(2):5798-5804. [15] 畅广辉,刘涤尘,熊浩. 基于多分辨率SVM回归估计的短期负荷预测[J]. 电力系统自动化,2007,31(9):37-41. CHANG Guanghui,LIU Dichen,XIONG Hao. Short term load forecasting based on multi-resolution SVM regression[J]. Automation of Electric Power Systems,2007,31(9):37-41. [16] 叶林,陈政,赵永宁,等. 基于遗传算法-模糊径向基神经网络的光伏发电功率预测模型[J]. 电力系统自动化,2015,39(16):16-22. YE Lin,CHEN Zheng,ZHAO Yongning,et al. Photovoltaic power forecasting model based on genetic algorithm and fuzzy radial basis function neural network[J]. Automation of Electric Power Systems,2015,39(16):16-22. [17] LOFBERG J. YALMIP:a toolbox for modeling and optimization in MATLAB[J]. Optimization,2004,41(3):284-289. [18] 田立亭,史双龙,贾卓. 电动汽车充电功率需求的统计学建模方法[J]. 电网技术,2010,34(11):126-130. TIAN Liting,SHI Shuanglong,JIA Zhuo. A statistical model for charging power demand of electric vehicles[J]. Power System Technology,2010,34(11):126-130. [19] 北京交通发展研究中心. 2015年北京交通发展年报[EB/OL].(2016-03-03)[2016-11-22]. http:∥www.bjtrc.org.cn/InfoCenter/NewsAttach/2015年北京交通发展年报_201603031431 17631.pdf.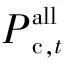
2.2 EV充放电调度计划优化
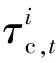

2.3 两步优化模型的求解方法及流程

3 算例分析

Table 3 Load parameter comparison when Scenario 1 and 2 adopt different dispatch strategies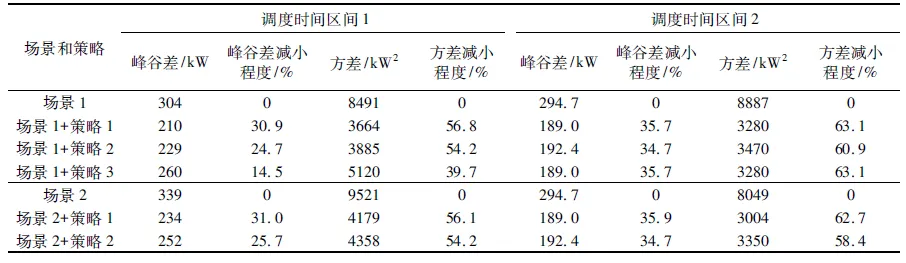



4 结论

