节点分区与平均跳数加权的三维DV-Hop定位算法
张伯泉,王瑞成
广东工业大学 计算机学院,广州 510006
1 引言
随着无线通信技术的快速发展,无线传感器网络的应用越来越广。在诸多应用中需要确定网络节点的位置。因此,无线传感器网络的定位技术受到广泛关注,成为研究热点。对于平面布局的无线传感器网络定位需要二维定位研究,对于空间布局的无线传感器网络定位需要三维定位研究。相对于二维定位,三维定位技术应用更加广泛。因此,三维定位方法的研究更加热门[1-3]。
三维定位算法研究中有基于测距与非测距这两种定位算法。基于测距定位算法研究的有RSSI、TOA、TDOA、AOA等[4-6]。但由于功耗、成本等方面原因,非测距定位算法更受关注。DV-Hop(Distance Vector Hop)是典型的非测距定位算法,但存在定位精度不高的缺陷。文献[7]提出了坐标四面体质心定位算法,但是它没有考虑未知节点不在某个四面体内的情况。文献[8]提出了基于平均跳距修正的三维DV-Hop定位算法,但它需要实际距离与估计距离的差值,而差值的准确性有待提高。文献[9]提出了一种分区的三维DV-Hop定位改进算法,提高了锚节点间跳数准确度,但没有研究不同跳数对于定位的影响。文献[10]提出一种跳数加权三维定位改进算法,一定程度上降低了定位的平均误差。文献[11]提出了一种基于初始位置投影矫正的三维定位算法,但是在实际情况中山体不能简单地用某一条抛物面来模拟。文献[12]提出了一种细化节点跳数的多通信半径加权的DV-Hop改进算法,但是该算法在传感器的能源消耗和时间效率上有一定缺陷。文献[13]提出最小跳数偏离度的概念,并对未知节点的定位进行了修正。但是当节点的布局改变时,算法的因子调整需要进行试验后进行调整,适用性受到限制。本文在前人研究的基础上提出一种基于分区与跳数加权相结合的三维定位算法。它对无线传感器网进行分区以提高跳数估计的准确性,又考虑不同跳数对于定位误差的影响,对锚节点跳数进行加权处理,能够有效降低网络定位误差。
2 三维DV-Hop定位算法
三维DV-Hop定位算法是对二维DV-Hop定位算法的扩展,是一种基于距离矢量无需测距定位算法[14-15]。DV-Hop算法的基本思想是将未知节点到信标节点之间的距离用平均跳距和两者之间跳数的乘积表示,跳数计算方式是锚节点通过洪泛的方式向整个网络传播位置信息和跳数信息,其中信息发起的锚节点的跳数定义为0,当最近的节点收到此锚节点发出的信息时把跳数加1,并传给下一个节点。当一个节点收到多个跳数信息时,进行比较,取所有跳数的最小值。其定位过程如下:
(1)计算节点间最小跳数。即确定锚节点与在通信范围内的未知节点间最小跳距,即两个节点间的距离小于通信。
(2)计算未知节点与锚节点间的距离。根据位置坐标信息和步骤(1)记录的跳数,通过式(1)估算平均跳距:

式中(xi,yi,zi)和(xj,yj,zj)为锚节点i和 j的坐标,hij是锚节点i到锚节点 j的跳数,Hopsizei表示锚节点i的平均跳距。每个未知节点利用自己的平均跳距和到各个锚节点的最小跳数的乘积,近似得到其与每个锚节点的距离。
(3)利用三边测量法或极大似然法计算未知节点的坐标。
3 改进的三维DV-Hop定位算法
经典DV-Hop定位算法既忽略了未知节点与锚节点间相同跳数、不同距离的情况,也没有考虑多跳情形对平均跳距的影响。节点间跳距的计算是基于锚节点通信的直线距离,没有考虑常见的多跳折线的情况以及相同跳数时距离不同的情况,如图1所示。定位误差将随着节点间的跳距的增加而增大。
中国在全面建设和完善社会主义市场经济的进程中,陌生人间的交往已取代熟人间的交往而成为主导性和常态化的交往模式,于是在家庭和国家之间形成了一个由陌生人构成的庞大复杂的公共交往空间。相应地,家庭和国家对个体或组织的影响力、规范力都有所削弱,这就决定了传统的以熟人共同体为背景的修齐治平的道德责任必须突破血缘和地缘的狭隘语境,经过思想内容的更新和创新才可能对以市场社会为背景的陌生人社会有规范意义。
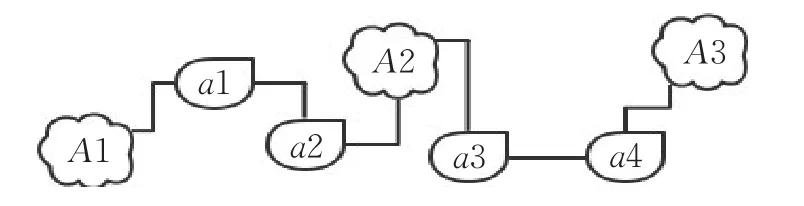
图1 无线传感器网络节点
图中,A1、A2、A3为锚节点,a1、a2、a3、a4为未知节点。由图中可知,A1到A2与A2到A3的跳数都为2,但是实际距离并不相同。
针对这两种情况本文提出一种3DPHW-DVHop改进定位算法。算法描述如下:
(1)计算锚节点坐标的几何中心:

(2)计算锚节点三维坐标中每一维度的方差:

(3)以最大的两个维度方差为根据对无线传感器网络进行区域划分区域划分为正方形,区域的个数:

其中L和W分别为一个特定的目标区域的长度和宽度,R为传感器的通信半径,以R为长的正方形的外接圆直径为 2R,设K为划分系数,其值取决于锚节点的实际相对密度。因此,正方形的长度的设定为 2RK。
(4)以经典DV-Hop算法中的方法计算各分区后锚节点间的跳数及每个锚节点的平均跳距,锚节点间的平均跳距表达式如下:

(5)基于跳距加权的未知节点与锚节点间的距离计算。定位实践表明,锚节点间的跳数越少,定位误差越小。因而越小的跳数对锚节点间平均跳距影响越大,所以跳距越小赋予的权值应当越大。权值采用的表达式如下:

(6)由步骤(1)到(5)可计算出划分区域后每个分区内的平均节点跳距,本文算法采用的平均跳距表达式如式(11)所示:
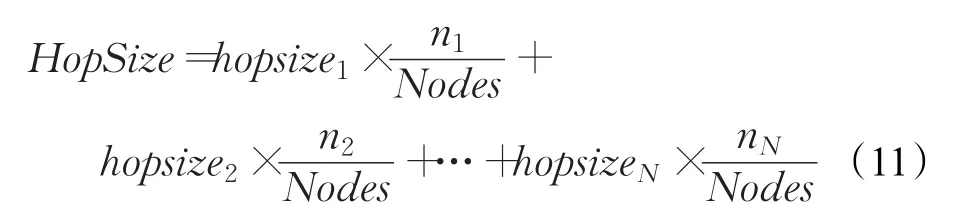
其中hopsize1到hopsizeN为节点分区后计算得出的区域平均跳距,n1到nN为每个分区后区域内的节点个数,Nodes为实验节点总数。
(7)计算未知节点到锚节点的距离极大似然法公式如下:

4 算法仿真及结果分析
采用Matlab对本文算法进行仿真,并与3D-DVHop基本算法、3D-WD-DVHop算法以及3DPH-DVHop算法比较。无线传感器网络的三维布局设为100 m×100 m×100 m的正立方体,随机产生100个网络节点。实验以锚节点数和锚节点通信半径为变量验证算法的平均定位误差。
图2为三维节点随机分布图,其中红色节点为锚节点,蓝色节点为未知节点。
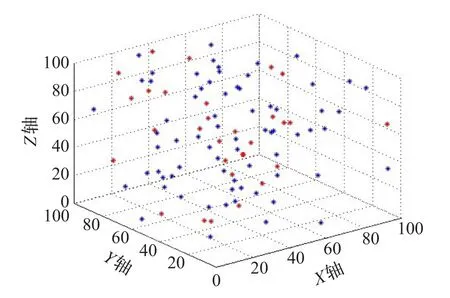
图2 无线传感器网络节点三维随机布局
网络平均定位误差计算公式(12)如下:
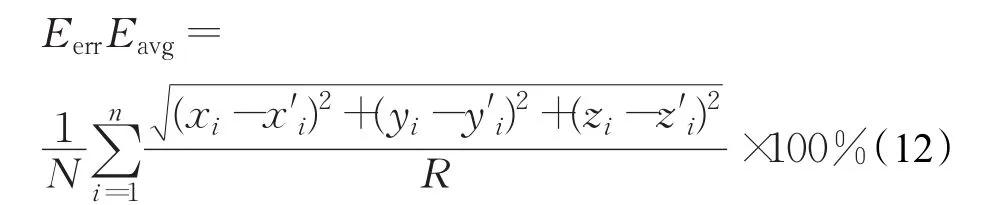
式中,(xi,yi,zi)为未知节点 i的实际坐标,(x′i,y′i,z′i)为算法求出的未知节点的估计坐标,R为锚节点的通信半径,N为未知节点的总数。
4.1 锚节点数对定位误差的影响实验
图3节点总数为100,通信半径为30 m。锚节点从10增加到40过程中,实验300次得出平均网络定位误差的影响。图3即为本文算法3DPHW-DVHop与基于加权的三维DV-Hop定位算法以及3DPH-DVHop定位算法网络平均定位误差的对比图。

图3 锚节点数目与定位误差的关系
从图3中可以看出当锚节点为10时,3DPH-DVHop定位算法相比3D-WD-DVHop定位算法平均定位误差小4%左右,本文算法3DPHW-DVHop低于3D-WD-DVHop算法5%。说明在锚节点比例较小时,分区定位算法优势较为明显,当锚节点比例达到20%,3DPH-DVHop算法与3D-WD-DVHop定位算法的平均定位误差相对持平,而本文算法定位误差明显优于这两种算法。这是因为当锚节点个数较少时,纯粹基于分区算法忽略了区域节点个数占总节点数的比重,因而在计算节点平均跳距时容易产生偶然性误差,同时也没有考虑相同跳数情况下节点实际距离不同的情况,而本文算法则综合考虑了这两个因素,同时对区域划分后求出的平均跳距进行了进一步的加权求值处理。基于节点加权的算法则是因为锚节点个数较少,在计算未知节点与锚节点的跳数时,容易产生较大误差。
图4节点总数为100,通信半径为40 m。锚节点从10到40过程中,锚节点个数与定位误差的关系。
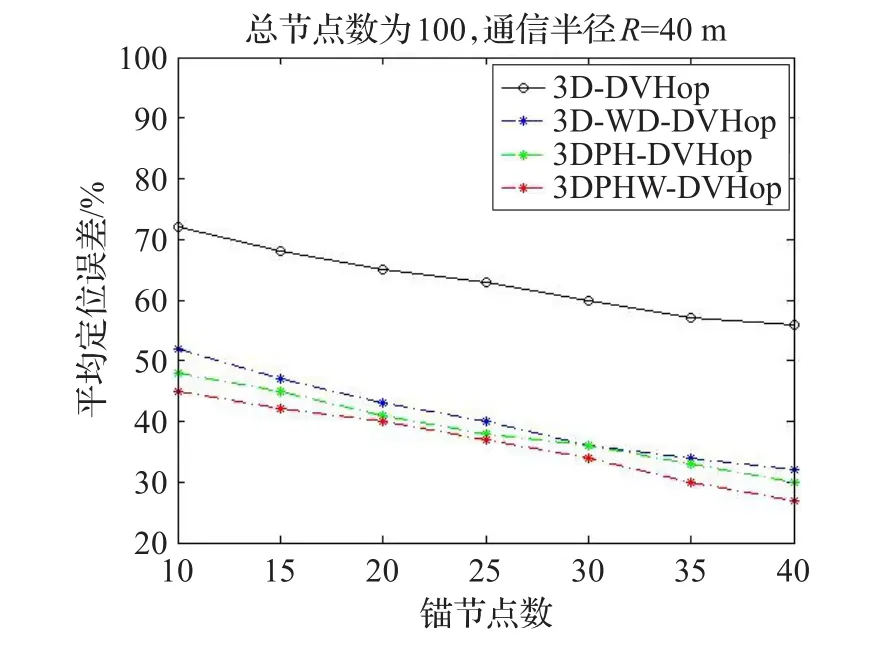
图4 锚节点个数与定位误差的关系
图4所示与图3相比,当锚节点为10的时候,本文算法的平均网络误差为45%,低于通行半径为30 m时10%,当随着锚节点数增加时,误差率也是随之减小,当锚节点增加到40时,网络平均定位误差为27%左右,低于3DPH-DVHop算法与3D-WD-DVHop定位算法3%~4%,而三种算法之间的定位误差率相对于半径为30 m,定位误差相差减小,这是因为通信半径增加,节点间的跳数总和会随之减小,节点间的平均跳数减小,根据式(12)可知定位误差也会随着减小。当锚节点逐渐增多时,因本文算法相对与分区算法考虑了每个分区节点数占总节点数的比重,并对节点跳距进行的加权求值,避免了偶然性误差,提高了定位的精确度。
图5节点总数为100,通信半径为40 m。锚节点从比例保持30%时,节点个数与定位误差的关系。

图5 节点个数与定位误差的关系
从图中可以得出,当锚节点数一定时,随着通信半径的增加,三种定位算法的网络平均误差逐渐减小,其中本文算法在半径20 m到35 m时,本文算法的平均定位误差明显小于3DPH-DVHop算法和3D-DW-DVHop算法,其中主要原因归于区域划分后,局部节点间的跳数计算更加精确,节点平均跳距再采用跳数加权处理和区域节点平均跳距值加权处理后,局部节点定位的精确度也得到了提升。
4.2 算法综合性能比较分析
4.2.1 时间复杂度
由前文算法描述可知,本文算法和3DPH-DVHop算法,在对选取(x,y,z)作为区域划分的参考时,分别对每一个维度进行了求方差,时间复杂度为O(n);在对节点坐标进行划分分区时要计算节点所属的区域,时间复杂度也为O(n),相对于3D-WD-DVHop和普通3DDVHop算法多耗时O(n),其中n为节点个数。接下来在求节点的权重时,以及最后的定位过程中时间复杂度与其他算法基本相同,而综合整个3D-DVHop定位算法,时间复杂度为O(n2)。因此,本文算法相对于3DWD-DVHop和普通3D-DVHop算法多消耗的O(n)时间可以忽略不计。
4.2.2 空间复杂度
基于分区的3D-DVHop定位算法,在对节点进行划分时,需要对每个节点所属分区进行记录,因而相对于3D-DVHop算法和3D-DW-DVHop算法多占用了O(n)的存储空间,其中n为实验中的节点总数。
综上所述,本文算法比其他算法略优,一是对区域节点进行了权值处理,二是多占用了O(n)的存储空间;而时间复杂度与其他算法基本一致。
5 结论
基于区域划分的加权三维定位算法,利用节点分区减小了因区域过大造成节点跳数偏大的偶然性误差,同时节约了节点的能源消耗,然后通过节点跳距加权的方式,考虑了因节点跳数不同时,节点在定位过程中占的比重是不同的,因为在理论上,当节点间的跳数都为1时,定位精度最高。通过理论分析和实验仿真证明,在锚节点比例较小时和节点通信距离较小时,节点平均定位误差明显好于其他三维定位算法,同时随着锚节点数增加和通信距离增大时,本文算法的定位误差率也稍微好于3DPH-DVHop算法和3D-DW-DVHop算法,在室外的三维定位中更具有实际应用效果。不足之处在于分区的节点跳数只是基于局部最优的节点定位算法,不是基于全局最优的定位算法。
[1]Savvides A,Han C C,Srivastava M B.Dynamic finegrained localization in ad-hoc networks of sensors[C]//Proceeding of the 7th Annual International Conference on Mobile Computing and Networking,Rome,2001:166-179.
[2]Niculescu D,Nath B.Ad hoc positioning systems(APS)using AO-A[C]//Proceeding of the 22nd Annual Joint Conference of the IEEE Computer and Communications,San Francisco,2001:1734-1743.
[3]Wang Jing,Ghosh R K,Sajal K Das.A survey on sensor localization[J].Journal of Control Theory and Applications,2010,27(4):1345-1352.
[4]Zhang Zhibin,Xu Xiaoling,Yan Lianlong.Underground localization algorithm of wireless sensor network based on Zigbee[J].Journal of China Coal Society,2009,34(1):125-128.
[5]戴晨冲,宋来亮,晁代宏.基于四节点RSSI的三维空间定位算法[J].计算机测量与控制,2016,24(1):229-232.
[6]陈庆章,毛科技,何文秀,等.基于共面度和分层结构的WSN三维定位算法[J].电子测量与仪器学报,2012,26(8):673-680.
[7]Chen Hongyang,Huang Pei,Martins M.Novel centroid localization algorithm for three dimensionalwireless sensor networks[C]//4th International Conference on Wireless Communications,Networking and Mobile Computing(WiCOM’08),2008:1-4.
[8]基于平均跳距修正的三维DV-Hop定位算法研究[J].无线通信技术,2013,1:50-53.
[9]Wang Ruijin,Qin Zhiguang,Wang Jahao.A new 3D positioning algorithm using partial hopsize in WSN[C]//International Conference on Communications,2014:91-95.
[10]李琳,赵可,林志贵,等.基于加权的三维DV-Hop定位算法[J].控制工程,2015,22(4):761-764.
[11]胡中栋,肖华为.适应山头地形的无线传感器网络节点定位算法[J].计算机工程与应用,2016,52(10):104-107.
[12]刘士兴,黄俊杰,刘宏银,等.基于多通信半径的加权DVHop定位算法[J].传感技术学报,2015,28(6):883-887.
[13]刘玉珍,王兆丰.基于DV-HOP改进的无线网络定位算法[J].计算机工程与应用,2016,52(4):79-83.
[14]王新生,赵衍静,李海涛.基于DV-HOP定位算法的改进研究[J].计算机科学,2011,38(2):76-78.
[15]刘少强,庞新苗,樊晓平,等.一种有效提高节点定位精度的改进 DV-HOP算法[J].传感技术学报,2010,23(8):1179-1183.

