项目组合交互风险的网络聚类及协同演化研究
赵 静,郭 鹏,王景玫
西北工业大学 管理学院,西安 710072
1 引言
随着经济全球化以及市场竞争的不断加剧,并行开展多个项目已经成为一种常见行为,项目组合呈现出与资本组合同等重要的地位[1],而风险又是项目组合管理不可回避的基本问题。组合一词来源于“不要把所有的鸡蛋放在一个篮子里”的风险分散和规避的理念,以资本资产组合为代表的主流风险理论成果大多来自于标准金融范畴,如以MV模型为基础的VaR、均值半方差和均值-Gini系数模型和以信息熵、模糊数或实物期权为基础的风险不确定性模型等[2-3],然而一致性风险测度公理的提出使大家意识到目前的风险度量方法其结果与客观风险之间存在着较大差距[4-5]。究其原因,一方面,实体项目尤其是以R&D为代表的项目组合属于高风险且与管理相结合的投资行为,其不可分割性、规模性和持续性导致资本组合领域的风险分析方法在项目组合风险管理中的应用效果不佳[6-7];另一方面,资本组合的风险分散和规避策略通过项目差异化来降低组合风险,但是这种差异化的效应在项目组合研究中并不明确且未被深入讨论,在解释单项目风险到项目组合风险的传递和作用机制问题上显得乏力。
事实上,项目组合风险包含大量的风险决策信息以及各种信息的非对称作用,是一个典型的复杂系统。就其构成而言,既有来自单项目的风险,也有因项目间属性多源性和冲突性导致的交互作用风险。因此,项目组合风险研究需要分析多个项目构成一个整体的组合效应,探讨复杂风险属性的交互作用机制。正如学者们指出的,基于后果与概率的风险测度方法不能全面刻画风险,还需要考虑不同单元或子系统间的依赖性,从一般意义上开展项目组合风险与单个项目风险之间的关系研究具有重要意义[8-9]。
本研究借助网络这一研究复杂对象和解决复杂性问题的有效手段,从项目组合交互关系入手,分析项目组合交互风险的网络结构特征及其协同演化规律。注重以项目组合内在子系统(子项目)及其交互关系为基础,解释单项目到项目组合的风险传递过程所体现的动力学行为,进而分析各种微观机制如何作用于项目组合风险。
2 项目组合交互关系及其复杂性
2.1 项目组合交互关系及其分类
交互关系理论是由Baker和Freeland提出的,他们认为交互关系的存在使得组合中某一项目的成本、收益和成功概率等在很大程度上依赖于另外某一些项目是否被选择[10],同时指出忽视项目间交互关系的项目组合研究模型存在相当大的局限性[11]。随着交互关系逐步被纳入项目组合研究范畴,其影响受到诸多学者的关注,如交互关系对资源分配、成功率和组合收益的影响[12-13],技术类交互关系对R&D和IT类项目组合选择优化的重要性[14-15],项目选择和项目组合总体对交互关系的依赖性[16],同时交互关系也被引入项目组合决策的模糊、不确定研究领域[17-18]。
研究发现,表征项目间复杂交互关系的属性指标众多,如预期收益、原材料、技术、预期客户满意度、资金需求、人员需求等。从来源来看,可分为资源、技术和产出(或收益)等三个方面,其影响表现为正负效应两种[19-20];从产生范式来看,分为同类相关型、非同类相关型和不相关型[21];从可能导致的组合功能来看,文献[22]从生态学视角将其分为竞争型、共生型、偏害/偏利型和中性型等,并以此对其交互效应进行定量度量。

表1 项目组合交互关系及其分类
2.2 项目组合交互关系的网络复杂性
伴随着大量复杂设计、研发和建设项目的涌现,项目间交互关系趋向复杂化,并表现出结构多层级、多单元和多功能以及各种风险信息非对称作用的系统复杂性,导致项目组合呈现为具有交互耦合网路特征的复杂系统。如图1所示,项目组合是由多个子系统(或子项目)构成,子系统间信息传递和集结过程正是通过交互关系链联接起来的,理解项目组合系统复杂性的内涵和产生根源可以从以下几方面。

图1 项目组合交互关系及其网络复杂性
(1)流特征。依据一般系统结构理论的关系流概念,在系统信息输入和系统行为或功能输出之间起决定性作用的是基层次上的关系流集,特别是其中的关系流回路[23-24]。项目组合系统包含大量的关系流,如信息流、物质流、能量流、资金流、人力资源流等,这些关系流及其回路构成了项目组合的关系流网,决定和支配网络的行为或功能。
(2)系统的非线性。经济和管理世界中的不确定、不稳定和无序是内在非线性造成的,项目组合系统非线性的直接体现就是项目组合总体不等于单项目的简单相加[3,22]。项目组合的存在依赖于内外部环境的物质、能量、信息交换,而在与系统环境的反复作用中形成的交互耦合网络结构具有非线性,使得局部的关系流优化不等于整体网络行为和功能的优化。
(3)涌现特性是系统复杂性的直接体现。涌现特性最直观的理解是系统的整体行为不能还原为个体行为,而被大家所广泛接受的基于项目差异化的风险规避策略正是对项目组合系统涌现特征的肯定[22]。项目间属性差异和交互关系是形成项目组合交互耦合网络的直接动力,并决定了项目在因果关系链上的位置和网络的层次性。从系统角度来看,项目组合系统的非线性结构是多重、多向和网络化的且具有反馈和放大机制。
(4)系统适应性造就复杂性。项目组合作为一个开放的、动态的而非传统的机械式确定性变化的系统,其复杂性和自身适应性密切相关[25]。项目主体是具有自身目的性、主动性和适应性的个体,通过与环境的信息交换以及与其他项目的相互作用,形成了“刺激—反应”模型,并构成了系统发展和变革的基本动力。
3 项目组合交互风险的网络聚类识别
在项目组合系统内在交互耦合网络形成过程中,交互关系的非对称性使得不同项目在地位与作用、结构与功能上表现出等级秩序性,因此,如何对项目组合风险尤其是交互风险进行定量化表征与分类成为亟待解决问题。然而,客观世界中某些对象类属划分往往呈现出亦此亦彼的模糊性,而传统的分类方法通常对项目进行硬聚类,即判断某个项目属于或不属于某个项目群,而忽视项目的多样性特征。直觉模糊生态聚类算法的提出以项目间风险属性和交互关系的分类识别为基础,同时考虑到项目间生态依赖关系的特点,对项目组合内在子系统及其交互风险网络结构进行定量识别。算法的具体流程如下:
步骤1项目风险属性的模糊分类与表征。
设Y={Y1,Y2,…,Ym}为项目集,G={g1,g2,…,gn}为风险属性集。按照交互关系的来源(见表1)对项目风险属性进行约简和分类,项目Yi的风险属性可用三维矢量空间表示为Yi={Yi(G1),Yi(G2),Yi(G3)},其中Yi(Gj)(j =1,2,3)分别对应资源、技术和产出/收益属性。此处,引用三角模糊数[26]:

将项目Yi的风险属性指标Yi(Gj)表示为直觉模糊集:

其中,μYi(Gj)和υYi(Gj)分别表示项目Yi对应风险属性子集Gj的隶属度和非隶属度,而πYi(Gj)=1-μYi(Gj)-υYi(Gj)表示其不确定程度。
步骤2建立项目间风险属性的直觉模糊相似度矩阵Z={zij}m×m。
根据项目集Y={Y1,Y2,…,Ym}及其风险属性Yi={Yi(G1),Yi(G2),Yi(G3)}构建项目间风险属性相似度的直觉模糊决策矩阵D,矩阵元素dij为直觉模糊数,如表2所示。

表2 直觉模糊决策矩阵
以此为基础,建立直觉模糊集相似度矩阵Z=,其中

其中,λ、β1、β2、β3为事先确定参数,λ≥1,βi∈[ ]0,1且∑βi=1。
步骤3检验直觉模糊相似度矩阵Z是否为等价矩阵。
对矩阵 Z进行合成运算 Z→Z2→Z4→…→Z2k→…,直到满足Z2l=Z2(l+1),则Z2l即为所求等价矩阵,记为
步骤4建立等价矩阵Z∗的λ截矩阵
对于给定的置信水平 λ,依据公式(3)~(5)计算等价矩阵 Z∗的λ截矩阵,其中
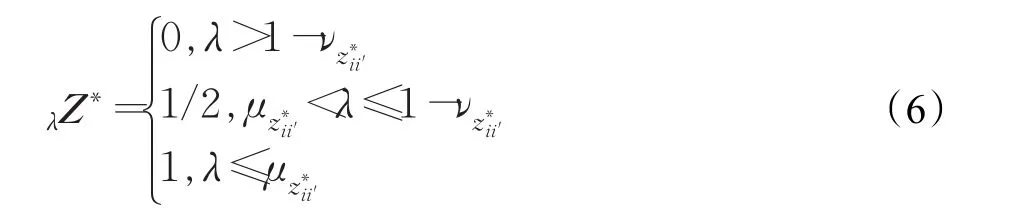
步骤5确定合理的置信水平λ,根据λ截矩阵对项目进行聚类,聚类结果依据项目间风险属性的相似度将项目组合风险系统划分为S(S=1,2,…,l,l≤n)个子系统。从交互关系的产生范式上来看,子系统内项目的风险属性高度相似,归为同类或非同类相关型项目,而不同子系统的项目则归为非同类相关型或不相关型(见表1)。
步骤6子系统内项目风险属性的集成及聚类中心确定。
引入直觉模糊加权几何算子(IFWGw)[28](公式(6))对子系统内项目的风险属性信息进行集成,相应的子系统聚类中心记为Ms,且同样用三维矢量空间Ms={
}
Ms(G1),Ms(G2),Ms(G3)表示,其中Ms(Gj)为直觉模糊数

式中,ω=(ω1,ω2,…,ωn)T为直觉模糊数组Yi(Gj)的指数权重向量,ωi∈[0 ,1]且∑ωi=1。
步骤7构建子系统间风险交互效应的符号判断矩阵。
应用生态学视角下交互关系的功能特征分类,建立子系统间风险交互效应的符号判断矩阵A={αss′(Gjj′)}3j×3j,其中元素 αss′(Gjj′)∈ {- 1,0,1} 表示模块s′的第Gs′为矢量与模块s的第Gs维矢量的风险交互作用关系,分别对应负相关、不相关和正相关。以模块s和模块s′为例,可表示为:
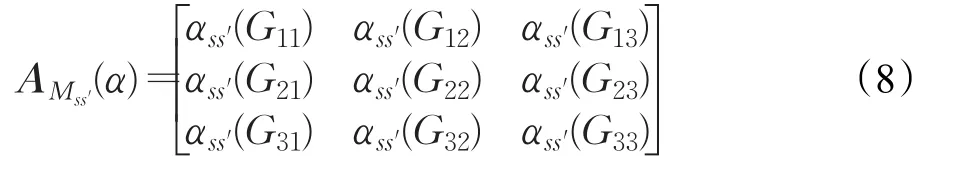
步骤8建立子系统间风险交互效应的模糊生态集成测度模型。
运用直觉模糊数对项目间风险关联测度模型[22]进行扩展,建立具有模糊性和生态依存性的风险交互效应集成测度模型,记为交互风险关联系数。模型构建以Levins生态位重叠理论为基础,强调子系统间风险交互效应的非对称性特征,即,如公式(9)所示:
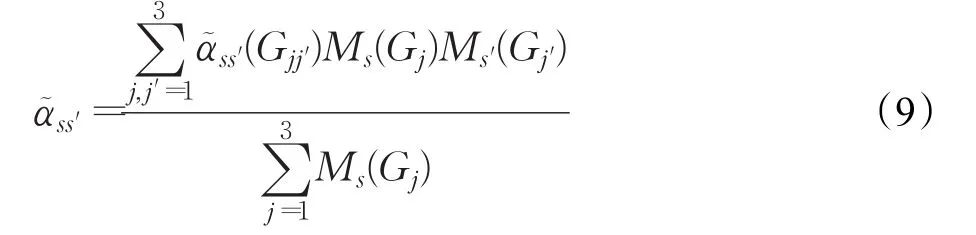
当步骤5中置信水平λ取其下限时,项目组合交互风险聚类结果最大化,即每个项目归为一类,式(9)退化为项目间风险交互关联测度。
4 项目组合交互风险的协同演化模型
4.1 模型构建
风险是项目组合价值的来源,即涉及到威胁也涉及到机会,而项目组合交互风险演化模型的本质是反应其内在结构耦合关系如何作用于组合整体,研究借助非线性动力学方程来刻画项目组合交互风险关系及其动力特征。其中,Logistic和Lotka-Volterra方程被广泛地应用于管理领域,如ICT行业、产业创新、企业联盟等,综合考虑合作与竞争等对系统的影响[29-30]。Lotka-Volterra方程在Logistic方程基础上,一方面反映出系统自适应性和资源环境对其发展的制约,以及系统演化过程中增长和下降的动力机制;另一方面也反映系统内竞争或合作等交互作用关系[31]。
此处,假设子系统Ms在t时刻的收益率用Ns(t)表示,风险通过t时刻Ns(t)的增长率,即dNs(t)/dt来表示。当子系统相对独立且不存在交互作用关系时,Ms的演化过程可借助Logistic方程[32]表示为:
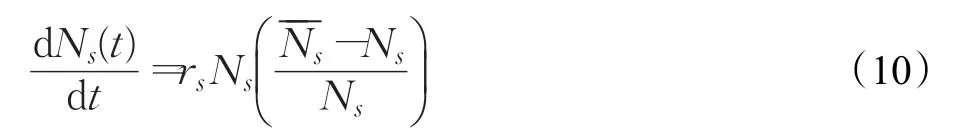
其中,表示在不受限制条件下Ms的最大收益水平,同时,随着t→∞,Ns(t)趋向于饱和水平,收益增长速度趋向于常数rs,即自然增长率;表示t时刻,Ms对自身的阻滞效应。当引入竞争、共生或者偏利偏害项目时,且子系统间存在交互风险效应ass′,则式(10)可修正为Lotka-Volterra模型[32]:

4.2 模型求解与讨论
给定了上述系统(11),此处以两子系统为例分析项目组合交互风险演化过程,相应的系统动力学模型记为:
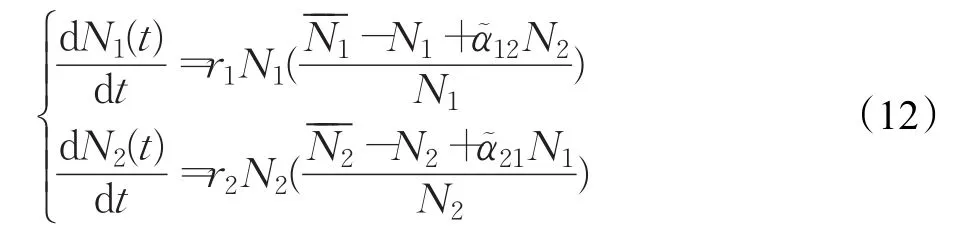
令方程组dN1(t)/dt=0,dN2(t)/dt=0引出平衡条件下的两条直线:

以N1和N2为坐标轴,可以得到方程组的四个定态解:同时,根据模型(12)得到微分方程的特征矩阵:
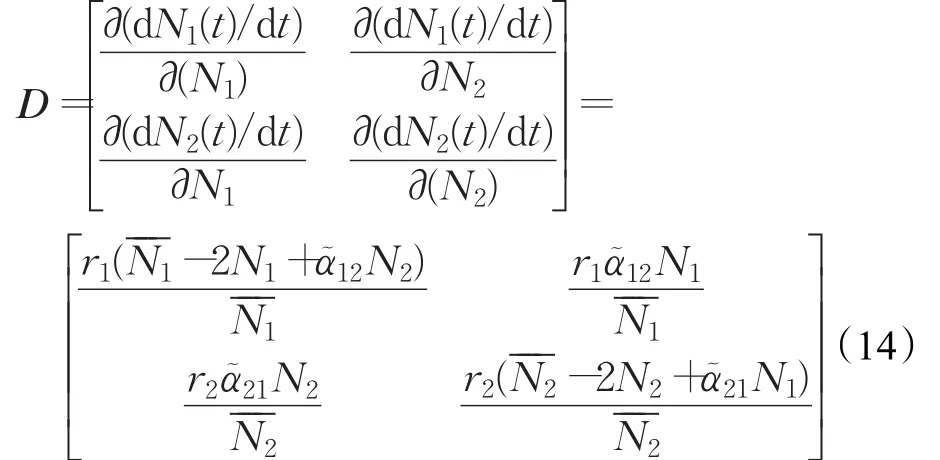
和相应的特征方程为λ2+pλ+q=0,其中:
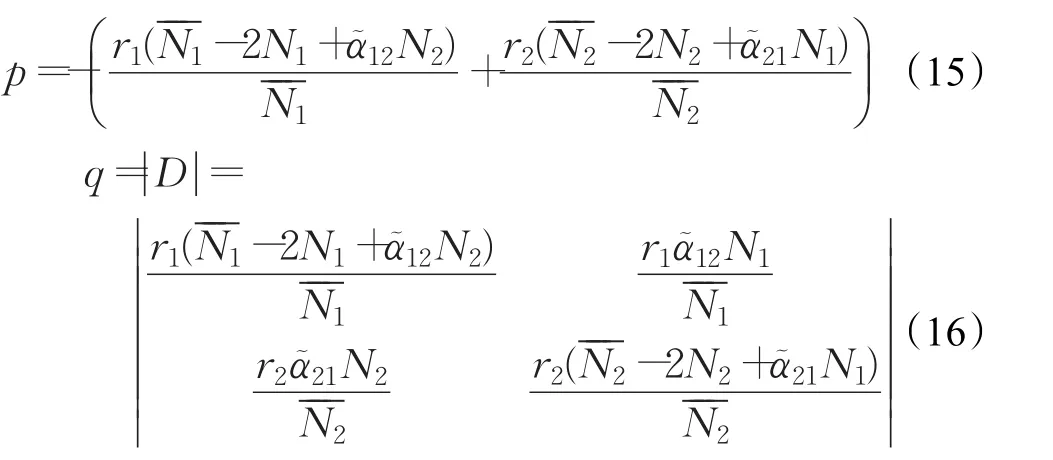
由平衡点稳定理论可知,当时 p>0且q>0时均衡点稳定,而 p<0或q<0是均衡点不稳定。对于经济系统而言,更关心模型(12)正稳定解,即平衡点的存在性。
(1)竞争型演化
当模型(12)中 a12,a21<0 时,N1和 N2呈现竞争关系,根据直线L1和L2的相交情况和轨线走向研究系统的稳定性(如图2),可得:
① 如图2(a),当,式(12)的解有且满足 p>0且q>0,是系统的稳定解,即N1和N2的竞争结果是双方稳定共存。
② 如图2(b),当平衡线L1和L2将平面分为四个区域I、II、III和IV,情况分别如下:若初始值在区域II,式(12)的解有极限N1(t)→0,是系统的稳定解;若初始值在区域III,式(8)的解有极限 N2(t)→0,N1(t)→是系统的稳定解;若初始值在区域I或IV,式(12)有定态解但不满足 p>0且q>0,因此不是系统稳定解,否则方程组的解必进入区域II或III。

图2 竞争型演化
(2)共生型演化
当模型(12)中交互效应系数 a12,a21>0 时,N1和N2呈现共生关系,平衡线L1和L2的相交情况和轨线走向如图3所示。方程组的四个定态解E1(0,0)、E4满足 p>0且q>0,是模型的稳定解,N1和 N2由于资源、技术或是市场的共享和合作而产生了协同发展效应。
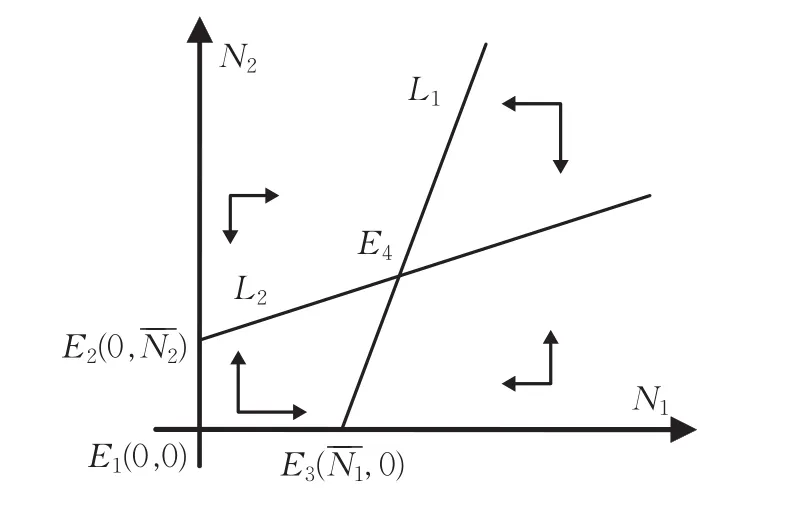
图3 共生型演化
(3)偏利偏害型演化
当模型(12)中交互关联系数 a12⋅a21<0 时,即a12>0 且 a21<0 或 a12<0 且 a21>0 ,N1和 N2呈现偏利偏害关系。此处假设N1为偏利方,N2为偏害方,即偏利系数 a12>0 且偏害系数 a21<0 。同样的,模型(12)有4个定态解同时平衡线L1和L2的轨线走向如图4所示。

图4 偏利偏害型协同演化
若,即保证系统的偏害效应系数绝对值小于N1和N2最大收益比,此时E4满足 p>0且q>0,为系统稳定解(如图4)。对于偏利偏害型系统来说,若系统能够永续生存,现实情况是偏利和偏害双方都不可能无限增长,偏利偏害系数aij随着系统增长逐渐趋向于常数,相应的项目组合交互风险的扩散轨迹表现为围绕平衡点的一组闭轨线(如图4)。因为N1,N2>0,讨论仅限于第一象限,平衡线L1和L2把区域划分为I、II、III和IV四个部分。对于平衡线L1来说,除直线上的点满足方程L1=0外,其他在直线左方L1>0,即dN1(t)/dt>0,而直线右方L1<0。类似的,在平衡线L2右方dN2(t)/dt>0,左方dN2(t)/dt>0。综合四个区域的符号和变化趋势,N1和N2呈现为逆时针方向围绕平衡点转动的曲线,揭示了系统内N1和N2此起彼伏的演进规律。
(4)混合型协同演化
对于混合型的项目组合交互风险系统来说,其扩散过程的一般模型可表征为:
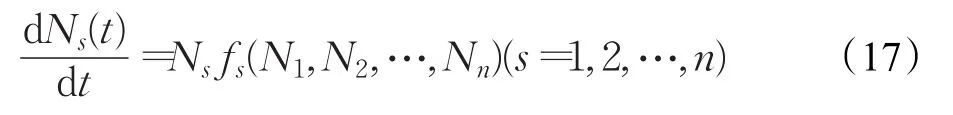
当 fi为线性函数时,混合型系统的Lotka-Volterra模型为:
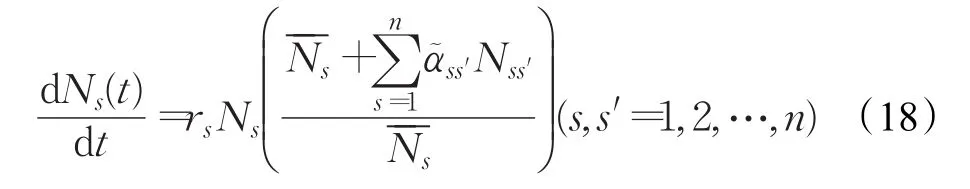
式中,若存在 s,s′=1,2,…,n 使得 ass′均不为0,则系统为环型系统,否则为链型系统,记 A=(ass′)为系数矩阵。由于项目组合风险系统内复杂交互作用,系统呈现出高维且非线性特征,而n维微分方程组在Ns≥0范围内至少有n个定态解。相比于系统解的存在性,更关心的是系统正平衡点的存在性及其全局稳定性,即当t→∞时,项目组合系统是否趋近于某正平衡位置N∗,整个项目组合是否实现长期共存。根据Liapunov函数可以推证出,若系统存在正平衡点其永续存在,其系数矩阵A须满足det(A)>0,详细论证可见文献[32]。
4.3 经济意义与解释
项目组合风险是由多主体、多要素及其因果联系形成的一类典型复杂系统,其演化动力来源于系统内部各组成单元及其结构耦合关系。组合内多个项目集中在一起,通过资源、技术和市场等风险要素间的竞争和合作,激发系统中项目的创新动力,实现项目间的优势互补,提高资源利用效率,从而达到风险配置优化和项目组合风险效益溢出。在项目组合出现之前,单项目风险与其自身的风险属性息息相关,如资源可获得性、技术支持度和市场占有率等。项目运营主体(如企业)追求的是项目最大风险效率,并保持项目的稳定增长。当一个或多个其他项目被引入后,在同一运营主体下存在多个项目,项目组合风险就表现为单项目风险到组合风险的传递和集结的过程。
当引入竞争型项目时,项目组合风险系统的演化方向和结果取决于系统内竞争效应强度和各子系统的最大收益水平。根据4.2节的模型讨论可知,具有弱竞争效应的项目组合(图2),由于竞争被约束在一定范围内,系统演化趋于稳定共存。同时根据竞争模型的均衡条件易证,当E2或E3为系统全局稳定解时,项目组合均衡条件下的收益为而对于稳定解E4来说,假设有项目组合均衡条件下的收益为即当竞争双方稳定共存时,项目组合均衡条件下的收益大于单项目的最大收益。因此,从更一般的情况出发,避免系统内的过分竞争,将竞争效应控制在一定范围内才能实现均衡条件下的项目组合风险效率的正向溢出。
当引入共生型项目时,共生效应使得项目组合交互风险系统存在正的全局稳定点,均衡条件下的子系统收益分别为益水平。同样的,项目组合均衡条件下的收益D>,且均大于其最优收因此,共生型项目组合意味着系统内项目间资源共享、技术溢出或是市场互补等产生了协同效应,从而更利于项目组合的优化配置。如在医药、软件开发等研发类企业中,知识和技术作为项目投入的核心往往消耗大量的资金和人力,为了应对未来市场的不确定性,企业常常会以最大化知识和技术的共享为竞争策略,并行开展多个项目,一方面降低资源的重复投入,充分利用已有的资源储备,另一方面也有利于提高研发类项目成功的可能性。
当引入偏利偏害项目时,项目组合风险系统的演化方向和结果取决于系统内偏害系数和偏利偏害双方的最大收益比。根据4.2节的模型讨论可知,具有弱偏害效应系统才存在稳定的正平衡点,且在稳定点上偏害方收益小于其最优收益水平,也就是说建立在偏利偏害效应的项目组合能够稳定共存的关键在于避免系统内偏害方利益的过度挤压。如实际中具有供应链关系的项目组合中,上游项目的成果或产品以低于或等于市场价格的方式供给给下游项目,以保证下游项目的正常运营,而自身丧失了正常的获利机会,如若下游项目不能实现高于正常水平的市场回报以弥补上游项目的损失,整个项目组合将呈现负溢出效应,此种情况下,上游项目应该退出,从外部寻找下游企业的供给。
对于混合型项目组合来说,其风险演化的复杂性要远远大于同类型项目组合。首先,混合型系统内风险交互关系的高维非线性使得项目组合风险系统结构出现环型或者链型传递,且这种传递很可能表现为螺旋式上升的结果。其次,混合型项目组合风险系统演化结果的正平衡点存在性更加不确定,满足系统全局稳定的条件更加严格。因此,从一般意义上说,混合型项目组合的风险控制和规避难度要远大于同类项目组合或单项目,除了要兼顾竞争型、共生型和偏利偏害型系统的风险演化特征外,更要注重其更为突出的风险放大机制。
5 结论
本研究将项目间交互关系与项目组合风险联系起来,研究项目组合交互风险系统复杂性及其协同演化问题。从探讨项目组合交互关系及其分类体系入手,将项目组合表征为具有交互耦合网络结构特征的复杂系统,提出了基于直觉模糊生态聚类算法的项目组合交互风险网络聚类的定量化方法。以此为基础,运用扩展的Lotka-Volterra模型分析了具有竞争、共生和偏利偏害效应的项目组合交互风险系统协同演化规律,并给以经济学意义上解释和扩展。本研究侧重于从一般意义上开展项目组合风险与单个项目风险之间的关系研究,其对于项目组合风险的产生和测度研究都有重要意义。
研究结果表明,项目组合风险系统复杂性取决于系统的组成单元及其结构耦合关系,组合风险产生是诸多风险信息的复杂集结过程,而项目组合交互关系是影响组合风险优化配置的关键。其中,共生型项目组合所产生的交互风险效应是同正的,决定了组合风险效率的正向溢出,而竞争型和偏利偏害型所产生的交互风险效应是可正可负的,竞争和偏害强度决定了项目组合风险的演化方向。因此,项目组合风险决策优化的有效方式即合理控制项目的配置比例,同时充分利用共生效应,避免系统内的过分竞争和偏害。
[1]Roussel P,Saad K,Erickson T.Third generation R&D:Managing the link to corporate strategy[M].Cambridge,MA:Harvard Business School Press,1991:1-7.
[2]Marle F,Vidal L A,Bocquet J C.Interactions-based risk clustering methodologies and algorithms for complex project management[J].International Journal of Production Economics,2013,142(2):225-234.
[3]Petit Y.Project portfolios in dynamic environments:Organizing for uncertainty[J].International Journal of Project Management,2012,30(5):539-553.
[4]Artzner P,Delbaen F,Eber J M,et al.Coherent measures of risk[J].Mathematical Finance,1998(9):203-228.
[5]张平,周春阳,吴冲锋.组合风险与单个资产风险间的定量关系—基于一致性风险测度的视角[J].系统管理学报,2008,17(1):15-21.
[6]Teller J,Kock A.An empirical investigation on how portfolio risk management influences project portfolio success[J].International Journal of Project Management,2013,31(6):817-829.
[7]Fang Y,Chen L H,Fukushima M.A mixed R&D projects and securities portfolio selection model[J].European Journal of Operational Research,2008,185(2):700-715.
[8]Liesio J,Mild P,Salo A.Robust portfolio modeling with incomplete cost information and project interdependencies[J].European Journal of Operational Research,2008,190(3):679-695.
[9]郭鹏,潘女兆,赵静.高新技术项目组合的双模式风险预警机制研究[J].管理学报,2011,8(10):1524-1529.
[10]Schmidt R I.A model for R&D project selection with combined benefit,outcome and resource interactions[J].IEEE Transactions on Engineering Management,1993,40(4):403-410.
[11]Baker N,Freeland J.Recent advances in R&D benefit measurement and project selection methods[J].Management Science,1975,21(10):1164-1175.
[12]Goldstein P M S,Howard M.A note on economic models for R&D project selection in the presence of project interactions[J].Management Science,1986,32(10):1356-1360.
[13]Rungi M.Success rate and resource consumption from project interdependencies[J].Industrial Management&Data Systems,2010,110(1):93-110.
[14]Solak S,Clarke J P B,Johnson E L,et al.Optimization of R&D project portfolios under endogenous uncertainty[J].European Journal of Operational Research,2010,207(1):420-433.
[15]Amir H G,Madjid T,Mohammad H K.A methodology forselecting portfoliosofprojectswith interactions and under uncertainty[J].International Journal of Project Management,2012,30(7):791-803.
[16]Martinsuo M.Project portfolio management in practice and in context[J].International Journal of Project Management,2013,31(6):794-803.
[17]Rupak B,Pankaj K,Samarjit K.Fuzzy R&D portfolio selection ofinterdependentprojects[J].Computersand Mathematics with Applications,2011,62(10):3857-3870.
[18]夏志杰,胡克瑾.基于组合方法的信息技术项目决策研究[J].计算机集成制造系统,2008,14(1):102-105.
[19]Harel E,Boaz G,Avraham S.Constructing and evaluating balanced portfolios of R&D projects with interactions:A DEA based methodology[J].European Journal of Operational Research,2006,172(3):1018-1039.
[20]Rungi M.Interdependency management:Survey comparison between small,medium and large companies[C]//Proceedings of the 9th European Academy of Management Annual Conference,Liverpool,UK,2009.
[21]郭鹏,梁俊俊,杜涛.R&D项目组合:概念、产生范式及分类[J].科学学与科学技术管理,2008,29(6):40-43.
[22]赵静,郭鹏,潘女兆.基于交互效应的项目组合风险度量及选择优化[J].运筹与管理,2011,20(6):120-126.
[23]林福永,孙凯.复杂网络关系流与行为关系定理—一般系统结构理论在复杂网络中的应用[J].系统工程理论与实践,2007(9):136-141.
[24]Lin F Y,Cheng T C.The principles and laws of general systems and their applications[J].Kybernetes,1999,28(1):75-85.
[25]张永安,李晨光.复杂适应系统应用领域研究展望[J].管理评论,2010,22(5):122-128.
[26]陈水利,李敬功,王向公.模糊集理论及其应用[M].北京:科学出版社,2005:2-10.
[27]张洪美,徐泽水,陈琦.直觉模糊集的聚类方法研究[J].控制与决策,2007,22(8):882-888.
[28]Xu Z S,Yager R R.Some geometric aggregation operations based on intuitionistic fuzzy sets[J].International Journal of General Systems,2006,35(4):417-433.
[29]Jayanthi S,Roth A V,Kristal M M,et al.Strategic resource dynamicsofmanufacturingfirms[J].ManagementScience,2009,55(6):1060-1076.
[30]满青珊,张金隆,聂磊,等.冲突影响下的移动商务联盟自组织动力建模[J].管理科学,2011,24(3):34-42.
[31]Jonghwa K,Jaekyoung A,DeokJoo L.A dynamic competition analysis on the Korean mobile phone market using competitive diffusion model[J].Computers&Industrial Engineering,2006,51(1):174-182.
[32]陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009.

