带比例因子的卷积神经网络压缩方法

徐 喆，宋泽奇

北京工业大学 信息学部，北京 100124

1 引言

目标识别一直是计算机图像处理领域中的一个热点问题，随着智能设备越来越普及，人们对识别准确率更高，实时性更好的识别算法更加迫切。在众多视觉检测方法中，基于神经网络的物体检测算法在最近几年发展迅猛。因为这种检测方法不再需要人为选取某些特定的视觉特征作为图像分类的依据，而是在训练阶段根据训练样本自适应出更加有效的特征来进行分类。神经网络虽然在检测准确率上远超传统检测方法，但是由于其内部存在大量的神经元参数，使得神经网络在检测过程中需要进行大量的计算，以至于其检测实时性相比其他算法有较大差距。

为了在准确率下降尽量小的情况下得到结构更简单，运算量更少，检测时间更短的视觉检测神经网络，2006年Caruana等人[1]提出了一种通过学习复杂模型的预测结果来实现简化网络结构的网络压缩方法，该方法通过让简单模型向复杂模型学习的手段来提高简单模型的识别能力。而后Caruana等人[2]也用实验证明通过模型压缩手段可以使结构简单的神经网络达到较高的检测准确率。2014年Li等人[3]将这种模型压缩方法成功地用在了语音识别技术中。2015年Hinton等人[4]改进了原有算法的误差计算方法，并引入了转移控制参数Q来改善softmax回归结果，使得这种模型压缩方法得到了更高的准确率，他称这种模型压缩方法为“知识提取”算法。

Geoffrey Hinton在论文中解释了这种训练方法的有效性来自于简单模型通过训练学习到了复杂模型对样本集中数据间的相近关系的理解，他以MNIST[5]手写体识别任务为例说明，如某一网络对一个样本“2”被误判为“3”的平均概率约为10－6而被误判为“7”的平均概率约为10－9。其实从这三个样本的外形中也能很明显的发现：“2”和“3”比“2”和“7”在形态上要更相近。虽然Geoffrey Hinton阐述了这一问题，但是在其方法中依然只是利用输出结果对齐的方式来达到网络压缩的目的，并没有考虑将这种相近关系量化，作为简单网络的学习内容来进一步充实压缩手段，提升压缩效果。本文以比例因子的形式量化了网络对训练样本间相近关系的理解，将其作为“知识提取”算法中简单模型通过训练学习的目标之一，充实了网络压缩手段。文章第2章详细阐述了带比例因子Z的“知识提取”训练方法，第3章通过在公开数据集中的实验结果说明了算法的有效性，并在第4章得出了实验结论。

2 带比例因子的“知识提取”方法

在传统的卷积神经网络监督训练中，前向传导过程为被训图像经过卷积层的滑窗卷积和夹杂其中的池化层来降低数据维度最终完成图像特征的提取工作，提取到的特征数据经过若干全连接层后再经过softmax回归运算[6]最终在各类别的输出端输出当前样本可能为该类别的概率值[7]。而反向传导过程则是根据最终的分类结果与训练数据集的样本标签计算误差后作为调整依据修改网络参数[8]。

2.1 基于“知识提取”的网络压缩算法

“知识提取”方法的训练原理是将一个网络结构相对简单的卷积神经网络与一个已经对同样类型的样本分类问题已经具有良好表现力的复杂卷积神经网络同时训练，使简单网络的学习目标除了标准数据集的标签外还包括复杂网络的判决结果，以使得简单网络的分类能力趋近于准确度更高的复杂网络[1]。在本文中称作为被学习对象的复杂卷积神经网络为大模型，与之对应的是网络结构较为简单的作为压缩结果的小模型。大模型在训练过程中只是与小模型对同样的训练样本进行类别预测，而不需要进行反向传导计算。对于需要进行反向传导计算的小模型，其反向计算过程中的参数调整依据除包含该网络对样本预测结果与样本标签间的误差外，还包含该预测结果与大模型对同样样本的预测结果间的误差，这两种误差通过加权和的形式来构成小模型的代价函数。

本文中大小模型对同一样本的判别误差来自于大小模型各自的softmax输出端的误差，传统的softmax回归运算的假设函数如下所示：

其中x(i)为softmax层的某一个输入样本，y(i)为与之对应的网络判别输出，θ为模型参数，k为训练样本的类别总数，j为softmax层的输出端编号，且 j∈(0,k-1)。对同一样本而言，公式中的分母为某一固定常数，则可知softmax层的k个输出端的输出值的和总为1，其中输出端数值最大者为网络对此时预测样本判别置信度最高的类别。

如果直接将传统的softmax输出结果运用到知识提取中，会出现这样的现象：除数值最大的结果输出端口外，其余端口的输出结果往往趋近于0[4]。这样的结果对于体现网络输出的类间关系很不利，因此Hinton引入转移控制参数Q[4]解决这一问题，其具体实现方式如下所示：

将大小模型的softmax层计算方法同时进行这样的修改，其中Q为“知识”转移中的转移控制参数，通常情况下将其设置为1，而在训练时将其赋值为一个大于1的整数，并保证大小模型的控制参数相等，这样可以放大softmax输出端的值，使其计算结果不再趋近于0，从而提升“知识”转移的效果，使得小模型的分类准确度能够更大程度的趋于大模型。

2.2 将比例因子加入“知识提取”算法

Hinton的“知识提取”网络压缩方法只是单纯地让大小模型的输出结果对齐，以达到使小模型的分类能力趋近于大模型的效果。但在实际应用中发现，这种趋近程度还可以通过充实小模型向大模型学习的手段进一步提升。本文通过将样本的类间相近关系加入压缩学习内容中，以期待对压缩网络的分类准确率进一步提升。

所谓类间相近关系也就是网络输出端中各端点的数值关系。为了具体量化这种各输出端之间的数值关系，这里定义“知识提取”比例因子Z，来表达大模型对于样本相似性的理解细节。比例因子Z的具体表述如下：

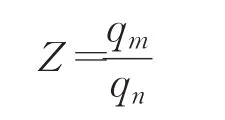
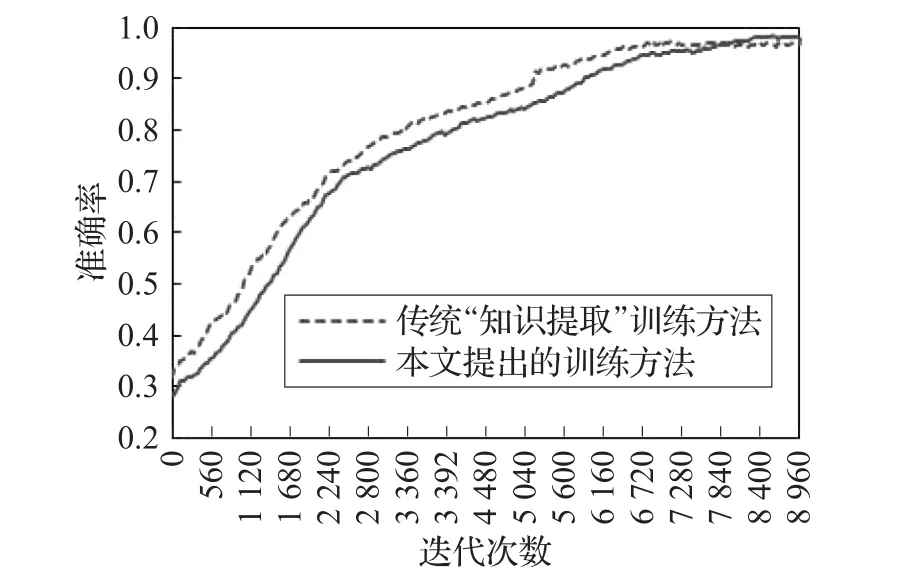
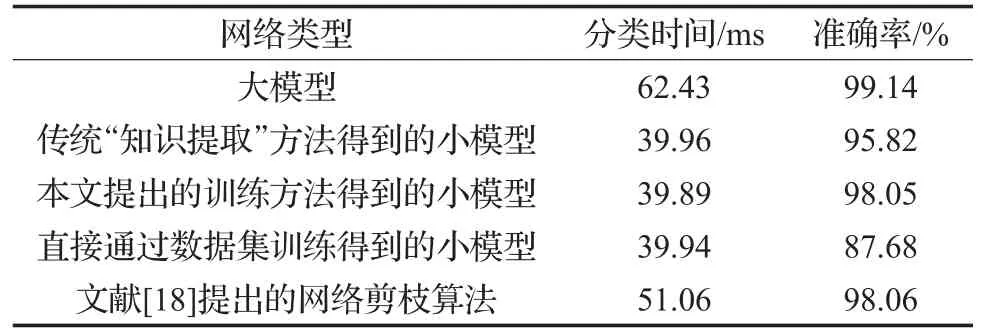
其中qn、qm表示大小模型中softmax层第n、m输出端对某一样本的带转移温度T的输出概率值，以三分类的卷积神经网络为例n、m∈(0,1,2),m

比例因子的这种网络输出端口间的输出值比较，将类间的相近关系以比例的形式进行量化，能很好地表示相近关系这一特征，且道理上简单易懂、计算过程简便高效，不会大幅提升网络训练时间。而比例因子对齐的这种做法本身就是对网络学习手段的一种扩充，这种对学习手段的扩充可以对网络学习效果起到积极的作用。

在神经网络的监督训练过程中，网络对输入样本通过前向运算输出判别结果，该结果与样本标签比较后产生判别误差。为了能够实现更准确的分类效果，网络通过判别误差对神经元参数进行调整，以使得下一轮前向计算能够输出更加精确的判别结果。而这里的判别误差就是通常所说的网络反向计算中代价函数的重要组成部分。求两模型对同一样本的比例因子间的欧氏距离W，并将其归一化后的值作为代价函数的一部分用于小模型的反向计算过程。

欧氏距离作为一种简单常见的衡量数据差别的方法，被广泛用于神经网络误差分析中，而将两网络比例因子的欧氏距离加入代价函数正是利用了神经网络的自身调节能力来使得比例因子误差量对小模型网络参数调节起到一定作用，进而使得其比例因子逐步向大模型靠近，以进一步提升小模型的网络分类准确率。如图1所示，大小模型在联合训练的过程中通过比较大小模型的输出值及其比例因子误差值产生大小模型对应输出端的误差以及大小模型比例因子的误差，而小模型与标准数据集的标签值比较得到标准数据集判别误差。最终将这三部分误差加入小模型代价函数，来对其内部参数进行调节。而神经网络的优化目的就是通过误差调节网络参数来最小化代价函数值，进而得到更高的分类准确率的目的[9-10]。

图1 带比例因子的“知识提取”算法网络结构图

3 实验

本实验分别用传统“知识提取”方法和本文提出的加入比例因子的“知识提取”网络压缩方法，对同一复杂卷积神经网络进行压缩训练，并使得压缩得到的两个简单网络在网络规模上保持一致。而后在相同的验证集上对两网络的分类准确率和分类耗时进行比较，从而达到比较传统“知识提取”压缩方法与本文提出的带比例因子的“知识提取”网络压缩方法压缩能力的目的。

本文首先采用NICTA数据集[11]进行网络压缩训练。该数据集包含3个目标类别，分别是行人、汽车和除此以外的背景。该数据集包含训练集237 344张，验证集75 148张。图2是数据集中的部分样本。

图2 NICTA数据集中的部分样本

本实验中大小模型的网络结构设计参考了经典的LeNet[5，12]手写体分类神经网络模型。大模型包含3个卷积层，各卷积层后分别跟随着1个池化层来降低特征复杂程度，在卷积结束后又通过4个全连接层以及1个softmax回归层来进行分类和各类别的概率输出。小模型则包含2个卷积层，3个全连接层以及1个softmax回归层，小模型省略的包含150个通道和包含800个通道的全连接层会使其网络参数数量大大降低，从而获得更高的分类速度。网络压缩训练的实验参数如表1所示，具体的大小模型网络结构如表2、3所示。

表1 压缩训练实验参数说明

在网络训练中采用了AdaDelta[13]、Dropout[14]方法来尽量地抑制网络过拟合问题，使得网络能够得到更好的泛化能力，其中Dropout算法已经在著名的AlexNet[15]网络中证明了其出色的抵抗过拟合能力。

神经网络训练中的参数调整依据是网络对训练集当前的判决误差，为了避免网络参数过度拟合于训练集而偏离了真实情况，需要在训练过程中通过网络对验证集的分类情况对网络的决策能力进行较客观地评价。图3、4是某次训练过程中神经网络对验证集分类准确率和训练集分类代价函数值的分布记录情况，其中传统“知识提取”方法采用了Geoffrey Hinton的知识提取算法[4]，而直接通过数据集训练的神经网络模型与小模型有着相同的网络结构。从图4中传统“知识提取”方法的代价函数值变化情况，可以发现这个值通常要小于加入比例因子的网络代价值，而加入比例因子方法的代价函数之所以较大，就是因为将比例因子也作为网络压缩训练的目标，将其误差值也作为代价函数的一部分来进行网络参数调节。图4中也描述了本文提出的网络训练方法中由于比例因子引起的带来的代价值，如上所述这个值正是大小模型比例因子误差的归一化值，可以发现这个值随着迭代次数的增加在逐渐减小并最终趋近于零，这说明小模型通过调整网络参数基本可以和大模型的比例因子保持一致。观察图3发现本文提出的训练方法所得到的神经网络较传统“知识提取”方法而言其分类准确率变化缓慢，且前期准确率较低，但其准确率的最终稳定值却高于传统“知识提取”训练方法。这说明在代价函数中添加比例因子误差量会使得网络参数调整所参考的目标更加丰富，进而使得加入比例因子的训练方法得到的小模型的分类准确率更接近于网络结构复杂，分类耗时较长，但准确率更高的大模型。

图3 不同方法在验证集上的准确率分布

图4 不同训练方法的代价函数值分布情况

表2 大模型的网络结构说明

表3 小模型的网络结构说明

表4为不同网络在NICTA验证集上的分类时间和准确率平均值，测试硬件平台为CPU：I7-6700，GPU：GTX-TITAN X。从表中可以发现“知识提取”训练方法可以很好地让小模型的分类准确率趋近于大模型，从而平衡网络的分类耗时和准确率问题。而本文提出的增加比例因子的“知识提取”训练方法在分类时间保持不变的情况下又使得这种趋近程度进一步提高，使得相同网络结构的小模型能够得到更高的分类准确率。

表4 不同模型在NICTA验证集上的检测结果对比

为了更加客观地对本文的算法进行验证，在ETHZ数据集[16]和TUD数据集[17]上对压缩方法进行验证。考虑到目前网络加速可以通过多种途径实现，为了对比本文所提出算法与同类型算法的实际效果，采用文献[18]提出的网络剪枝算法对大模型进行处理而后通过数据集进行验证，文献[18]通过对网络参数的相关性进行量化来判断网络参数的变化对网络性能的影响，而后按照一定标准对网络中一些不重要的参数进行删除以达到网络加速的目的。实验结果如表5、6所示，该结果表明加入比例因子的“知识提取”网络压缩方法在这两个数据集上同样表现出较传统“知识提取”方法更好的压缩能力。而与文献[18]所提出的网络加速算法相比，本文展现出了更好的加速效果，从实验数据来看文献[18]所提出的算法虽然在准确率下降不明显的情况下通过网络剪枝起到了加速效果，但是通过对网络冗余参数进行裁剪的方法在参数下降规模上还是不及本文提出的网络压缩算法，导致其实际速度提升效果没有本文提出的算法明显。

表5 不同模型在ETHZ验证集上的检测结果对比

表6 不同模型在TUD验证集上的检测结果对比

4 结束语

本文在原有的“知识提取”网络压缩方法上，将网络对分类样本的在各输出端的这种类间关系理解量化为比例因子。并在训练中将两网络的比例因子误差作为被压缩网络代价函的一部分，来对被压缩网络的参数进行调节，扩充了网络学习手段。观察上述实验可以发现，通过本文提出的压缩方法得到的小模型其分类准确率较原本的“知识提取”算法有了一定的提升。这说明本文提出的加入比例因子的“知识提取”模型压缩方法可以更好地将大模型的分类能力转移到小模型从而达到在尽量保持网络分类能力的前提下减小模型复杂度进而达到提高实时性的效果。

如今对网络加速算法的研究日趋广泛，而网络加速的途径也越来越多，如果能将“知识提取”与这些算法进行协同训练，进而取得一加一大于二的性能，无疑会有更加强烈的实用价值，而这也将是未来研究的方向。

[1]Buciluǎ C，Caruana R，Niculescu-Mizil A.Model compression[C]//Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，2006：535-541.

[2]Ba J，Caruana R.Do deep nets really need to be deep?[C]//Advances in Neural Information Processing Systems，2014：2654-2662.

[3]Li J，Zhao R，Huang J T，et al.Learning small-size DNN with output-distribution-based criteria[C]//INTERSPEECH，2014：1910-1914.

[4]Hinton G，Vinyals O，Dean J.Distilling the knowledge in a neural network[J].arXiv preprint arXiv：1503.02531，2015.

[5]LeCun Y，Bottou L，Bengio Y，et al.Gradient-based learning applied to documentrecognition[J].Proceedingsofthe IEEE，1998，86（11）：2278-2324.

[6]Unsupervised feature learning and deep learning-softmax regression[EB/OL].http：//deeplearning.stanford.edu/wiki/index.php/Softmax_Regression 2013-04-07/2016-08-24.

[7]Zeiler M D，Fergus R.Visualizing and understanding convolutional networks[C]//European Conference on Computer Vision，2014：818-833.

[8]Goodfellow I，Bengio Y，Courville A.Deep learning[M].[S.l.]：The MIT Press，2016.

[9]LeCun Y，Bengio Y，Hinton G.Deep learning[J].Nature，2015，521（7553）：436-444.

[10]Hagan M T，Demuth H B，Beale M H，et al.Neural network design[M].Boston：PWS Publishing Company，1996.

[11]Overett G，Petersson L，Brewer N，et al.A new pedestrian dataset for supervised learning[C]//2008 IEEE Intelligent Vehicles Symposium，2008：373-378.

[12]金连文，钟卓耀，杨钊，等.深度学习在手写汉字识别中的应用综述[J].自动化学报，2016，42（8）：1125-1141.

[13]Zeiler M D.ADADELTA：An adaptive learning rate method[J].arXiv preprint arXiv：1212.5701，2012.

[14]Srivastava N，Hinton G E，Krizhevsky A，et al.Dropout：A simple way to prevent neural networks from overfitting[J].Journal of Machine Learning Research，2014，15（1）：1929-1958.

[15]Krizhevsky A，Sutskever I，Hinton G E.Imagenet classification with deep convolutional neural networks[C]//International Conference on Neural Information Processing Systems，2012：1097-1105.

[16]Ess A，Leibe B，Schindler K，et al.A mobile vision system for robust multi-person tracking[C]//IEEE Conference on Computer Vision and Pattern Recognition，2008（CVPR 2008），2008：1-8.

[17]Wojek C，Walk S，Schiele B.Multi-cue onboard pedestrian detection[C]//IEEE Conference on Computer Vision and Pattern Recognition，2009（CVPR 2009），2009：794-801.

[18]费芸洁，邓伟.一种基于灵敏度分析的神经网络剪枝方法[J].计算机工程与应用，2007，43（7）：34-35.