基于输入约束一致性算法的多无人机编队控制

熊 涛，曹科才，2，柴 运，徐培娟

1.南京邮电大学 自动化学院，南京 210023

2.南京航空航天大学 自动化学院，南京 210016

1 引言

近年来，由于多无人机系统的鲁棒性、灵活性、可扩展性及经济性等因素，多无人机系统协调控制得到了越来越多的关注[1-3]。作为多无人机协调控制最基本的一种控制方法，多无人机的一致性控制问题一直以来都是控制领域的研究热点[4-6]。一致性控制是指无人机利用自身配置的传感器来感知周围无人机的信息，从而实现无人机之间信息的交互与共享。关于多无人机系统的一致性控制问题，目前已取得了一些成果。文献[7-8]将多无人机系统简化成一阶动态系统，在基于文献[9]提出的多智能体一致性算法的基础上，提出了一种基于一致性反馈线性方法解决了没有明确领航无人机的多无人机编队控制问题。文献[5]将多无人机模型反馈线性化成了二阶动态模型，研究了带有虚拟领航无人机的多无人机系统的分布式编队控制问题。文献[10]利用经典控制理论与逆动力学理论，研究了基于虚拟结构方法的无人机的编队飞行，并通过非线性六自由度的仿真验证了方法的有效性。文献[11-12]考虑了存在时延情况下的多无人机的一致性控制及编队控制，通过对定常时延以及时变时延两种情况设计一致性控制算法研究了多无人机的编队控制。文献[13]考虑无人机编队时无明确领航者，每一个无人机都是基于邻居状态信息，研究了非均匀时延以及共连通拓扑约束下的无人机在三维空间中编队控制。文献[14]用线性矩阵不等式方法研究了切换通信拓扑下具有二阶积分特性的多无人机群的编队控制问题。注意到，现有文献中利用输入约束的一致性控制算法对多无人机系统一致性控制研究较少，且现有文献中存在将无人机模型直接化简成一阶或者二阶动态系统，忽略了很多无人机的非线性因素。另外现有文献主要考虑了多无人机系统的平面一致性控制，而缺少空间编队控制的研究。

级联系统，顾名思义，是由多个子系统通过子系统之间状态的相互关联而组成。利用级联系统理论将复杂的模型简化成若干个子系统的级联形式来研究非线性系统的控制问题是一种有效的方法。将复杂的系统模型化简成级联形式，避免了直接忽略多项非线性因素将系统模型化简成简单的低阶或者高阶系统所带来的模型不准确性。文献[15]给出了非自治级联系统的稳定性分析。文献[16]利用文献[15]中的非自治级联系统的稳定性分析方法，通过将非完整链式智能体系统化成级联形式研究了其编队跟踪控制问题。

2 系统模型及问题描述

文献[17]根据牛顿-欧拉方法得到了垂直起降无人机系统模型，系统方程表示如下：

其中，m表示无人机的质量，I表示无人机的惯性矩阵；T表示无人机的推力，产生沿机体坐标系k方向上的运动；Γ∈R3表示转矩矢量，控制无人机姿态；ξ=(ξ1,ξ2,ξ3)T∈R3表示的是无人机的质点在惯性坐标系中的位置；R∈SO(3)表示机体坐标系相对惯性坐标系的旋转矩阵；d(t)表示无人机的外部扰动；ω=(ω1,ω2,ω3)T∈R3是无人机在机体坐标系中的角速度矢量；Fe表示作用于无人机上的全部外力；ΣR为常数耦合矩阵；e3=(0,0,1)T表示机体坐标系中k方向的单位向量；S(⋅∙)是斜对称矩阵，式（1）中 S(ω)可写为：

考虑N个机械结构都相同的垂直起降无人机模型组成的系统，系统方程可以表示为：

其中，i=1,2,…,N 。

基于级联系统理论，可令 xi1=miξi，xi2=miξi，且假设作用于无人机的外部力矩减小到与无人机重量相同，即Fe=mge3。根据模型（3）可得：

其中，xi3=-TiRie3+mge3,ui1=RiΣRΓi。对 xi3求导为：

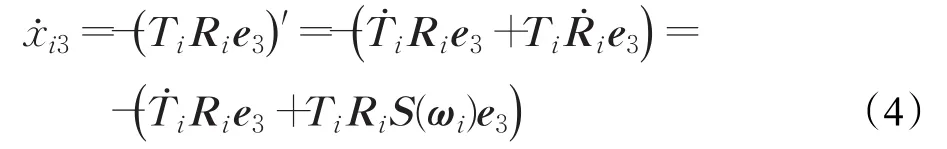
根据矩阵 S(ω)的定义（2），令 xi3=xi4，且由于T 仅表示无人机机体k方向的推力，所以式（4）可化简为：

其中，δ=(Tiωi2,-Tiωi1,Ti)T。对xi4求导可得：

将式（3）代入式（6），整理可得：

联立式（4）～（7），模型（3）可转化为以下级联形式：

其中

通过以上化简可以看出，本文基于原始的无人机系统模型，将其化简成级联形式，避免了忽略无人机所收到的外力而造成不能对模型准确描述。相对的，文献[7]考虑了无人机在二维平面的编队控制问题，其中，作者将无人机系统简化成以下一阶模型：

其中，ri∈R2表示第i个无人机的位置，ui∈R2表示第i个无人机的控制输入。系统式（9）从广义上说可以代表任意的多智能体系统，并不能特指多无人机系统。无人机系统是一个多输入多输出且具有多自由度的非线性系统，考虑理想情况下并忽略一些外力因素，将模型线性化可以达到理论研究效果，但此类方法应用到实际无人机系统中往往不能够达到精确的控制目的。本文的主要贡献在于基于原始的垂直起降无人机模型，利用级联系统理论将复杂的无人机模型化简成级联形式，而不是直接将无人机模型化简成简单的一阶动态模型。在控制器设计时利用双曲正切函数的有界性质研究了基于输入约束下的一致性算法的多无人机编队控制问题。为了更能够说明本文所提控制方法的有效性，本文还对无人机在三维情况下的编队情况进行了仿真研究。

多无人机系统一致性控制问题描述如下：对于多无人机系统模型（3），通过感知周围邻居无人机的信息，使得系统中的所有无人机在所设计的控制器作用下最终能够达到一致状态。即对于级联后的系统模型（8），构造一致性算法，使得：

其中，i=1,2,…,N 。

3 控制律设计

在前人工作的基础上，针对多无人机系统一致性控制问题，利用双曲正切函数的有界性质，通过在控制器设计时引入双曲正切函数使得系统（8）中的所有状态达到全局一致性。首先设计控制律ui1如下：

其中，k1>0，k2>0是正常数，Ni表示与第i个无人机能够通信的邻居无人机的集合。

tanh(x)=(ex-e-x)/(ex+e-x)是有界函数，并且有tanh(x)=sinh(x)/cosh(x),sinh(x)=(ex-e-x)/2，cosh(x)=(ex+e-x)/2。因为tanh(x)是有界的，故ui1也是有界的。假设由N个智能体组成的系统其通信拓扑结构可以由图G=( )

V,E 来表示，图G表示由若干个节点以及组成这些节点的边组成的图形，V表示顶点的集合，其包括图中所有的节点，E表示边的集合，其包括所有组成节点的边。aij是邻接矩阵A=[eij]∈ℝn×n中的元素，其可当(j ,i)∈E时，aij=1；当(j ,i)∉E时，aij=0。aij=1表示第i个无人机可以接受第 j个无人机的状态信息。aij=0则表示第i个无人机不能接受第 j个无人机的状态信息。图G的度矩阵为 D=[dij]∈ℝn×n，当i=j时，L=[lij]∈ ℝn×n表示图G的Laplacian矩阵，当i=j时，当i≠j时，lij=-aij。

对控制输入ui2设计如下形式：

其中，k3>0，k4>0为正常数。

4 主要结果

为了后续理论证明，首先定义矩阵 Z1=[x11,x21,…,xN1]T,Z2=[x12,x22,…,xN2]T,Z3=[x13,x23,…,xN3]T,Z4=[x14,x24,…,xN4]T。在给出本文主要结果之前，首先给出以下引理。

引理1[14]考虑一个时变级联系统z=f( )t,z，可以将其写成：

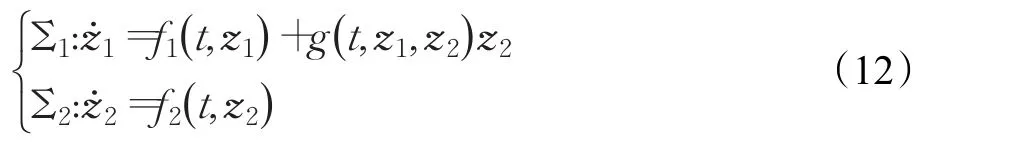
其中，z1∈ℝn,z2∈ℝm。函数 f1(t ,z1)在(t ,z1)处是连续可微的，f2(t ,z2)和g(t ,z1,z2)是局部Lipschitz的。系统式（12）可以看成是系统：

受到系统Σ2的输出扰动。

引理2[14]如果满足以下条件，那么，级联时变系统（12）将达到全局一致稳定：

（1）子系统（13）是全局一致稳定的；

（2）级联函数g(t ,z1,z2)对所有t≥t0满足以下条件：

其中，θ1:ℝ+→ℝ+,θ2:ℝ+→ℝ+是连续函数；

（3）子系统Σ2是全局一致渐近稳定的。

根据以上引理，给出本文主要结果，如下：

定理1假设系统通信拓扑结构为固定无向连通图，如果k1>0和k2>0是常数，且 L∈ℝn×n是系统无向连通图的Laplacian矩阵，那么系统

将达到全局一致稳定。

证明 选择Lyapunov函数为：

因为cosh(x )≥1，ln[c osh(xi-xj) ]≥0，aij≥0，故式（15）为正定的，对其求导得：

根据式（8）、式（17）进一步化简可得：

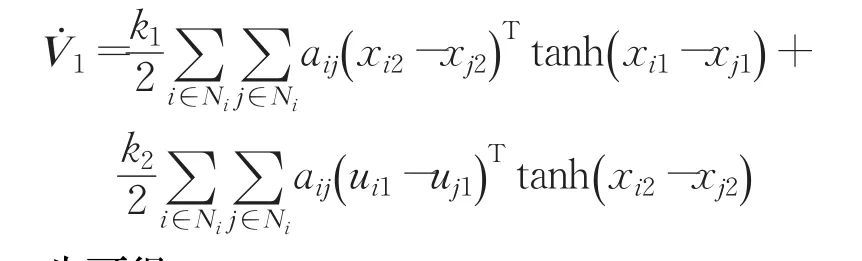
进一步可得：

且对于无向连通图有aij=aji，则以上可写成：

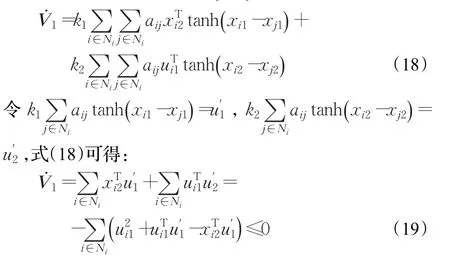
因此，根据Lyapunov稳定性理论可知，系统式（15）是全局一致稳定的。

定理2假设系统通信拓扑结构是固定无向连通图，则系统式（8）在控制律式（10）和式（11）作用下能够达到全局一致稳定。

证明 在控制律式（10）和式（11）的作用下，系统式（8）可以写成如下形式：

根据级联系统原理，系统式（19）可以被看成是系统式（15）被以下系统：

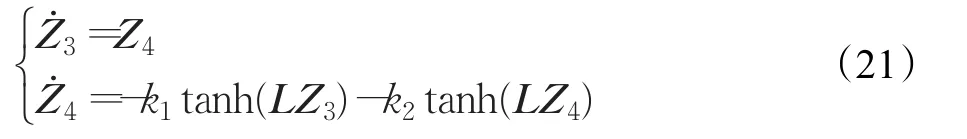
级联，级联项为Z3。

（1）根据定理1，如果系统的通信拓扑结构是固定无向连通的，则子系统式（15）是全局一致稳定的；当V1=0时，从式（19）可得，Z2=0，则从公式（15）易得 Z1=0，根据不变集理论，子系统式（21）根据定理1可证明是全局一致渐近稳定的。

（2）级联项 Z3满足式（14）条件。

基于以上两个条件，再根据引理2可知，系统拓扑结构为固定无向连通情况下，系统式（8）在控制律式（10）和式（11）的作用下能够达到全局一致稳定，证毕。

定理3假设系统通信拓扑结构是固定无向连通图，则系统式（8）在以下编队控制算法作用下能够收敛到给定值，即形成固定的队形。

其中，都为正常数分别表示各状态之间的编队距离。定理3的证明过程与定理1、定理2类似，此处不再重述。

5 仿真验证

本章基于Matlab仿真平台直接对级联后的模型式（8）进行数值仿真研究，进一步阐述所提控制方法的有效性。基于所提一致性算法的控制思想对多无人机系统一致性控制及编队控制进行仿真研究。为了验证所提控制方法的有效性，本文对比了无人机输入不受约束情况下无人机的运动情况。

5.1 一致性仿真

假设系统是由6架具有相同机械结构的无人机组成的多无人机系统，每一个无人机只能够和其邻居无人机相互通信，系统通信拓扑结构如图1所示。

根据图论相关知识，多无人机通信拓扑结构图的信息可由以下矩阵表示，其中矩阵为D度矩阵，矩阵L是Laplacian矩阵，其定义见第3章：

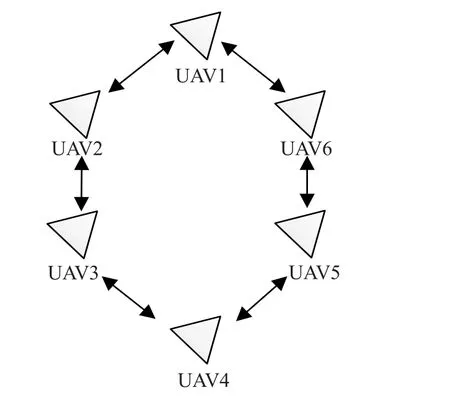
图1 6架无人机的通信拓扑结构

对输入约束下多无人机一致性控制问题研究时对比研究了输入不受约束情况下无人机系统各状态的变化情况。假设两组实验仿真数据一致，各状态初始值为下：6架无人机状态 xi1初始值为{-30,-10,0,2,10,50}；6架无人机状态xi2初始值为{10,0.1,2.5,0,-5.5,-10}；6架无人机状态 xi3初始值为{0.15,0.3,-0.2,0.5,-0.1,0.4}；6架无人机状态 xi4初始值为{0.5,0.1,0.12,0.4,0.12,0.18}。

图2～图5为输入不受约束下无人机级联系统各状态的变化情况，图6～图9表示了输入约束下无人机级联系统各状态的变化情况。

当无人机控制输入不受约束时，状态xi3和状态xi4能够达到一致，但是由于控制输入过大，系统会发生饱和作用，所以状态xi1和状态xi2无法达到一致。

图2 输入不受约束下xi1的一致性

图3 输入不受约束下xi2的一致性

图4 输入不受约束下xi3的一致性

图5 输入不受约束下xi4的一致性

图6 输入约束下xi1的一致性

图7 输入约束下xi2的一致性

图8 输入约束下xi3的一致性

图9 输入约束下xi4的一致性

从图6～图9可以看出，在所设计输入约束一致性算法作用下，无人机级联系统4个状态都能够趋于一致。为了更好地说明方法的有效性，通过对每个状态建立3组元素作为无人机在空间中3个坐标轴的数据，选择6架无人机初始位置为[30,-30,-30]、[90,-10,70]、[40,0,30]、[0,2,-40]、[10,10,-20]、[-50,50,-100]，无人机在空间中运动轨迹如图10所示，从图10可以看出，无人机在空间中最终能够趋于一致的状态。

图10 无人机在空间中的一致性

5.2 编队仿真

编队控制可以看成是一致性控制的延伸，本节将基于编队控制算法式（21）和式（22）对系统模型式（8）进行编队控制仿真研究。考虑3个无人机的直线编队，且系统通信拓扑结构为无向连通图，如图11所示。

图11 三架无人机的通信拓扑结构

根据图论相关知识，多无人机通信拓扑结构图的信息可由以下度矩阵和Laplacian矩阵表示：

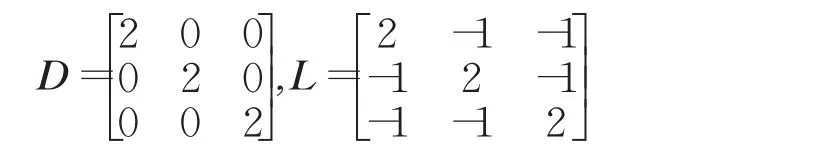
基于所设计的一致性控制算法，3架无人机在空间中初始位置为[10,1,-3]、[-6,3,7]、[7,-5,3]。无人机在空间中编队控制的运动轨迹如图12所示，从图中可以看到，系统中3架无人机在所涉及的编队控制算法下最终能够保持直线队形运动。

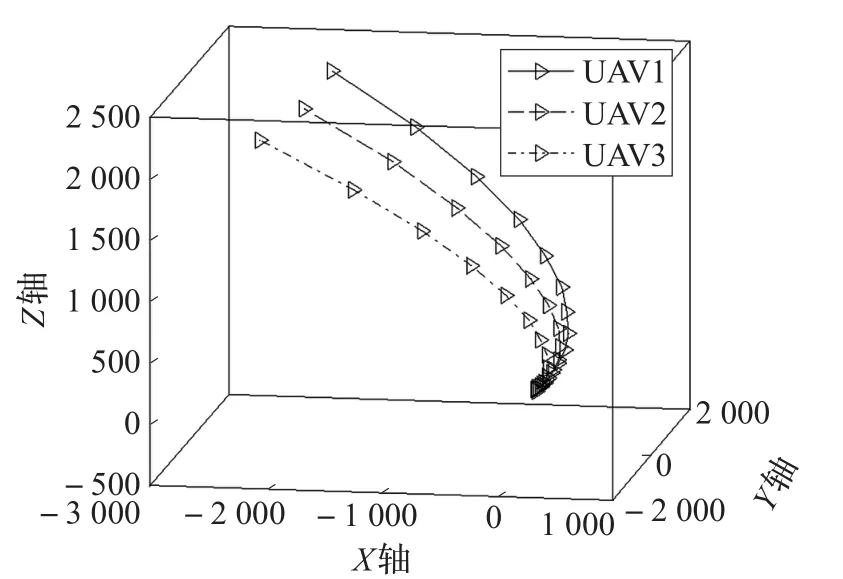
图12 无人机在空间中的编队

6 结束语

本文针对复杂的多无人机系统模型，通过利用级联系统理论处理复杂非线性模型的优点，将一般性的多无人机模型简化为级联形式，然后针对级联后的系统模型，基于输入约束一致性控制算法对多无人机编队控制问题进行了研究。利用双曲正切函数的有界性质，通过在控制器设计时引入双曲正切函数研究了在输入约束一致性算法下系统的一致性控制问题。最后，将输入约束一致性算法思想应用到编队控制算法的设计中，研究了多无人机的编队控制问题。基于Matlab仿真平台对所提出的控制算法验证其有效性，仿真结果表明，在所提出的一致性控制算法的作用下，级联后系统所有状态最终都能够得到收敛到一致。在基于输入约束一致性控制算法思想设计的编队控制算法下，多无人机能够形成固定的队形，表明了所提控制方法的有效性。本文假设系统通信拓扑结构为固定无向的通信拓扑，后续考虑具有约束情况下具有切换拓扑结构的多无人机一致性控制问题值得去研究。

[1]Wang P，Ding B.Distributed RHC for tracking and formation of nonholonomic multi-vehicle systems[J].IEEE Transactions on Automatic Control，2014，59（6）：1439-1453.

[2]Guerrero J A，Lozano R.Flight formation of multiple mini rotorcraft based on nested saturations[C]//IEEE International Conference on Intelligent Robots and Systems，2010：634-639.

[3]Liao F，Teo R，Wang J L，et al.Distributed formation and reconfiguration control of VTOL UAVs[J].IEEE Transactions on Control Systems Technology，2017，25（1）：270-277.

[4]Aldo S J B，Mo J.Consensus-based and network control of UAVs[C]//International Conference on System of Systems Engineering，2010：1-6.

[5]王品，姚佩阳.多无人机系统分布式编队控制[J].计算机工程与应用，2016，52（16）：1-6.

[6]Rinaldi F，Chiesa S，Quagliotti F.Linear quadratic control for quadrotors UAVs dynamics and formation flight[J].Journal of Intelligent&Robotic Systems，2013，70（1）：203-220.

[7]Kuriki Y，Namerikawa T.Consensus-based cooperative control for geometric configuration of UAVs flying in formation[C]//SICE Conference，2013：1237-1242.

[8]Joongbo S，Chaeik A，Youdan K.Controller design for UAV formation flight using consensus based decentralized approach[J].AIAA Journal，2009，251（6）：6-9.

[9]Olfati-Saber R，Fax J A，Murray R M.Consensus and cooperation in networked multi-agent systems[J].Proceedings of the IEEE，2007，95（1）：215-233.

[10]Askari A，Mortazavi M，Talebi H A.UAV formation control via the virtual structure approach[J].Journal of Aerospace Engineering，2015，28（1）：401-433.

[11]Wang Z，You K，Xu J.Consensus design for continuous time multi-agent systems with communication delay[J].Journal of Systems Science and Complexity，2014，27（4）：701-711.

[12]Li W，Chen Z.Leader-following consensus of secondorder time-delay multi-agent systems with and without nonlinear dynamics[J].Journal of University of Science&Technology of China，2012，42（5）：415-422.

[13]Xue R，Cai G，Xue R，et al.Formation flight control of multi-UAV system with communication constraints[J].Journal of Aerospace Technology&Management，2016，8（2）：203-210.

[14]Zhou Y，X Dong，G Lu.Time-varying formation control for unmanned aerial vehicles with switching interaction topologies[C]//InternationalConference on Unmanned Aircraft Systems，2014，46：26-36.

[15]Panteley E，Loria A.On global uniform asymptotic stability of nonlinear time-varying systems in cascade[J].Systems&Control Letters，1998，33（2）：131-138.

[16]Cao K C，Yang H，Jiang B.Formation tracking control of nonholonomic chained form systems[C]//IEEE International Conference on Control and Automation，2013：846-851.

[17]Hua M D，Hamel T，Morin P.Introduction to feedback control of underactuated VTOL vehicles[J].IEEE Control Systems Magazine，2013，33（1）：61-75.