无标度网络中考虑个体重视的传染病传播研究
王 燕,罗彦君
兰州理工大学 计算机与通信学院,兰州 730050
1 引言
近年来,随着复杂网络理论在各领域的发展,传染病的传播已经成为一个热门的研究课题并吸引了很多学术界的关注和兴趣。如SARS、禽流感和甲型H1N1等传染疾病的传播。为了描述传染病在网络中的传播动力过程,许多研究人员已经研究了多种传播模型,如SI模型[1-3]、SIS模型[4-7]、SIR 模型[8-10]、SIRS模型[11-12]。这些模型的研究在预测和控制传染病的传播中起着重要的作用。随着研究的深入,对传染病的传播问题的研究也层层递进。为了进一步了解现实世界中传染病的传播动态,许多研究人员对无标度网络上的传染病传播进行了研究。Pastor-Satorras与Vespignani研究了无标度网络中的病毒传播。研究发现,无限大规模的无标度网络中的病毒传播临界值趋于0也就意味着只要病毒传播率大于0,病毒就能传播[13]。Huang等人基于SIR传播模型在无标度网络中研究了具有相同传染性的病毒传播动力学行为。研究发现,如果模型的基本再数小于1,则无疾病平衡在全局渐近稳定,否则,地方性平衡在全球渐近稳定[14]。Kang等人在无标度网络上研究了具有时滞的传染病传播行为,发现时滞可以影响传染病达到均衡的收敛速度[15]。然而上述的研究多关注于网络上单类型的传播动力学问题,如网络拓扑对疾病爆发的阈值(或者说疾病的基本再生数)和传播范围的影响;不同传播模型在不同网络拓扑下的传播阈值和传播范围;针对不同网络,如何设计有效的免疫策略等。
但是值得注意的是,仅仅从传染病传播动力学本身出发是不够全面的。因为在现实生活中,传染病的爆发必然会引起个体的反应,而个体的反应会反过来影响传染病的传播。许多研究人员对个体行为反应与传染病之间的相互作用进行了研究。例如,Liu等人考虑局域信息的意识行为,在SIR模型的基础上引进一个新的状态——警觉状态(SF),所有处于警觉状态的健康个体的感染率都相同并且小于易感染态的概率。研究表明,局部意识行为可以降低疾病的传播阈值和感染范围[16]。Meloni等人研究个体迁移对传染病的影响即个体为了自我保护从传染病流行度高的地区迁移到相对安全的地区,研究表明这种行为会使传染病更大范围地扩散[17]。Li等人在无标度网络中引进反馈机制即健康个体会有意识地主动减少与邻居感染个体接触的次数来降低被感染的概率。研究表明,反馈机制的引入能够减缓疾病蔓延和最终被感染个体的规模[18]。
上述文献都研究了在健康个体知道传染病后所有个体针对传染病的采取的反应是一致的,并且采取行为反应的个体对传染病的重视程度都是一样情况下的传染病传播特性。但是在真实生活中每个个体的反应是不相同的,当个体知道有传染病这一消息后,有些个体认为性命攸关就非常重视,然而也有些个体认为无关紧要就不重视传染病,重视传染病的易染个体也称为具有个体重视的易染个体。具有个体重视的易染个体一般采取一些行为来预防被感染如减少出门、戴口罩、讲卫生等。并且每个具有个体重视的易染个体对传染病的重视度不一定相同。根据上述因素,本文在经典的SIR模型上提出了一种无标度网络中具有个体重视的SIR模型。引入网络的基本度量参数和具有个体重视的易染个体所占的比例p以及个体重视度α,并以此建立所提模型的动力学方程。运用平均场理论方法求解所建动力学方程,并分析所提出模型的动力学行为。研究改进的和标准的模型传播阈值和分析具有个体重视的易染个体的比例和个体重视度对传染病传播过程的影响。
2 基于个体重视的SIR模型
2.1 经典的SIR模型
在无标度网络的SIR模型中,每一个节点代表一个个体,边表示个体之间的联系。在SIR模型中,个体有三个基本的状态:易染状态(susceptible)、感染状态(infected)和被移除状态(removed)。经典的SIR模型描述一类易染个体被治愈后变成免疫状态的传染病,而且免疫状态的个体不会再次被感染变成感染状态,也不具有传染特性。其感染机制如图1所示。

图1 经典的SIR模型
其中每个时间步内,每个易感染个体如果和感染个体接触,则易感染个体以λ的概率被感染变成感染个体,感染个体则以μ的概率被治愈变成被移除个体。在每一个给定的时刻,个体处于三种状态之一,其中Sk(t)、Ik(t)和Rk(t)分别表示在t时刻度为k的三类个体所占群体的比例,并满足归一化条件:

基于平均场理论可得,无标度网络中Sk(t)、Ik(t)和Rk(t)随时间t演化的非线性微分方程为:
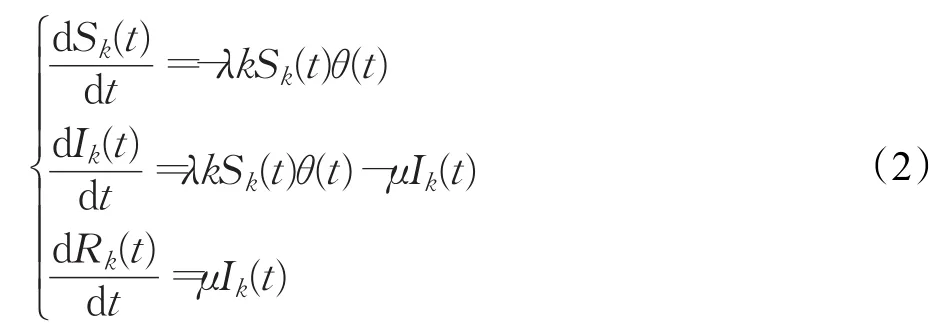
θ(t)为定义的辅助函数,表示t时刻任意一个节点与感染节点相连的概率。因此θ(t)独立于节点的度,可以表示为:

其中为网络中节点的平均度数。
2.2 改进的SIR模型
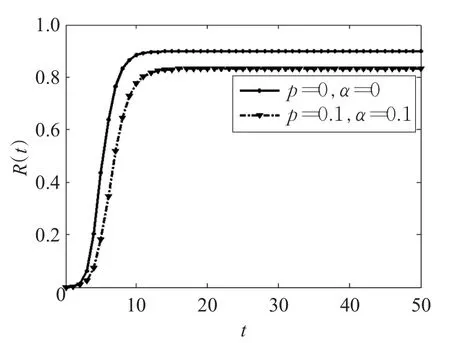
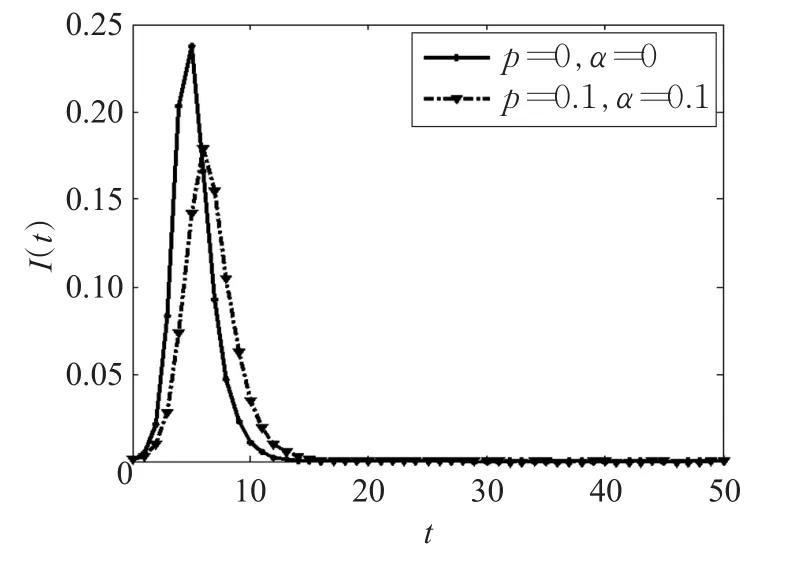
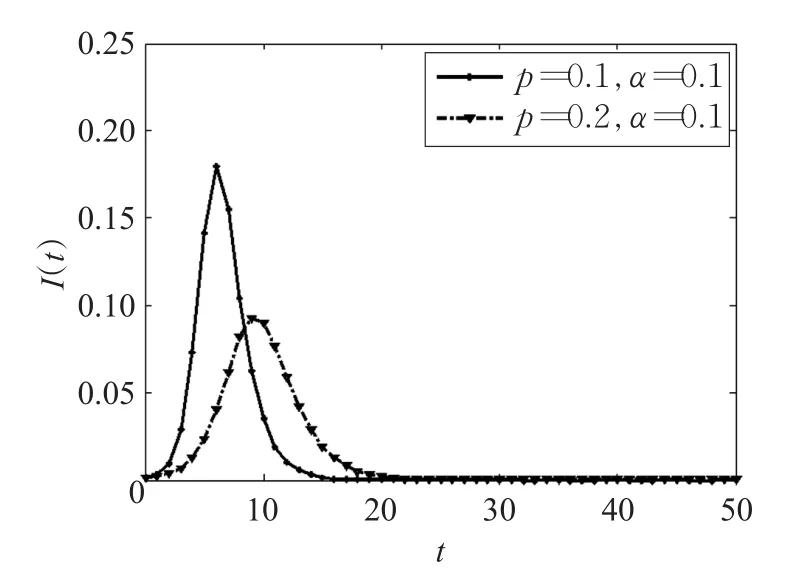
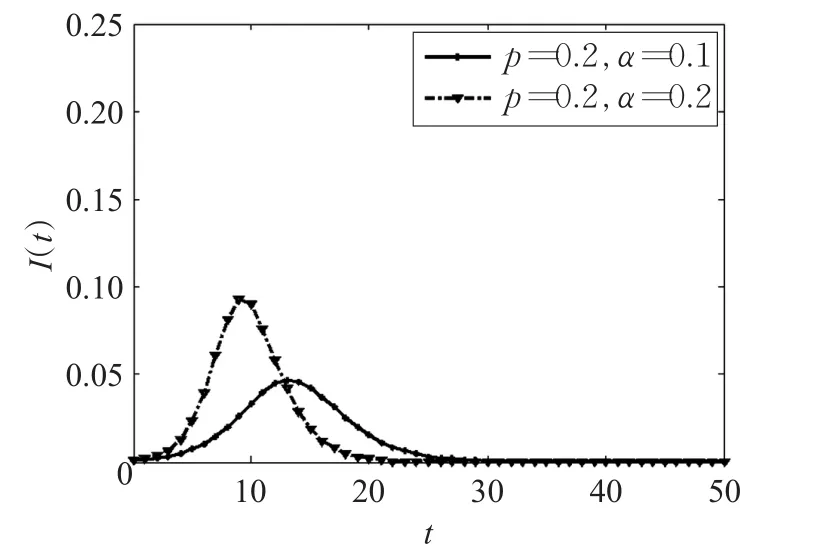
在改进的模型中,假设在个体总数N恒定下,具有个体重视的易染个体所占的比例为p(0 (1)具有个体重视的易染个体,则以λ′的概率变成感染个体。或者不具有个体重视的易染个体则以λ的概率变成感染个体。 (2)被感染个体以概率β被治愈变成被移除个体。 改进模型如图2。 图2 改进的SIR模型 由于无标度网络中的节点是不均匀的,所以每个健康个体的邻居感染数不同。因此,每个具有个体重视的不同度的易染个体的重视程度是不一样的。根据无标度的异质性,每个具有个体重视的易染个体的邻居被感染的越多,易染个体的重视度越大,易染个体被感染的概率就越低。因此用邻居感染数kinf和一般个体重视度α来刻画具重视传染病的个体的重视度。设kinf为度为k的易染个体的感染邻居数,α为具有个体重视的易染个体了解某个邻居被感染后的个体重视度,则无标度网络中度为k的易染个体的个体重视度为g(α,kinf)=1-(1-α)kinf。易染个体的重视度越大越容易采取措施来降低被感染的可能性,进而导致具有个体重视的易染个体的感染率降低,因此具有个体重视的易染个体的被感染率可以定义为:λ'=(1-g)λ=(1-α)kinfλ。 根据图2所示的SIR传播模型,由动力学平均场理论可得Sk(t)、Ik(t)和Rk(t)随时间t演化的微分方程组为: 式 -(1-p)λkSk(t)θ(t)-p(1-α)kinfSk(t)θ(t)中,第一项表示度为k的不具有个体重视的易染节点产生新感染节点的密度。第二项表示度为k的具有个体重视的易染节点产生新感染节点的密度。βIk(t)表示感染个体以β的速率变成免疫个体的密度。 由于在传染病传播初期,度为k的感染个体的密度Ik(0)极小,可令Ik(0)≅0,所以传染病的初始条件为: 综合上述初始条件,由式(4)可得SK(t)的表达式为: 其中 式(7)两边对时间t求导,可得γ(t)的一个自洽方程为: 当系统处于稳定状态时,即t→∞时,有Ik(∞)=0,也即,而不失一般性β=1。因此可由式(8)可得: 定义 F[γ(∞)]为辅助函数。显然,γ(∞)=0 为式(9)的一个平凡解,对于一种传染病能够在网络中大范围爆发,式(9)必须存在一个关于 γ(∞)的非平凡解,即γ(∞)≠0 ,则需满足条件: 由式(9)和(10)可得: 式(11)简化可得传播阈值为: 针对BA网络中所有的易感染节点,满足个体重视度函数: 当α=0时,式(12)变成经典的SIR模型传播阈值。当 α≠0时,由于1-p+p(1-α)kinf<1,所以改进的SIR模型的临界阈值大于标准的SIR模型的阈值 改进的SIR模型,传染病的爆发程度最终为: 其中表示标准的SIR模型最终爆发程度。理论表明具有个体重视的传染病爆发规模小于标准的SIR模型的爆发规模。 因此,在无标度网络中,个体重视的引入增大了模型中传染病的传播阈值,能够有效抑制传染病的传播。具有个体重视的易染个体的比例和个体重视度与传播阈值是正相关。 理论分析已经表明考虑个体重视明显改变了传染病的传播过程。为了证明理论分析的正确性。通过数值仿真分析所提的模型在无标度网络上的传播特性。在传染病传播的初始时刻,随机选择一个节点作为感染节点。所有仿真参数如下:在BA网络中,节点总数为N=1 000,网络的初始节点数m0=3,网络增长时引进的每个新节点的最少连边数m=3,易染个体与感染个体相连被感染的概率λ=0.2,感染个体以β=1的概率被治愈。 实验1经典的SIR模型和加入个体重视度的SIR模型比较。 在实验中,当参数 p=0,α=0时表示标准的SIR模型;当参数 p=0.1,α=0.1时则表示有个体重视的SIR模型。实验随机选择一个传播个体运行50次仿真取平均值得到的被移除个体的密度R(t)随时间t的变化情况和感染个体的密度I(t)随时间t的变化情况,分别如图3和图4所示。 由图3、4可以看出,在无标度网络中,个体重视引入后传染病的传播规模显著减小,降低了传染病的传播速度,延缓了传染病高峰期的到来。意味着个体的重视度可以影响传染病的传播,对传染病传播起到抑制作用。 实验2加入个体重视度模型中,易染个体重视度一定时。 在实验中,易染个体重视度一定时(α=0.1),具有个体重视的易染个体的比例参数分别为 p=0.1,p=0.2。实验随机选择一个传播个体运行50次仿真取平均值得到的被移除个体的密度R(t)随时间t的变化情况和感染个体的密度I(t)随时间t的变化情况,分别如图5和图6所示。 由图5、6可以看出,在无标度网络中,具有个体重视的易染个体的重视度α一定时,随着具有个体重视的易染个体的比例 p增大,传染病的爆发规模显著减小,降低了传染病的传播速度,延缓了传染病高峰期的到来。意味着越多的人重视传染病,传染病就传播的越慢。 实验3加入个体重视度模型中,具有个体重视的易染个体比例一定时。 在实验中,易染个体的规模一定时(p=0.2),个体重视度参数分别为α=0.1,α=0.2。实验随机选择一个传播个体运行50次仿真取平均值得到的被移除个体的密度R(t)随时间t的变化情况和感染个体的密度I(t)随时间t的变化情况,分别如图7和图8所示。 由图7、8可以看出,在无标度网络中,具有个体重视的易染个体的比例p一定时,随着易染个体的重视度α增加,传染病的爆发规模显著减小,降低了传染病的传播速度,延缓了传染病高峰期的到来。 传染病在传播过程中受到人为因素的影响。为了分析个体重视度和具有个体重视的易染个体的比例对传染病的影响。本文提出了一种新的SIR模型,该模型充分考虑到了人们对传染病的不同态度即有些人重视传染病而有些人不重视传染病和对传染病的重视程度不一样。利用平均场理论,分析了该模型在无标度网络中的传播动力学行为。通过仿真与数值模拟,表明个体重视的引入能够对传染病的传播速度和爆发的规模起到有效的抑制作用。在传染病传播过程中可以通过增大具有个体重视的易染个体的比例或者增加个体的重视度,来抑制传染病的传播。因此,在当今信息和技术发达的社会,当传染病爆发时,政府部门应该通过各种方式来引起更多人的重视和提高个体的重视度,来抑制传染病的传播。 图3 BA网络,R(t)与t的关系(实验1) 图4 BA网络,I(t)与t的关系(实验1) 图5 BA网络,R(t)与t的关系(实验2) 图6 BA网络,I(t)与t的关系(实验2) 图7 BA网络,R(t)与t的关系(实验3) 图8 BA网络,I(t)与t的关系(实验3) [1]Pei Y Z,Liu S Y,Li C G,et al.The dynamics of an impulsive delay SI model with variable coefficients[J].Applied Mathematical Modeling,2009,33(6):2766-2776. [2]Zhou T,Liu J G,Bai W J,et al.Behaviors of susceptibleinfected epidemics on scale-free networks with identical infectivity Physical[J].Physical Review E Satistical Nonlinear&Soft Matter Physics,2006,74:121-137. [3]Usaini S,Anguelov R,Garba S M.Dynamics of SI epidemic with a demographic Allee effect[J].Theoretical Population Biology,2015,106:1-13. [4]Yang J Y,Chen Y M,Xu F.Effect of infection age on an SIS epidemic model on complex networks[J].Journal of Mathematical Biology,2016,73(5):1-23. [5]Wang Y,Jin Z,Yang Z M,et al.Global analysis of an SIS model with an infective vector on complex networks[J].Nonlinear Analysis:Real World Applications,2012,12(2):543-557. [6]Liu W B,Zheng Q B.A stochastic SIS epidemic model in media coverage in a two patch setting[J].Applied Mathematics and Computation,2015,262:160-168. [7]Han D,Sun M,Li D D.Epidemic process on activitydriven modular networks[J].Physical A:Statistical Mechanics and its Application,2015,432:354-362. [8]Chen Y M,Zou S F,Yang J Y.Global analysis of an SIR epidemic model with infection age and saturated incidence[J].Nonlinear Analysis Real World Applications,2016,30:16-31. [9]Youssef M,Scoglio C.An individual-based approach to sir epidemics in contact networks[J].Journal of Theoretical Biology,2011,283(2):136-144. [10]Graham M,House T.Dynamics of stochastic epidemics on heterogeneous networks[J].Journal of Mathematical Biology,2014,68(7):1583-1605. [11]Chen L J,Sun J T.Global stability and optimal control of an SIRS epidemic model on heterogeneous networks[J].Physic A:Statistical Mechanics and its Applications,2014,410:196-204. [12]Li C H,Tsai C C,Yang S Y.Analysis of epidemic spreading ofan SIRS modelin complex heterogeneousnetworks[J].Communicationsin NonlinearScience&Numerical Simulation,2014,19(4):1042-1054. [13]Pastor-Satorras R,Vespignani A.Epidemic spreading in scale-free networks[J].Physical Review Letters,2001,86(14):3200-3203. [14]Huang Q,Min L Q,Chen X.Susceptible-infected-recovered models with natural birth and death on complex networks[J].Mathematical Methods in the Applied Sciences,2015,38(1):37-50. [15]Kang H,Lou Y,Chen G,et al.Epidemic spreading and global stability of a new sis model with delay on heterogeneous networks[J].Journal of Biological Systems,2015,23(4):557-595. [16]Liu C,Xie J R,Chen H S,et al.Interplay between the local information based behavioral responses and the epidemic spreading in complex networks[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2015,25(10):103-111. [17]Meloni S,Perra N,Arenas A,et al.Modeling human mobility responses to the large-scale spreading of infectious diseases[J].Scientific Reports,2011,62(1):1-7. [18]Li T,Liu X D,Wu J,et al.An epidemic spreading model on adaptive scale-free networks with feedback mechanism[J].Physical A Statistical Mechanics& Its Applications,2016,450:649-656.
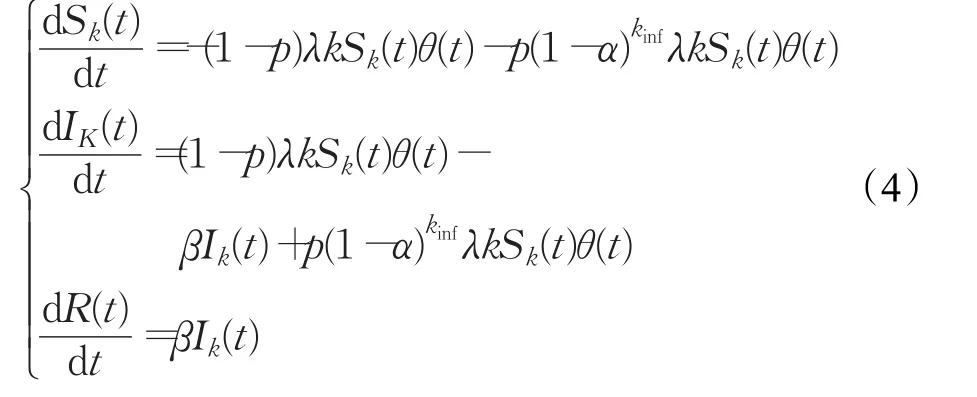


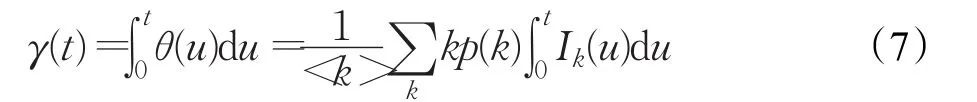
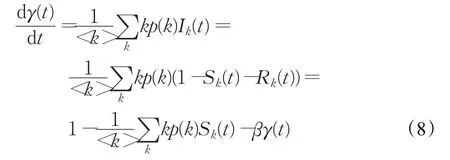
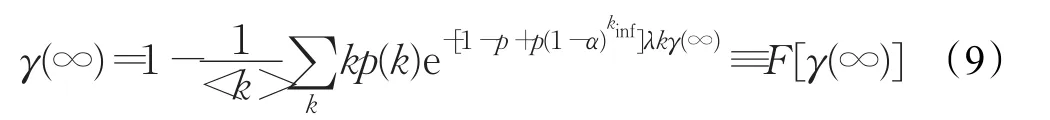

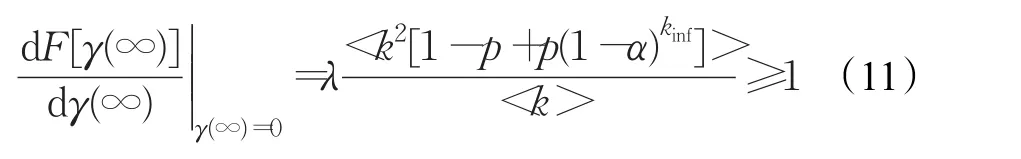
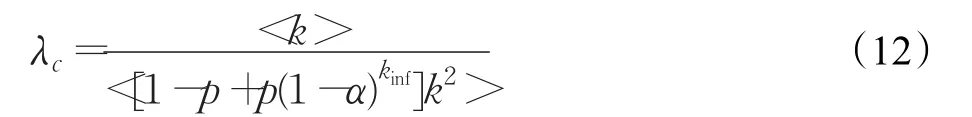
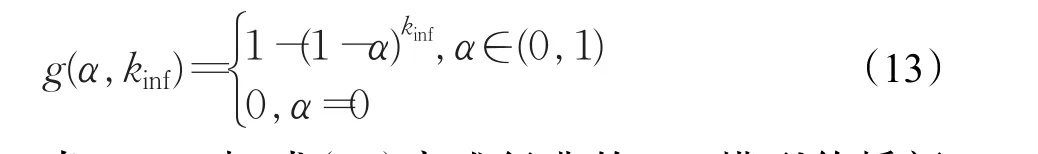

3 仿真结果与分析
4 结束语