船舶发电柴油机冷却腔内沸腾两相流数值模型研究

花仕洋，杨 杰，王 傲，詹东旭



船舶发电柴油机冷却腔内沸腾两相流数值模型研究

花仕洋，杨 杰，王 傲，詹东旭

（武汉船用电力推进装置研究所，武汉 430064）

现代船舶发电柴油机冷却系统设计趋势朝着小型化、整凑型发展，沸腾传热因高效换热能力而备受关注。本文以CFX欧拉双流体模型为基础，通过CCL语句添加用户自定义程序实现对低压系统时矩形通道内过冷流动沸腾的数值模拟。采用Kurul和Anglart修正的过冷度线性关系描述气泡直径；通过改进封闭方程以及经验式，进而改善模型计算收敛性和精度，对不同流动参数下矩形通道内过冷沸腾两相流进行实验与计算对比。计算结果表明随着壁面热流的增加气相体积分数增加；通道质量流量增加气相体积分数下降。该数值模型的建立可为真实船舶发电柴油机冷却水腔沸腾两相流分析奠定基础。

过冷沸腾 两相流 双流体模型 空泡率

0 引言

过冷沸腾发生于受热壁面温度高于当地液体饱和温度而主流体温度低于饱和温度的情形，大量的热量通过壁面迅速传递给流动液体并未造成受热壁面温度的大幅增长。近年来研究发现，大功率船舶发电柴油机缸盖的冷却水腔中存在着过冷沸腾现象[1]，特别随着现代柴油机冷却系统设计趋势朝着小型化，紧凑型方向发展，柴油机局部热负荷会越来越高[2]。在气缸盖热关键鼻梁区域出现局部的过冷沸腾已不可避免，且沸腾传热量占当地换热总量份额越来越高。另一方面，采用过冷沸腾传热方式有助于提高局部换热能力，强化柴油机冷却散热，是未来柴油机的冷却系统的发展方向[3,4]。然而，关于柴油机冷却水腔内复杂流动的沸腾传热机理模型的研究目前还不够成熟，模型适用性有待验证。为了能更好地将沸腾技术运用于柴油机冷却系统中，提高整机散热效率，亟需开发出一套过冷沸腾传热数值模型并拥有良好的适用性，用来准确预测冷却系统内的流动及沸腾状况，正确指导工程缸盖水腔开发设计。本文以计算流体力学软件CFX欧拉双流体模型为基础，通过CCL语句添加用户自定义程序实现对低压规则矩形通道内过冷流动沸腾的数值模拟，为后期真实柴油机冷却水腔沸腾两相流分析奠定基础。

1 基本数学理论

1.1壁面沸腾传热模型

壁面热流的分配决定着加热表面附近的相间传质，众多低压过冷流动沸腾的实验和理论研究[5,6]表明，壁面热通量有三个组成部分，即：

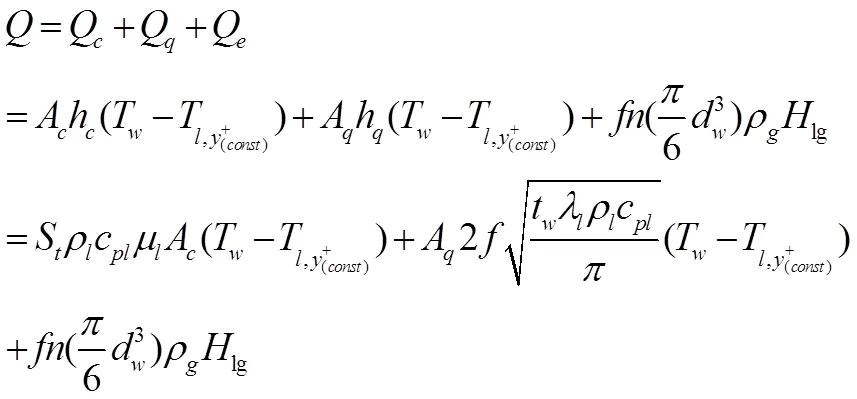
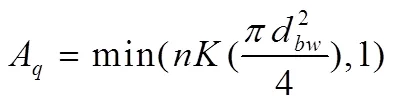
1.2相间传质模型

在过冷沸腾中，相间的传热传质是通过气泡在加热面的蒸发和气泡在过冷液中的冷凝来完成。在加热面上蒸发形成起泡后，气泡会脱离加热面，被过冷液体围绕，从而气泡发生冷凝，逐渐变小消失。在CFX中，相间传热引起的相变过程可以由热相变模型来模拟。

在加热面的壁面处，每单位体积的蒸发率Γgl[7]可以表示为：

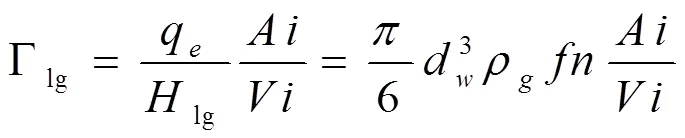
其中Ai和Vi分别表示第i个近壁网格的加热面面积和体积。

冷凝引起的传质速率Γlg[8,9]可表示为：

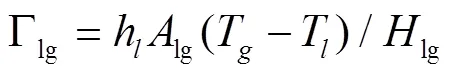
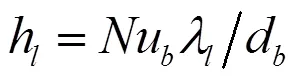
1.3相间动量传递

由于每个单独的物理现象相当于有一个对应的力作用的影响，假定界面力是不同单独物理现象对应作用力的总和。总界面力包括曳力和非曳力，在本文中，非曳力主要考虑升力、虚拟质量力、壁面滑移力、湍流耗散力。

相间曳力是由于液相与气相之间相对运动的界面间摩擦和作用在气泡上的不同压力引起的，相当于气泡在流体中受的阻力，曳力的方向与气泡相对运动的方向相反，曳力大小取决于气泡的形状和大小，文中采用Ishii-Zuber模型[8]来描述该曳力。

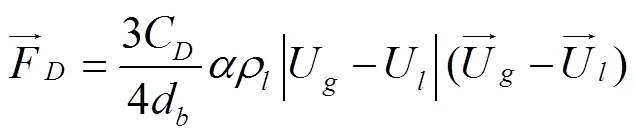
其中d为气泡直径，C为曳力系数。

升力对准确预测垂直壁面方向的空泡率分布起着很重要作用，受近壁处的连续相的速度旋度影响，其与液相的密度成正比，该作用力方向垂直并远离壁面。升力计算公式如下：

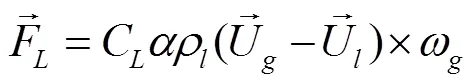
其中C为升力系数，工程中通常取值为0.1-0.5，具有很大的经验性[8]。本文采用Tomiyama[9]拟合的升力系数，以增加过冷沸腾模型的适用性，为今后应用到其他复杂模型做准备。

壁面滑移力一般只作用在近壁薄层已经脱离壁面的气泡，使其远离加热面，防止气泡附着在壁面区域，作用距离很短，通常被定义为：

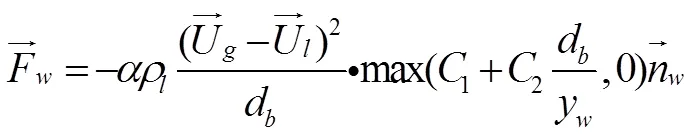
湍流耗散力是由相间曳力和湍流漩涡共同的相互作用而产生，使集中的气泡从较高浓度区逐渐向较低浓度区扩散，考虑将来应用到复杂工况及通道系统中，这里采用Favre曳力平均关系式[8]：

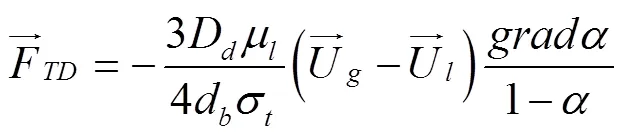
其中σt液相水的湍流施密特数，取值为0.9，由于蒸汽泡密度与水的密度相差较大，本文引入虚拟质量力，其计算式为：

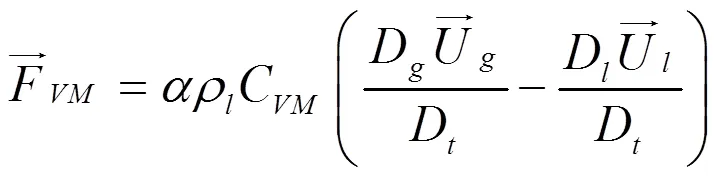
式中C是虚拟质量力系数，其取值为0.5。

1.4方程封闭子模型

在RPI模型中的壁面气化核心密度采用Egorov和Menter提出的模型[10]：

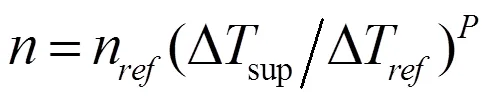
其中，n和∆T推荐值分别为n=0.8x9.922e5[m-2]和∆T=10K,取值1.805,∆T为壁面过热度。

气泡脱离频率则采用Cole提出的关联式[8]：

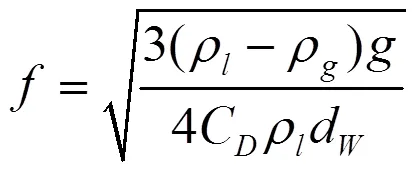
其中C是曳力系数，在本文中取值为1.0

在两相流中，气泡脱离直径一直是一个非常重要的参数，该参数直接影响到预测的准确性，常用有Tolubinskiy关联式[11]：

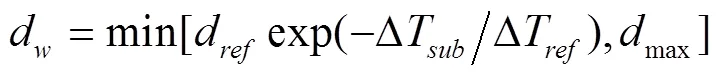
该气泡脱离直径及其上限是以高压环境下的实验数据统计总结的。随后Unal提出的一个压力使用范围广的模型，该模型低压下同样适用，但是该模型预测的是入口段的气泡脱离直径。Unal表达式如下，适用范围：压力：0.1< P < 17.7 MPa；壁面热流密度：0.47 H为潜热,U为近壁区域的气泡流动速度，取U=0.61m/s,U为液相主流体流速。

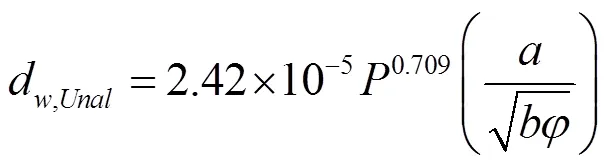
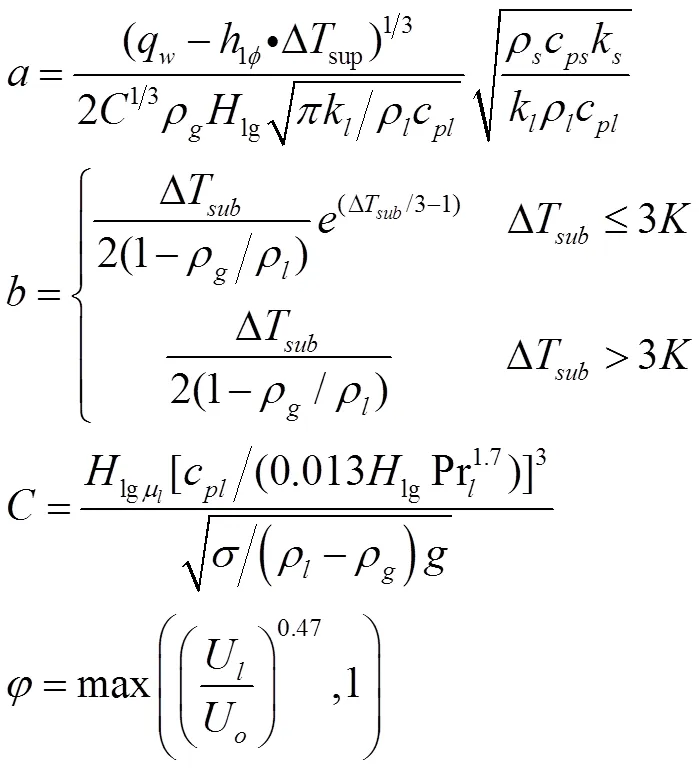
为了建立低压环境下的过冷沸腾传热模型，本文基于Tolubinsky的关联式，用Unal提出的气泡脱离直径给予修正。用Unal气泡脱离直径作为Tolubinsky气泡脱离直径的参考直径，并对参考过冷度给予修正，表达式如下所示：

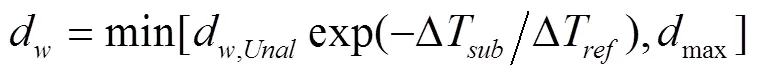
此外，气泡的直径决定了界面的大小和界面力的大小，直接影响相间动量交换以及传热传质。通过实验测量，气泡直径在远离加热面的方向上先是增大，然后在主流体区域达到最大值，然后冷凝变小最后消失。由于缺乏和气泡直径相关的原始实验数据，很多学者都假设气泡直径为一个常数，用一个常数来描述气泡大小，由于在低压下气泡直径要比高压下的尺寸大，所以气泡直径一般取1mm到4mm。Kurul，Podowski和Anglart，Nylund为气泡直径建立了一个与过冷度相关的线性函数关联式

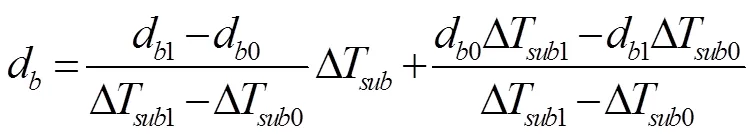
其中最小气泡直径d和最大气泡直径d分别是在过冷度∆T和过冷度∆T对应的值。

2 实验来源与模型验证

2.1实验数据来源

本文以德国慕尼黑工业大学的Maurus[14]等人发表的实验数据为基础，该实验段通道为一截面为40 mm×40 mm，长为500 mm的矩形通道。加热块为紫铜材质，位于实验段的下游底部，其尺寸为200 mm×15 mm，距离入口处250 mm处。采用纯水为工质，在该实验中，系统压力维持在0.11 MPa，工质入口过冷度为20 K。在不同比质量流速和不同的热流密度下进行相关实验。

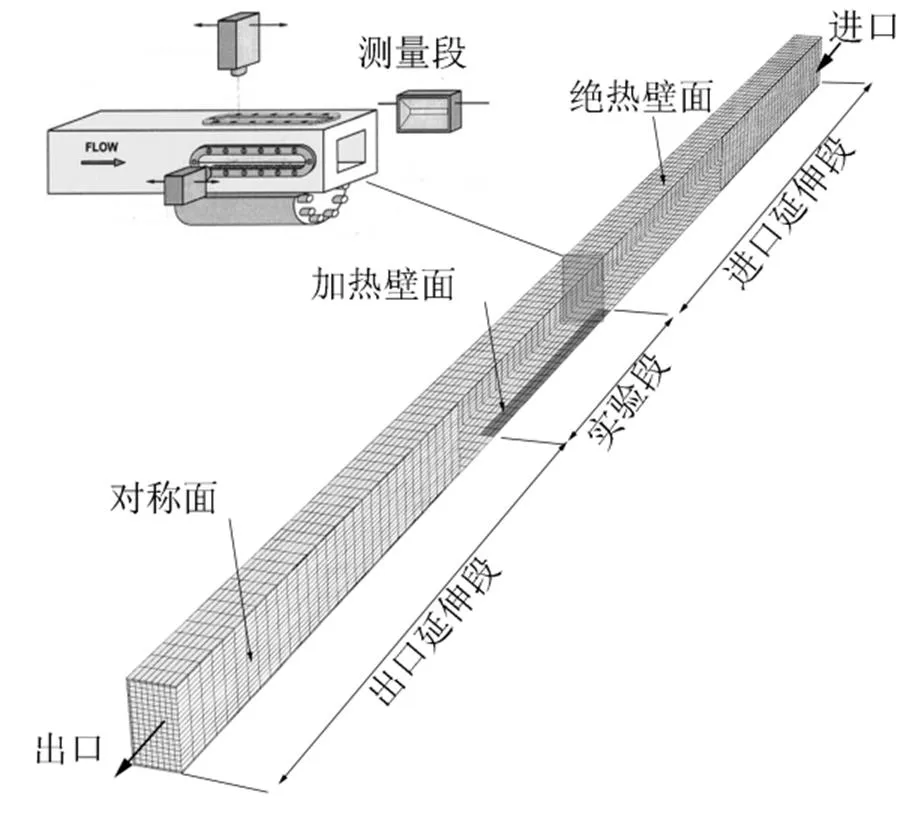
图1 实验通道示意图

2.2模型验证

如图2所示，采用Tolubinsky气泡脱离直径、Unal气泡脱离直径、修正后的气泡脱离直径计算显示，在Pos_a加热面处垂直方向的局部空泡率相差明显。工况=0.48 MW/m^2，=500 kg/m^2s时和工况=0.77 MW/m^2，=500 kg/m^2s时，修正后的子模型计算结果均有改善。还可看出，高压下的Tolubinsky气泡脱离直径应用在低压下的矩形通道内，计算空泡率分布普遍偏小。低压Unal气泡脱离直径子模型相比Tolubinsky模型，通道空泡率预测偏差有所改善，但仍处于偏低的水平，这是由于Unal气泡脱离直径没有与局部流动参数进行关联。修正后的新气泡脱离直径模拟出的空泡率分布与实验值更为接近，后续计算case均采用新模型进行计算分析。

3 计算结果与分析

3.1 气相分布云图

在比质量流量为250 kg/m^2s，不同热流密度下，对称面处的气相分布如图3(a)所示，在图中可以看出：气泡主要集中在距离加热面很近的区域；在比质量流量一定的情况下，随着加热面热流密度的增大，空泡率越来越大，气泡区域也越来越大。图3(b)表示在工况G=375kg/m^2s，q=0.27 MW/m^2下，在加热面段通道内的气相分布情况，沿着加热面方向，最大空泡率逐渐增大，气泡所占区域也逐渐扩大。

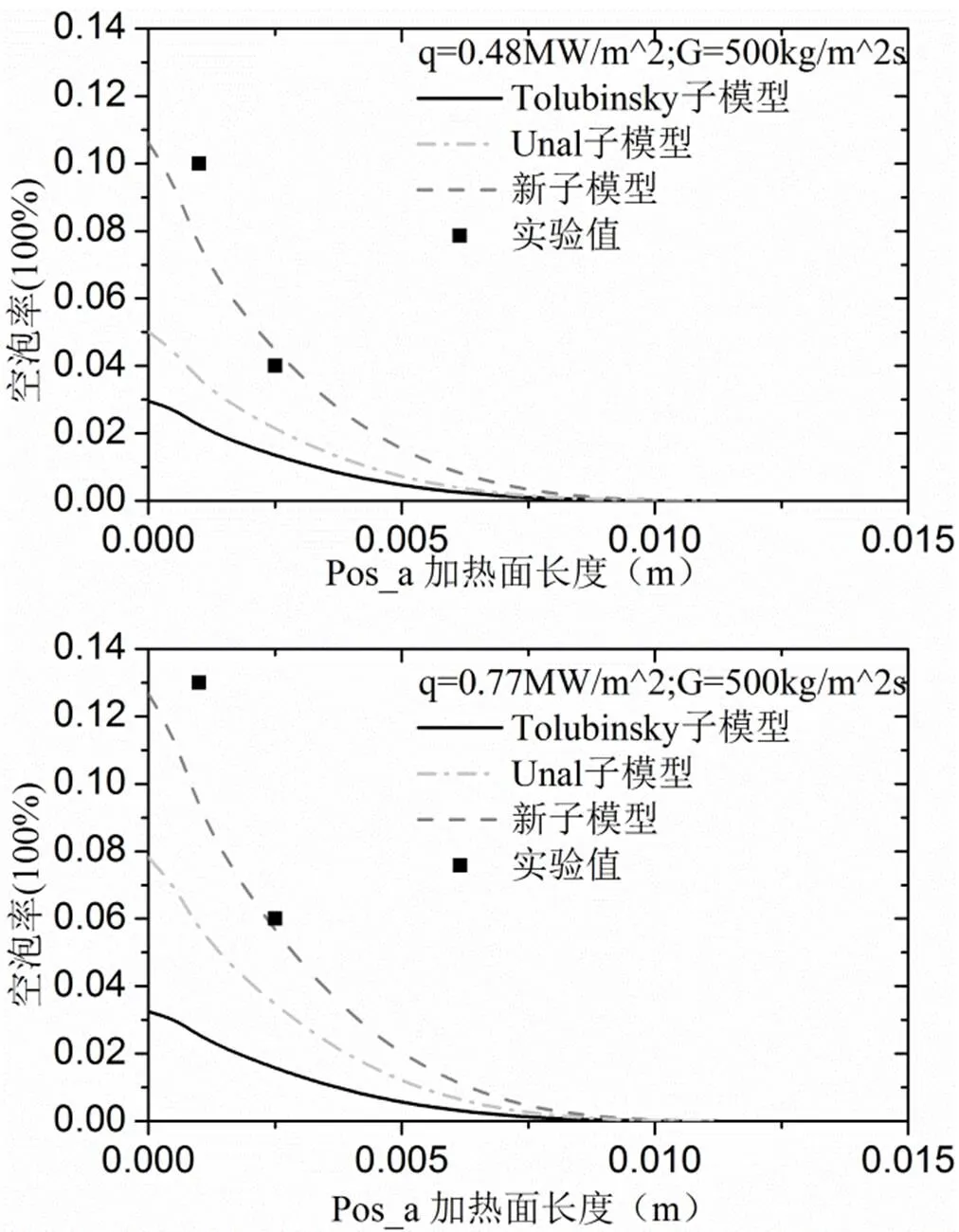
图2不同气泡脱离直径子模型对局部空泡率影响

图3(a)对称面处的气相分布云图

(b)通道内的气相分布云图

3.2壁面热流密度对空泡率的影响

图4表示在Pos_a处部分实验值与模拟值对比结果。可以看出，在比质量流量一定时，空泡率随着热流密度的增大而增大。这主要是因为，流速不变时热流密度增加，壁面过热度增加，在壁面处会产生更多的气泡，同时热流密度的增加还会使近壁面区域的液体温度升高，则气泡冷凝速度降低，气泡占的份额会增多，即空泡率增大。

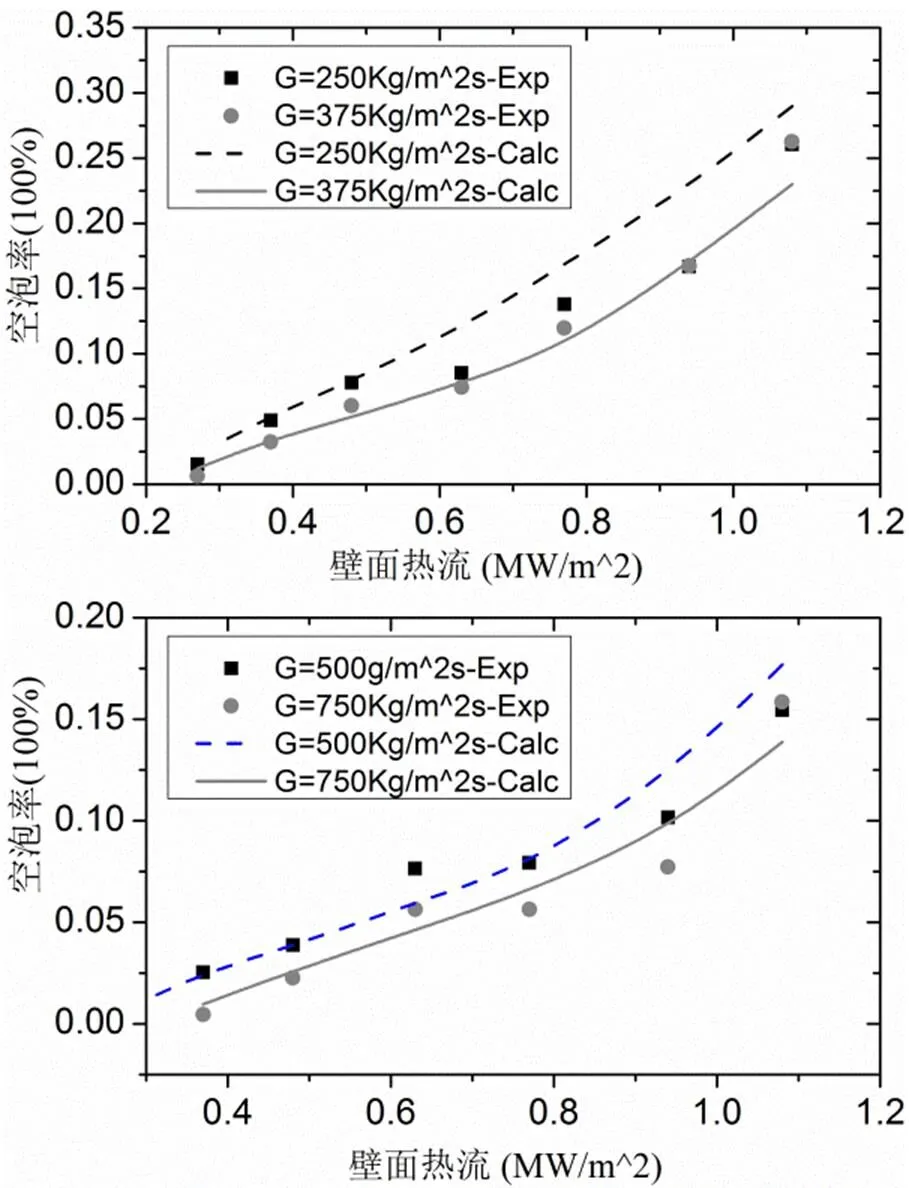
图4热流密度对空泡率影响

3.3比质量流量对空泡率的影响

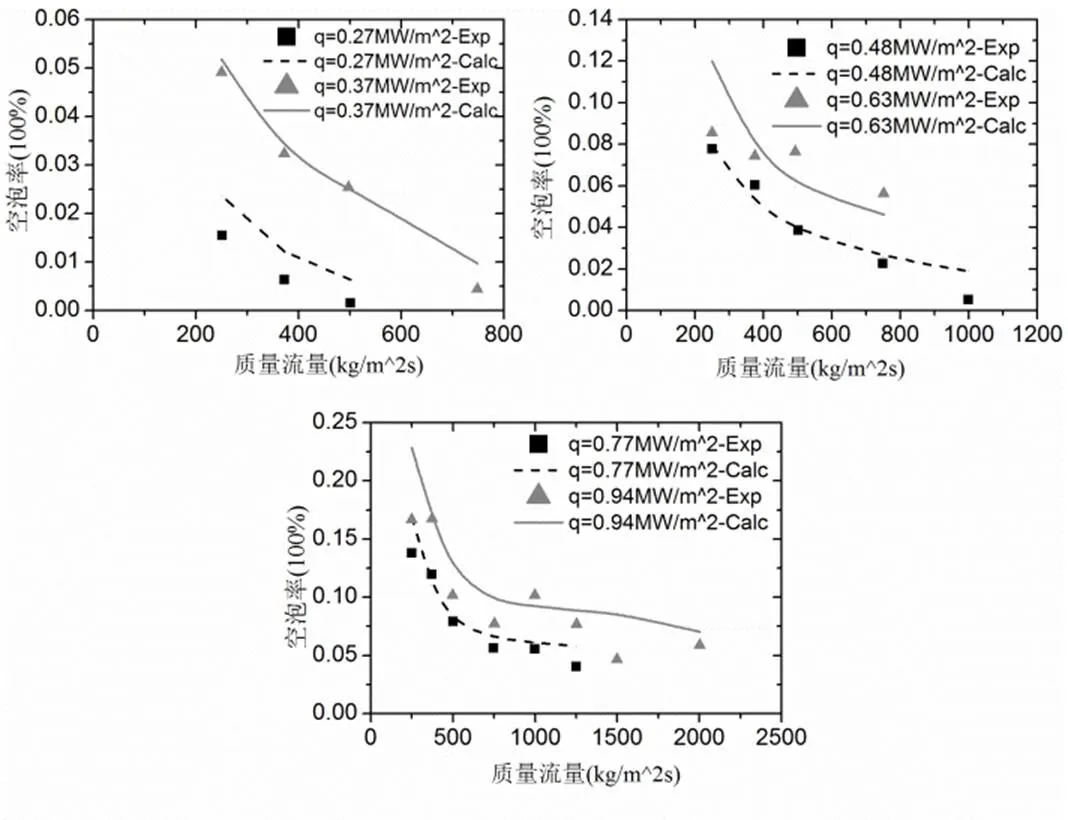
图5比质量流量对空泡率的影响：实验值与模拟值

在图5中反映了不同的比质量流量下，空泡率模拟值与试验值得对比情况。可以看出，热流密度保持不变，空泡率随着质量流量的增加而减少。这是因为流速的增加，液相加热时间变短，则近壁区域的液相的温度降低，这样脱离壁面的气泡会加速冷凝，气泡很快消失，因此气泡空泡率会随着比质量流量的增加而降低。此外，通道质量流量越大，流动扰动越强，气泡与主流体之间的作用越强烈，气相越容易被携带走或被冷凝。

3.4不同实验段位置的气相分布

图6是在壁面热流密度=0.48 MW/m^2下，不同实验测量位置处空泡率实验值与计算值的对比。可以看出，计算结果与实验基本吻合，在靠近加热面开始端的区域，通道空泡率较低，沿着加热面方向，由Pos_a位置逐渐接近Pos_c位置时，通道空泡率逐渐增大。同时可以看出，在高质量流量时，计算结果与实验值相差较远，其原因是高流速时，气泡相间作用关系更为复杂，需要进一步完善封闭子模型。

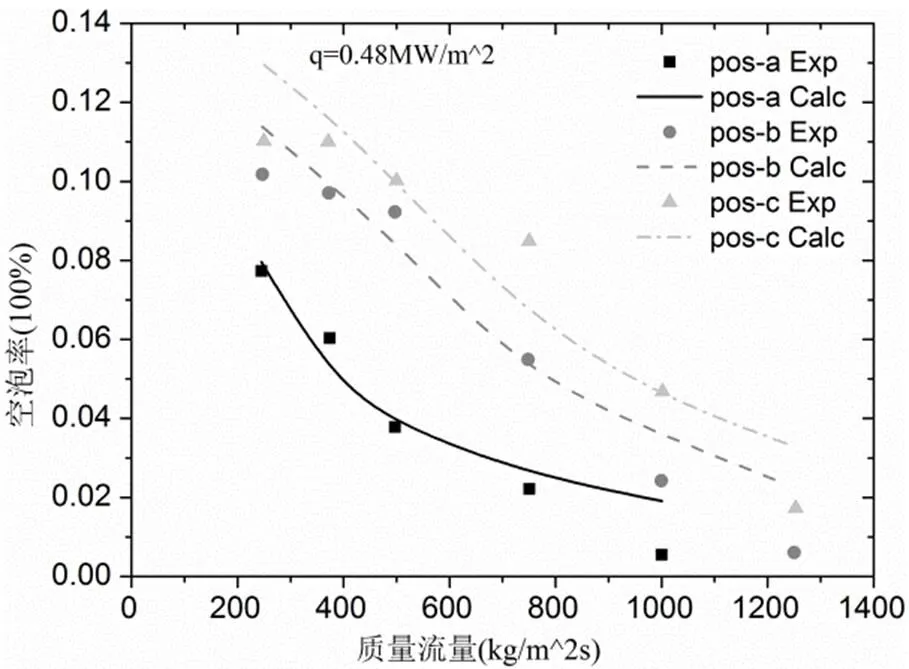
图6不同位置的空泡率随比质量流量变化情况

4 结论

1）采用修正后的Tolubinsky关系式作为汽泡脱离直径和与过冷度线性关系的气泡直径，计算结果与实验值吻合较好，并采用Tomiyama升力关系式与Favre曳力关系式，弥补升力系数和湍流耗散力经验系数需要调整的不足。

2）当只有热流密度变化时，空泡率则随着热流密度的增加而增加；当只有流速变化时，空泡率则随着流速的增加而降低。

3）通过矩形通道内低压过冷沸腾实验数据的对比，验证了该模型的适用性，为今后应用到其真实柴油机复杂冷却通道的过冷沸腾分析奠定了基础。

[1] 刘永,李国祥,付松,石秀勇,白书战. 一种适用于缸盖水腔沸腾传热计算的模型[J]. 内燃机学报, 2008,01:76-82.

[2] 何联格,左正兴,向建华. 气泡尺寸对气缸盖沸腾换热的影响[J]. 内燃机学报,2013, (01):72-77.

[3] 董非，郭晨海，等.发动机冷却水腔内沸腾传热的模拟研究[J].内燃机工程，2011, 32 (4):76-82.

[4] K.Robinson,N.A.F.CamPbell,J. and D.G.Ti11ey.A Review of Preeision Engine Cooling[C]//SAE Paper1999-01-0578.

[5] Tu J Y, Yeoh G H. On numerical modelling of low-pressure subcooled boiling flows[J]. International Journal of Heat and Mass Transfer, 2002, 45(6): 1197-1209.

[6] F. R. Menter. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications [J]. AIAA Journal. 1994, 32(8). 1598–1605.

[7] Kurul, N. and Podowski, M. Z., On the modeling of multidimensional effects in boiling channels[C]// ANS Proc.27th National Heat Transfer Conference, Minneapolis, MN, July 28-31, 1991.

[8] Končar B，Krepper E，Egorov Y．CFD Modeling of subcooled flow boiling for nuclear engineering applications[C]// Proceedings of the International Conference Nuclear Energy for New Europe 2005，Bled，Slovenia，2005.

[9] Chen Erfeng，Li Yanzhong，Cheng Xianghua．CFD simulation of upward subcooled boiling flow of refrigerant-113 using the two-fluid model[J]．Applied Thermal Engineering，2009，29 (11/12)：2508–2517.

[10] Egorov, Y. and Menter, F.,“Experimental implementation of the RPI boiling model in CFX-5.6”,Technical Report ANSYS / TR-04-10., 2004.

[11] V.I. TolubinskyVapour bubbles growth rate and heat transfer intensity at subcooled water boiling[C]// Fourth International Heat Transfer Conference, Paper No:B-28, Paris, 1970.

Numerical Simulation Research of Subcooled Boiling Water in a Marine Generating Diesel Engine Cooling Channel

Hua Shiyang, Yang Jie, Wang Ao, Zhan Dongxu

（Wuhan institute of Marine Electric Propulsion System, Wuhan 430064, China）

U664

A

1003-4862（2018）05-0029-05

2018-02-15

花仕洋(1988-)，男，工学博士。研究方向：船舶动力工程。