应用粗糙集和支持向量机的熔喷非织造布过滤性能预测

金关秀， 张 毅， 楼永平， 祝成炎

(1. 浙江工业职业技术学院， 浙江 绍兴 312000； 2. 浙江理工大学， 浙江 杭州 310018)

非织造布具有三维网络状多微孔结构，是优良的过滤材料[1]。材料的性能是由其内在结构所决定的，非织造布的过滤性能与其纤网结构密切相关[2-4]。用于表征非织造布纤网结构的参数有很多，如建立含所有纤网结构参数的方程体系来研究结构对其过滤性能的影响，但因其工作量过大而不适于实际应用。因此有必要提取尽可能少的参数来建立预测模型。此外非织造布纤网结构参数与过滤性能之间呈现复杂的非线性关系，但又具有其内在规律性，利用传统方法如线性回归分析等统计技术已难以呈现它们之间的内在关系。

熔喷非织造布纤维直径小，比表面积大，是一种较为理想的过滤材料。本文运用粗糙集对熔喷非织造布纤网结构参数进行降维，得到最能够表征纤网结构特征的核心参数，并利用支持向量机建立预测模型探讨熔喷非织造布结构参数对其过滤性能的影响，从而为研制高效低阻的多层复合非织造空气过滤材料提供理论基础。

1 纤网结构与性能

本文选取30块聚丙烯熔喷非织造布作为研究对象，样品均来自浙江理工大学先进纺织材料与制备技术教育部重点实验室。采用9个参数对熔喷非织造布的纤网结构特征进行描述，即面密度、厚度、纤维直径、纤维直径变异系数、基平面网特征长度、取向因子、孔隙率、孔径以及孔径变异系数。

1.1 面密度测定

按照GB/T 24218.1—2009《纺织品 非织造布试验方法 第1部分：单位面积质量的测定》，采用AL204-IC型电子天平测试样品面密度。

1.2 厚度测定

按照GB/T 24218.2—2009《纺织品 非织造布试验方法 第2部分：厚度的测定》，采用YG(B)141D型数字式织物厚度仪测试样品厚度。

1.3 纤维直径及其变异系数测定与计算

采用JSM-5610LV型扫描电子显微镜(SEM，日本JEOL公司)采集样品的图像，放大倍数为1 500，每个样品取10个不同部位进行扫描获取图像。图1示出样品的SEM照片，图像大小为420像素×420像素。用Image Pro-Plus软件测量各个样品不同SEM图像中100根纤维的直径，并求取平均值d(μm)与变异系数CVd(%)。

图1 样品SEM照片(×1 500)Fig.1 SEM image of sample (×1 500)

1.4 基平面网特征长度计算

最简单的纤维网是由相互交叉的若干根纤维所构成，通常称之为基平面网，非织造材料可认为是由若干个基平面网叠加而成的纤维集合体[5]。基平面网特征长度按下式计算：

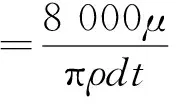
(1)

式中：σ为基平面网特征长度，m/m2；ρ为纤维体密度，g/cm3；μ为样品面密度，g/m2；t为样品厚度，mm。

1.5 取向因子测定

本文采用直接测角法测定纤网的取向程度，将纤维与熔喷非织造布纵向的小于或等于90°的夹角之平均值定义为纤维平均取向角，记为α。具体操作方法为运用Image Pro-Plus软件对样品SEM图像中的纤维取向角进行标定，每个样品均测取10幅SEM中的所有纤维的取向角，求取平均值。显然，α值越接近45°，纤维排列杂乱程度越高。

设f为熔喷非织造纤网的取向因子，其计算公式为：

f=cos2α

(2)

可见，f值越大，纤网的取向程度就越高。

1.6 孔隙率计算

熔喷非织造布孔隙率按下式进行计算：

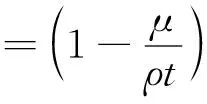
(3)

式中φ为孔隙率，%。

1.7 孔径及其变异系数测定与计算

采用PSM165孔径测试仪(德国Topas GmbH公司)测取样品的孔径P(μm)及其标准差，并据此计算孔径变异系数CVp(%)。

1.8 过滤性能测试

采用美国TSI公司生产的TSI-8130自动滤料测试仪(气溶胶为石蜡油型)，测试30个样本的过滤效率和过滤阻力。每个样本取10个不同部位进行测试。

2 过滤性能预测与分析

2.1 属性约简

粗糙集理论通过对知识的形式化定义，可从不完备数据中发现隐含的知识，探明潜在的规律，进行知识的简化——属性约简[6-7]。

所谓属性约简，就是在所有条件属性构成的集合中，抽取可以尽量多地保留属性全集的分类信息的属性子集的过程[8]。本文通过属性约简可以提取出熔喷非织造布纤网结构参数全集中最能够代表纤网结构内在特征的参数子集。与其他数据降维技术如因子分析、聚类分析等相比，属性约简的优势在于降维结果完全保留了变量的原始形式，有利于某些必须依赖原始变量的后续研究。

30个熔喷非织造布样品的纤网结构参数的测试结果如表1所示。然后求取平均值，表2示出过滤性能测试结果。表中FE表示过滤效率，%；ΔP为过滤阻力，Pa。对表1中原始数据(属性值)采用等距离法进行离散归一化处理。设步进量Astep=(Amax-Amin)/3(Amax表示每一列的最大值；Amin表示每一列的最小值)。将每一列的属性值分成3个等级：原始数值在(Amin+2Astep) 与Amax之间的归为2；原始数值在(Amin+Astep) 与(Amin+2Astep) 之间的归为1；原始数值在Amin与(Amin+Astep) 之间的归为0。表3示出属性值离散化的结果，其中0、1、2即为原始数据的离散化值。

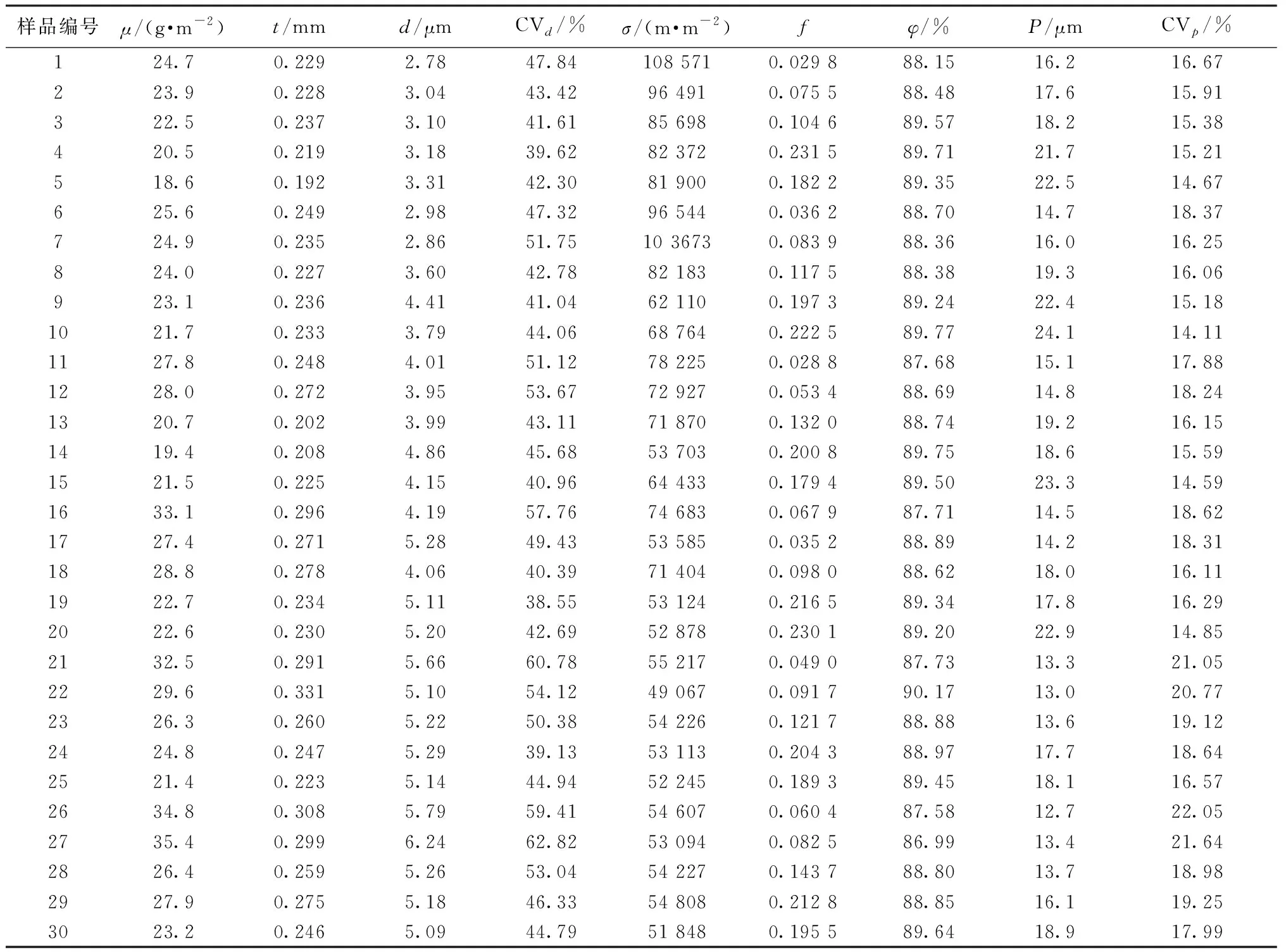
表1 纤网结构参数测试结果Tab.1 Test results of fiber web structure parameters

根据粗糙集理论，知识库中的知识(属性)并不是同等重要的，并且还存在冗余。本文运用ROSETTA软件采用遗传算法进行属性约简。遗传算法模拟生物在自然环境中的遗传、进化过程，系一种自适应全局化概率搜索算法，具有鲁棒性、隐含并行性和全局搜索等优点。将遗传算法引入粗糙集属性约简中，可减少计算的复杂性，求出最小相对约简或近似最小相对约简。实施约简前对离散化后数据作相容性检查，从表3可以发现样品5、7、15、25、26、27、28的属性值经离散化后属于重复信息，即5的离散化值与4相同；7的离散化值与1相同；15的离散化值与9相同；25的离散化值与19相同；26、27的离散化值与21相同；28的离散化值与23相同，在进行属性约简时应予以删去。

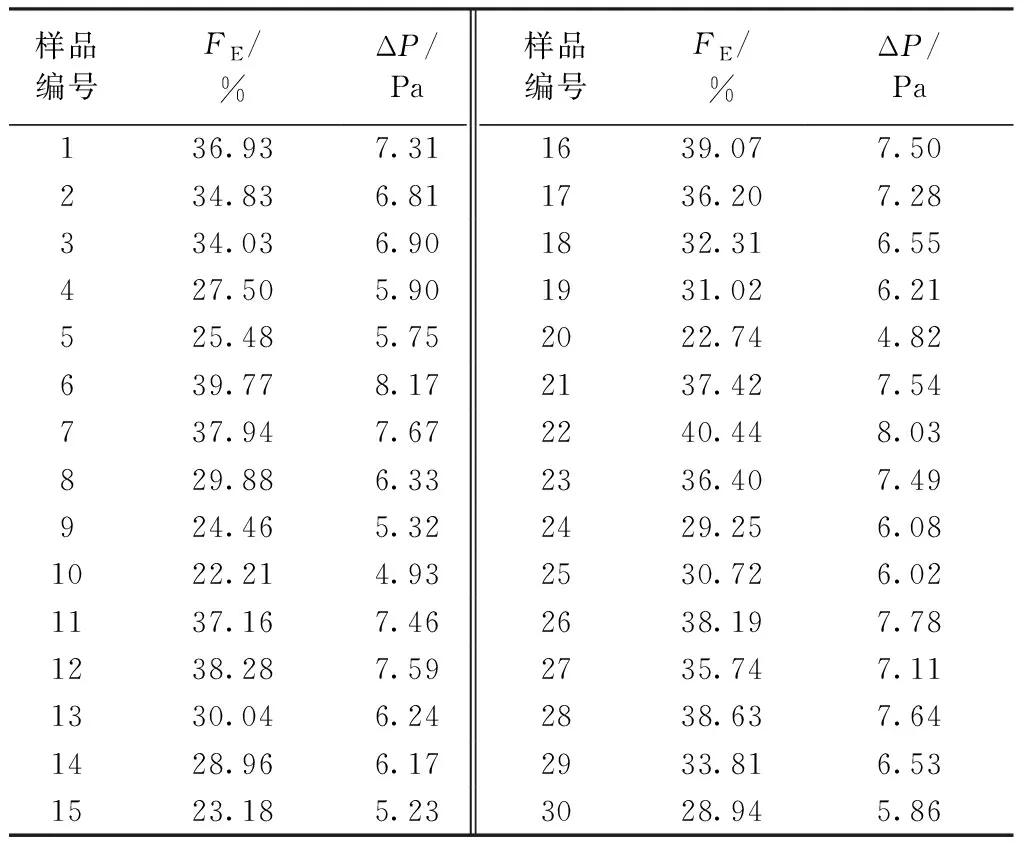
表2 过滤性能测试结果Tab.2 Test results of filtration performances

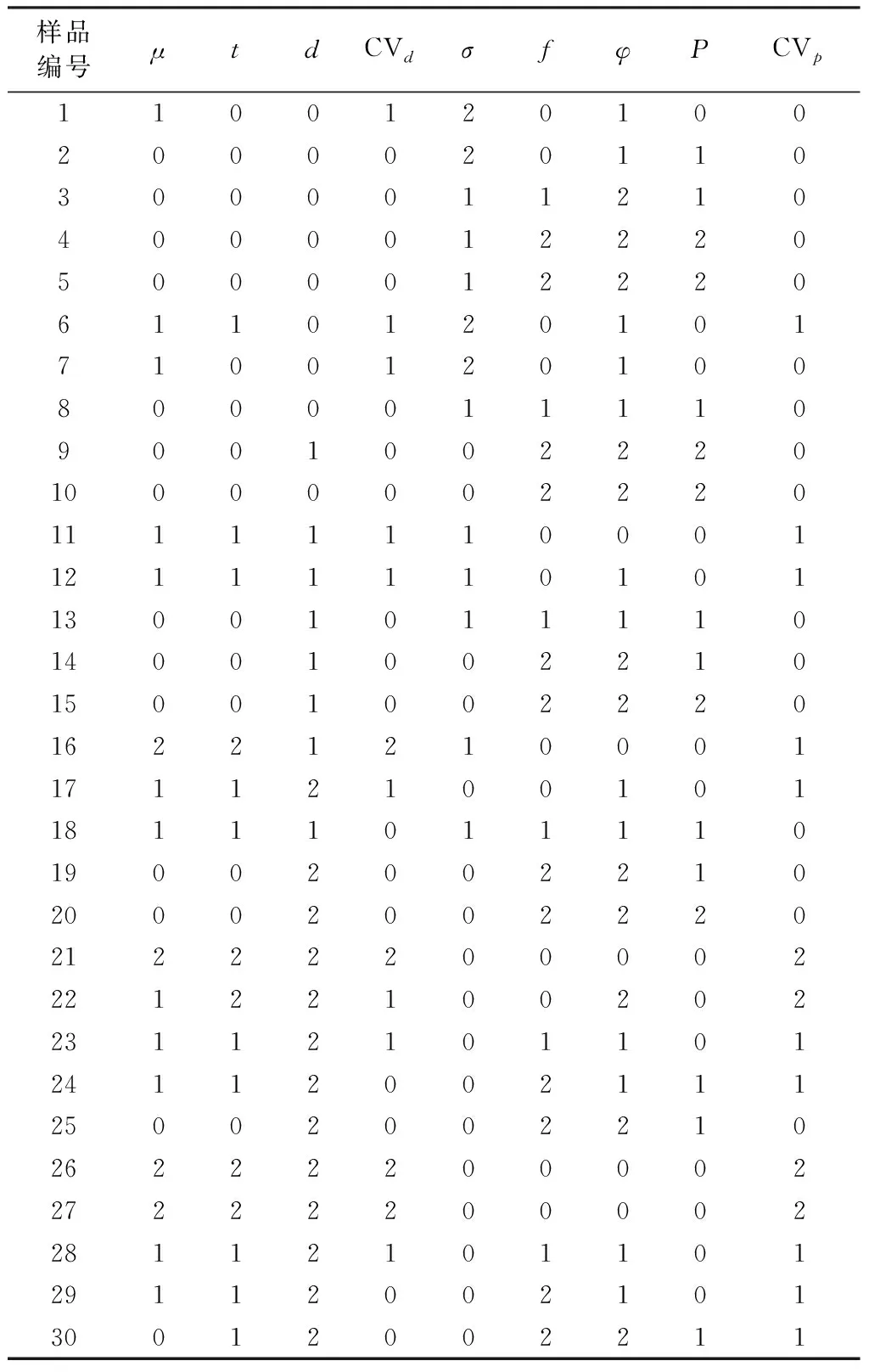
表3 属性值离散化结果Tab.3 Discrete normalization result of attribute values

设S为未经约简的结构参数全集，在ROSETTA环境下S通过约简得到的最小相对约简(以下简称约简)有6个，以Ri代表第i个约简(i=1, 2, 3, 4, 5, 6)，则：

由式(4)可知，在S中被认为是冗余的纤网结构参数有：面密度μ、孔隙率φ和孔径变异系数CVp。分析认为，μ可根据式(1)由t、d和σ推导出；φ可根据式(1)和式(3)由d和σ推导出，即结合式(1)、(3)可得：

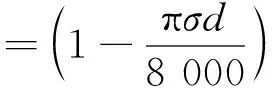
(5)

此外，从表1可知，30个熔喷非织造布样本的孔径变异系数CVp数值本身不是很大，且波动范围(14.11%～22.05%)也不是很大，使其在整个属性信息系统中的地位显得不突出，这可能是它在属性约简中被认为是冗余的原因。

2.2 预测模型及其参数优化

2.2.1预测模型

采用MatLab编程，将上述6个约简(R1,R2, …,R6)连同未经约简的结构参数全集S作为支持向量机或BP神经网络的输入，对熔喷非织造布的过滤性能进行预测，同时通过各个模型预测准确度的分析比较，识别出影响过滤性能的核心纤网结构参数子集。

支持向量机(SVM)算法的基本原理为通过内积核函数定义的非线性变换将输入空间变换至一个高维空间，以探寻输入和输出变量之间的某种非线性关系。SVM遵循结构风险最小化原理，在小样本的情况下仍具有良好的泛化能力[9]。BP神经网络(BP-ANN)是一种按误差逆传播算法训练的多层前馈网络，具有并行处理速度快、容错性强、计算简单等优势。无论是基于SVM的模型还是基于BP-ANN的模型，均有过滤效率和过滤阻力2个输出，由此共计建立了28个熔喷非织造布过滤性能预测模型，图2示了预测模型结构图。本文采用交叉验证法进行模型的训练和预测。

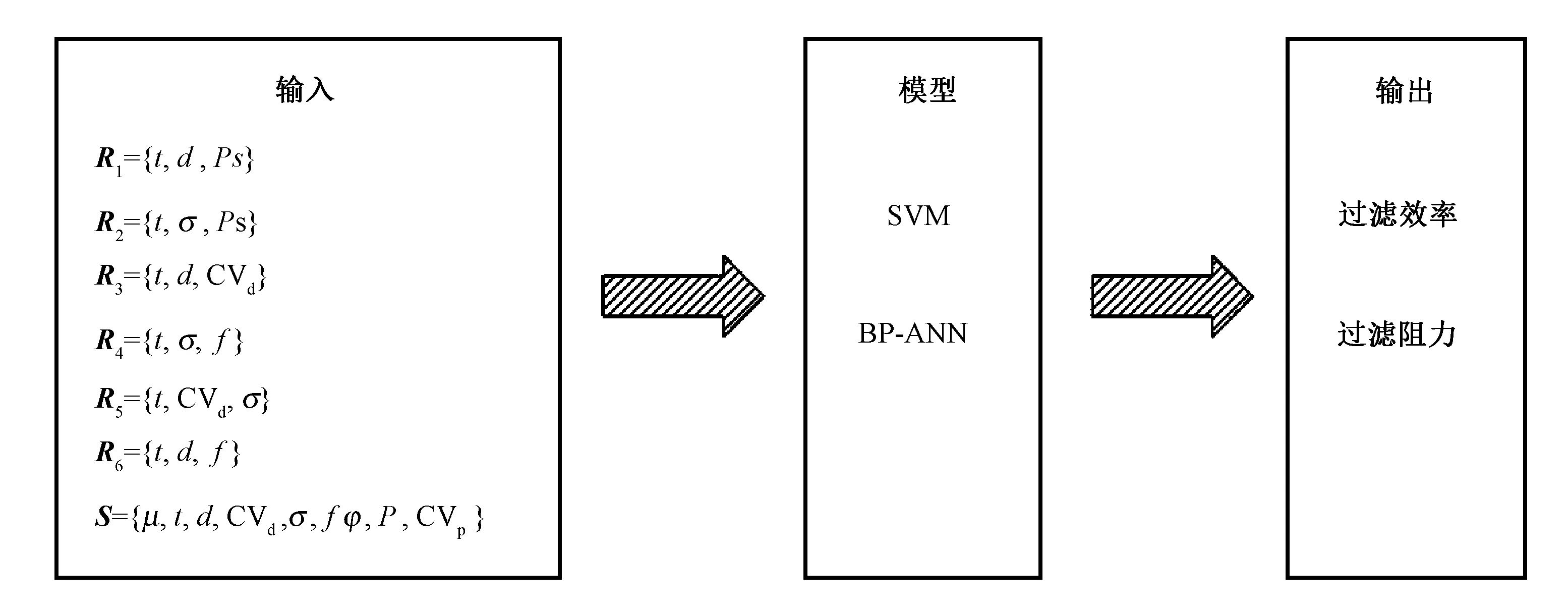
图2 预测模型结构图Fig.2 Structure of prediction model

2.2.2参数优化

SVM模型以径向基函数(RBF)为核函数，运用10折交叉验证法对每个模型的参数包括RBF的宽度B、惩罚因子C和不敏感系数ε进行优化。BP-ANN的主要结构参数包括隐含层数量和每个隐含层中的神经元数目。研究中采用1个隐含层的BP-ANN，转换函数为正切S型函数[10]，运用10折交叉验证法对每个模型的隐含层神经元数目进行优化。模型参数优化的结果如表4所示。

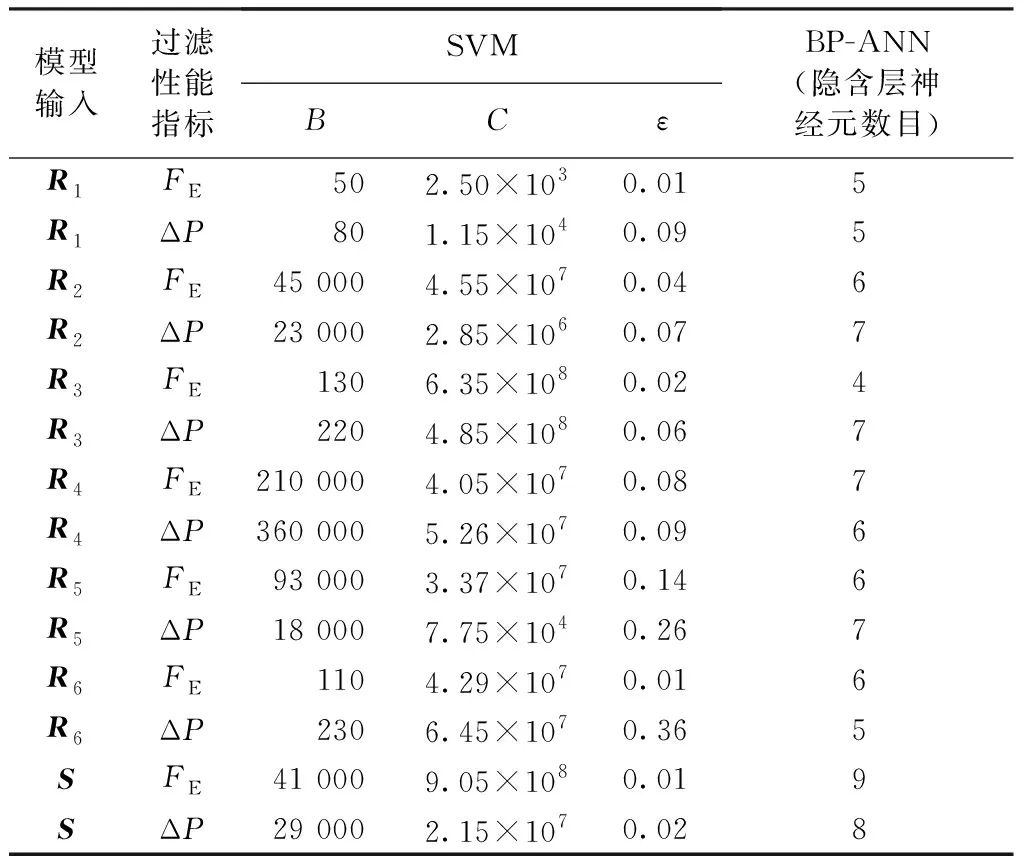
表4 模型参数的优化Tab.4 Optimized parameters of models

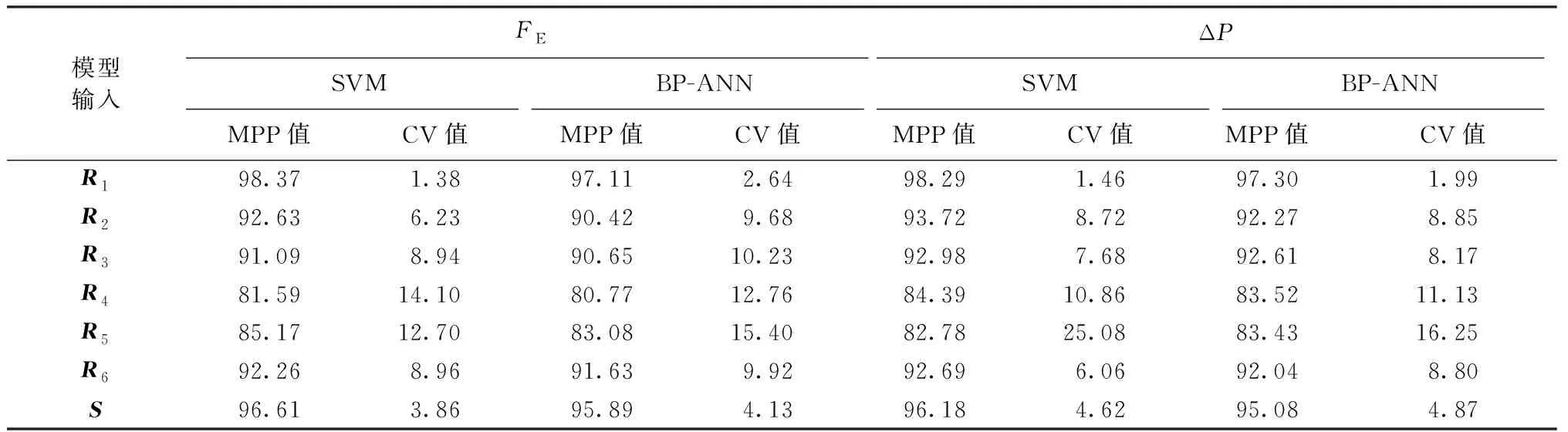
表5 模型的预测准确性Tab.5 Prediction accuracy of models %

2.3 预测模型准确性分析

本文以预测精度PP(prediction precision)及其变异系数(CV)来表征模型的预测准确性，PP值按下式计算：

(6)

式中：o为样本实测值；p为样本预测值。表5示出各模型的预测准确性，其中MPP表示PP的平均值。显然，MPP值越大或CV值越小，模型的预测准确度越高。一般认为，MPP值大于90%，且CV值小于10%时，模型具有较好的预测性能[11-12]。

由5表可见，以S即纤网结构参数全集为输入的模型具有较好的预测准确性，无论是基于SVM还是BP-ANN，对过滤效率和过滤阻力预测的MPP值均超过95%，CV值也均在5%以下，表明基于纤网结构参数能够对熔喷非织造布的过滤性能作准确的预测。所有模型中，以R1为输入的模型的预测准确度优于其他所有模型(包括以纤网结构参数全集S为输入的模型)，无论是基于SVM还是BP-ANN，其MPP值均超过97%，而CV值均低于3%，其中基于SVM模型的MPP值均超过98%，CV值均低于2%。这表明厚度、纤维直径和孔径这3个参数的组合是影响熔喷非织造布过滤性能的核心要素。

在以其他约简(R2～R6)为输入的模型中，以R2、R3和R6为输入模型的预测准确度为较高，无论是基于SVM还是BP-ANN，MPP值均高于90%，CV值方面，除以R3为输入、基于BP-ANN模型的数值达到10.23%外，其余均低于10%。而以R4和R5为输入模型的预测准确度相对较低，无论是基于SVM还是BP-ANN，MPP值均介于80%～90%之间，而CV值均超过10%。可以观察到，R2、R3和R6中分别含有上述3个核心参数中的2个，即R2中含有t和P、R3和R6中均含有t和d,；而R4和R5中仅含有上述3个核心参数中的1个，即t。换言之，在模型输入中含R1元素(t,d,P)的数目越多，对过滤性能的预测准确度就相对越高，这进一步验证了t、d、P是影响熔喷非织造布过滤性能的3个核心纤网结构参数。

根据经典的过滤理论，纤维材料对空气的过滤是一个动态过程，分为稳定和不稳定2个阶段，而对颗粒浓度很低的气流的过滤主要是第一阶段即稳定阶段，其特征是对微粒的捕捉效率和阻力不因时间推移而改变，而由材料的固有结构、微粒的性质和气流所决定[13]。在稳定阶段里，纤维捕集微粒的机制主要有拦截效应、惯性沉积、扩散效应、重力效应和静电效应等5种。

厚度、纤维直径和孔径对熔喷非织造布的过滤性能均存在直接的影响。熔喷非织造纤网呈多孔三维结构，材料厚度增加将导致其孔隙通道变曲折，使更多的微粒被截留，反映为材料的过滤效率越高；但同时也会使得空气阻力升高，导致过滤阻力的增大[14]。材料孔径越小，其允许通过的微粒就越少，从而过滤效率提高，但孔径减小同时也会导致空气阻力变大，使得过滤阻力也相应增大[15-16]。纤维直径减小使得纤维的比表面积增大，有助于纤维能够拦截更多的微粒，从而使材料的过滤效率上升[4,17]；而纤维直径的增大会使随机排列的纤网变得相对疏松，导致过滤阻力下降[18]。

从传统意义而言，非织造布的面密度对过滤性能具有重要的影响，但其没有被列为核心参数(在纤网结构参数属性约简时即被界定为冗余参数)。分析认为根据过滤机制，在纤维材料内部结构中对微粒进行拦截的主体是纤维，所以是由每单位体积的纤维数量、纤维本身的特性(直径、截面形状等)以及纤维的堆积形态(表现为孔隙结构)，而并不是由单位面积上纤维的质量来决定材料的过滤性能。准确地说，面密度是通过其他相关纤网结构参数间接地对熔喷非织造布的过滤性能产生影响。

研究表明，非织造布孔径数值的大小是由若干个基平面网的复合结构所决定的，而基平面网可以用3个参数σ、d和f来确立，对于刚性平直型纤维，确定孔径数值大小的基平面网个数是2[19]。构成熔喷非织造布的纤维虽属短纤维范畴，但其线密度低且长径比大，在局部范围内呈较平直状(如图1所示)，所以仍可按刚性平直型纤维分析，从而可推断，孔径和纤维直径可在一定程度上反映σ和f这2个参数所包含的信息。可以认为σ和f对材料性能的影响是通过P和d这2个参数间接地起作用。此外由式(5)可知，孔隙率可由σ和d进行推算，因此在纤网结构参数属性约简时即被界定为冗余参数。结合上述σ的信息包含P和d2个参数之中的结论，可进而推论d和P这2个参数也能够在一定程度上反映φ所包含的信息，则φ对材料性能的影响可认为是通过P和d起间接作用。

纤维直径变异系数对熔喷非织造布过滤性能具有一定的影响。CVd值越大即直径数值分布越广，小直径纤维会越多，根据过滤机制，纤维直径越小，就能拦截越多的微粒；然而CVd数值越大，同时会使得大直径纤维增多而导致过滤效率下降，因此与纤维直径d相比，CVd对过滤性能的影响较小。

孔径变异系数对熔喷非织造布过滤性能也具有一定的影响，因为占10%的大孔能带走33%的气流，因此孔径变异系数越大，过滤效率就会越低[20]。本文2.1属性约简中已述由于变异系数在整个属性信息系统中的地位不突出而被界定为冗余参数， 30个熔喷非织造布样品的孔径变异系数数值本身及其波动范围都不大，可以认为相对于孔径来说，变异系数对熔喷非织造材料过滤性能的影响是较小的。

综上所述，所有纤网结构参数都以不同的形式、在不同程度上对过滤性能产生影响，而厚度、纤维直径和孔径则是起关键作用的核心参数，其他参数或可认为是通过这3个参数间接地影响材料过滤性能(包括μ,σ,f,φ)，或对过滤性能的影响程度小于这3个核心参数(包括CVd和CVp)，因此以厚度、纤维直径和孔径这3个参数的组合作为模型输入可得到较优的预测准确度。

实验结果还表明，基于SVM模型的预测准确度总体高于基于BP-ANN的模型。由表5可见，在所有28个预测准确度数值上，基于SVM模型在25个(占总数的89.29%)数值上优于基于BP-ANN的模型，这归因于支持向量机具有更好的泛化能力和处理噪声信息的能力。

3 结 论

本文将粗糙集作为支持向量机和BP神经网络模型的前置系统，对模型的输入系统进行简化，通过属性约简减少了熔喷非织造布过滤性能预测模型中的输入变量的数量，使其下降到仅为原变量总数的1/3，从而大大提高了工作效率。对于熔喷非织造布的过滤性能而言，以厚度、纤维直径、孔径这3个参数组合而成的约简集为输入的模型预测准确度高于以其他任何约简集为输入的模型，且高于以纤网结构参数全集为输入的模型，表明它们是熔喷非织造布纤网结构参数中影响过滤性能的核心要素。SVM是基于结构风险最小化理论，其泛化能力要比神经网络强(尤其是在样本数量较少的情况下)，这一点得到本论文研究结果的支持。基于粗糙集和支持向量机的预测模型可作为熔喷非织造布过滤性能预测的新方法。

参考文献：

[1] DIPAYAN D, SHOVAN D, ISHTIAQUE S M. Optimal design of nonwoven air filter media: effect of fiber shape[J]. Fibers and Polymers, 2014, 15(7): 1456-1461.

[2] JACKIEWICZ A, WERNER L. Separation of nanoparticles from air using melt-blown filtering media[J]. Aerosol and Air Quality Research, 2015, 15(6): 2422-2435.

[3] BOLBASOV E N, STANKEVICH K S, SUDAREV E A. The investigation of the production method influence on the structure and properties of the ferroelectric nonwoven materials based on vinylidene fluoride- tetrafluoroethylene copolymer[J]. Materials Chemically and Physics, 2016,182: 338-346.

[4] JULIEN P, PHILIPPE V, MARYLINE L, et al. Influence of fiber diameter, fiber combinations and solid volume fraction on air filtration properties in non-wovens[J]. Textile Research Journal, 2012, 82(19): 1948-1959.

[5] AMIT R. Structural analysis of pore size distribution of nonwovens[J]. The Journal of the Textile Institute, 2010, 101(4): 350-359.

[6] WANG Z H, SHU L, DING X Y. Minimal description and maximal description in covering-based rough sets[J]. Fundamental Information, 2013, 128(4): 503-526.

[7] SUN B Z, MA W M, ZHAO H Y. Rough set-based conflict analysis model and method over two universes[J]. Information Sciences, 2016,372: 111-125.

[8] 刘贵, 于伟东. 基于粗糙集的精毛纺粗纱工艺规则推理和案例组织[J]. 纺织学报, 2008, 29(12): 17-21.

LIU Gui, YU Weidong. Worsted roving process′s rule extraction and cases based on rough set[J]. Journal of Textile Research, 2008, 29(12): 17-21.

[9] ZHANG C H, SHAO Y H, TAN J Y, et al. Mixed-norm linear support vector machine[J]. Neural Computing & Applications, 2013,23:2159-2166.

[10] RAWAL A, MAJUMDAR A, ANAND S, et al. Predicting the properties of needle punched nonwovens using artificial neural network[J]. Journal of Applied Polymer Science, 2009, 112: 3575-3581.

[11] 陈鸿烈, 蔡大伟, 胡慧兰. 不同模式时距对模式预测能力影响之研究[J]. 水土保持学报, 2006, 38(2): 141-156.

CHEN Paris Honglay, TSAI David D W, HU Huilan. Influence of modal time periods on modal predictive ability[J]. Journal of Soil and Water Conservation, 2006, 38(2): 141-156.

[12] 鞠金艳, 王金峰. 基于BP神经网络的农业机械化作业水平预测[J]. 农机化研究, 2015(3): 74-78.

JU Jinyan, WANG Jinfeng. Prediction the operation level of agricultural mechanization based on BP neural network[J]. Journal of Agricultural Mechanization Research, 2015(3): 74-78.

[13] DEDOV A V. Estimation of the air permeability of needle punch materials[J]. Fiber Chemistry, 2007, 39(6): 454-456.

[14] JANKOWSKI T. Influence of structural characteristics on liquid aerosol filtration in multilayer nonwoven fabrics of the spunlace type[J]. Fibers & Textiles in Eastern Europe, 2009, 17(4): 87-92.

[15] 高晓艳, 张露, 潘志娟. 静电纺聚酰胺6纤维复合材料的孔隙特征及其过滤性能[J]. 纺织学报, 2010, 31(1): 5-10.

GAO Xiaoyan, ZHANG Lu, PAN Zhijuan. Porous characteristics and filtration properties of electrospun PA6 fiber composite[J]. Journal of Textile Research,2010, 31(1): 5-10.

[16] 武松梅, 袁传刚. 非织造材料孔径与过滤性能关系的研究[J]. 产业用纺织品, 2010(1): 12-14.

WU Songmei, YUAN Chuangang. Study on relation between pore size of nonwovens and filtration characteristic[J]. Technical Textiles, 2010(1): 12-14.

[17] DOLNY S, ROGOZINSKI T. Air flow resistance across nonwoven filter fabric covered with microfiber layer used in wood dust separation[J]. Drewno, 2014, 57(191): 125-134.

[18] 简小平. 非织造布空气过滤材料过滤性能的研究[D]. 上海: 东华大学, 2013: 40-46.

JIAN Xiaoping. A study on filtration performance of nonwoven air filtering material[D]. Shanghai: Donghua University, 2013:40-46.

[19] SIMMONDS G E, BOMBERGER J D, BRYNER M A. Designing nonwovens to meet pore size speci-fications[J]. Journal of Engineering Fibers and Fabrics, 2007, 2(1):1-15.

[20] 潘莺, 王善元. 模拟熔喷纤网的孔径分布及其对过滤性能的影响[J].中国纺织大学学报, 2000, 26(5): 73-77.

PAN Ying, WANG Shanyuan. Simulation of melt blown web and the effect of its pore size distribution on filtration performance[J]. Journal of China Textile University, 2000, 26(5): 73-77.