金属材料在冲击荷载下局部变形的数值模拟及分析
陈小翠, 杜成斌, 江守燕(河海大学 力学与材料学院, 南京 211106)
当金属材料受高应变率载荷作用时,如爆炸、子弹射击、高速撞击、切削等,会产生集中于很窄的带状区域内的严重塑性变形,通常叫做绝热剪切带[1]。剪切带宽度一般为10 μm量级,而且传播的速度很快,为微秒量级[2-3]。金属扭转、拉伸实验中经常观察到带内产生剧烈的塑性变形,且带内温度高达100 °C量级。这些因素对材料造成不可逆损伤,如孔洞和断裂的生长[4-5],甚至造成材料的断裂破坏[6]。
高应变率作用下,塑性变形通常使用与应变率、应力和温度相关的本构方程来描述,塑性变形产生的热能具有软化效应,促使塑性流动产生,而应变率和应力的增加则产生材料硬化效应。Marchand和Duffy的实验指出[7],剪切变形局部化形成过程主要分为3个阶段:第一阶段主要是局部化发生之前,材料从弹性阶段发展到均匀塑性变形阶段;第二阶段材料温度快速增长,塑性变形增大,应力应变曲线出现应力峰值,材料开始应变软化;第三阶段即材料失稳阶段,材料应力极限下降,产生严重的材料局部化,导致金属材料承载能力下降。
剪切带现象不仅是多物理场的热力耦合问题,更具有微米级的空间尺寸和微秒级的时间尺度,准确模拟剪切带的产生和生长一直是研究的难题[8]。考虑到问题的复杂性,在模拟过程中人们一般采用绝热剪切的假设来简化模拟过程中的数值计算难度[9-11]。但该假设忽略了热扩散效应,即不考虑局部化形成过程中热传导与热能之间的相互作用,这样通常伴随着网格敏感性[12]。
白以龙等[13-14]提出了热塑剪切带问题,强调耦合热传导和塑性功效应的重要性,并基于假设计算出一维热塑剪切带问题的准定常近似解,将剪切带宽度的形成看作是塑性功和热扩散相互平衡的产物。
本文基于有限元分析软件FEAP (Finite Element Analysis Program)[15],用Fortran语言编写一个新的单元。该单元在能量方程中考虑了热扩散作用,基于混合有限元的理论框架,同时将位移、温度、应力和等效塑性应变场作为未知量,同步进行求解适用于高应变率作用下塑性变形局部化问题的偏微分方程组,适用于模拟二维塑性变形局部化问题。文中基于该单元进行了经典的45°剪切带问题模拟,并将计算结果与绝热假设结果比较,观查网格敏感性。文中同时考虑了使用显式算法和隐式算法进行剪切带数值模拟,并将两者的计算精度及计算成本进行对比。
1 控制方程
冲击荷载作用下的剪切带问题的模拟用偏微分方程组(PDEs)来表示,主要为动量守恒方程、能量守恒方程、弹性本构和塑性本构关系。
不考虑体力作用,动量守恒方程表示为

(1)
式中:u为位移向量,σ为应力张量,ρ为材料密度。

(2)
式中:T为温度场,κ和cp分别为热导率和比热容,Dp为塑性变形率。
基于小变形假设
(3)

(4)
式中:v为速度向量;L为速度梯度张量。
根据弹塑性力学理论,考虑温度效应的热变形,则在弹塑性状态下本构方程中变形率由三部分组成:弹性应变率Del、 温度变化引起的应变率DT和非弹性应变率Dp,即
D=Del+DT+Dp
(5)
根据胡克定律(Hooke’s Law),弹性本构方程为
(6)

剪切带形成过程中伴随着应变硬化、应变率硬化及热软化等作用,假设屈服应力与应力、温度及塑性变形相关,本文采用修正Litonski[16-17]塑性本构方程
(7)
(8)
(9)
上式表明塑性应变张量与偏应力张量方向相同。
由于
(10)
(11)
式中:“:”指张量的双点积运算。
根据式(10)和式(11),控制方程简化为

(12)
边界条件为
(13)

2 离散模型
PDEs的弱形式通过将各个方程乘以各自的试探函数:ωu,ωT,ωσ和ωγp,并在求解域Ω上进行积分。再根据分部积分原理,对偏微分方程降阶。则R表示为
(14)
(15)

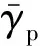
(16)
3 时间离散模型

3.1 隐式算法
文中在建立本构方程时采用率形式,因此在计算过程中可直接采用速度场v来代替位移场u作为变量,在时间离散过程中只需要变量的一阶导数项,相对于隐式积分,可采用后向欧拉迭代法(Backward Euler Method)。
若对变量α采用隐式时间离散方法,则变量α和β均采用隐式算法。对于隐式算法,在每一个时间增量步都需要对非线性方程进行线性化并迭代求解。
R表示为在xn附近的Taylor展开式,仅保留线性项,在xn增量方向通过Gateaux求导,得出Jacobian矩阵,如下式所示
(17)
式中:J为雅可比矩阵;θ为无穷小量。故离散后方程可以表示为
(18)
式中:
(19)
(20)

(21)
(22)
因此式(18)可简化为
(23)
回顾上节的Schur补方法,上式简化为
(24)
用数学方法展开
(25)

3.2 半显式算法
倘若对变量α采用前向欧拉方法(Forward Euler Method),即显式时间离散方法,而变量β采用隐式算法,则该模型采用半显式算法离散。对于变量α计算过程如下
(26)
一直以来,显式算法经常被用于求解需要分许多时间增量步的高速动力学问题,如冲击、碰撞、爆破之类高度非线性问题。但显式算法时间步长的选择直接关系到数值模拟的稳定性及计算时间。对于剪切带模拟过程中时间增量的选择,文中假设材料变形一直处于弹性阶段,则变量α表示的动量守恒方程和能量守恒方程需要满足不同的时间步要求,分别为力学问题和热问题所需要满足的时间步条件。
对于力学问题,临界时间步为膨胀波传播过程中通过最小网格单元所需的时间[20],表示如下
(27)
式中:h为单元尺寸;c为P波速;λ和μ为Lame常数。
对于热效应问题,临界时间步为热波通过最小网格单元所需的时间,表达如下
Δtth=min(ρcph2/2κ)
(28)
因此,对于上述模型,临界时间步长为
Δt=γmin(Δtth,Δtmech)
(29)
式中:γ为考虑非线性问题的折减系数。
4 数值算例
4.1 算例1
本算例考虑上下两端竖向受拉的金属材料方板。板的具体受力状态及速度边界条件,如图1所示。方板中心设有一个圆形缺陷,来诱发剪切带的产生(图1中圆形区域内为缺陷)。模型及其受力状态关于x轴与y轴对称,取右上角1/4方板进行模拟,在1/4方板左侧及底部施加对称边界约束。
缺陷内屈服应力和屈服应变值由二维β函数折减
(30)
式中:α为折减系数;(x0,y0)缺陷中心坐标;r0为折减半径。本算例中取α=4%,x0=0,y0=0,r0=1 μm,即半径为1 μm范围内材料屈服应力和屈服应变均折减4%,来诱发剪切带的产生。
数值计算时,假设平面应变状态,板的宽度为100 μm,即H=50 μm。施加的速度边界条件,如图2所示。1 μs内速度从0线性增长到5 m/s,随后保持不变,即vr=5 m/s,tr=1 μs。本算例采用的材料参数及材料相应的塑性本构模型的参数详见表1。

图1 方形板结构及边界条件(虚线区域为缺陷位置)Fig.1 Square plate configuration and boundary conditions

图2 速度边界条件Fig.2 Velocity profile used as a loading function

表1 算例1采用材料参数Tab.1 Material parameters used in the first example
为显示热传导效应在该模拟过程中的重要性及其对网格依赖性的缓解作用,本文分别进行了绝热假设模拟(κ=0)和热扩散模拟,将四分之一板离散成50×50,80×80和100×100的均匀网格,使用隐式时间算法。计算总时长2.0 μs,时间步长取5 ns。绝热假设和热扩散模拟的数值分析结果,如图3所示。其中包括应力随时间变化曲线,t=2 μs时方形板主对角线方向(图1虚线处)的等效塑性应变(EQPS) 分布图。
从图1可知,考虑热传导效应模拟剪切带,应力时程曲线及剪切带宽度、等效塑性应变峰值的结果都比较稳定,对网格依赖性小。反之,绝热假设导致应力时程曲线的应力软化阶段出现明显的网格依赖性。剪切带内的塑性变形被放大,过高地估计了剪切带内的塑性应变及温度。
图4表示出模拟终止时100×100网格模型热扩散项与塑性功产生的热源项沿对角线的分布图。图5为相同工况下的等效塑性应变云图。从图5可知,剪切局部化范围内热扩散项与热能同一量级,符号相反。与文献[13-14]结论一致,在能量方程中引入热传导使得热能与热扩散互相对抗,形成模型内部尺寸效应,从而减弱网格依赖性。因此,不管从物理角度还是从数学角度,在能量守恒中考虑热耗散项均具有重要意义。
4.2 算例2
本算例采用“4.1”节的模型,材料参数及网格尺寸均与算例1相同,但此算例进行半显式离散模拟及隐式算法模拟的计算结果、计算成本等比较。基于算例1,在隐式和显式模拟过程中均考虑热扩散效应。

(a) 应力时程曲线

(b) 方形板对角线方向的EQPS分布曲线(t =2 μs)图3 绝热假设与热耗散模拟结果比较Fig.3 Comparison of adiabatic and diffusion assumptions with different meshes

图4 对角线处热耗散项与热源项分布曲线(100×100网格,t=2 μs)Fig.4 Source and diffusive term along the diagonal of the plate plotted at the final time
采用50×50,80×80和100×100的均匀网格, 对应的网格尺寸分别为h=1 μm、h=0.625 μm和h=0.5 μm。依据式(28)和式(29)及不同网格尺寸,显式模拟的极限时间步长分别为Δtcr=3.48 ns,Δtcr=1.36 ns和Δtcr=0.87 ns。考虑非线性问题,最终显式时间步长分别取为Δt=0.04 ns,Δt=0.02 ns和Δt=0.02 ns。隐式模拟的时间步长均取为Δt=10 ns。计算总时长为2 μs。施加的速度边界条件与算例1相同,即vr=5 m/s,tr=1 μs。为了区分冲击荷载对计算结果的影响,对于100×100的网格还分别进行了vr=10 m/s的两种不同时间离散的数值模拟。

图5 EQPS云图(100×100网格,t=2 μs)Fig.5 EQPS field at the final time
图6为两种离散方法模拟的材料应力随时间变化的曲线。从图中可以看出两种方法的应力曲线吻合很好,且网格的尺寸敏感性小。图7针对100×100网格,比较了不同时间迭代方法及不同冲击速度条件下得到的等效塑性应变及温度场沿主对角线的分布情况。显式与隐式模拟均在Dell optiplex 755电脑上进行,4 GB内存,4核2.83 GHz。结果表明对于45°剪切带问题,增大冲击速度明显增大了剪切带内的等效塑性应变及带内温度,使剪切带内的塑性变形更剧烈,但是不同速度边界条件下,针对所选的时间步长,两种算法的计算精度都基本一致。考虑显式算法的条件稳定性,时间步长需要比隐式算法小很多。不同网格的总模拟cpu时长及隐式算法的单位时间步的平均迭代次数Niter列于表2中(vr=5 m/s)。虽然显式算法的计算精度与隐式算法相同,但显式算法的cpu时长远远大于隐式算法的时长(见表2)。

图6 绝热假设与热耗散模拟结果比较Fig.6 Comparison of adiabatic and diffusion assumptions with different meshes

(a) 对角线方向EQPS分布曲线

(b) 对角线方向温度分布曲线图7 不同速度边界条件下100×100网格显式算法与隐式算法结果比较
Fig.7 Results obtained with explicit and implicit scheme plotted at the final time with the finest mesh under different velocity impact

表2 不同算法的Cpu时长比较(vr=5 m/s)Tab.2 Cpu time comparison (vr=5 m/s)
因此,尽管显式算法经常被广泛用于求解高速动力学问题,但对于冲击荷载下45°剪切带问题,为了满足计算的精度要求,需要采用很小的时间步长,导致计算所需成本比隐式算法大很多。本文编写的单元采用隐式算法迭代收敛稳定,计算精度高,且因为考虑了热传导作用,网格敏感性小。
5 结 论
本文研究了在高速冲击荷载作用下金属材料局部剪切带形成过程的模拟方法,并使用Schur补方法节约计算成本。在混合有限元的基础上,基于有限元分析程序FEAP (Finite Element Analysis Program),使用Fortran语言编写一个新单元,该单元将位移、温度、应力和等效塑性应变场统一作为未知量,同步进行求解适用于高应变率作用下塑性变形局部化问题的偏微分方程组,Jacobian矩阵通过对残余向量在未知量增量方向进行Gateaux求导计算出理论解,避免数值微分的过程及误差。针对该计算模型,
(1) 模拟过程中在能量方程中同时考虑了热传导效应及塑性功产生的热能作用,在非线性问题的模型内部引入尺寸效应,有效地限制剪切局部化变形范围,缓解了剪切带模拟的网格敏感性现象。
(2) 该模型在空间上Galerkin离散,在时间上分别进行了半显式算法(应力及塑性应变变量采用隐式时间离散,而位移和温度变量为显式迭代)与隐式算法的剪切带模拟。
(3) 依据显式算法与隐式算法模拟结果对比得出,对于剪切带问题的模拟,显式算法的精度并不及隐式算法,为了使显式算法的计算精度满足要求,需要选取很小的时间步长其计算成本比隐式算法大很多,而文中的模型采用隐式算法迭代,迭代收敛稳定,不仅时间成本低,而且计算精度高。
致谢本论文得到国家留学基金委资助(201506710022),感谢美国哥伦比亚大学土木工程与工程力学系Haim Waisman教授及其课题组的指导与帮助。
参 考 文 献
[1] 徐永波,白以龙.动态载荷下剪切变形局部化、微结构演化与剪切断裂研究进展.力学进展,2007,37 (4):496-516.
XU Yongbo, BAI Yilong. Shear localization, microstructure evolution and fracture under high-strain rate[J]. Advances in Mechanics,2007,37(4): 496-516.
[2] WRIGHT T W, BATRA R C. The initiation and growth of adiabatic shear bands[J]. International Journal of Plasticity, 1985,1(3): 205-212.
[3] DODD B, BAI Y. Adiabatic shear localization[M]. 2nd ed. Oxford: Elsevier, 2012.
[4] OSOVSKI S, RITTEL D, LANDAU P, et al. Microstructural effects on adiabatic shear band formation[J]. Scripta Materialia, 2012, 66(1): 9-12.
[5] OSOVSKI S, RITTEL D, VENKERT A. The respective influence of microstructural and thermal softening on adiabatic shear localization[J]. Mechanics of Materials, 2013, 56:11-22.
[6] WRIGHT T W. The physics and mathematics of adiabatic shear bands[M]. Cambridge: Cambridge University Press, 2002.
[7] MARCHAND A, DUFFY J. An experimental study of the formation process of adiabatic shear bands in a structural steel[J]. Journal of the Mechanics and Physics of Solids,1988, 36(3): 251-283.
[8] JOHNSON G R, COOK W H. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]∥Proceedings of the 7th International Symposium on Ballistics. Hague, Netherlands,1983.
[9] LI S, LIU W K, ROSAKIS A J, et al. Mesh free galerkin simulations of dynamic shear band propagation and failure mode transition[J]. International Journal of Solids and Structures, 2002, 39(5): 1213-1240.
[10] BELYTSCHKO T, CHIANG H Y, PLASKACZ E. High resolution two dimensional shear band computations: imperfections and mesh dependence[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 119(1): 1-15.
[11] 王猛,杨明川,罗荣梅,等. 钨合金杆式弹穿甲侵彻开坑阶段绝热剪切失效的数值模拟[J].振动与冲击, 2016, 35(18): 111-116.
WANG Meng, YANG Mingchuan, LUO Rongmei, et al. Numerical simulation on the adiabatic shear failure at cratering stage for tungsten alloy long rod penetrator piercing into armor[J]. Journal of Vibration and Shock, 2016, 35(18): 111-116.
[12] NEEDLEMAN A. Material rate dependence and mesh sensitivity in localization problems[J]. Computer Methods in Applied Mechanics and Engineering, 1988, 67(1): 69-85.
[13] 白以龙,郑哲敏,俞善炳. 关于热塑剪切带的演变[J].力学学报,1986, 18(增刊2): 377-383.
BAI Yilong, ZHENG Zhemin, YU Shanbing. On evolution of thermo-plastic shear band[J]. Chinese Journal of Theoretical and Applied Mechani, 1986, 18(Sup2): 377-383.
[14] 白以龙,郑哲敏,俞善炳. 热塑剪切带后期演变的准定常近似[J].固体力学学报, 1987(2):153-158.
BAI Yilong, ZHENG Zhemin, YU Shanbing. Quasi steady approximation to the late stage evolution of thermo-plastic shear band[J]. Chinese Journal of Solid Mechanics, 1987(2): 153-158.
[15] TAYLOR R L. FEAP—A finite element analysis program[D]. Berkeley, CA:University of California, 2011.
[16] ZHOU M, RAVICHANDRAN G, ROSAKIS A J. Dynamically propagating shear bands in impact-loaded pre-notched plates—II. numerical simulations[J]. Journal of the Mechanics and Physics of Solids, 1996, 44(6): 1007-1032.
[17] MCAULIFFE C, WAISMAN H. A pian-sumihara type element for modeling shear bands at finite deformation[J]. Computational Mechanics, 2013, 53(5): 925-940.
[18] SCHUR J. Über potenzreihen, die im innern des einheitskreises beschraänkt sind[J]. Journal für die Reine und Angewandte Mathematik, 1917, 147:205-232.
[19] BERGER-VERGIAT L, MCAULIFFE C, WAISMAN L. Isogeometric analysis of shear bands[J]. Computational Mechanics, 2014, 54(2): 503-521.
[20] HUGHES T J R. The finite element method: linear static and dynamic finite element analysis[M]. 2nd ed. Mineola, NY: Dover Publications, 2000.

