西安市公交协同调度优化研究

李嘉鸣

（长安大学 汽车学院，陕西 西安 710064）

前言

目前，在公交的运营管理方面，西安市以单线运营调度为主，即定线、定人、定站、定时的调度方式。单线调度时，线网中各条线路的运营计划相互独立，线路之间协同性差，造成公交公司的运营效率低，乘客候车时间长[1]。

为了解决上述问题，本文尝试将线网协同调度的概念应用于西安市公交调度的优化过程中。即将传统的以疏散某条线路在高峰时段的最大客流量为目标编制单线调度时刻表，改为编制以实现乘客在线网中总的换乘时间最短为目标的公交线网协同调度时刻表。

1 公交换乘客流调研

1.1 调研内容

由于人力有限，本文选择西安市36路、103路公交部分路段作为研究对象展开调研，并将运行时间指标进行简化，以车辆从始发站到换乘站总的运行时间为研究对象[2]。调研内容如下表1，表2所示：

表1 线路基本情况

表2 线路运行情况

1.2 调研时间

为充分体现不同交通流量对换乘客流量模型的影响，调研时段应包含高峰时段和平峰时段，故将调研时段定为下午5至7时。为了使调研数据具有较高的一致性，将调研日期统一为工作日，共三天。

1.3 调研方法

由于西安市公交为上车刷卡购票，没有配备乘客自动计数系统，所以采用人工调研。其中，线路基本情况和发车间隔时间Hk通过询问调度人员和互联网搜索来获得，线路运行情况采用驻站调查法。

2 调度时刻表优化模型

2.1 运行时间模型和换乘客流量模型

为了计算方便，将下午5时规定为0时刻，对相关时刻进行改写。将得到的数据利用Matlab软件的smooth函数进行平滑处理，然后取整。

计算每一班次车辆在其路段的运行时间：

式中：Dik：线路k上第i班公交在起点站的发车时刻；

Hk：线路k的发车间隔；

Tikn：线路k上第i班公交从起点站到换乘站点n的运行时间；

Aikn：线路k上第i班公交到达换乘站点n的时刻。

最后，为了数据的一致性和代表性。将三天的数据对应相加后取平均值并取整，得到最终用来建立模型的数据。

利用Matlab软件的曲线拟合工具箱，通过比较不同拟合类型下，和方差和确定系数这两个评价指标值的大小，得到运行时间模型和换乘客流量模型。

2.2 线网协同调度模型

2.2.1 模型假设

作如下假设，以便对研究问题进行简化[4]：

（1）研究周期为120min；

（2）运行时间服从运行时间模型，换乘客流服从换客流量模型；

（3）每发一趟车的运营成本为80元。

2.2.2 参数定义

（1）线网符号

M：公交线路总条数；

N：换乘站点总个数；

k，q：公交线路标记；

n：换乘站点标记。

（2）决策变量

Sk、Sq：线路k，q上首班车发车时刻的调整值。

（3）状态变量

Fk、Fq：线路k，q理论发车次数；

Qkqn、Qqkn：在换乘站点n处线路k和q之间换乘的乘客数；

Djq：线路q上第j班公交在起点站的发车时刻，表示为：

Hq：线路q的发车间隔；

Tjqn：线路q上第j班公交从起点站到换乘站点n的运行时间；

TRqkn：换乘站n处，乘客从线路q到线路k的换乘时间；

TRkqn：换乘点n处，乘客从线路k到线路q的换乘时间；

Hmink、Hmaxk：线路k发车间隔的上下限；

Hminq、Hmaxq：线路q发车间隔的上下限；

A1：每名乘客每分钟的折算损失；

A2：每发一趟车的折算运营成本。

2.2.3 模型建立

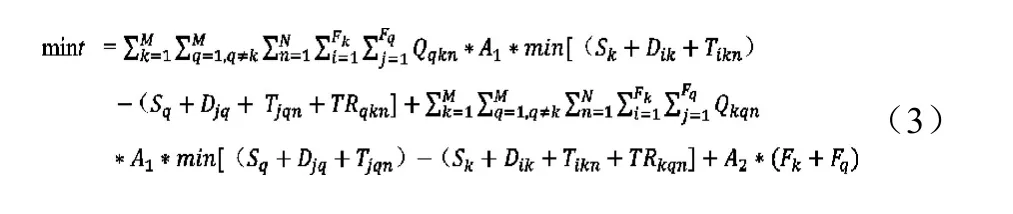
约束条件：

2.3 改进的遗传算法

由于遗传算法的并行化处理功能和较高的寻优效率的优点，本文根据线网协同调度的特点，设计改进的遗传算法对模型进行求解。

改进算法流程图：

图1 问题的优化流程图

2.3.1 初始化种群

根据线网协同调度问题的特点，采用 crtbp函数创建任意离散的随机种群。

2.3.2 优化算法

（1）染色体编码：

将模型中的变量Sk、Sq转换成二进制字符串，要求的精度是保留到整数位。

（2）初始种群：

令NIDN=100，即初始种群具有100个体，由电脑随机产生。

（3）适应度函数：

由于本文是求解最小值问题，所以将目标函数作为适应度函数。使用Matlab中ranking函数进行适应度值的分配。另外，将约束条件作为惩罚函数进行处理。

（4）算子：

选择：使用select函数实现随机遍历采样。

交叉：本文采用xovsp函数来进行个体之间的单点交叉，交叉概率取0.7，交叉后使用recombin函数进行重组，得到新的个体。

变异：本文的决策变量为整数，变异概率取0.01，采用函数mut实现变异操作。

种群选取：采用 ranking函数实现个体目标值由小到大的排序，并返回一个包含个体适应度值的列向量。

（5）终止条件：

本文将最大遗传代数作为终止条件，当遗传代数达到500次时终止进化。

3 实例分析

表3 线路基本情况

利用调研数据来验证前面章节中模型及算法的可行性与有效性。

调研得到的线路基本情况如表3。

根据调研的线路运行情况，得到研究时段内的运行时间模型和换乘客流量模型。

以字母k表示103路，q表示36路。将Hk、Hq依次取值 2min，3min，4min，5min，6min，计算不同Hk、Hq对应的发车次数Fk、Fq。

式中：G：2016年人均GDP。

经计算 A1=0.53元/分钟；A1，A2为整数，所以将 A1，A2同乘以100进行替换，这么做不影响目标函数意义的表达。

将它们带入线网协同调度模型中，运用遗传算法计算出Sk、Sq以及目标函数的最小值。经过比较分析，当Sk=1，Sq=0，且当Hk=2min，Hq=2min时，目标函数最小。

进而得到优化后的线网协同发车时刻表如下：

表4 优化后的发车时刻表

4 结论

本文通过对西安市36路和103路两条线路进行调研，利用回归分析得到两条线路的运行时间模型和换乘客流量模型，进而建立了公交线网协同调度模型。而后进行了实证分析，利用优化的遗传算法对调度模型进行求解，得到不同发车间隔下各线路首班车发车时刻的调整值和目标函数值，进行分析比较得到优化后的协同调度时刻表。

[1] 苏彩艳.基于运行时间可靠性的公交线网协同调度问题研究[D].湖南:中南大学,2012.

[2] 颜建新.基于换乘的公交区域调度与乘客出行路径优化方法[D].南京:东南大学2010.

[3] 李臻.城市公交车辆智能调度优化研究[D].山东:山东科技大学,2010.

[4] 戴帅,陆化普,胡启洲.基于一体化的多层次公交线网优化研究[J].数学的实践与认识,2011, 41(1):85-93.

[5] 覃运梅.城市公交调度优化方法研究[D].安徽:合肥工业大学,2006.