基于动态时间弯曲的轨道波形匹配方法

朱洪涛， 李 姗， 肖 勇， 魏 晖(南昌大学 机电工程学院，南昌 330031)

轨道平直度测量仪(简称平直尺)利用激光测距原理，可实时将所测轨道波形以数据的形式反映出来。目前市场上生产的平直尺，在实际工程上主要有两方面的应用：一方面是为了测量钢轨的焊缝，以此来评价钢轨焊缝的焊接质量[1]；另一方面是为了分析轨道表面的短波不平顺，对某段钢轨的波形进行处理和分析[2]。由于测量采用静态测量方法[3]，并且因测量装置的限制，仅通过平直尺的单次测量难以满足测量要求，故需要进行多次测量，再利用匹配技术对数据进行整合和分析，来客观显示轨道上的短波变化规律。

目前在轨道短波的匹配研究中，Kong等[4]采用动态规划(DP)算法，对二维曲线进行匹配，但未考虑曲线不完全匹配的情况；Ucoluk等[5]研究了曲线的自动匹配问题，但在局部匹配中采用了穷举法，这使匹配复杂度较高而匹配效率低下，并且没有运用到实际测量中进行测试，缺乏说服力；余先川等[6]提出基于区域的匹配，该方法一般通过求解曲线相关系数来实现，但计算量大，运行时间较长；牛小兵等[7]提出了基于特征的匹配方法，可以提取有缩放、平移和旋转不变性的特征点，具有快速、准确的特点，但如果特征点的提取不好，则会产生较大的误差，严重影响匹配效果。以上这些传统匹配算法只能对坐标系内的曲线进行刚性的变换和匹配，无法解决不同坐标系下曲线的动态匹配问题。

本文利用二维坐标转换公式，将待匹配曲线经旋转和平移后，统一到同一坐标系下。基于此，提出了一种基于动态时间弯曲(DTW)的轨道短波匹配方法，通过对横坐标时间轴的弯曲和变形，发现相似波形并构造累积代价矩阵；利用递归思想，可计算两条曲线的最短弯曲路径，并求出两条待匹配曲线之间的单点对应关系，以此来进行精准的点对点匹配，从而实现了轨道短波的精准动态匹配。

1 系统的构成及测量原理

1.1 系统的构成

测量系统主要由激光位移传感器、编码器、接近开关、步进电机、步进电机驱动器、STC单片机及上位机组成，测量系统的结构图如图1所示。

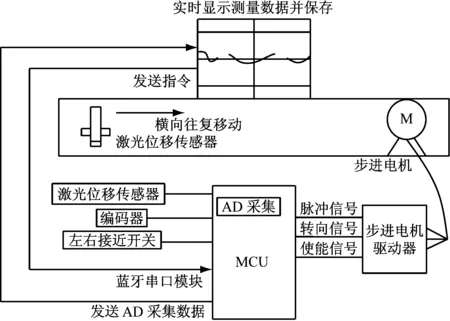
图1 测量系统结构图Fig.1 Structure diagram of measuring system

1.2 系统测量原理

设定激光传感器在导轨上运动一次时，所采集的数据点为N个。将第一点的测量值y0作为参考点，激光器向后测量的N-1个点y1至yN-1中，利用第一点的测量值y0依次减去其他被测点yi(i=1,2,…,N-1)，则可求出两点之间的相对距离y，即

y=y0-yi(i=1,2,…,N-1)

(1)

通过获取传感器探头与被测轨面之间的距离，可以间接表示出所测钢轨的表面形状曲线。测量原理图如图2所示。

2 匹配前的坐标转换

在实际测量过程中，由于受轨道原始形状的影响，每次测量的数据是在不同坐标系下完成的，如图3所示。所以，为了进一步对数据进行匹配，首先需要将数据进行坐标系的转换，将所测数据统一在同一坐标系下。

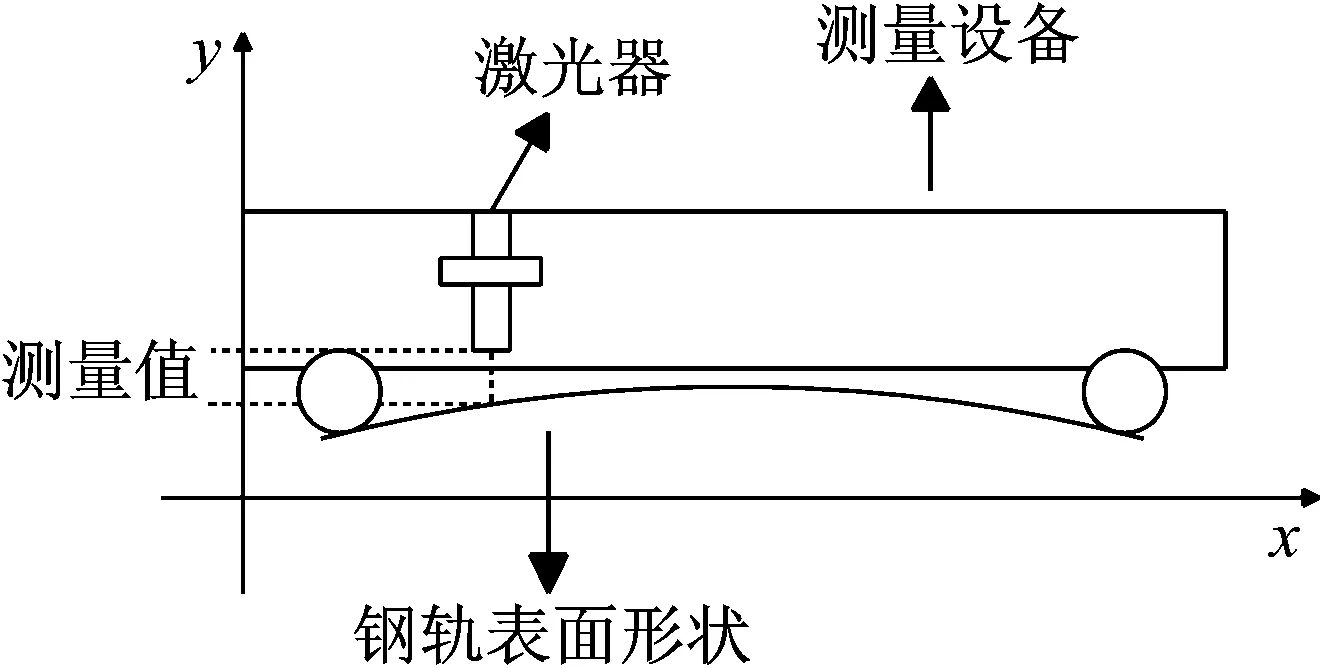
图2 测量系统原理图(mm)Fig.2 Schematic diagram of measuring system(mm)

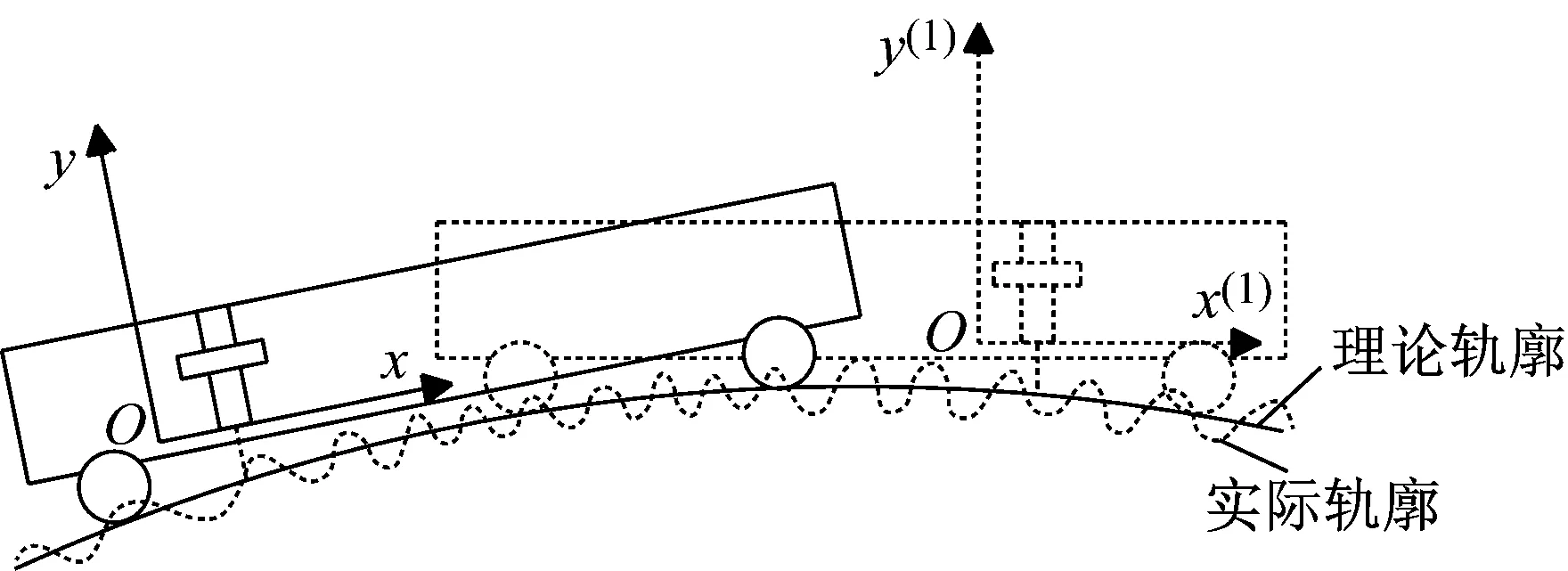
图3 实际测量坐标图Fig.3 Practical measurement coordinate diagram

设{o;x,y}和{o;x(1),y(1)}为测量平面的两组坐标系，横坐标表示测量里程，纵坐标为轨道短波不平顺值。对于轨道表面的同一测量点a，在不同位置下的测量值因坐标系的不同而不同。如图4所示，坐标系{o;x(1),y(1)}相对于坐标系{o;x,y}平移了(x0,y0)，且逆时针旋转了角度θ，使得测量点a在{o;x,y}和{o;x(1),y(1)}两坐标系下的测量值分别为(x,y)和(x1,y1)，为了将测量重复段内的数据进行匹配，须对坐标系进行统一和转换。

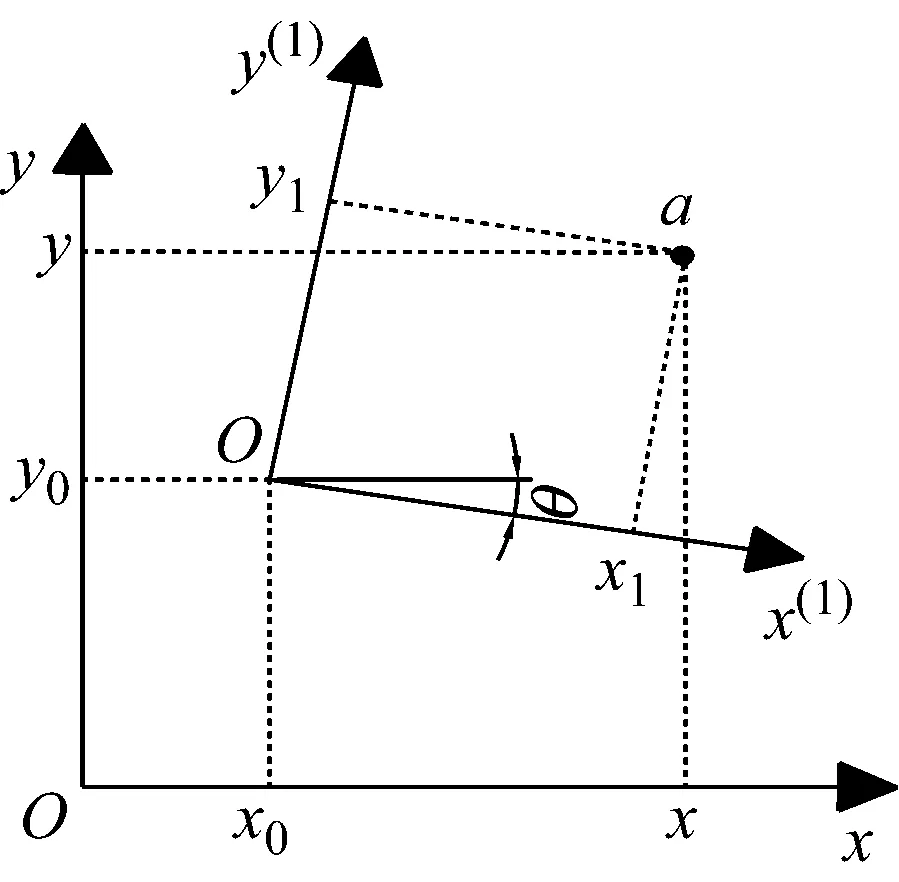
图4 不同坐标系下的数值显示Fig.4 Numerical display in different coordinates

坐标转换公式为

x=x1cosθ-y1sinθ+x0

y=x1sinθ+y1cosθ+y0

(2)

将式(2)转化为矩阵表达式为

(3)

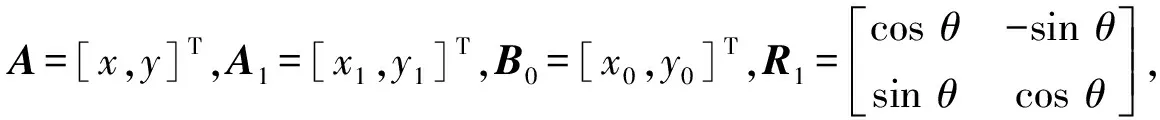
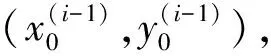
Ai-1=RiAi+Bi-1(i=1,2,…,n)

(4)

根据迭代思想，将其他i个坐标系转换到第一个坐标系{o;x,y}的转换表达式为

(5)

3 基于动态时间弯曲的波形匹配算法

动态时间弯曲(Dynamic Time Warping,DTW)算法由于具有很好的鲁棒性，较高的匹配精度，通常应用在语音识别等模式识别领域[8-9]。该算法通过对横坐标时间轴的扭曲和变换，发现相似波形，使其特征与参考模板进行匹配[10]。由于实际测量过程中，每次测量方向和角度的变化以及人为或环境影响的偶然误差存在，使所测重合部分的数据不会完全相同，测量曲线在匹配过程中会有一定的变形和偏差。故在匹配过程中，需要对待匹配曲线的横坐标进行弯曲变形后，才能进行高精度的动态匹配。引入DTW算法，从而实现了轨道波形的精准点对点匹配。

3.1 动态时间弯曲算法原理

由测量原理可知，数据采集中的横坐标是每隔5 mm测一个点，等距测量可以等效为等时间间隔测量，故可将横轴的里程等价为时间来衡量。假设在第i个坐标系{o;x(i),y(i)}内的N个测量数据存放在时间序列P，在第i-1个坐标系{o;x(i-1),y(i-1)}内的M个数据存放在时间序列Q，那么

P=[p1,p2,p3,…,pn,…,pN]

Q=[q1,q2,q3,…,qm,…,qM]

定义距离函数：dij=f(pi,qj)。

其中f表示实际采用的测距函数，最常用的是二阶距离[11]，即：

(6)

由式(6)可知，根据时间序列P、Q内不同数据对象之间点与点的欧氏距离，构成了N×M的动态时间扭曲距离矩阵d

在矩阵d中，相邻矩阵元素的集合构成了一条弯曲路径，记为W={w1,w2,…，wk}，其中W中的第k个元素wk=(dij)k。弯曲路径需满足以下条件[12-13]

(1)有界性：w1=d11，wk=dMN；

(2)连续性：若wk=(pa,qb)，wk-1=(pa′,qb′)，则有0≤|a-a′|≤1,0≤|b-b′|≤1;

(3)单调性：若wk=(pa,qb)，wk-1=(pa′,qb′)，则有a≥a′,b≥b′;

(4)边界条件：弯曲路径中的总元素数k需满足max(M,N)≤k≤M+N-1；

由弯曲路径的必要条件可知，满足上述条件的弯曲路径不止一条，根据穷举法，可以将所有的弯曲路径一一列出。但时间序列P和Q的DTW距离指两时间序列间的最短弯曲路径Wbest[14]

(7)

其中K为消除时间序列长度不一的影响因子。

为求解式(7)，由递归思想，构造累积代价矩阵γ，即

(8)

式(8)中，i=1，2，…，N；j=1,2,……，M，γ(0,0)=0，γ(i,0)=γ(0，j)=+∞故时间序列P和Q的DTW距离为

DTW(P，Q)=γ(N，M)

(9)

3.2 数据匹配算法的实现

由平直尺的测量原理可知，前后两次测量数据的时间序列P和Q中有一半数据是重复测量所得。若要将相似的时间序列Pi和Qj匹配，首先通过求解弯曲路径曲线W的距离，找到经过时间轴的弯曲和变形后两个时间序列之间的最短弯曲路径Wbest(即DTW距离)，并在此过程中确定两时间序列各点的最佳对应关系。如图5所示。

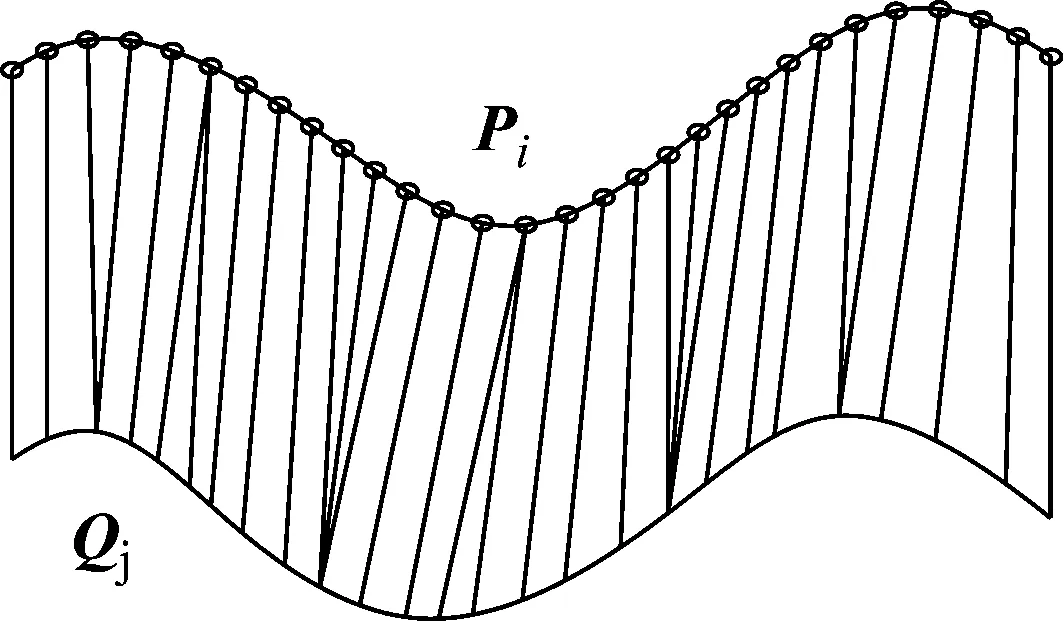
图5 最短弯曲路径下各点对应关系Fig.5 One-to-one match in the shortest bending

由图5中的最佳对应关系确定的最佳弯曲路径图,如图6所示。

图6 最佳弯曲路径图Fig.6 The optimum bending path diagram

对于最短弯曲路径下的各点对应关系，存在以下几种情况[15]

①单点对应：Pi中的一个元素和Qj中的唯一元素相对应；

②多点对应：Pi中的一个元素和Qj中的多个元素相对应或Qj中的一个元素和Pi中的多个元素相对应。由弯曲路径的必要条件可知，Qj和Pi中的多个元素在时间序列上是连续的。

对于单点对应的情况，表明两时间序列有唯一最优解，两点已匹配成功。现在假设

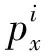
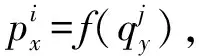
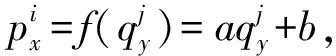
4 数据匹配实验及分析

4.1 数据匹配实验

对于前后两次测量的数据，首先经过坐标系的旋转和平移，将数据统一到同一坐标系下。为了保证后期匹配的高精度，则要判断两条曲线相似部分是否对齐，即是否完全统一在同一坐标系下。构造目标函数H(x)

(10)

其中，y为标准坐标系{o;x,y}下的函数，y′为通过坐标转换后的函数，n为测量曲线中的数据总量。旋转和平移量在迭代过程中不断变化，使目标函数H(X)的值不断变化，当目标函数H(X)值最小时，则判定为两条曲线相似部分对齐，此时的旋转和平移量认为最佳值。由实际测量可知，相邻两次测量的角度偏移量较小，虽然人为因素或环境因素引起的偶然误差存在，但对后期的匹配影响不大，故旋转和平移误差有较好的鲁棒性。

根据测量原理可确定相似波形段，利用动态时间弯曲算法求解出相似波形段中的单点对应关系，进而对数据进行匹配和处理。匹配流程图如图7所示。

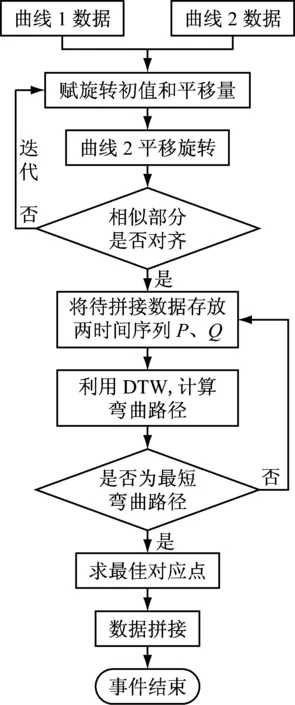
图7 短波匹配流程图Fig.7 Shortwave matching flow chart

匹配后的图像如图8所示。

图8 轨道波形匹配图Fig.8 Rail shortwave matching diagram

4.2 匹配算法的比较与评价

由动态时间弯曲算法原理及实现过程可知，最短弯曲路径下所对应的DTW值，间接反映了两条曲线的相似度即匹配的好坏。两曲线匹配的越好，其相似度越高，最短弯曲路径越短，对应的DTW数值越小；两曲线匹配越差，匹配曲线越不相似，最短弯曲路径越长，对应的DTW值也越大。理想情况下，两条匹配曲线完全匹配时求解的最短弯曲路径为0，即DTW值为0。

由文献[16-17]可知，传统匹配方法中常用的方法是基于区域的数据匹配，该算法通过求解曲线相关系数来实现。本文以传统匹配算法中的基于区域的匹配算法为代表，比较动态时间弯曲算法与传统匹配方法的匹配精度问题。对同一测量数据分别利用传统匹配算法和动态时间弯曲算法匹配，匹配图像如图9所示。

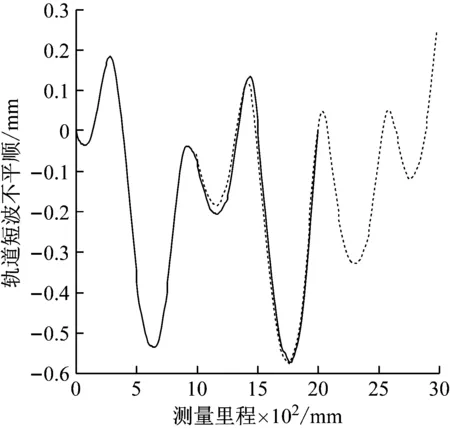
(a) 基于区域的传统算法匹配

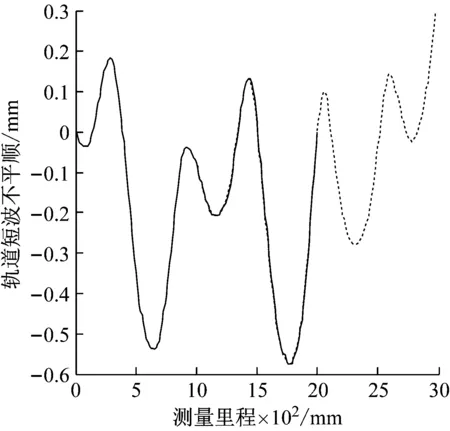
(b) 动态时间弯曲算法匹配图9 两种算法的波形匹配图Fig.9 Waveforms mosaic based on two algorithms

通过DTW距离计算式(7)～(9)可知，图9(a)的DTW值为0.012 4，图9(b)的DTW值为0.003 3。

利用平直尺对某段钢轨进行测量。为了不失一般性，在所测60组数据中分别利用传统匹配算法和动态时间弯曲算法进行曲线匹配，并求解匹配后所对应的DTW值。两种算法的DTW值如图10所示。

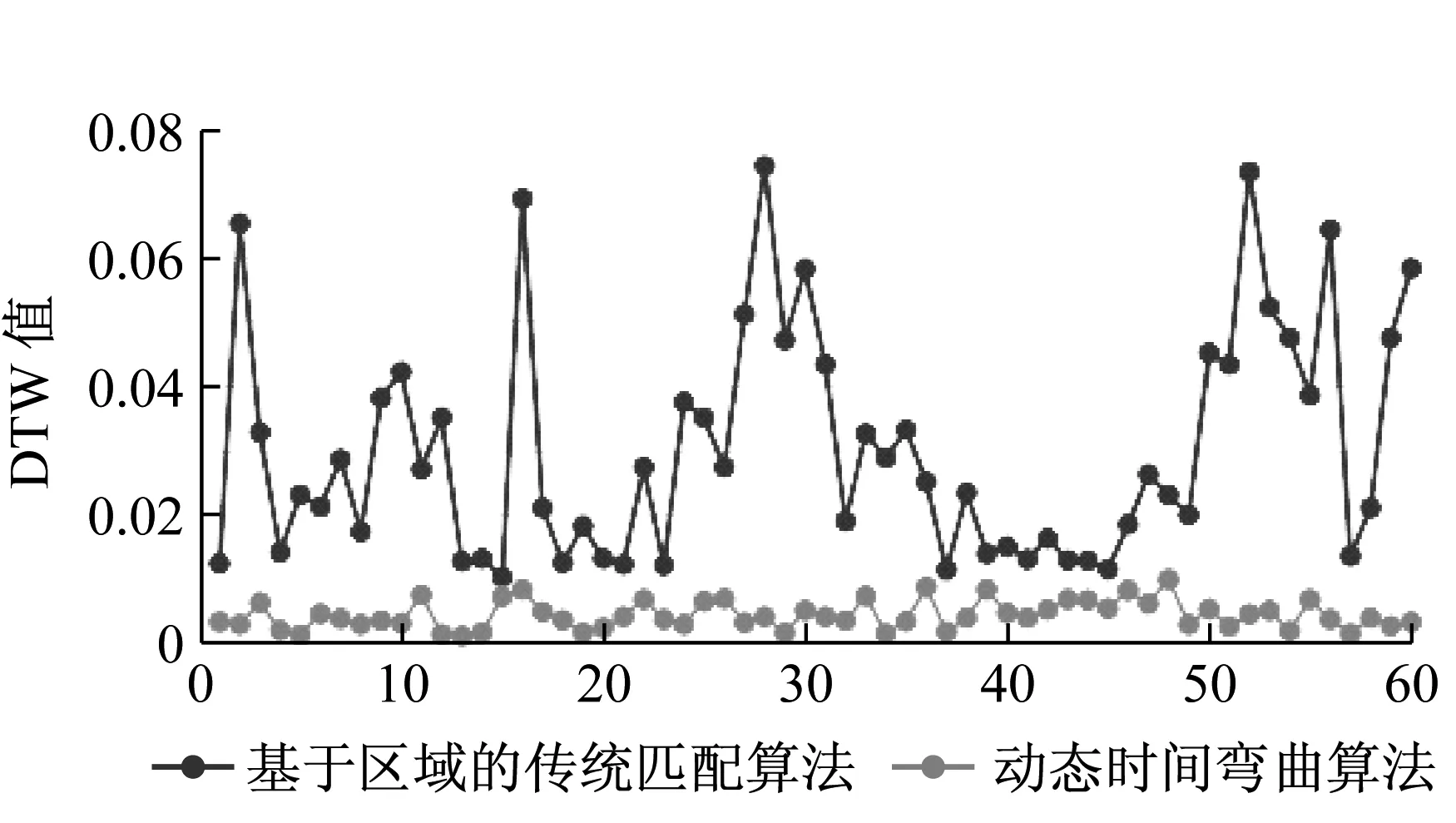
图10 两种算法的DTW值Fig.10 The value of DTW by using two algorithms

对以上60组数据进行数据统计分析，可求出两种算法下的DTW均值；对数据标准化处理后，可通过标准差的大小反映两种算法的稳定性[18]，如表1所示。

表1 两种匹配算法的数值统计Tab.1 Numerical statistics by using two algorithms

由表1可知，通过传统算法匹配所求得的DTW均值为0.030 2，约是动态时间弯曲算法匹配所得DTW均值(0.004 4)的10倍，即通过动态时间弯曲算法进行的数据匹配，匹配精度比基于区域的传统匹配算法的匹配精度提高约10倍，匹配效果比传统匹配算法好。并且，将两组数据标准化处理后所求得的标准差表明，利用动态时间弯曲算法进行的数据匹配，匹配稳定性较好，没有出现误差较大的情况。

5 结 论

本文基于动态时间弯曲算法对轨道波形进行匹配，通过构造累积代价矩阵，利用递归思想，可计算两条曲线的最短弯曲路径，并求出两条待匹配曲线之间的单点对应关系，从而进行数据点与点之间的精准动态匹配。将传统匹配中基于区域的匹配算法与动态时间弯曲算法作比较，实验结果表明：

(1)基于动态时间弯曲的匹配方法，解决了传统匹配方法中刚性匹配的问题。通过对横坐标轴的弯曲变形，可找到待匹配曲线的最佳匹配关系，实现精准的动态匹配。

(2)基于动态时间弯曲的匹配精度比传统匹配算法高约10倍，能较好的对测量数据进行匹配。

(3)基于动态时间弯曲算法下的DTW值标准差为0.248 1，比基于区域的传统匹配方法标准差小，故基于动态时间弯曲算法的匹配稳定性较好，可信度较高。

(4)本算法还可以运用在测量数据的重复性分析、钢轨轮廓匹配、测量曲线相似比较等方面。

参 考 文 献

[1] 程小红. 钢轨焊接接头平直度检测仪研制[D]. 成都: 西南交通大学,2010.

[2] YAN Ziquan, GU Aijun, LIU Weining, et al. Effects of wheelset vibration on initiation and evolution of rail short-pitch corrugation[J]. Journal of Central South University,2012(9):2681-2688.

[3] JELALI M.Performance assessment of control systems in rolling mills-application to strip thick thickness and flatness control[J]. Journal of Process Control, 2007,17:805-816.

[4] KONG W,KIMIA B B. On solving 2D and 3D puzzles using curve matching[C]∥Proceedings of the CVPR.Hawaii, USA,2001.

[5] UCOLUK G, TOROSLUL H. Automatic reconstruction of broken 3-D surface objects[J]. Computers and Graphics, 1999, 23(4):573-582.

[6] 余先川,吕中华,胡丹.遥感图像配准技术综述[J]. 光学精密工程,2013(11):2960-2972.

YU Xianchuan,LÜ Zhonghua,HU Dan.Reviwe of remote sensing image registration techniques[J].Optics and Precision Engineering, 2013(11):2960-2972.

[7] 牛小兵,林玉池,赵美蓉,等.基于特征的二维图像匹配法测量几何量[J].天津大学学报,2001(3):396-339.

NIU Xiaobing,LIN Yuchi,ZHAO Meirong, et al.Measurement of geometric parameters based on feature based image mosaic method[J].Journal of TianJin University,2001(3):396-399.

[8] 肖辉,胡运发. 基于分段时间弯曲距离的时间序列挖掘[J]. 计算机研究与发展,2005(1):72-78.

XIAO Hui,HU Yunfa.Data mining based on segmented time warping distance in time series database[J].Journal of Computer Research and Development,2005(1):72-78.

[9] 李正欣,张凤鸣,李克武,等. 一种支持DTW距离的多元时间序列索引结构[J]. 软件学报,2014(3):560-575.

LI Zhengxin,ZHANG Fengming,LI Kewu, et al.Index structure for multivariate time series under DTW distance metric[J].Journal of Software,2014(3):560-575.

[10] 邹朋成,王建东,杨国庆,等. 辅助信息自动生成的时间序列距离度量学习[J]. 软件学报,2013(11):2642-2655.

ZOU Pengcheng,WANG Jiandong,YANG Guoqing, et al. Distance metric learning based on side information autogeneration for time series[J]. Journal of Software,2013(11):2642-2655.

[11] 杨靖. 基于动态时间弯曲的时间序列相似性搜索技术的研究[D].哈尔滨:哈尔滨工业大学,2013.

[12] 邹朋成,王建东,杨国庆,等. 辅助信息自动生成的时间序列距离度量学习[J]. 软件学报,2013(11):2642-2655.

ZOU Pengcheng,WANG Jiandong,YANG Guoqing, et al.Distance metric learning based on side information autogeneration for time series[J].Journal of Software,2013(11):2642-2655.

[13] PREKOPCSAK Z,LEMIRE D. Time series classification by class-specific Mahalanobis distance measures[J]. Advances in Data Analysis and Classification, 2012,6(3):185-200.

[14] GHAREHBAGHI A, ASK P, BABIC A. A pattern recognition framework for detecting dynamic changes on cyclic time series[J]. Pattern Recognition, 2015, 48(3):696-708.

[15] 杜永峰,李万润,李慧,等. 基于时间序列分析的结构损伤识别[J].振动与冲击,2012,31(12):108-111.

DU Yongfeng,LI Wanrun,LI Hui, et al. Structural damage identification based on time series analysis[J]. Journal of Vibration and Shock,2012,31(12):108-111.

[16] 严大勤,孙鑫. 一种基于区域匹配的图像匹配算法[J]. 仪器仪表学报,2006(增刊1):749-750.

YAN Daqin,SUN Xin.Image mosaics algorithm based on area matching[J].Chinese Journal of Scientific Instrument,2006(Sup1):749-750.

[17] 顾费勇. 基于图像的自适应图像匹配算法研究[D].杭州:浙江大学,2008.

[18] 蒋瑜,陶俊勇,王得志,等. 一种新的非高斯随机振动数值模拟方法[J]. 振动与冲击,2012,31(19):169-173.

JIANG Yu,TAO Junyong,WANG Dezhi, et al. A novel approach for numerical simulation of a non-Gaussian random vibration[J].Journal of Vibration and Shock,2012,31(19):169-173.