涡扇发动机低压部件通流耦合计算
孙 逸,葛 宁,舒 杰
(南京航空航天大学能源与动力学院,南京210016)
0 引言
在航空发动机总体设计初期,通流方法可以快速得到发动机性能以及子午面流动特征[1-2],仍是现代航空发动机设计工作的基石和重要的设计工具[3-4]。Simon[5]提出基于Navier-Stokes方程的周向平均通流模型,实现适用于轴流压气机的定常与非定常通流计算,并对周向平均Navier-Stokes方程中出现的各种附加项做了详细论证;金海良[6]对某跨声速单级风扇、某子午加速风机和某跨声速双级风扇的研究表明,基于Navier-Stokes方程的周向平均通流模型计算得到的子午流场和径向参数分布与3维计算结果十分吻合,在近端壁区域具有较高的计算精度;周向平均通流模型的另一重要应用是发动机整机数值仿真计算,可用于发动机各部件间的流场匹配,研究发动机各部件间的相互影响[7];Friederike[8]针对某大涵道比涡扇发动机提出1种0D/2D耦合航空发动机性能预估方法;Denton等[9]基于40多年研究经验开发了多层次叶轮机械设计程序Multall,其中通流计算作为重要环节,可快速分析叶片损失和效率。由于现阶段受CFD技术和计算机性能的限制,采用3维数值模拟方法计算发动机整机需要大量的计算资源和时间,而采用通流计算方法能够节约计算时间,快速发现各部件匹配过程中的问题,具有一定的工程应用价值。本文选取某涡扇发动机低压部件为研究对象,采用通流模型耦合计算,研究各部件相互作用以及过渡段几何参数对发动机总体性能的影响。通流模型可用于发动机总体设计初期对发动机性能快速预估,实现各部件性能匹配。
1 基于Navier-Stokes方程的周向平均通流模型
在相对柱坐标系中,对Navier-Stokes方程进行周向平均[10],得到通流模型的控制方程为

其中

式中:Q为守恒量;F和H为对流(无黏)通量;Fv和Hv为扩散(黏性)通量;S为Navier-Stokes方程组在相对柱坐标系下导出的源项;SB为无黏叶片力项;Sv为黏性叶片力项;fB和fv分别为模化后的无黏叶片力和黏性叶片力;x、r、θ分别为轴向、径向和周向坐标方向;ρ为密度;v为相对速度;p为静压;e为单位质量总能;w为转速;τ为黏性应力;q为热流量;定义叶片堵塞系数

式中:θs和θp分别为叶片吸力面和压力面上的角坐标;N为叶片数。
堵塞系数b在叶片区小于1,在非叶片区等于1。基于无黏叶片力始终垂直于平均流面的假设,本文将无黏叶片力的求解分为2步[11-12]:(1)在动量方程中不计入无黏叶片力;(2)在动量方程中仅计入无黏叶片力,从而可以修正第1步求得的动量,使其与平均流面相切。这就避免了显式求解无黏叶片力。黏性叶片力的模化采用著名的分布损失模型[13],引入1种分布的体积力来计入流动损失的影响。黏性叶片力平行于相对速度并且反向,所作功仅产生熵增,采用总压损失系数计算叶排进口到出口熵增。本文采用时间推进的有限体积法求解上述控制方程,用具有较高间断分辨率的Roe通量差分分裂方法[14]对无黏对流通量进行离散,而黏性通量的离散则是利用网格中心的流场变量将网格面上的黏性通量表示出来,紊流模型采用B-L模型。
2 通流模型验证
通流耦合计算中首先要保证通流模型的准确性,激波位置和激波强度对压气机流量、效率均有较大影响。因此,选取NASA Rotor67和某3级风扇为验证算例。
2.1 Rotor67算例
Rotor67是1个低展弦比跨声速转子,Strazisar[15]于1989年做了细致的试验。设计转速为16043 r/min,设计转速下最高效率点流量为34.573 kg/s,压比为1.642,效率为0.93。最高效率点通流模型计算结果与试验值对比见表1,可见通流计算结果与试验值基本吻合。根据Strazisar的描述,由于在转子出口边界层处测点较少,试验测量的等熵效率可能偏高。

表1 Rotor67通流计算与试验结果对比
Rotor67在最高效率点时,通流模型计算得到的叶排出口截面参数(分别为气流角、总温、静压、总压)径向分布与试验值对比如图1所示。从图中可见,通流计算得到的静压分布与试验值十分吻合,但由于叶尖存在激波,气流角和总温在叶尖处与试验值有一定偏差。总压径向分布与试验基本吻合,而且能够预测出端壁附面层附近的总压变化趋势。
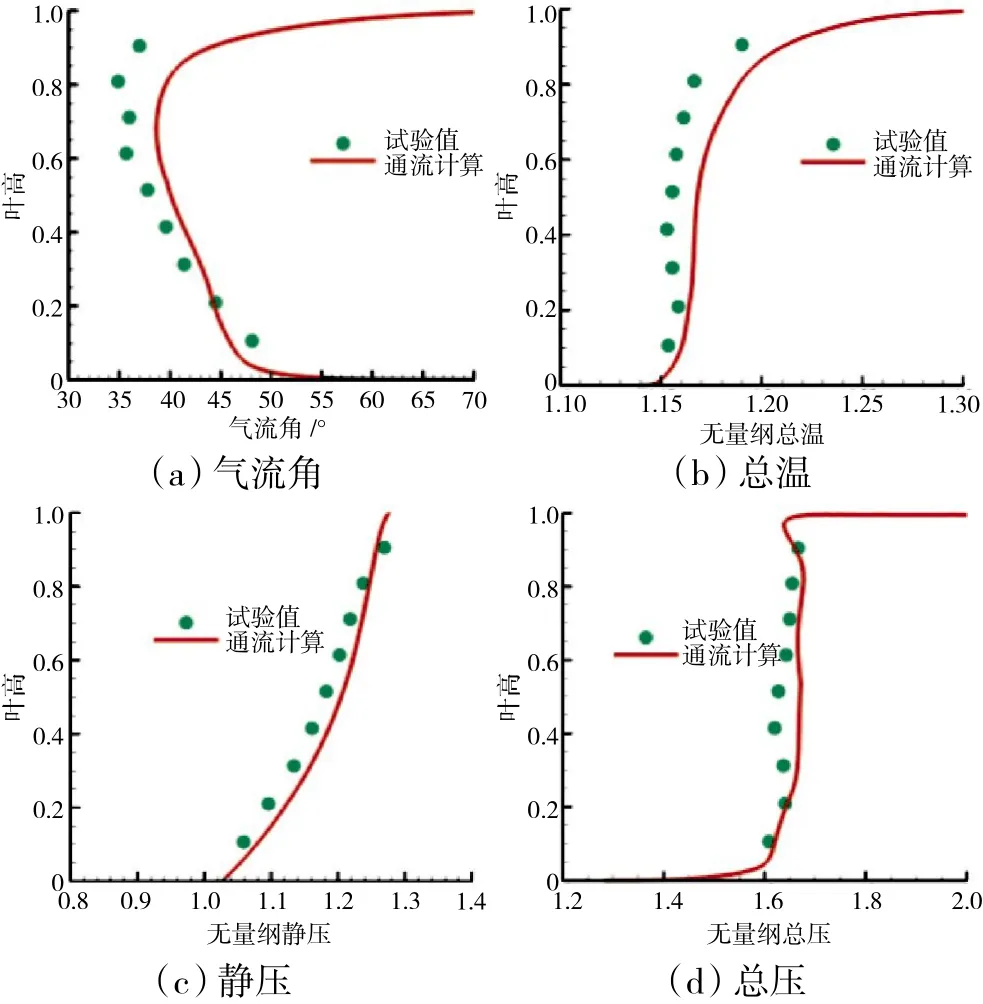
图1 Rotor67叶排出口径向参数分布
Rotor67在最高效率点的马赫数等值线如图2所示,从图中可见,叶片区域存在2道激波,第1道为叶尖进口斜激波,第2道为尾缘附近的正激波,波前马赫数约为1.4。通流计算得到的Rotor67在100%转速下的特性线如图3、4所示。从图中可见,二者结果基本吻合,验证了通流模型的准确性和可靠性。

图2 Rotor67最高效率点马赫数等值线

图3 流量-效率特性线

图4 流量-压比特性线
2.2 某轴流风扇算例
选取某带进口导叶的3级轴流风扇进行验证,其设计状态下压比为3.5,流量为81.0 kg/s。风扇子午流场相对马赫数如图5所示。从图中可见,第1级转子叶尖最高波前马赫数约为1.5,较强的激波使得叶尖压比相对试验值偏高,同时较强的激波-边界层相互干扰损失导致转子叶尖效率较低。
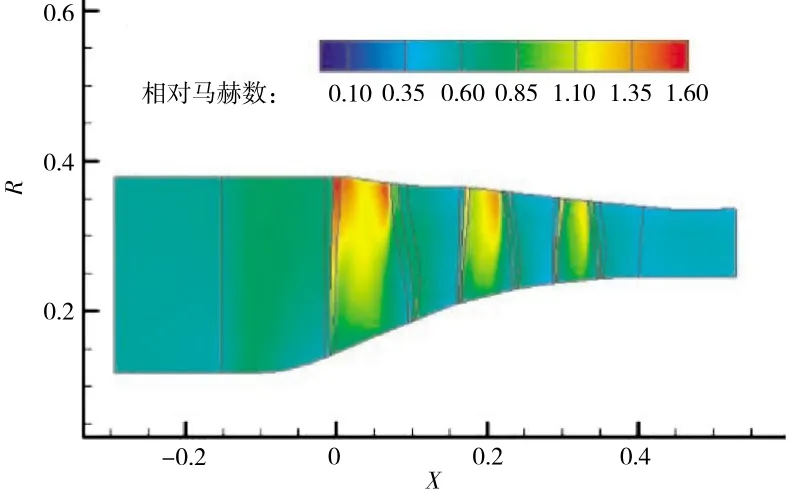
图5 风扇子午流场相对马赫数
计算了该轴流风扇在100%转速下的性能特性,并与试验值进行了对比,流量-效率特性线与流量-压比特性线分别如图6、7所示。从图中可见,在风扇近设计点计算得到的压比为3.53,效率为0.84。由于周向平均通流模型捕捉到的激波其物理本质与3维计算有所区别,因此捕捉到的激波比实际稍强,导致计算结果效率偏低。通流模型计算得到的特性线与试验值基本吻合,可用于多级压气机特性计算。

图6 风扇流量-效率特性

图7 风扇流量-压比特性
3 通流耦合计算
3.1 研究对象
选取某涡扇发动机除核心机3大部件外的低压部件为研究对象,包括进口带导叶的3级风扇、出口带支板的2级低压涡轮、内外涵道、掺混段以及尾喷管。其流道和叶型根据该发动机总体及部件性能参数试验值(见表2),采用流道设计程序计算得到。子午面流道如图8所示。风扇出口分为内外涵道2个计算域,并通过外涵道与涡轮后掺混段相连,掺混段下游为尾喷管。内、外涵冷热流体掺混是1个重要的气动热力过程,本文采用流量加权后定比热方法计算掺混后流场。耦合计算边界条件均按试验值给定,包括风扇进口总温、总压,内涵出口静压,低压涡轮进口总温、总压,喷管出口给定标准大气压力。

表2 通流计算结果与试验值对比

图8 几何模型子午面
3.2 计算结果及分析
计算结果表明,各部件单独计算时性能均能满足总体设计要求。但多个部件耦合数值计算时,发动机总体性能参数往往会偏离设计状态。本文通流耦合计算的核心就是研究各部件匹配以及过渡段对发动机总体性能的影响。
研究发现,风扇出口内、外涵分流板、涡轮出口掺混段整流板是影响部件匹配和发动机总体性能最重要的2个过渡段几何参数。分流板不仅分配内、外涵流量,控制涵道比,并且对风扇的工作状态有较大影响。掺混段整流板对内、外涵掺混有一定影响,而且可以抑制尾椎流动分离,对涡轮和喷管工作状态也至关重要。
通过调节分流板和整流板几何参数,使得各部件性能结算结果接近设计状态。通流计算子午流场相对马赫数如图9所示。从图中可见,风扇转子叶尖均存在激波,第1级转子中波前马赫数约为1.4,较强的激波损失使得风扇效率计算结果偏低3.57%。

图9 子午流场相对马赫数
从表2列出的风扇、低压涡轮、内外涵以及尾喷管近设计点性能参数与试验值对比可见,风扇计算流量偏大3.14%,增压比偏小0.56%,效率偏低3.57%。低压涡轮计算流量偏大4.93%,落压比偏大0.92%,效率偏低3.41%。通流模型得到的内涵流量偏大2.28%,外涵流量偏小0.48%,导致涵道比偏小2.55%。喷管出口计算流量和排气速度比试验值偏大,导致发动机计算推力比试验值偏大2.67%,耗油率偏低2.52%。从误差分析来看,本文通流耦合计算在近设计点能够满足发动机总体性能初步要求,最大误差不超过5.0%。
4 结论
本文通过对某涡扇发动机低压部件通流耦合计算,得到如下结论:
(1)采用周向平均通流模型对Rotor67和某3级风扇进行了计算并与试验值对比,结果证明通流模型能够正确捕捉激波强度与位置,预测的部件特性曲线趋势与试验基本吻合。
(2)对某涡扇发动机风扇、低压涡轮、内外涵道、掺混段和尾喷管等部件进行了通流耦合计算,研究了各部件匹配与过渡段几何参数对发动机总体性能的影响,在设计状态下发动机沿程各截面计算特征参数与试验值最大误差不超过5.0%。
(3)对比分析发现,风扇出口分流板控制涵道比并对风扇性能有一定影响。涡轮出口掺混段整流板对风扇和低压涡轮性能均有较大影响。通过调节过渡段几何参数,实现各部件性能匹配,达到发动机总体性能要求。
该通流模型能够快速预估发动机总体性能,发现各部件匹配中存在的问题,具有一定的工程应用价值。内、外涵掺混段涉及变比热问题,本文采用内、外涵流量加权平均比热比,喷管出口总温平均值比试验值偏高3.5%。掺混段计算有待进一步完善,使喷管温度场与实际情况更加吻合。
[1]Smith L H.The radial-equilibrium equation of turbomachinery[J].ASME Journal of Engineering for Power,1966,88(1):1.
[2]Jin H L,Jin D H,Li X J.A time-marching throughflow model and its application in transonic axial compressor [J].Journal of Thermal Sinence,2010,19(6):519-525.
[3]Denton J D,Horlock J H.A review of some early design practice using computational fluid dynamics and a current perspective[J].Journal of Turbomachinery,2005,127(1):5-13.
[4]Denton J D,Dawes W N.Computational fluid dynamics for turbomachinery design[J].Archive Proceedings of the Institution of Mechanical Engineers,1998,213(2):107-124.
[5]Simon J F,Leonard O.Modeling of 3D losses and deviations in a throughflow analysis tool[J].Journal of Thermal Science,2007,16(3):208-214.
[6]金海良.周向平均方法在多级轴流风扇/压气机设计与分析中的应用[D].北京:北京航空航天大学,2011.JIN Hailiang.Application of circumferentional average method in multistage axial fan/compressor design and analysis[D].Beijing:Beijing University of Aeronautics and Astronautics,2011.(in Chinese)
[7]Wan K,Jin H,Jin D.Influence of nonaxisymmetric terms on circumferentially averaged method in fan/compressor[J].Journal of Thermal Science,2013,22(1):13-22.
[8]Mund F C,Doulgeris G,Pilidis P.Enhanced gas turbine performance simulation using CFD modules in a 2D representation of the low-pressure system for a high-bypass turbofan [J].Gas Turbines Power,2006,129(3),761-768.
[9]John D Denton.Multall-an open source,CFD based,turbomachinery design system[R].ASME 2017-GT-63993.
[10]Baralon S,Eriksson L E,Hall U.Evaluation of higher-order terms in the throughflow approximation using 3D Navier-Stokes computations of a transonic compressor rotor[R].ASME 1999-GT-074.
[11]Gentry R A,Martin R E,Daly B J.An eulerian differencing method for unsteady compressible flow problems[J].Journal of Computational Physics,1966,1(1):87-118.
[12]宁方飞.考虑真实几何复杂性的跨音压气机内部流动的数值模拟[D].北京:北京航空航天大学,2002.Ning F F.Numerical investigations of flows in transonic compressors with real geometrical complexities[D].Beijing:Beijing University of Aeronautics and Astonautics,2002.(in Chinese)
[13]Bosman C,Marsh H.An improved method for calculating the flow in turbomachines,including a consistent loss model[J].Archive Journal of Mechanical Engineering Science,1974,31(16):25-31.
[14]Roe P L.Approximate riemann solvers,parameter vectors,and difference schemes.[J].Journal of Computational Physics,1981,43(2):357-372.
[15]Strazisar A J,Wood J R,Hathaway M D.Laser anemometer measurements in a transonic axial-flow fan rotor[J].NASA STI/Recon Technical Report N,1981,90(2):430-437.

