无源器件噪声标准值计算方法的研究
吴爱华, 刘 晨, 王一帮, 梁法国
(中国电子科技集团公司 第十三研究所, 河北 石家庄 050051)
1 引 言
美国Keysight公司基于PNA-X矢网可以提供50 GHz的噪声系数测量能力,其主要测量原理是:应用噪声参数原理进行噪声选件的校准和被测件的测量[1,2],该方法称作“源端失配修正的冷源法”,其准确度高于传统的“Y因子法”。
新的噪声测量方法给校准工作带来了挑战,2014年,杨婷对比了主流仪器的噪声系数测量方法,指出矢网噪声选件的测量方法不同于“Y因子”法[3],因此,JJF 1460—2014《噪声系数分析仪校准规范》[4]等计量规程,无法指导其校准。2015年,王成报道了矢网中噪声选件的溯源问题,提出采用矢网校准过程中的功率计和噪声源建立溯源途径[5];但是,这种方案忽视了复杂的噪声测量模型对测量结果的作用,无法提供直观判断噪声测量效果的方法。为了解决矢网中噪声选件的计量问题,Ali Boudiaf等人报道的以无源器件为媒介进行噪声参数和噪声系数量传的方法值得借鉴[6,7],该方法的核心工作是提供无源器件的噪声标准值。
本文在分析现有方法的基础上,提出一种无源器件噪声标准值的矢量计算方法,以此推动高准确度矢网中噪声选件的计量工作。
2 噪声标准值的含义
“源端失配修正的冷源法”首先要测量DUT的噪声参数;然后计算获得50 Ω条件下定义的噪声系数。因此,为了完整解决矢网中噪声选件的计量问题,无源器件的噪声标准值计算包括噪声参数和噪声系数两部分工作。
Friis H T提出了噪声系数的概念[8],对噪声系数的定义为:对于1个线性两端口网络,规定输入端处于290 K时,其噪声系数是指输入端的信噪比除以输出端的信噪比。从定义看出,噪声系数是在从50 Ω的源端输入到50 Ω的负载条件下定义的。
但是依据噪声参数原理,任何器件的噪声系数会随源阻抗变化,其函数关系(也称为噪声参数方程)如式(1)所示:
(1)
式中:F为噪声系数;Fmin为最小噪声系数;Rn为等效噪声电阻;ΓS为源反射系数;Γopt为最佳源反射系数。
噪声参数分别为最小噪声系数、等效噪声电阻、最佳源反射系数的幅值和相位,在获得4个噪声参数前提下,可以非常方便地计算任何阻抗状态下的噪声系数,包括Friis提出的50 Ω匹配条件的下噪声系数。
3 现有计算方法分析
3.1 标量方法
设无源器件的衰减器量为A,Tα为环境温度,T0为标准噪声温度(等于290 K),则其噪声系数F可由式计算获得,当Tα=T0=290 K时,F=A。即匹配无源器件的噪声系数数值约等于衰减量量值,一般情况A近似等于S21。因此,F≈S21,依据此算法
(2)
该方法是一种计算简单且使用广泛的“噪声系数标准值”计算方法。
3.2 矢量方法
矢量方法的输入量是无源器件的4个S参数,输出量是4个噪声参数,进而也可以求解50 Ω匹配条件下的噪声系数。该功能集成在国外一些噪声参数测量系统开发商(如美国Maury公司)的测量软件中,用于验证其产品的测量准确度,但是理论计算模型未对外公布。
3.3 方法对比
标量法使用广泛,包含温度的影响量,但是只能提供单一的噪声系数标准值。矢量方法考虑了失配误差对于噪声标准值计算的影响[9~11],准确度较高,而且计算的噪声标准量值更加完整(噪声参数和噪声系数),但是只能计算标准噪声温度290 K下的结果,欠缺环境温度对于噪声标准值的影响。
为了量化对比2种方法的计算效果,设计如下试验:无源器件选择“25 Ω失配空气线级联6 dB衰减器”,频率为1~18 GHz,环境温度为290 K。
图1给出上述2种方法计算标准噪声系数量值的情况,其中ΔF为标量法与矢量法的计算结果之差。从图1中可以看出,标量法的计算结果普遍高于矢量法的计算结果,即ΔF≥0。在匹配点,即驻波比(VSWR)约等于1的频点,2个算法结果非常接近,但是驻波比约等于4的频点,标量法的计算结果比矢量法大了0.09~0.10 dB,因此,可以认为矢量方法对于失配条件的无源器件更加敏感,最大变化达到0.1 dB。
鉴于标量方法可以给出不同温度下的噪声标准量值,采用标量方法计算上述“无源器件”在温度为297 K和290 K时的噪声系数标准值对比试验,其中ΔF为标量法的297 K与290 K的差值。从图2中可以看出,环境温度升高噪声系数计算结果一定在增大,即ΔF>0;另一方面被测件的驻波比(VSWR)范围从1变化到4,ΔF的变化约为0.13~0.18 dB。
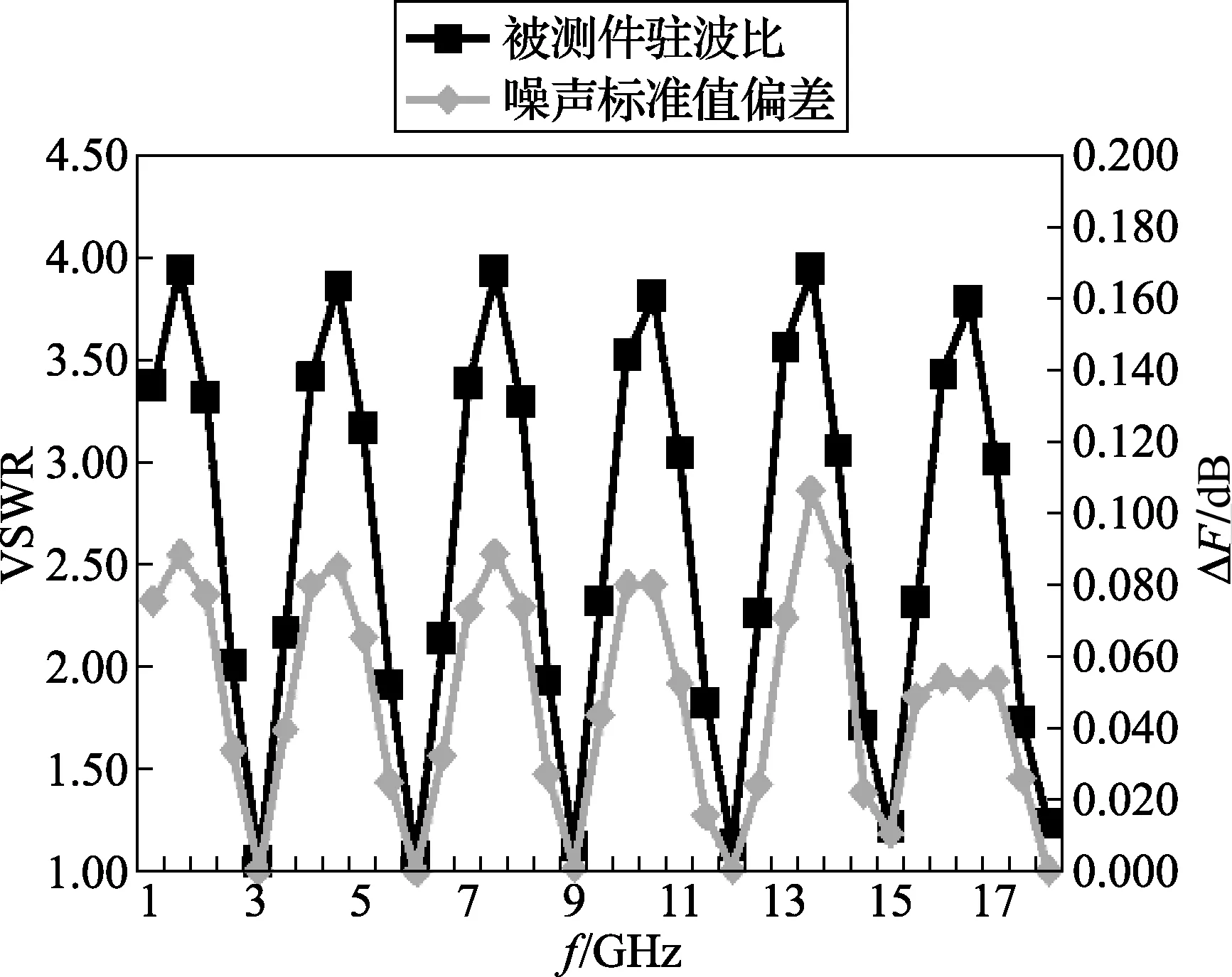
图2 标量法297 K和290 K时的噪声系数测量偏差
综上分析,矢量方法对于失配条件下的无源器件的噪声计算更加准确,准确度提升大约为0.95 dB(平均值)。
标量方法对于不同温度条件的噪声计算更加准确,对于试验中的2个温度设定值而言,准确度大约提升0.15 dB(平均值)。因此,为了实现通用的计算方法,需要结合现有方法的优点,开展含有温度信息的矢量方法研究。
4 矢量计算模型
模型建立过程如下:首先由无源器件的S参数和环境推导获得噪声相关矩阵;其次由噪声相关矩阵获得无源器件的噪声参数;最后由噪声参数计算获得噪声系数标准值。具体推导过程如下。
无源器件噪声模型的主要原理是将其视为一个传输参数T表征的无噪声的网络和在输入端口两个本征噪声波cT1和cT2。其矩阵表示如式(3)所示,其中ai和bi分别表示i(i=1,2)端口的信号输入波和反射波。一般情况,矢量噪声源由一个噪声相关矩阵CT表示,如式(4)所示。
(3)
(4)
为了符号使用和计算方便,确定如下定义:
kBW1=〈|cT1|2〉,kBW2
=〈|cT2/S21|2〉,kBW12
=〈cT1(cT2/S21)*〉
式中:kB是玻尔兹曼常数;W称之为等效噪声参数,量纲为热力学温度K。
所以,
(5)
对于一个无源器件的线性两端口网络,其噪声主要由热噪声产生,根据Bosma’s原理(假设热力学平衡情况下),无源器件的噪声相关矩阵如式(6)所示:
CT=kBT(E-SS+)ij
(6)
式中:T是无源器件的噪声温度,量值等于无源器件物理温度(即环境温度Tα);E表示单位矩阵;S+表示无源器件S参数的共轭矩阵。
然而,噪声相关矩阵与噪声参数的数学关系如式(7)所示:
(7)
所以,可以得到噪声参数与W参数的数学关系,如式(8)~式(10)所示。
(8)
(9)
(10)
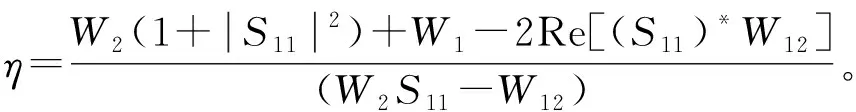
至此,就完成验证S参数和温度到噪声参数的理论计算。
获得噪声参数之后,在式(1)中,令ΓS=0,则可以求得无源器件的噪声系数标准值。
5 实 验
选择25 Ω失配空气线级联6 dB衰减器作为无源器件,采用Agilent公司电子校准件,校准后的Agilent公司PNA-X矢量网络分析仪,进行无源器件S参数的测量,环境温度选择不确定度为0.1℃的温度计进行测量。
5.1 模型验证
美国Maury公司在其商业软件中集成了无源器件S参数转换噪声系数的功能,但是其环境温度假定为标准噪声温度(290 K)。本文提出的算法与商业软件相比,最小噪声系数的最大偏差为±5×10-5dB以内,如图3所示;等效噪声电阻最大偏差为10-3量级,最佳源反射系数幅值的最大偏差为10-5量级,最佳源反射系数相位的最大偏差为10-3量级,噪声系数的最大偏差为10-5量级,这些量值都小于Maury公司软件算法的最小分辨力,即2种方法得到的结果一致性非常好。
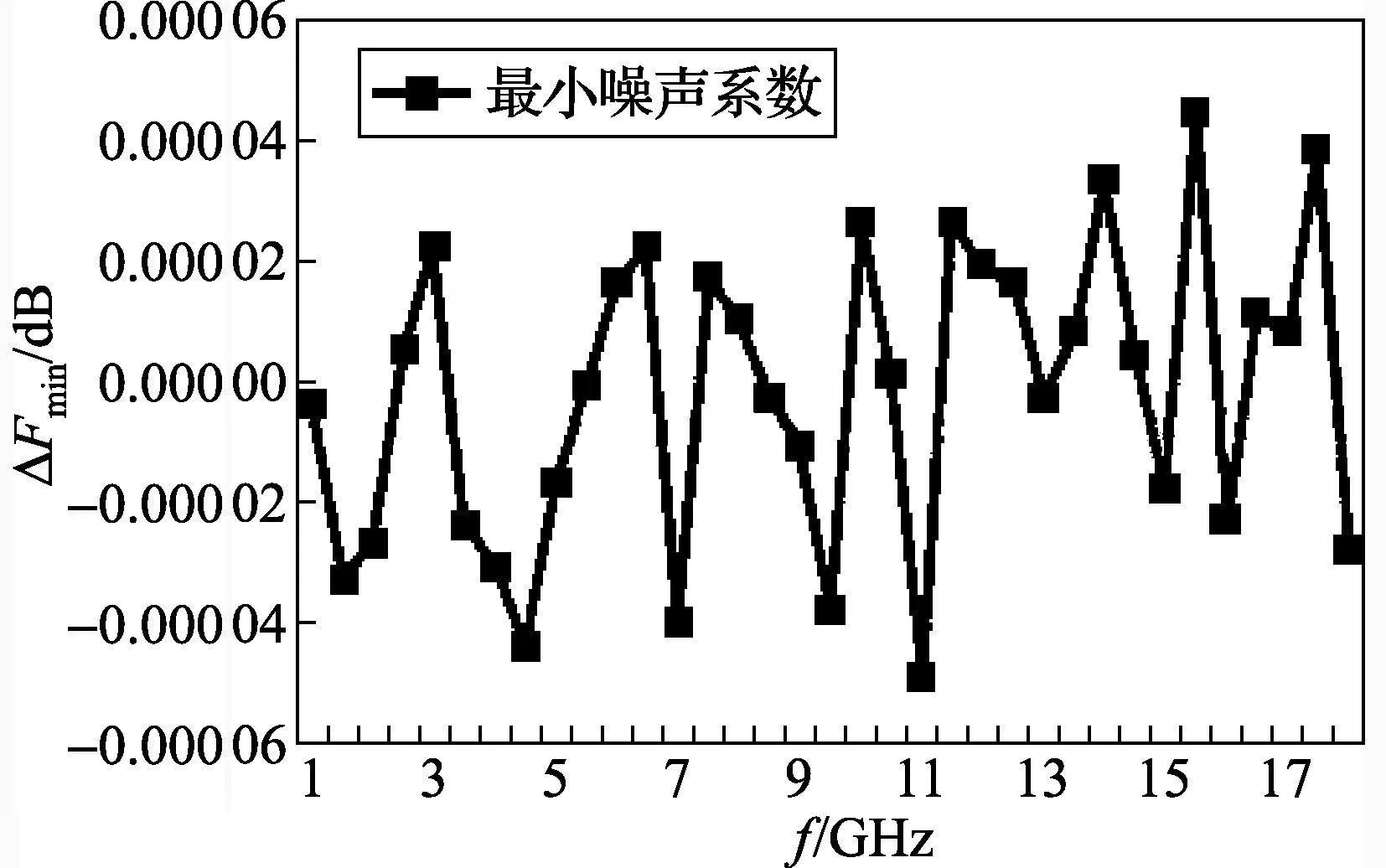
图3 “最小噪声系数”标准值的偏差
5.2 温度的影响
众所周知,噪声与温度密切相关,因此在无源器件计算噪声标准值的模型中必须包含温度参数。选择实验室噪声测量常用环境温度297 K与标准噪声温度290 K进行试验比较。图4给出了最小噪声系数的计算数据,其中ΔFmin表示297 K与290 K的计算结果之差,可以看出ΔFmin在0.0783 ~0.0814 dB之间变化,恒为正值,这种现象表明随着温度升高,最小噪声系数单调递增,这是符合物理本质的合理实验结果。图5给出2种温度下等效噪声电阻的变化,相比于290 K温度下,最大偏差由10-3变大了3个数量级。图6给出了噪声系数标准值在297 K与290 K温度下,其计算结果相差在0.079 ~0.089 dB之间。通过实验也证明了温度对于最佳源反射系数的幅值和相位几乎没有影响。
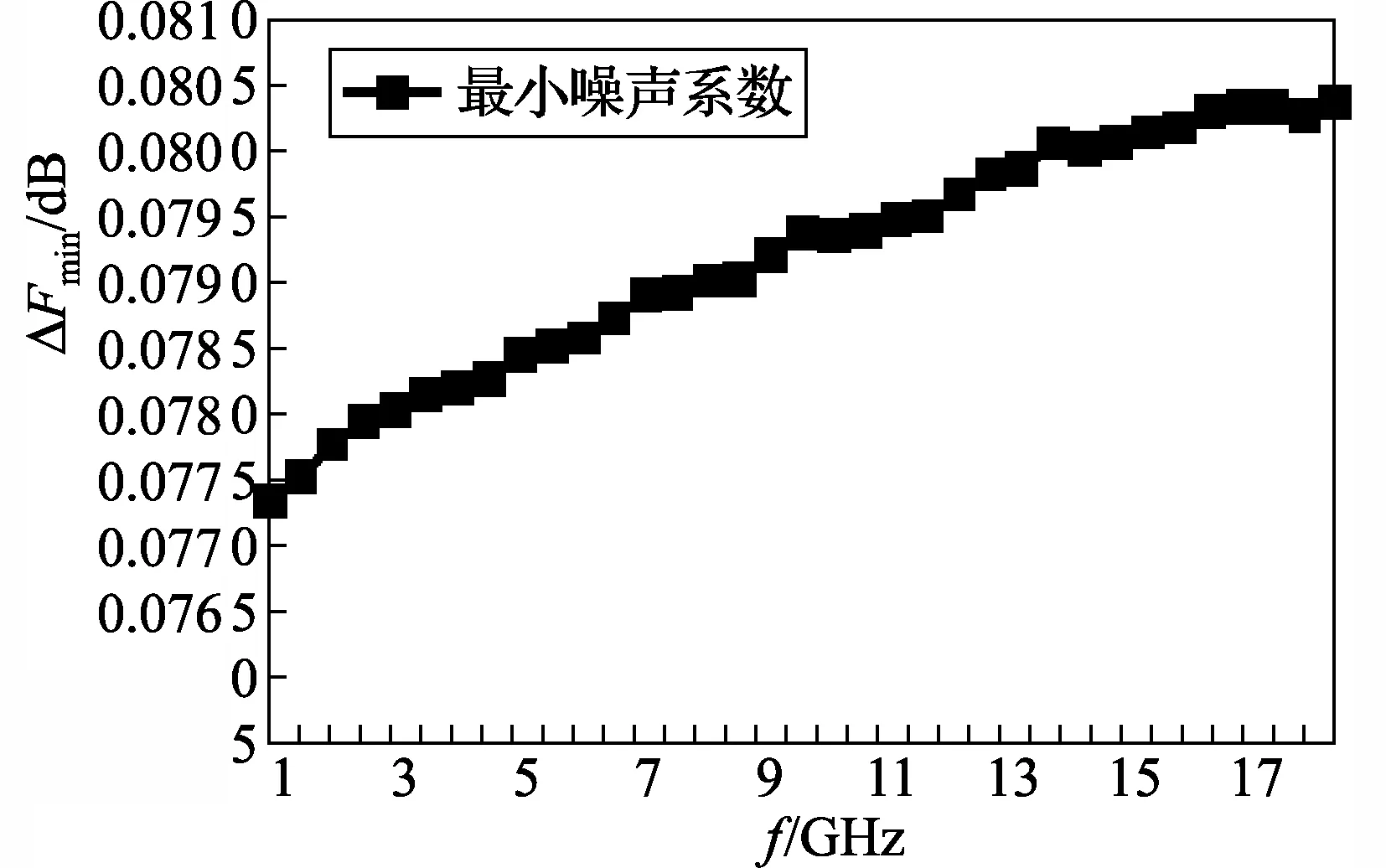
图4 2个温度下“最小噪声系数”标准值的差异
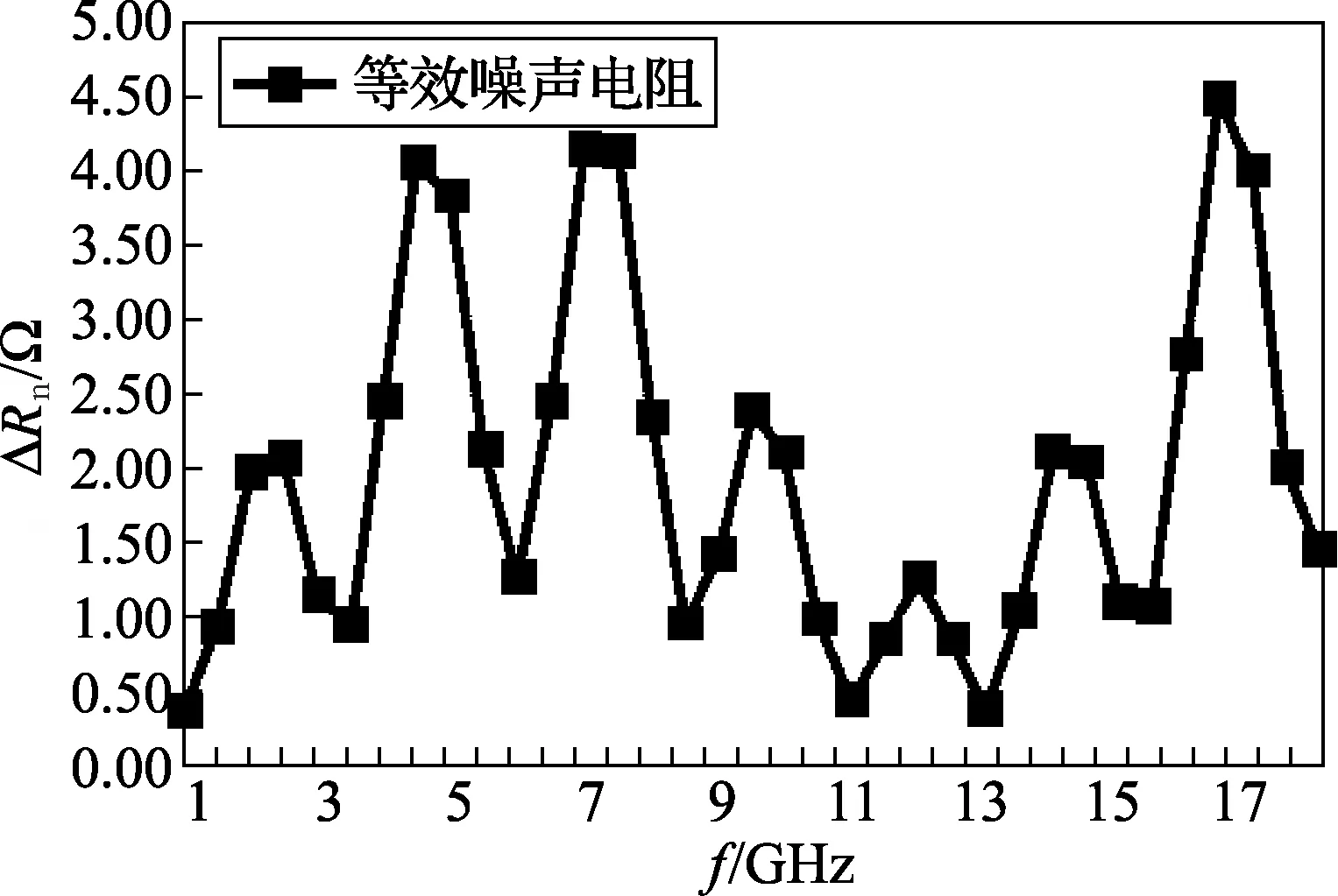
图5 2个温度下“等效噪声电阻”标准值的差异
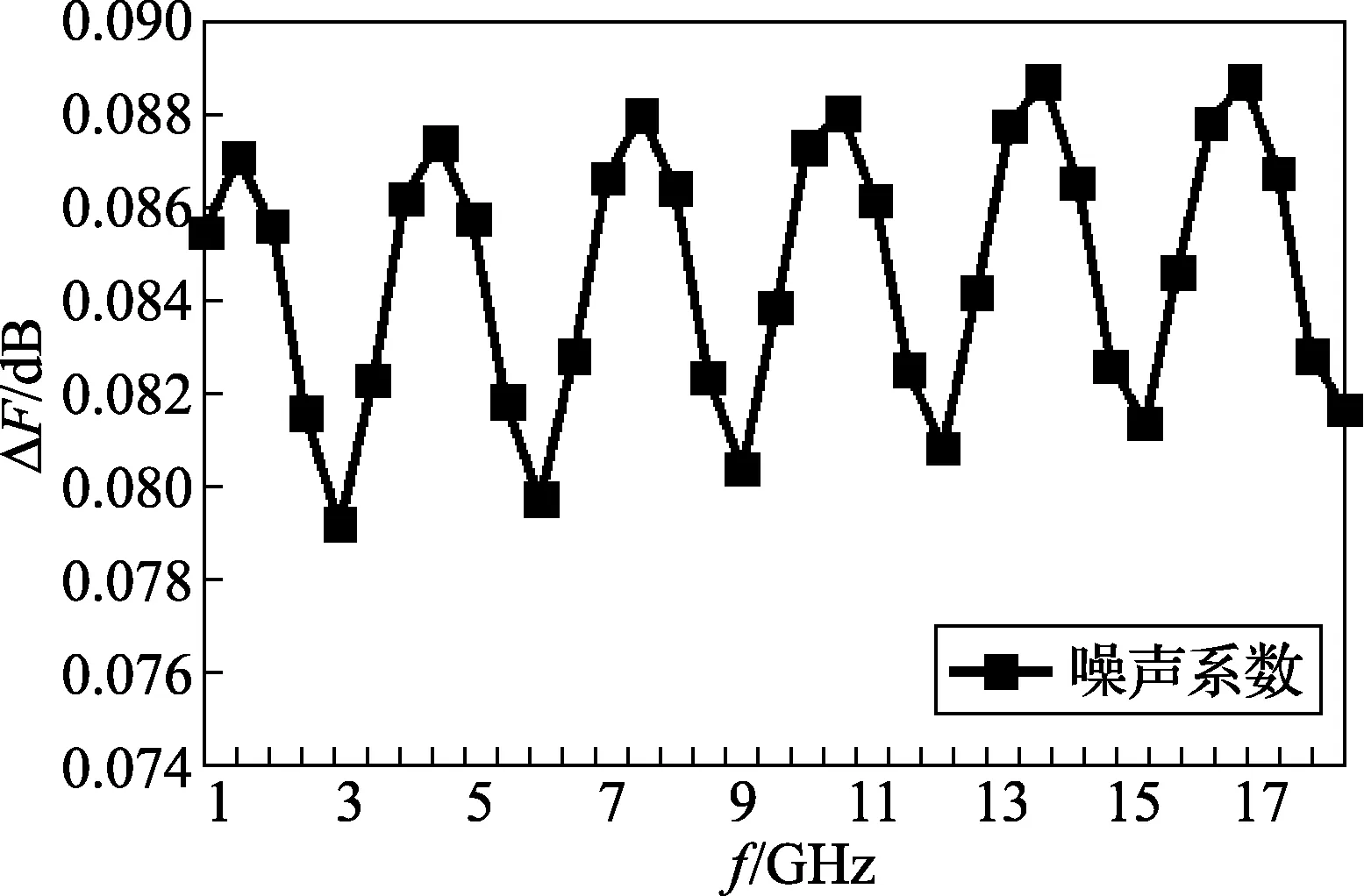
图6 2个温度下“噪声系数”标准值的差异
6 结 论
本文提出了一种基于无源器件噪声模型的噪声标准值计算方法。该方法吸收了现有方法的优点,通过实验对比,该方法适用于各种温度和失配条件的无源器件噪声标准值计算,在标准噪声温度(290 K)下,准确度与商业化软件相当,在常用测量环境温度(297 K)下,准确度明显提升。因此,本文所述工作对同行具有参考和借鉴价值,有助于推动矢网中噪声选件的校准工作。
[参考文献]
[1] 吴爱华, 梁法国, 刘强,等.微波低噪声封装器件噪声参数测量技术[J].半导体技术,2013,38(4):79-83.
[2] Paper W. High-accuracy Noise Figure Measurements Using the PNA-X Series Network Analyzer[Z]. Agilent Technologies, 2010.
[3] 杨婷. 不同仪器对噪声系数测量的方法[J].黑龙江科技信息,2014,(34):80-82.
[4] 国家质量监督检验检疫总局.JJF1460—2014噪声系数分析仪校准规范[S].北京:中国标准出版社,2014.
[5] 王成,李凯峰,宋晓婵,等. PNA,ZVA系列矢网在多参数计量方面溯源探讨[J].计测技术,2015,35(s1):213-216.
[6] Escotte L,Plana R,Graffeuil J.Evaluation of noise parameter extraction methods[J].IEEETransMicrowaveTheoryTechnol,1993,41(3):382-387.
[7] Boudiaf A,Dubon-Chevallier C,Pasquet D.Verification of on wafer noise parameter measurement[J].IEEEtransactionsoninstrumentationandmeasurement,1995,44(2):332-335.
[8] Friis H T. Noise figure of radio receivers[J].ProceedingsofIre, 1944,32(7):419-422.
[9] 周求湛,王树勋,戴逸松.N级微波四端网络的噪声参数计算[J].计量学报,2004,25(1):70-75.
[10] 梁伟军,高秋来.噪声源测量中修正转接头误差的一种方法[J].计量学报,2011,32(5):463-465.
[11] 高申翔,霍莹,崔豹,等.噪声传递中失配误差的再讨论及解决方案[J].计量学报,2016,37(5): 540-543.

