基于轧件水平振动的轧机辊系振动补偿模型
刘 彬, 姜甲浩, 刘 飞, 刘浩然, 李 鹏
(1. 燕山大学 电气工程学院, 河北 秦皇岛 066004; 2. 燕山大学 信息科学与工程学院, 河北 秦皇岛 066004)
1 引 言
轧机辊系的振动特别是轧机辊系的垂直振动,是冷轧带钢产品生产效率低下问题的关键所在[1]。轧机辊系的振动会在轧件表面产生明暗相间的振纹,可能造成轧制产品出现厚度误差,影响了轧制产品的质量和轧制速度的提高[2,3]。
近年来,针对轧机辊系垂直振动的问题,国内外学者从多种角度做过研究。Nizio J等通过建立两自由度轧辊质量块-弹簧-阻尼器模型,研究了轧件入口速度和压下率等因素对轧机辊系垂直振动的影响,得到了轧机辊系振动时的轧件临界入口速度和压下率[4];范小斌等通过引入Duffing振子和参激刚度项,建立了轧机辊系垂直振动模型,研究了轧机辊系振幅在非线性参数变化下的分岔特性[5];文献[6]从液压缸分段非线性的角度研究了液压缸非线性刚度和阻尼对轧机辊系垂直振动的影响;王桥医等研究了由于辊缝不稳定润滑条件下导致轧机辊系垂直振动的问题,得出了振动临界速度和辊缝润滑条件的关系[7];文献[8]考虑轧件和轧辊间的相互作用,建立基于辊缝动态摩擦方程的轧机辊系垂直振动模型,研究了轧件-轧辊工作界面动态摩擦机制影响下的冷轧机辊系垂振机理及系统稳定性。尽管研究人员从轧机结构简化、轧制工艺参数选取、工作界面润滑条件分析等多个角度对轧机辊系振动做了系统的研究,但是由于辊缝间轧件水平振动的不易观测性,由其引起的轧机辊系垂直振动现象常常被忽略,这在一定程度上削弱了模型的计算精度和准确性。为了更加真实地反映实际工况,必须对轧机辊系振动模型进行补偿。
本文考虑由于辊缝间轧件水平振动带来的工作界面摩擦力和轧制力的非线性特性,建立了基于轧件水平振动的轧机辊系振动补偿模型,仿真分析了不同轧辊转速下的轧机辊系振动规律。通过模型补偿前后轧制力理论值与现场实际数据对比,验证模型的有效性。
2 考虑轧件水平振动速度补偿的轧制力计算公式
由于影响轧制力的因素多种多样,所以有多种形式的轧制力计算公式,其中Hill公式应用最为广泛且具有较好的计算精度,为此采用Hill公式计算轧制力[9]:
F=BlcQpKTK
(1)
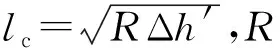
(2)
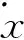
(3)
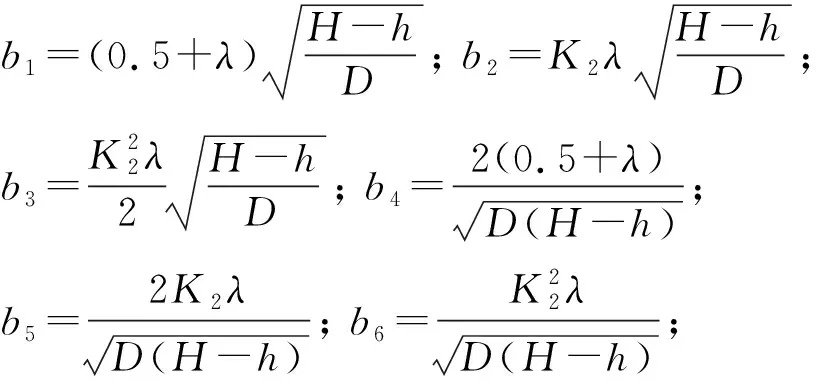
λ=(K1-0.5)e-K2v0。
为了方便后面动力学分析,将摩擦因数表达式分为不变部分和变化部分;
(4)
F=F(0,0)+ΔF
(5)
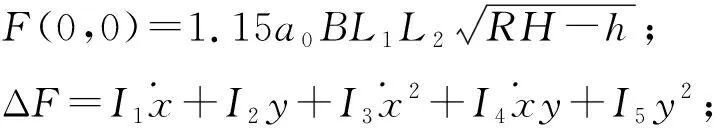
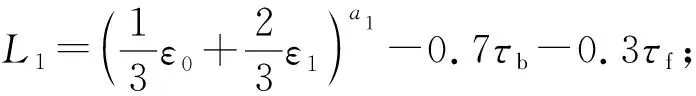
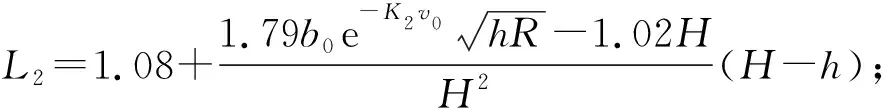
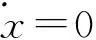
以上得到的摩擦因数公式和轧制力计算公式是后面分析轧机辊系动力学特性的基础。
3 轧机辊系振动模型
轧机系统结构复杂,为了方便研究,一般采用集中质量法对轧机结构机构进行等效和简化[3,9]。为此,采用集中质量法分别将上下部辊系的工作辊和支撑辊等效为一个质量块单元,在质量块-弹簧-阻尼经典模型基础上,考虑辊缝轧件动力学特性对轧机辊系振动的影响,建立如图1所示的板带轧机结构动力学模型。
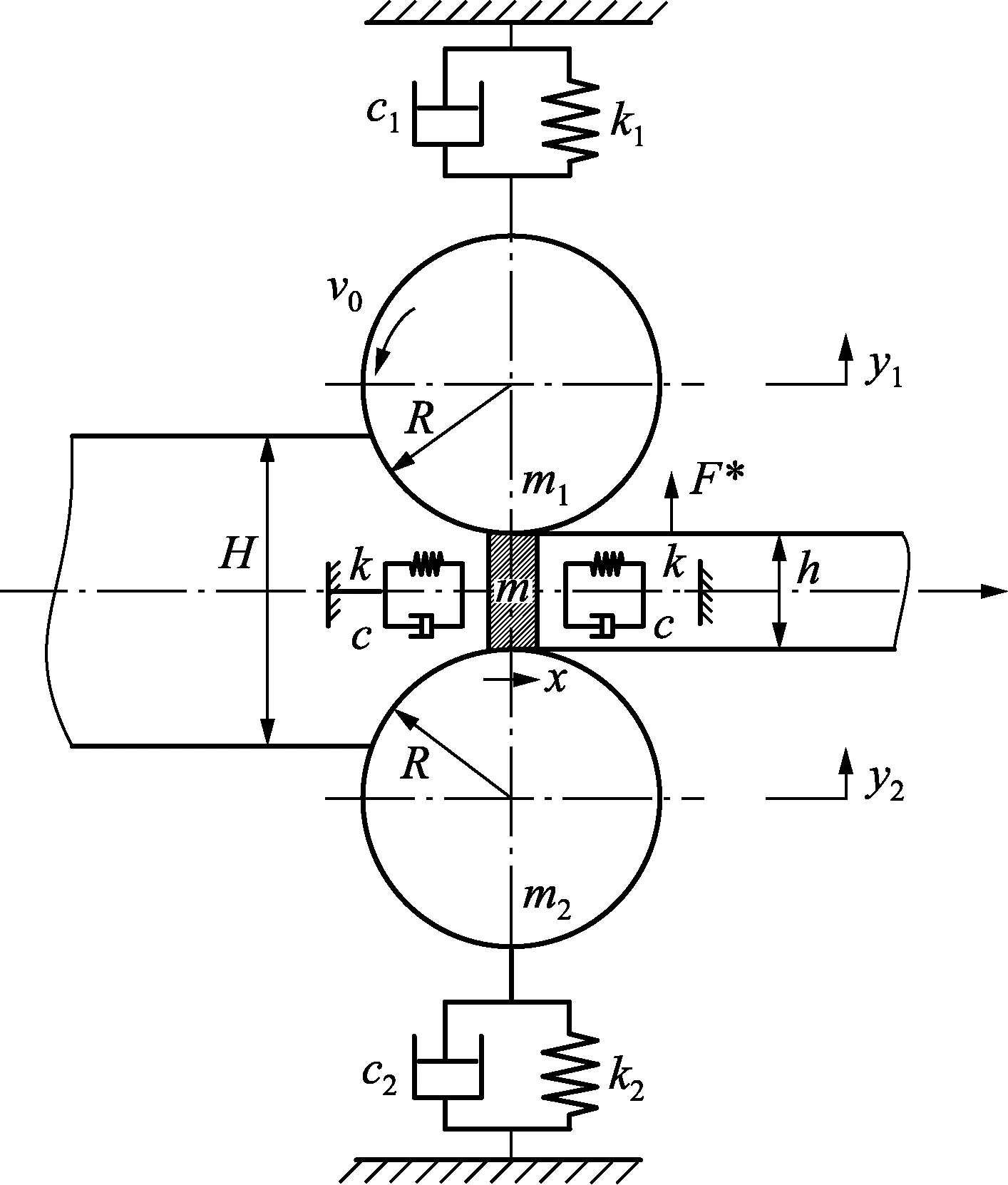
图1 板带轧机结构动力学模型
图1中m为辊缝部分轧件质量,m=ρV=(ρlc(H+h)/2;将前后滑区张力的波动等效为2个刚度为k的力函数,k=σS/L,σ为预加张力,S为轧件的横截面积,L为轧件由于外加张力所产生的变
形长度;将轧件和轧辊间的阻尼效应等效为2个阻尼系数为c的阻尼模型;m1和m2分别为上、下部辊系的等效质量;k1和k2分别为上、下部辊系与机架上、下横梁间的等效刚度;c1和c2分别为上、下部辊系与机架上、下横梁间的等效阻尼;R为轧辊半径;v0为轧辊转速;y1和y2为上、下部辊系的振动位移;H为轧件入口厚度;h为轧件出口厚度;F*为轧辊受到的外部扰动力。
根据广义耗散的Lagrange原理,轧辊在垂直方向上的动力学平衡方程为:
(6)
考虑轧机上下部辊系的结构和振动特性的对称性,有m1=m2;c1=c2;k1=k2;y1=-y2。这样式(6)中的2个方程就具有相同的表达形式[9]。为简化分析步骤,就轧机上部辊系进行分析,且令M为上部辊系的等效质量;K为上部辊系与机架上横梁间的等效刚度;C为上部辊系与机架上横梁间的等效阻尼;所以式(6)可以表示为:
(7)
由于在冷轧过程中轧辊接近于完全弹性压扁,即轧辊与轧件的接触面近似为平面,因此可以忽略轧件受到的摩擦力在垂直方向上的分力,在此基础上构造轧件水平振动的动力学平衡方程:
(8)
式中:ΔFf为轧件与轧辊间的动态摩擦力。
ΔFf=2μ0ΔF+2ΔμF(0,0)+2ΔμΔF
(9)
联立轧件和轧辊2部分动力学方程可得轧机辊系振动方程:
(10)
4 实例分析与模型对比验证
以某厂1780板带轧机实际参数为例,对优化前后的模型进行数值解析,给定模型计算条件如表1所示。
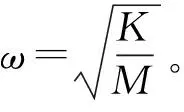

表1 板带轧机轧制参数
在实际轧制生产过程中,轧制速度对轧机辊系的振动起着重要作用,同时也是影响轧制效率的关键。为此,本文以表1所示的轧机参数为例,对式(10)所代表模型的轧件水平振动速度和轧辊垂直振动位移进行仿真,如图2和图3所示。
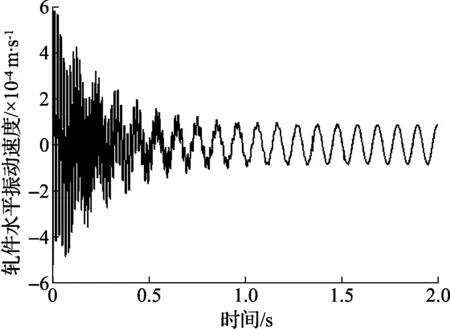
图2 轧件水平振动速度时间历程曲线
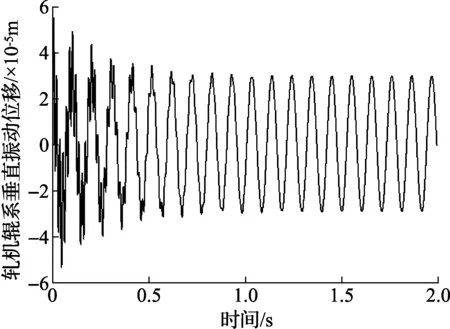
图3 轧机辊系垂直振动位移时间历程曲线
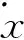
效性的基础。为了分析轧辊转速对轧件水平振动速度和轧机辊系垂直振动位移的影响,选取3组不同的轧辊转速进行仿真,只对系统处于稳定振动状态时进行分析,所得结果如图4和图5所示。
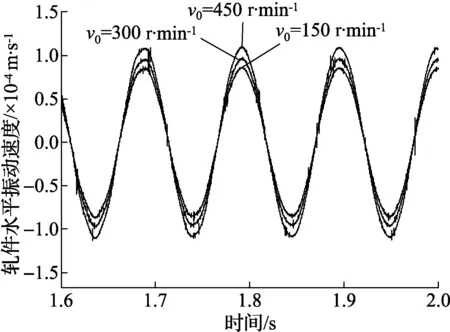
图4 不同轧辊转速下轧件水平振动曲线
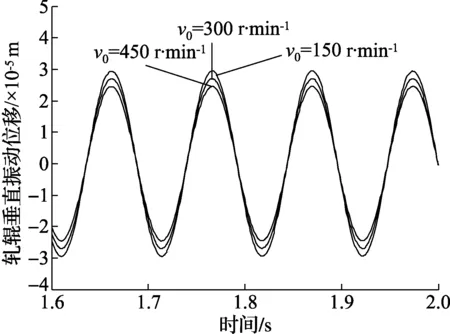
图5 不同轧辊转速下轧机辊系垂直振动曲线
从图4和图5所示的仿真结果可以看出,轧件水平振动速度随着轧辊转速的增大而增大,轧辊垂直振动位移的稳定幅值随着轧辊转速的增大逐渐减小。为了检验补偿前后模型的变化,现对1780轧机F1机架进行现场测试,为了避开系统瞬态误差,选取5组不同轧辊转速时的轧机系统进行测试,每组连续5次取样,每次间隔5 s。所得数据如表2所示。
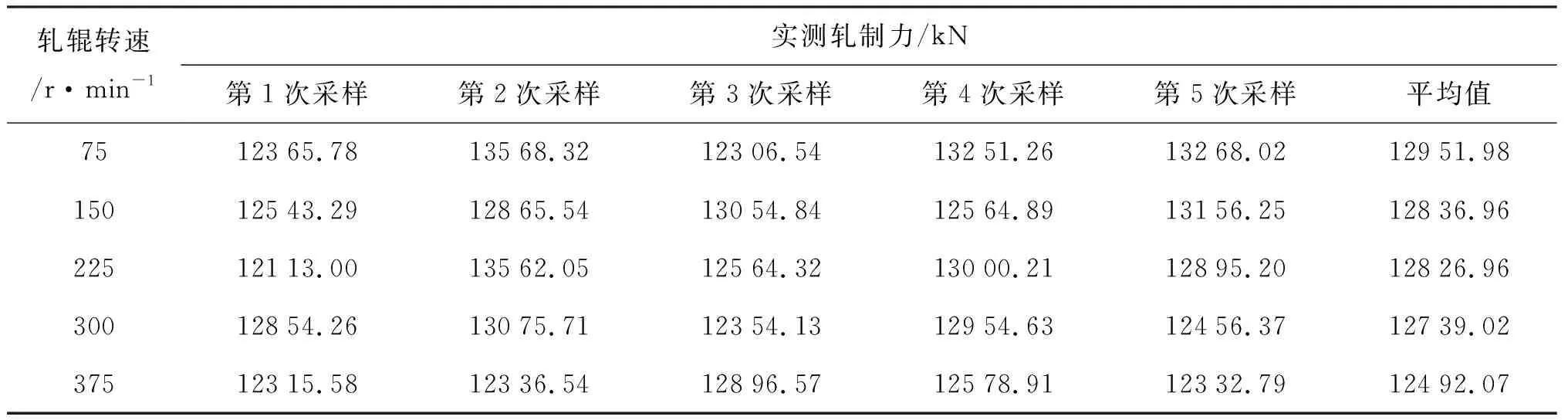
表2 轧制力现场测试数据
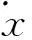
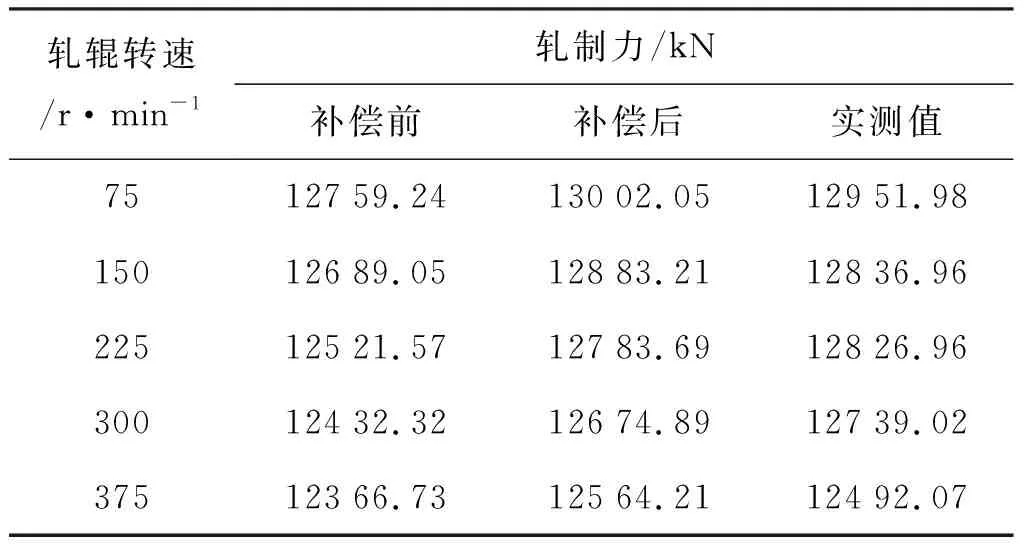
表3 模型补偿前后轧制力理论值与现场测试数据
从图6所示的仿真结果可见,轧件水平振动对轧机辊系振动模型的补偿,大大减小了轧制力计算值与实际测量值之间的误差。实验结果验证了轧件动力学补偿下的轧机振动模型的有效性,这对于轧制力预测和轧机振动分析有着重要的作用。
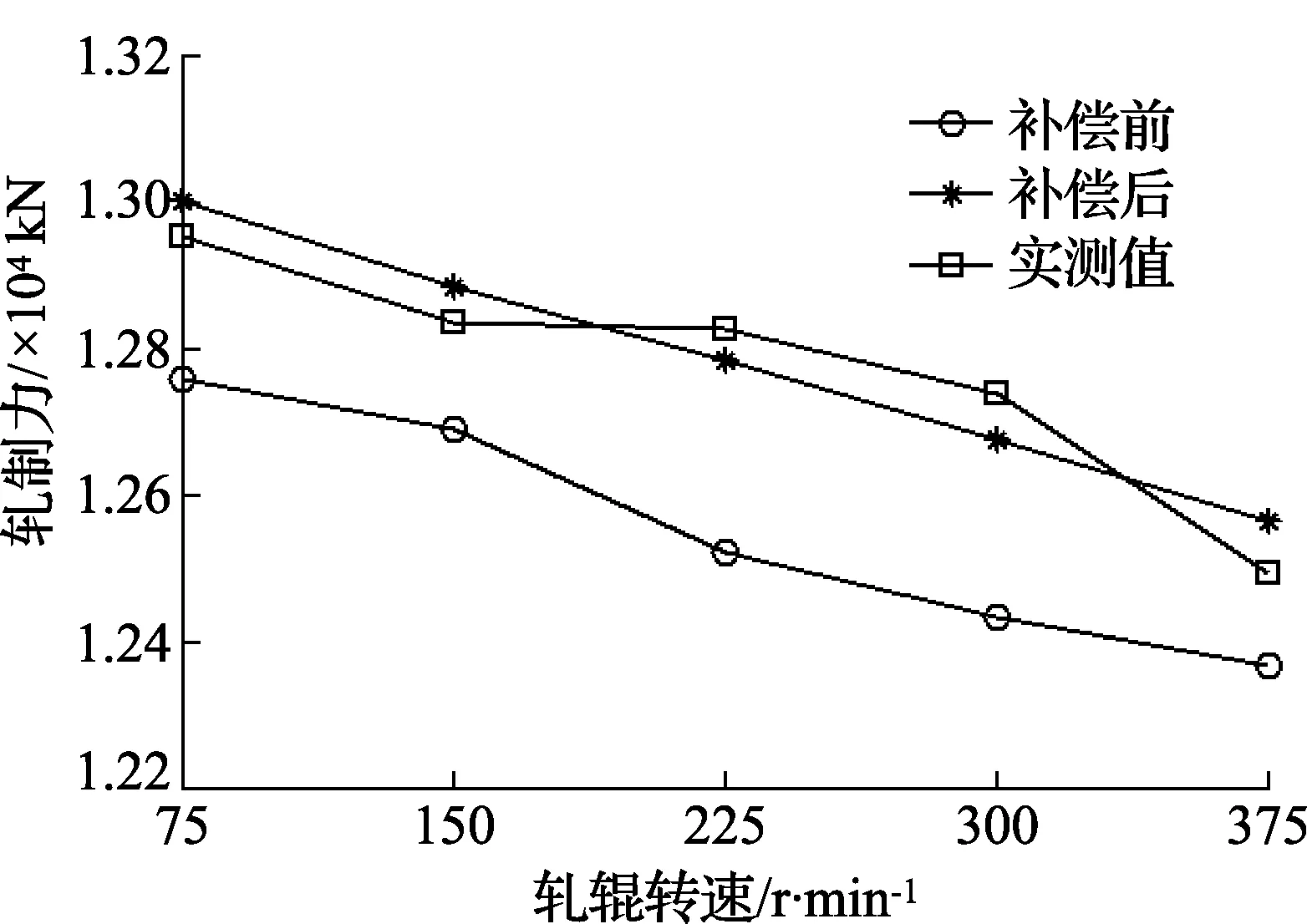
图6 不同情况下的轧制力仿真比较
5 结 论
(1) 在Hill轧制力计算公式的基础上,将轧制速度改进为轧辊转速和轧件水平振动速度和的形式,建立了一种轧件水平振动速度补偿的轧制力模型。在此基础上,考虑动态轧制力和动态摩擦力的非线性特性,建立了基于轧件水平振动的轧机辊系振动补偿模型。
(2) 在轧件水平振动的轧机辊系振动补偿模型基础上,通过改变轧辊转速,得到5组补偿前后轧制力理论值。通过与轧制力测试数据的对比,结果表明轧件水平振动补偿的轧机振动模型大大减小了轧制力理论值与测量值之间的误差,验证了补偿后轧机辊系振动模型的有效性,这对于轧制力预测和轧机振动分析有着重要的作用。
[参考文献]
[1] Brusa E, Lemma L. Numerical and experimental analysis of the dynamic effects in compact cluster mills for cold rolling[J].JournalofMaterialsProcessingTechnology, 2009, 209(5): 2436-2445.
[2] 刘彬, 蒋金水, 赵武, 等. 轧机转速波动测量的扭振监测实验研究[J]. 计量学报, 2007, 28(3):272-275.
[3] 谢长贵, 曾海. 1220冷连轧机带钢表面振纹机理的研究[J]. 计量学报, 2015, 36(6):595-598.
[4] Niziol J, Swiatoniowski A. Numerical analysis of the vertical vibrations of rolling mills and their negative effect on the sheet quality[J].JournalofMaterialsProcessingTechnology, 2005, 162/163(20):546-550.
[5] 范小彬, 臧勇, 王会刚. 热连轧机垂直振动特性研究[J]. 中国机械工程, 2010, 21(15):1801-1804.
[6] Liu F, Liu B, Liu H R,etal. Vertical vibration of strip mill with the piecewise nonlinear constraint arising from hydraulic cylinder[J].InternationalJournalofPrecisionEngineeringandManufacturing, 2015, 16(9):1891-1898.
[7] 王桥医, 黄海军, 李志华. 金属塑性加工工作界面非稳态润滑轧机振动控制[J]. 中南大学学报(自然科学版), 2010, 41(4):1418-1423.
[8] Yang X, Li Q, Tong C N,etal. Vertical vibration model for unsteady lubrication in rolls-strip interface of cold rolling mills[J].AdvancesinMechanicalEngineering, 2012, 4(12):1432-1437.
[9] 侯东晓, 朱月, 刘浩然, 等. 基于动态轧制力的冷轧机非线性振动特性研究[J]. 机械工程学报, 2013, 49(14):45-50.
[10] 邹家祥. 冷连轧机系统振动控制[M]. 北京:冶金工业出版社, 1998.

