中低速磁悬浮列车测速定位中的滤波方法研究

陈特放，曾铂洋，成 庶

（中南大学信息科学与工程学院，湖南长沙 410075）

0 引言

近年来，我国轨道交通行业发展迅速，磁悬浮已经成为一些城市轨道交通的建设热点之一，建设了诸如长沙黄花机场—长沙高铁南站等磁悬浮专线。由此可见，磁悬浮已经慢慢发展成为城市轨道交通的一种方式[1]。

对于中速磁悬浮（最高速度 120～200 km/h），目前由湖南省政府与国防科技大学联合成立的湖南省磁浮技术研究中心正在对 160 km/h 速度的中速磁浮进行研发；对于高速磁悬浮（最高速度在 200 km/h 以上），国家从“十五”规划开始，对高速磁浮的研发进行重点扶持，2010年4月，由国家磁浮中心进行总体设计，成都飞机公司制造了首节国产高速磁浮列车；对于超高速磁浮（最高速度在 500 km/h 以上），我国中车集团在国家重点研发计划的支持下，已着手进行超高速磁浮的关键技术研究。1934年，德国工程师赫尔曼 · 肯佩尔申请了磁悬浮的首次专利；1977年，德国已开发出各种类型的磁悬浮系统，并决定选择长定子驱动和电磁悬浮系统的技术路线（即后来上海高速磁浮采用的 Transrapid 系统）。日本 2005年开通世界首条中低速磁浮运营线路；2015年山梨试验线（超导高速磁浮）跑到速度 603 km/h，现正在修建速度 505 km/h 的高速磁浮中央新干线。韩国仁川机场中低速磁浮线 2016年开始在仁川机场至龙游车辆基地区间试运行，磁悬浮相关技术作为近年来的热门轨道交通研究内容引起了社会的广泛探讨[2-5]。

关于定位系统，目前国内外磁浮系统主要运用的定位系统是：①感应定子磁极测速，利用感应到的定子磁极信号源，速度低时，通过信号上升沿和下降沿测算速度，速度高时，通过计数接收脉冲测算速度；②感应编码器绝对定位，在轨道沿线间隔一定距离安装 1 个感应编码器，实现对列车的绝对定位，在 2 个感应编码器区间，则依靠累积感应长定子磁极测速的积分来实现相对定位[6-8]。

通过对各测速定位系统对比，拟采用北斗-惯导组合导航系统作为磁悬浮的测速定位系统，并进一步提出将自适应卡尔曼滤波应用于磁悬浮测速定位系统，以提高系统精度。

1 磁悬浮列车定位系统分析

目前在磁浮列车上使用的感应定子磁极测速和感应编码器这 2 种方法部件易磨耗，维护成本较高。实时速度与连续位置信号对于磁浮列车的牵引控制以及运行控制是极为重要的参数，但单一的速度和位置信号数据难以满足系统可靠性需求；另一方面，磁悬浮系统存在车轨距离加大、电磁耦合精度降低，且运行速度较快的问题，传统的轨道电路方法难以满足高精度测量要求。文献[9]提出利用脉宽编码式绝对定位器实现磁悬浮列车的绝对定位，优点在于磁浮列车绝对定位完全独立工作，不受外界因素干扰，能可靠、实时地获得列车位置信息，但这种方案修正误差值不够精准，达不到高精度要求。

在此基础上，提出采用组合导航系统进行定位测速，即北斗-惯导组合导航系统。组合导航具有高精度、高可靠性、高自动化性等优点。但是由于惯导系统的导航信息由积分过程获得，定位误差随时间增大，导致得到的结果不精准。如何减小误差获得更加准确的信息成为研究目标。

传统的减小误差的方法主要是使用递推法、最小二乘法，这些方法计算繁琐、不便仿真且精度不高。文献[10]、[11]提供了一种思路，可以考虑将卡尔曼滤波应用到磁悬浮列车定位系统上。但是，如何将卡尔曼滤波应用到磁悬浮列车测速定位系统上，以及如何将卡尔曼滤波算法进行优化达到高精度要求，或者结合其他优化方法达到提高精度的要求成为我们研究的主要方向。相对于传统方法，基于新息的自适应卡尔曼滤波便于使用且不受环境影响，便于仿真，且精度具有较大的提升[12-13]。本文将基于新息的自适应卡尔曼滤波引入中低速磁悬浮速度传感器，用于解决传入速度传感器的数据精度不够的问题，并进行实验仿真验证。

2 自适应卡尔曼滤波器设计

2.1 离散卡尔曼滤波模型

离散卡尔曼滤波状态空间模型有 2 个方程：

式（1）、（2）中：Xk为 N 维的状态向量；φk，k-1是系统n×n 维状态转移矩阵；Xk-1为 Xk上一时刻即 k-1 时刻的状态量；Ik，k-1是 n×p 维噪声输入矩阵；Wk-1是 p 维系统过程噪声；Zk是系统 m 维量测向量；Hk是 m×n 维量测矩阵；Vk是 m 维量测噪声；下标 k 表示第 k 时刻。

2.2 卡尔曼滤波算法

卡尔曼滤波是一种利用反馈控制的方法估计过程状态的滤波算法：滤波器估计过程某一时刻的状态，然后以（含噪声的）测量变量的方式获得反馈。卡尔曼滤波主要分为 2 个部分：时间更新方程和测量更新方程。其中，时间更新方程负责及时向前推算当前状态和误差协方差估计的值，以便于下一个时间状态构造和先验估计。测量更新方程负责反馈，即将先验估计和新的测量变量结合以构造改进后的后验估计。具体方程如下：

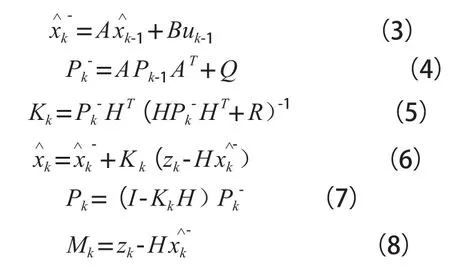
式（3）～（8）中：表示先验估计；A 为 n×n 阶增益矩阵；代表后验估计的上一时刻的状态量；B 代表控制函数 uk-1的 n×n 阶增益矩阵；为先验估计协方差；Pk-1为后验估计协方差 Pk的上一时刻的状态量；AT为 n×n 阶增益矩阵 A 的转置矩阵；Q 为过程激励噪声协方差；Kk表示滤波增益；HT代表H的转置矩阵；H 表示状态变量 xk对测量变量 zk的增益；R 代表量测噪声；I 代表单位矩阵；Mk为预报残差。

其中式（3）、（4）表示时间更新方程。式（5）、（6）、（7）表示测量更新方程。测量更新方程首先做的是计算卡尔曼滤波增益 Kk，然后测量输出以获得 zk，之后按照式（6）计算出后验估计，再按照式（7）计算后验估计协方差 Pk。计算完时间更新方程和测量更新方程，整个过程再重复。上一次计算得到的后验估计被作为下一次计算的先验估计，依次递推得到完整的数据。式（8）预报残差 Mk通常称为新息。

2.3 自适应卡尔曼滤波算法

磁悬浮列车在运行过程中，速度能否及时更新以及是否准确是考虑的重要因素之一。除了传感器的精度问题，对传回来的干扰信号进行处理也是提高精度的重要方法[14]。下面对磁悬浮列车运行速度进行模型搭建，并对在经典卡尔曼滤波与自适应卡尔曼滤波下不同处理进行对比。

通过对列车运行速度分析，以及现场采样，可以初步搭建出磁悬浮列车运行速度变化的模型与公式：

式（9）中，v 代表磁悬浮列车运行速度，km/h；t 代表1个周期内运行的时间，s。

由于经典卡尔曼算法的滤波效果主要依靠对参数值量测噪声 R 的实际方差的调整，然而，在列车运行过程中量测噪声的实际方差往往无法直接获得。本文提出思路，通过将自适应滤波与卡尔曼滤波结合解决该问题。通过对经典卡尔曼滤波分析可知，R 是受滤波增益Kk影响的，因此，可考虑通过调节 Kk来达到调节 R 的目的，从而调节量测噪声方差，达到自适应的目的。以新息方式列写卡尔曼滤波，设定变量，则可得如下公式：

代表Hk的转置矩阵；取长度为 k-M 的实测新息序列的滑动采样方差最优估计为：

式（14）中为预报残差，为预报残差的转置矩阵，为最优估计，文献[15]已证明为的极大似然估计值，且将式（14）代入式（11）可得新的增益方程：

该方法不需要提前得知量测噪声的先验知识，即不需要自己去调节参数，具有自适应性，通过计算最优估计，并将其引入经典卡尔曼滤波从而达到修正滤波增益的目的。该方法可以有效地解决不知道量测噪声而无法进行滤波计算的问题，且通过公式可知一定的自我校正性，可随系统进行迭代，实时进行协方差更新。下面通过实验仿真来验证其精准度与跟随性。

3 仿真模拟实验

首先通过搭建模型模拟无噪声干扰时的列车运行速度图线。

图1 中，红线代表无干扰时速度模型曲线。在模型中加入组合导航系统不规则干扰，得到如图2所示的曲线。

图1 初始无干扰磁悬浮速度曲线模型

图2 加入干扰后的磁悬浮速度曲线模型

图3、图4分别加入滤波算法，即分别为经典卡尔曼滤波算法（假定初始值）与自适应卡尔曼滤波算法，分别进行模型仿真。

图3、图4中灰线代表加入干扰之后的速度模型曲线，红线代表经过滤波算法后的滤波曲线。经过模拟对比可得出结论，自适应卡尔曼滤波效果与跟随性强于经典卡尔曼滤波，得知该方法应用于中低速磁悬浮速度传感器效果好于经典卡尔曼滤波。

图3 经典卡尔曼滤波中低速磁悬浮在运行中的速度变化模拟图

图4 自适应卡尔曼滤波中低速磁悬浮在运行中的速度变化模拟图

4 结束语

磁悬浮列车相关技术为新兴技术，成为研究热点。然而，因新采用的定位系统与之前采用的感应定子磁极等测速定位系统不同，故需研究新的方法应用于测速定位的滤波优化。

本文在深入分析自适应卡尔曼滤波的优点后，通过仿真对比经典卡尔曼滤波与自适应卡尔曼滤波。结论表明，自适应卡尔曼滤波具有有效的跟踪性、较强的适应性、更优的精准性，更适合应用于工程实践场合。

[1]邓小星. 中低速磁浮车辆系统动力学性能研究[D]. 四川成都：西南交通大学，2009.

[2]秦伟. 磁轮悬浮机构的电磁机理研究[D]. 北京：北京交通大学，2009.

[3]王博. 真空管道高温超导磁悬浮车气动特性研究[D]. 四川成都：西南交通大学，2017.

[4]赵海涛. 中低速磁悬浮列车制动系统性能研究[D]. 四川成都：西南交通大学，2017.

[5]贺光. EMS 型中速磁浮列车动力学建模与导向能力研究[D]. 北京：国防科学技术大学，2016.

[6]Zhihua Zhang, Liming Shi, Ke Wang,et al. Characteristics investigation of single-sided ironless pmlsm based on halbach array for medium-speed maglev train[J]. CES Transactions on Electrical Machines and Systems，2017，1（3）：375-382.

[7]毛保华，黄荣，贾顺平. 磁悬浮技术在中国的应用前景分析[J].交通运输系统工程与信息，2008，8（1）：29-39.

[8]Farhad Safaei, Amir Abolfazl Suratgar, Ahmad Afshar,et al. Characteristics optimization of the maglev train hybrid suspension system using genetic algorithm[J].IEEE Transactions on Energy Conversion，2015，30（3）：1163-1170.

[9]李晓龙，龙志强，刘曙生. 磁悬浮列车脉宽编码式绝对定位系统[J]. 传感器技术，2003，22（4）：57-59.

[10] 李江，王义伟，魏超，等. 卡尔曼滤波理论在电力系统中的应用综述[J]. 电力系统保护与控制，2014，42（6）：135-144.

[11] Rui Wang, Mingshan Liu, Yuan Zhou, et al. A deep belief networks adaptive Kalman filtering algorithm[C]//IEEE. 7th IEEE International Conference on Software Engineering and Service Science，2016：178-181.[12]辛英，于静. 自适应卡尔曼滤波算法改进与仿真[J].中国科技信息，2011（22）：59-60.

[13] Pravati Nayak, Jyoti Manjary Pattnaik, Sushmita Samantaray, et al. Comparative study of harmonics estimation in micro grid using adaptive extended Kalman filter[C]//IEEE. International Conference on Electrical, Electronics, and Optimization Techniques，2016：434-438.

[14] E. E. El Madbouly, A. E. Abdalla, Gh. M. El Banby.Fuzzy adaptive Kalman filter for multi-sensor system[C]//IEEE. International Conference on Networking and Media Convergence，2009：141-145.

[15]卞鸿巍，金志华，王俊璞，等. 组合导航系统新息自适应卡尔曼滤波算法[J]. 上海交通大学学报，2006，40（6）：1000-1003，1009.