基于有限元模拟的预压力式加筋土结构变形性能研究

江海龙，王少亭

(北京市建设工程质量第三检测所有限责任公司重庆分公司，重庆 401120)

0 引 言

法国工程师Heri·Vidal首先提出加筋土的概念，并修建了世界上第一座加筋土挡墙[1，2]。郑颖人等[3]通过对双排桩的研究得出了双排桩的受力模式和双排抗滑桩的排距在抗滑桩分别独立承受推力的时候是最合理的。介玉新等[4]对加筋土边坡研究试验认为加筋土边坡不会出现突然变形，边坡的破坏是先从内部开始，筋带的存在使得边坡的整体性能大幅提高。由于加筋土结构具有适应变形能力和抗震性，施工速度快，占地少，外形美观等特性，其在工程中的应用越来越广泛[5]。现阶段，对于加筋土结构的研究方法主要有模型实验和有限元模拟。在实际模型实验过程中，实验模型的建立受很多条件的约束，实验手段和实验条件也具有一定的局限性。在预压力式加筋土结构模型实验研究中，很多因素都会对实验结果有影响，实验过程中会有很多因素难以控制，对模型实验结果的准确性也会有一定的影响；而且模型实验或者现场实验经费较高，实验周期较长，能够模拟或者研究的工况也比较少，所以模型实验和现场实验都有很大的局限性。因此，有限元数值模拟方法在土木工程和其他的学科则发挥越来越重要的作用[6，7]。

数值分析的方法逐渐替代了一部分的模型实验和现场实验，在加筋土领域中数值模拟也给设计和科研提供了基础和依据。另外，随着加筋土结构的应用越来越广泛，加筋土结构的变形性能也越来越被工程师们所重视[8]，因此预压力式加筋土结构的变形性能分析至关重要。

本文利用有限元差分软件ANSYS[9，10]，通过建立有限元模型来模拟各种工况条件下的加筋土结构，探讨了施加于加筋土结构的预压力效果，研究了预压力对加筋土结构抗压、抗拉及变形性能的影响。

1 预应力加筋土基本原理

预应力加筋土强度增加的基本原理可以看作土体强度的增加是由于土体黏聚力增加造成的，与普通加筋土基本原理不同之处在于黏聚力增加的大小。普通加筋土所增加的黏聚力是由于加筋而增加的准黏聚力；对于预应力加筋土，其增加的黏聚力由两部分组成，由于加筋造成的准黏聚力和由于侧向应力增大造成的伪黏聚力。伪黏聚力是一种被动型黏聚力，因为只要存在这种侧向的压应力，伪黏聚力便会存在；而准黏聚力是一种被动型黏聚力，这种黏聚力的发挥是要借助于竖向荷载或竖向变形，没有竖向荷载或竖向变形加筋土便不存在准黏聚力的。预应力加筋土结构增加的黏聚力可以表示为下式：

C0=C′+Cp

(1)

式中：C0为预应力加筋土结构增加的黏聚力；Cp为预应力加筋土中由于加筋增加的准黏聚力；C′为预应力等效的黏聚力，即伪黏聚力。

2 计算模型的建立

本节数值模拟的计算模型主要由填料、土工织布、支压板，预压力构件四种单元组成，计算模型如图1所示，各项参数如表1和表2所示。

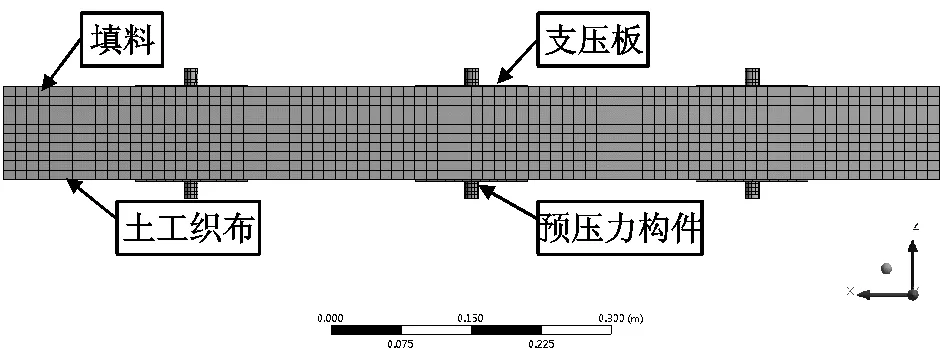
图1 有限元计算模型

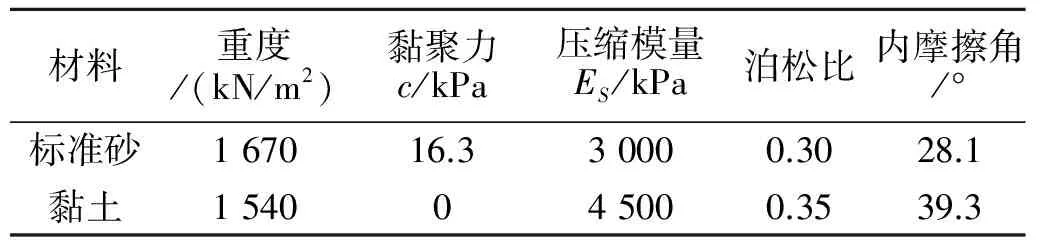
表1 土体的物理力学指标

表2 其他材料参数表

本节主要模拟不同的预压力、悬臂长度及不同填料对整体加筋土结构施加预压力的效果，各种条件如表3所示。

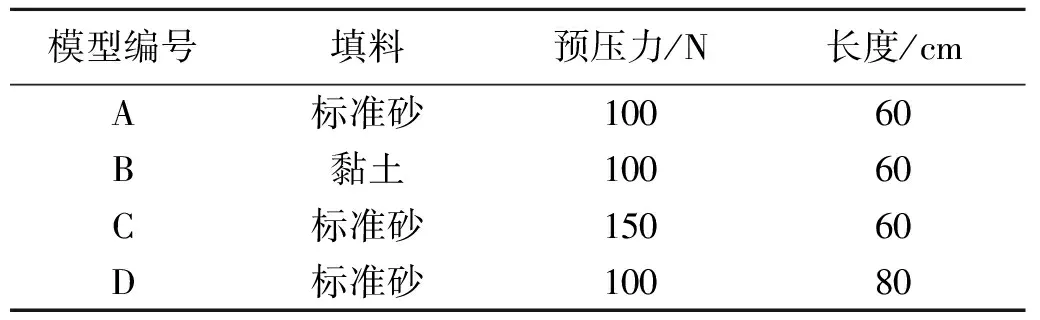
表3 计算模型参数表

3 结构施加预压力效果分析与评价

分别计算以下三种条件下预压力式加筋土结构的应力、变形的大小及分布情况，对比不同条件下结构的预压力施加效果。

3.1 不同填料下结构应力效果分析

图2(a)、(b)分别是填料为标准砂和黏土时计算模型结构中的应力分布云图。根据应力分布云图中的模拟结果分析得出，无论预压力式加筋土结构中使用哪种填土材料，应力分布的集中区域均为靠近支压板附近，两种填土材料下加筋土结构的应力分布范围大致相同。对于填料为标准砂的模型结构来说，其整体应力偏小，且各个部位上的应力大小基本相同，应力分布比较均匀。而相对于填料为黏土的模型结构来说，其整体应力分布在边界处偏小，在结构中部偏大，整体应力比填料为标准砂的模型结构大，计算得出填料为黏土时结构的整体应力提高了10%左右，说明在使用黏土材料作为填料时结构能够将所施加的预压力更大程度地扩散到结构中，从而在一定程度上增强了结构整体的应力水平。

3.2 不同预压力下结构应力效果分析

图3(a)、(b)分别为预压力100 N和150 N条件下计算模型整体应力分布云图。根据以上模拟结果分析得出，当增加预压力值时，模型的整体应力显著提高，计算得出其平均应力为0.75 MPa，对比提升了约25.6%。两种条件下其整体应力分布范围基本相同，对于预压力100 N模型结构来说其整体应力偏小，且各个部位上的应力分布比较均匀。预压力150 N结构的整体应力分布为边界处偏小，结构两侧与内部较大，根据结果可以得出增加预压力大小可以显著加强计算模型结构的应力水平。在两种预压力条件下，最大应力均发生在上支压板处，且位置相同；而最小应力均产生在边界上，位置相反。

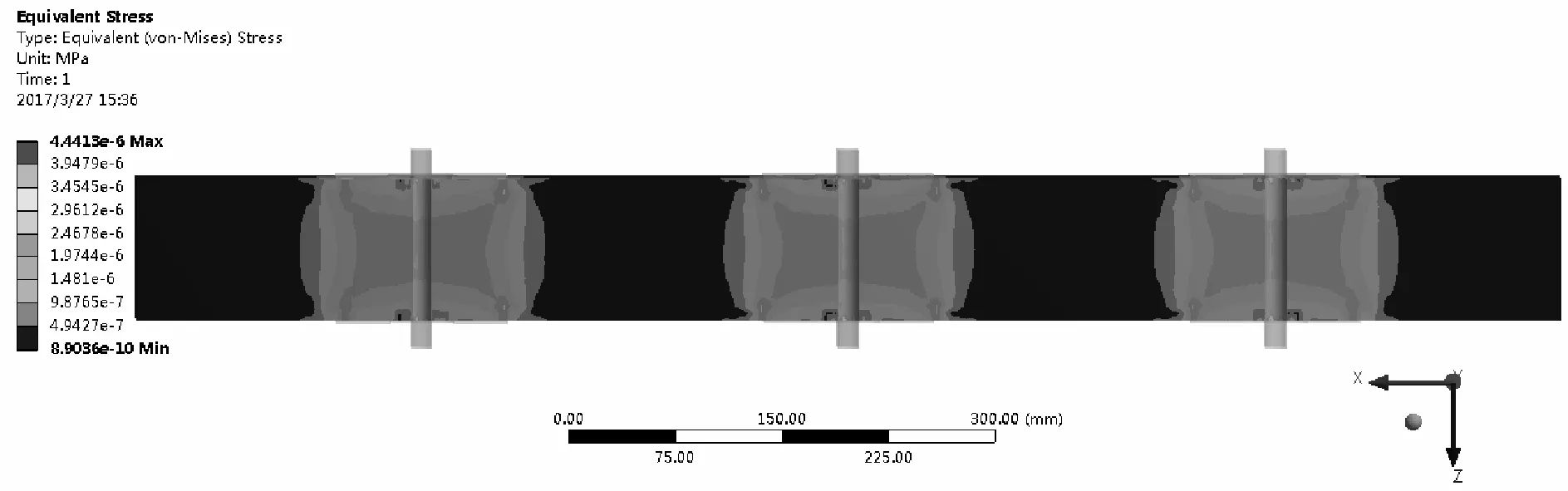
图2(a) 填料为标准砂时加筋土结构应力分布云图

图2(b) 填料为黏土时加筋土结构应力分布云图

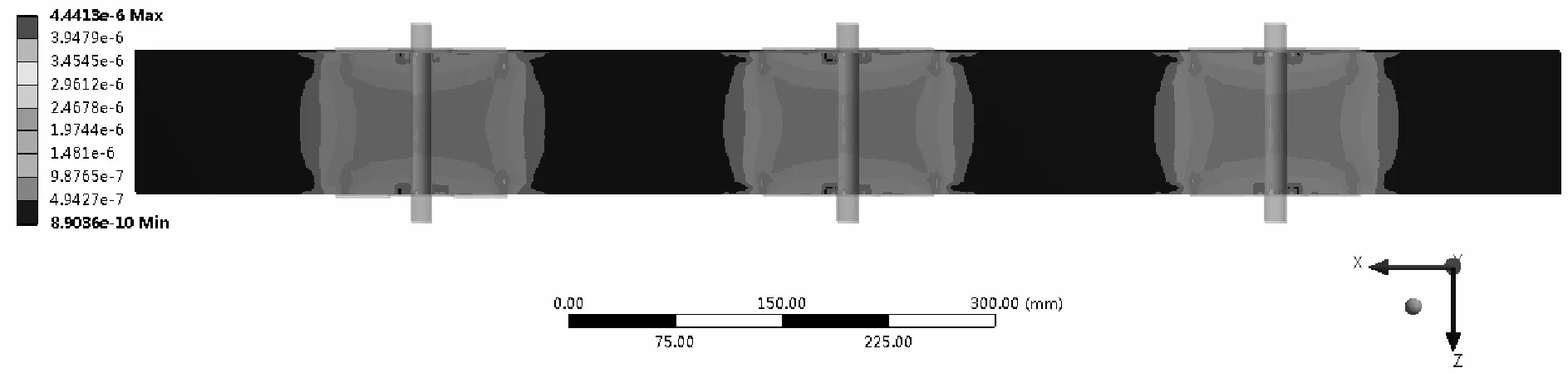
图3(a) 预压力为100 N时加筋土结构应力分布云图

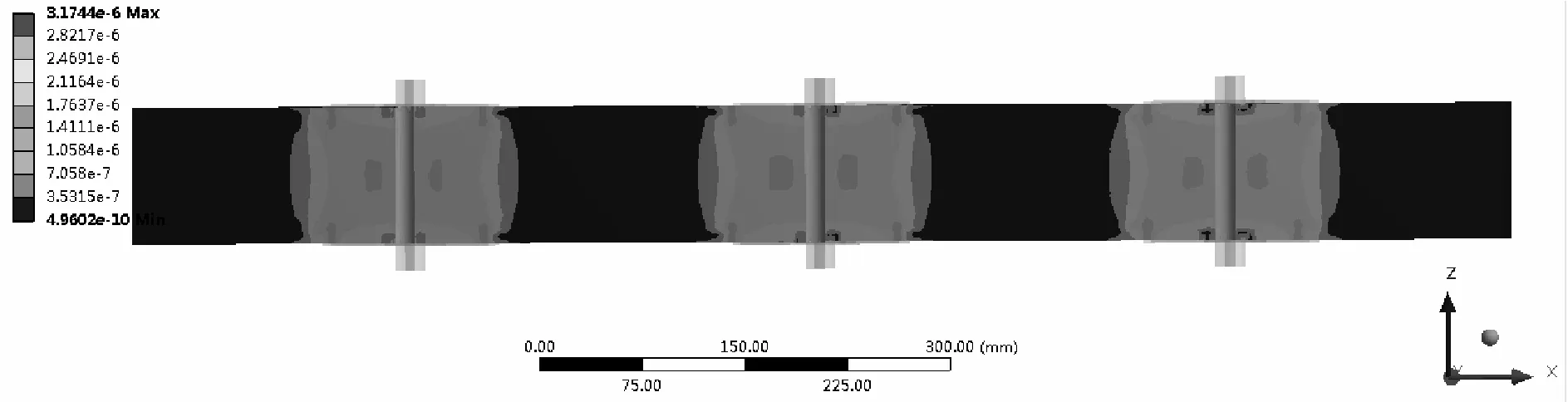
图3(b) 预压力为150 N时加筋土结构应力分布云图

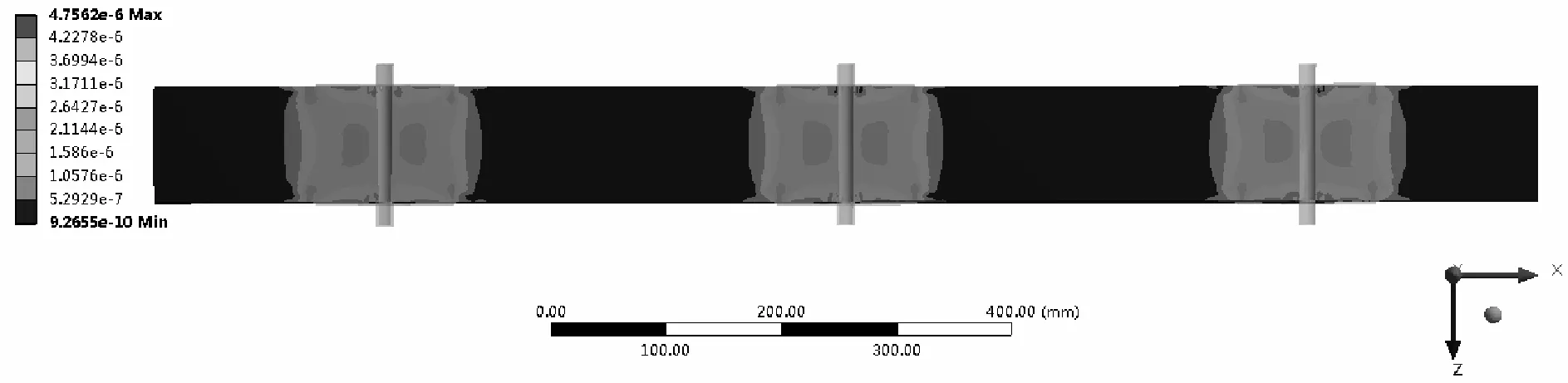
图4 (a)悬臂长度为100 cm时加筋土结构应力分布云图

3.3 不同悬臂长度下结构应力效果分析

图4(a)、(b)分别为悬臂长度100 cm和120 cm时计算模型整体应力分布云图。根据以上模拟结果分析得出，两种悬臂长度下应力整体分布规律基本相同。当悬臂长度为120 cm时，计算模型的整体应力主要集中在靠近支压板附近处，计算得出其平均应力为0.76 MPa，模型结构整体应力分布较紧凑且连续，分布较均匀。当悬臂长度为100 cm时，结构的整体应力分布规律为在支压板附近应力显著变大，而在结构上下表面的支压板间分布较小。

图4 (b)悬臂长度为120 cm时加筋土结构应力分布云图

4 结构施加预压力效果分析与评价

为了使计算结果具有一定的可靠性和准确性，本节数值计算模型采用二维实体单元。模型的尺寸设计为1.00 m×0.24 m×0.10 m和1.20 m×0.24 m×0.10 m(长×宽×高)两种规格。对于计算模型，其约束条件为模型底部(Z=0)平面边界采用固定约束，即约束底部(Z=0平面上)所有节点的X、Y二个方向的位移，模型边界约束条件如图5所示。分别计算预压力式加筋土结构在不均匀沉降下沉降变形的分布规律及大小，对比不同条件下结构的变形特征。

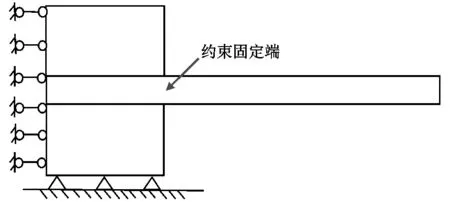
图5 模型边界约束条件示意图

4.1 填料为标准砂时加筋土结构的沉降情况

图6为采用标准砂作为填料的计算模型加筋土结构沉降变形分布云图。在数值模拟结果中可以看到，结构发生最大沉降处位于距悬臂固定端60 cm处，其最大沉降变形量为27.9 cm。

图6 填料为标准砂时结构沉降变形云图

4.2 填料为黏土时加筋土结构的沉降情况

图7为采用黏土作为填料的计算模型加筋土结构沉降变形分布云图。在数值模拟结果中可以看到，结构发生最大沉降处同样位于距悬臂固定端60 cm处，其最大沉降变形量为25.1 cm。

4.3 预压力为150N时加筋土结构的沉降情况

图8为采用150 N预压力得到的数值模拟加筋土结构沉降变形分布云图，在数值模拟结果中可以看到，结构最大沉降量依然发生在距悬臂固定端60 cm处，没有出现局部大变形，其最大沉降变形量为23.8 cm。

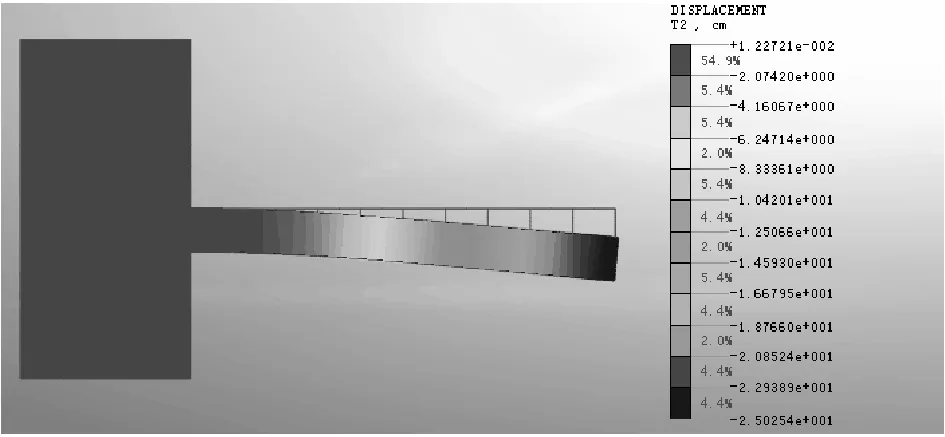
图7 填料为黏土时结构沉降变形云图

4.4 悬臂80 cm时加筋土结构的沉降情况

图9为悬臂长度为80 cm时数值模拟加筋土结构的沉降变形分布云图，在数值模拟结果中可以看到，尽管增加了结构的悬臂长度，但计算结果并没有出现局部大变形，其最大沉降变形量为30 cm。

图8 预压力为150 N时结构沉降变形云图

图9 悬臂长度为80 cm时结构沉降变形云图

5 结 论

a)在传统加筋土结构上施加预压力可改变土体内部应力分布状态。贯穿在土体内的受拉构件与结构上下表面支压板之间产生的预压力围压增强了土体的之间的摩擦作用，使得土体更加紧密，从而限制住了土体的侧向变形，增加了结构的整体强度。

b)模拟结果表明受拉构件起到在土体内部传递拉应力及使结构上下表面支压板产生预压力围压的作用，从而大大增加了结构的整体变形性能。

c)随着悬臂长度的减小，结构的整体应力分布规律为在支压板附近应力显著变大，在结构上下表面的支压板间变小。

参考文献：

[1] 陈从新，黄平路，卢增木.岩层倾角影响顺层岩石边坡变形性能的模型试验研究[J].岩土力学学报，2007，28(3)：476～481.

[2] 赵成刚.土力学的现状及其数值分析方法中某些问题的讨论[J].岩土力学，2006，27(8)：1361～1364.

[3] 唐芬，郑颖人，杨波.双排抗滑桩的推力分担及优化设计[J].岩石力学与工程学报，2010，31(6)：3162～3168.

[4] 介玉新，洛桑尼玛，郑瑞华，等.加筋土边坡的破坏形式[J].工程地质学报，2012，24(2)：693～699.

[5] 梁小勇，靳静，杨广庆.高速铁路土工格栅加筋土挡墙的试验研究[J].铁道建筑.2017，21(7)：108～111.

[6] 孙树林，时冬冬，秦鲜玮，等.库岸加筋土挡墙在地震和涌浪作用下的稳定性分析[J].科学技术与工程.2015，15(12)：0092～0097.

[7] 刘茂，杨红娟，吕建祥.刚性拉筋加筋土挡土墙内部滑移稳定性探索[J].中国地质灾害与防治学报.2016，27(3)：66～71.

[8] 祝晓寅，邓明文.浅析加筋土挡土墙变形性能[J].重庆交通学院学报，2003(S1)：77～79.

[9] 宿艳彩.基于ANSYS软件的桥架结构参数化有限元分析[D].西南交通大学，2006.

[10] 张智超，陈育民，刘汉龙，等.微型桩-加筋土挡墙路基结构的公路护栏抗冲击性能[J].中南大学学报(自然科学版).2017，48(8)：2169～2179.