基于云模型与证据理论的雷达导引头状态评估

逯 程，徐廷学，王 虹

(1.海军航空大学兵器科学与技术系,山东 烟台 264001； 2.中央军委联合参谋部第55研究所,北京 100094)

0 引言

随着装备结构日趋复杂，故障诊断及维修保障模式也面临新的挑战，视情维修(CBM)正逐步取代传统的定时维修，成为装备综合保障工作发展的新趋势[1]。装备的技术状态评估作为CBM的重要环节，能够为装备维修决策提供依据和支持，对于实现装备精确保障任务具有重要意义。

随着信息融合技术的发展，D-S证据理论在装备状态评估方面已经成功运用[2-3]。作为一种不确定性推理方法，20世纪60年代D-S证据理论[4]诞生于美国学者DEMPSTER在多值映射方面的工作，后由其学生SHAFER加以扩充和完善。相对于传统的概率理论，证据理论所定义的置信函数和似真函数，对信息的狭义不确定性等认知方面的表示、度量、处理都更为灵活，这就更加有利于描述来自不同渠道的不完整的模糊信息；同时，由于Dempster证据合成公式的引入，利用多源信息获得的估计结果也更加可靠。

现有的装备技术状态评估主要集中在层次分析法[5]、模糊集合理论[6-7]、人工神经网络[8]、隐Markov模型[9]、贝叶斯网络[10]等方法，而装备性能测试数据较少，存在各种不确定性问题，传统单一方法较难取得准确可信的评估结果。作为处理模糊性与随机性的有力工具，云理论[11]能够实现定性与定量信息的转换，为状态评估研究提供了一个新的思路。

基于以上分析，本文将云模型与D-S证据理论相结合，在隶属度赋值与证据源修正的基础上，通过D-S证据理论融合装备多个测试指标得到评估结果。雷达导引头状态评估实例验证了新方法的合理性。

1 D-S证据理论及云模型

1.1 D-S证据理论

定义1在专家系统中，设U为由一些有限的互不相容的元素组成的命题集合，则称U为识别框架,∅表示空的命题集合，若函数m∶2U→[0,1]满足

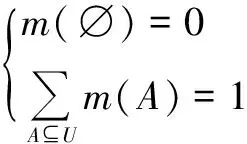
(1)

则称m(A)为A的基本可信度分配函数(BPA)，它表明对命题A的精确信任程度或对A的直接支持。若∀A⊆U，且满足m(A)>0，则称A为证据的焦元，所有焦元的并集称为核。

定义2设U为一个识别框架，m∶2U→[0,1]是U上的BPA，由

(2)

定义的函数Bel∶2U→[0,1]称为U上的信度函数。Bel(A)可以理解为证据对命题A的总支持度，由此可知，Bel(∅)=0，Bel(U)=1。

Dempster证据组合规则如下[12]：设Bel1和Bel2分别为识别框架U上的两个信度函数，m1和m2分别是其对应的BPA，焦元分别为A1,…,Ak，和B1,…,Br，则有

(3)

1.2 云模型

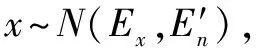
在正态云模型C(Ex,En,He)中，期望Ex反映了隶属度云的重心特征，熵En表示空间范围内可被接受的属性，超熵He则反映云滴的离散程度。因此，测试指标的云关联确定度求取算法如下：

2) 指标x与该云的关联度为

(4)

2 基于云模型与证据理论的状态评估方法

2.1 装备特征参数隶属度求取算法

本文针对某导引头4个关键测试参数c1,c2,c3和c4进行分析，将导引头分为良好、较好、堪用、拟故障和故障5个状态层级。具体参数数据如表1所示。

表1 原始数据及指标具体参数Table 1 Raw data and specific parameters

基于传统模糊理论的状态评估主观性太强，而云模型可以有效解决各评估指标因素随机性和模糊性的问题，还可以避免传统隶属函数构造过程中数据归一化所带来的信息损失。

在DST模型下，每个状态类的隶属度都假定为先前技术索引间隔的标准值Ex。云模型的分布根据先前技术指标和区间值的具体要求进行调整，其中，En=(cmax-cmin)/6。

2.2 基于灰靶贡献度的证据源修正算法

在整合过程中的证据理论将证据源同等对待，但不同的特征参数对状态等级的影响程度也有差异，一些较差的状态参数会影响综合设备的最终状态，因此有必要对于证据源进行融合前的修正调整。

基于灰靶理论[14]对证据源进行修正，将参数对标准靶心的贡献度与其重要程度相对应，具体步骤如下。

1) 根据各特征参数标准值确定标准模式υ0=(υ0(1),υ0(2),…,υ0(n))，υ0(n)为第n个特征参数的标准值。

2) 根据历史数据确定第k个参数序列υ(k)=(υ1(k),υ2(k),…,υm(k))，并进行统一测度变换

(5)

3) 计算参数k在差异信息空间中的灰关联系数

γ(xi(0),xi(k))=

(6)

式中，Δi(0,k)=|xi(0)-xi(k)|。

4) 计算参数k的贡献度，即参数k对装备状态的影响程度为

(7)

参数k的灰靶贡献度向量为

γ=(γ1,γ2,…,γn)。

(8)

5) 设γmax=max(γ1,γ2,…,γn)，αi=γi/γmax(i=1,2,…,n)为隶属度调整参数，则修正后的特征参数i证据源下各状态等级焦元的模糊隶属度为

(9)

式中，k=1,2,…,di，di为i证据源中非U焦元的个数。为满足定义2的条件，还需补充定义

(10)

2.3 状态评估流程

首先选择能够反映设备状态的特征参数，如果一个或多个参数超过阈值，则设备故障，需要立即安排相关技术人员进行设备维护，否则转移到退化状态的评估过程，分为良好、较好、堪用、拟故障4个等级[15]。

评估过程首先利用2.1节隶属度算法得到隶属度，然后利用2.2节方法对隶属度进行优化，最后在隶属度转化为BPA后，利用D-S证据融合得到最终结果。评估流程如图1所示。

图1 状态评估流程Fig.1 Flow chart of status evaluation

3 实例分析

根据某团7年的导引头开机检测数据记录进行仿真分析，期间导引头未发生故障现象，且最后一年的导弹雷达单元测试结果为合格状态，利用云模型与证据理论进行状态评估。

通过原始测试数据得到4个状态的云隶属度，如表2所示。

表2 各参数状态等级云隶属度Table 2 Cloud membership degree of parameter status class

进一步计算得到4个特征参数的隶属度调整系数分别为0.298,1,0.731和0.269，根据式(5)～(12)进行证据源修正，结果如表3所示。

表3 特征参数修正BPATable 3 Modified BPA of characteristic parameters

利用修正后的BPA进行证据融合，采用文献[16]中的合成公式进行计算，得到状态评估结果如表4所示。

表4 状态评估结果Table 4 Condition assessment results

本文利用正态云模型改进了传统的模糊隶属度的计算方式，客观性较强，而采用文献[17]的决策方法判定该导引头的最终状态为堪用状态。

进一步分析，由于导弹处于贮存状态，中间没有进行修理，性能状态应逐渐劣化，通过对前6年的导引头状态进行评估，结果分别为良好、良好、较好、较好、较好，符合实际情况，该纵向比较法[15]也验证了本文评估方法的合理性。

4 结束语

本文建立了基于云模型和证据理论的状态评估方法。首先，基于云模型计算特征参数的隶属度，然后根据特征参数的灰色目标贡献度对证据源进行修正，最后，将不同参数的BPA进行融合，得到评估结果。雷达导引头的评估算例验证了新方法是客观合理的，也为下一步的状态预测与维修决策奠定了基础。

参考文献

[1]BROWN E R,MCCOLLOM N N,MOORE E E,et al.Prognostics and health management a data-driven approach to supporting the F-35 Lightning II[C]//Aerospace Conference,IEEE,2007:1-12.

[2]LIAO J,BI Y,NUGENT C.Using the Dempster-Shafer theory of evidence with a revised lattice structure for activity recognition[J].IEEE Transactions on Information Technology in Biomedicine,2011,15(1):74-82.

[3] 高峰,唐卓贞.基于DS证据理论的船舶电子设备状态预测方法[J].船电技术,2011,31(2):45-48.

[4]SMARANDACHE F,DEZERT J.Applications and advances of DSmT for information fusion[J].Instrument Standardization & Metrology,2006,368(2):417.

[5] 于文武,许春生,康力平.基于AHP的航空发动机健康评估系统设计[J].航空计算技术,2007,37(1):73-74.

[6] AMMAR S,DUNCOMBE W,JUMP B,et al.Constructing a fuzzy-knowledge-based-system:an application for assessing the financial condition of public schools[J].Expert Systems with Applications,2004,27(3):349-364.

[7] KAWAMURA K,MIYAMOTO A.Condition state evaluation of existing reinforced concrete bridges using neuro-fuzzy hybrid system[J].Computers & Structures,2003,81(18):1931-1940.

[8]AZADI M,POURAKBAR S,KASHFI A.Assessment of optimum settlement of structure adjacent urban tunnel by using neural network methods[J].Tunnelling and Underground Space Technology,2013,37:1-9.

[9]PENG Y,DONG M.A prognosis method using age-dependent hidden semi-Markov model for equipment health prediction[J].Mechanical Systems and Signal Processing,2011,25(1):237-252.

[10] JIN G,MATTHEWS D E,ZHOU Z.A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries in spacecraft[J].Reliability Engineering & System Safety,2013,113:7-20.

[11] 李德毅,刘常昱.论正态云模型的普适性[J].中国工程科学,2004,6(8):28-34.

[12] 苏晓燕.关联证据融合研究[D].上海:上海交通大学,2014.

[13] WANG G,XU C,LI D.Generic normal cloud model[J].Information Sciences,2014,280:1-15.

[14] 邓聚龙.灰理论基础[M].武汉：华中科技大学出版社,2002：172-195.

[15] 姚云峰,伍逸夫,冯玉光,等.装备健康状态评估方法研究[J].现代防御技术,2012,40(5):156-161.

[16] 张仕新,昝翔,李浩.基于云重心评估法和熵值法的装备技术状态评估[J].计算机测量与控制,2014,22(12):4015-4018.

[17] 丛林虎,徐廷学,董琪,等.基于改进证据理论的导弹状态评价方法[J].科技导报,2013,31(30):15-18.