分式考点大盘点之一:分式计算
曹玲玲
分式是有别于整式的另一类重要代数式,也是中考的必考内容,通常以填空题、选择题、解答题的形式出现.为帮助同学们及时了解分式在中考中的重要地位,现列举2017年的中考考题和同学们一起赏析.
考点1:分式的定义
【例1】(2017·贺州)下列各式中是分式的是( ).
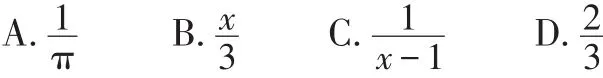
【分析】根据分式的概念进行正确选择.
【解】对照分式定义,选项C中的代数式符合要求,故选C.
【点评】在判断一个式子是不是分式时,出题者常将π放在分母上设置陷阱.同学们一定要注意,π是常数,不是字母!
考点2:分式的意义
A.x>3 B.x=3 C.x<3 D.x≠3
【分析】要使一个分式在实数范围内有意义,必须满足“分母不为零”.
【解】依题意得,x-3≠0,解得x≠3,故选D.
【点评】要使分式有意义,即要求分母不为零.
考点3:分式的值为零的条件
【例3】(2017·淄博)要使分式的值为零,则x的值是( ).
A.1 B.-1 C.±1 D.2
【分析】分子为零且分母不能为零,分式的值为零.据此求解.
【解】依题意得:| x|-1=0且x+1≠0,解得x=1,故选A.
【点评】对这类问题,同学们往往只会想到分子为零,而忽视“分母不能为零”的条件.此类题目还提醒我们,如果做出的答案有多解,一定要检验这些解是否都满足题意.
考点4:分式的基本性质

(1)该同学解答过程是从第 步开始出错的,其错误原因是 ;
(2)请写出此题正确的解答过程.
【分析】根据分式的运算法则即可求出答案.
【解】(1)一;分式的基本性质用错;
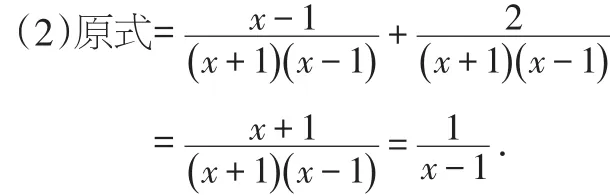
【点评】异分母的分式相加、减,需要先通分,再加、减.通分时一定要注意分子、分母要同时乘一个数或者式子,这样才能保证分式的值不变.同学们最容易犯题目中出现的错误——分子漏乘.
考点5:分式的约分

【分析】约分时,分子与分母都必须是乘积式,如果是多项式,必须先分解因式.
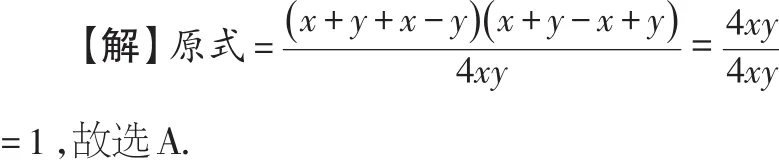
【点评】本题需要同学们能够灵活运用因式分解的相关知识和分解技巧,将(x+y)和(x-y)看作整体进行因式分解.
考点6:最简公分母
【例6】(2017·桂林)分式与的最简公分母是 .
【分析】确定最简公分母的方法是:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的.这样得到的因式的积就是最简公分母.
【解】两个分式的分母分别是2a2b、ab2,故最简公分母是2a2b2.答案是2a2b2:
【点评】确定分式的最简公分母是对分式进行通分的第一步,而“分式通分”常常又是异分母分式相加、减的必经过程,所以确定分式的最简公分母是基础,也很重要.
考点7:分式的混合运算

【分析】根据分式的运算法则,按照运算顺序进行运算即可.
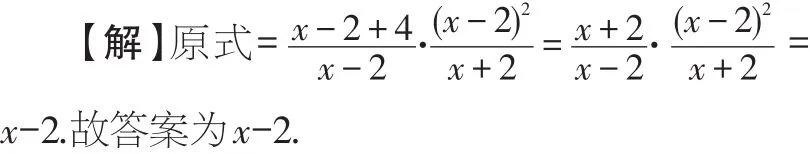
【点评】对于此类题目,同学们不仅要熟练掌握分式混合运算的顺序和法则,计算时还要非常细致谨慎.注意运算结果一定要化为最简分式或者整式.
考点8:分式的化简求值

【分析】将原式括号中两项通分并利用同分母分式的减法法则计算,约分得到最简结果,把x的值代入计算即可.

【点评】此题告诉我们,对分式进行化简时,不仅要熟练掌握分式混合运算的顺序和法则,还要注意选用简便的方法.本题则利用整体思想,将x+2看作一个整体进行通分,大大简化了运算过程.
考点9:分式开放题
见本期《自选数值有文章 取值范围记心上》一文.

