基于Simulink的水下无人机器人建模与仿真
, ,
(1.上海大学 机电工程与自动化学院,上海 200072;2.欧舶智能科技(上海)有限公司,上海 200436)
近年来,随着人类对海洋资源的进一步开发利用,适用于长时间、大范围水下作业的无人操作运载体(也称水下无人机器人(ROV))在军事及民用领域发展迅猛。根据与水面支持设备(母船或平台)间的联系方式,可以将水下无人机器人分为两大类:一类是有缆水下无人机器人,即水下遥控运载体,由母船通过电缆向ROV提供动力,人在母船上通过电缆对ROV进行遥控;另一类是无缆水下无人机器人,即水下自主式无人运载体 (AUV),它自带能源,依靠自治能力来管理和控制自己,以完成人赋予的使命。有缆水下无人机器人按运动方式可分为拖曳式、(海底)移动式和浮游(白航)式等3种。无缆水下无人机器人只能是自治式的,按规划的航线执行任务。
水下无人机器人运动学理论方程包括平动方程和转动方程,是根据动量定理和动量矩定理推导出的[1-2]。然而,水下无人机器人运动学理论方程不便于在控制和仿真中进行应用,主要原因是[3]:第一,采用向量叉乘形式,不便于方程展开和变换;第二,方程不是规范形式,必须经过繁琐的推导后才能用于实际的控制和仿真运算;第三,控制量的表达形式既不统一也不规范。
Matlab软件下的Simulink平台是一种有效的可视化仿真环境[4],可以快速、准确地建立动态系统的框图模型。设计的控制算法被应用后,仿真结果可以用Simulink的示波器以图像的形式显示出来,同时可将数据保存到Matlab工作空间中以便进一步分析。Simulink平台进行仿真的优点是:框图搭建方便,仿真可以随时修改,编程完全可视化。
本文基于Simulink平台对水下无人机器人进行建模与仿真,仿真模型是根据水下无人机器人运动学模型建立的,可适用于多种类型的水下无人机器人。
1 水下无人机器人的运动学模型
水下无人机器人的运动学模型[5-6]如图1所示。该模型具有六自由度运动坐标系,X轴为艇艏方向,Y轴为横轴,Z轴为垂直轴,φ为绕X轴转动的横滚角、θ为绕Y轴转动的俯仰角,ψ为绕Z轴转动的偏航角。
基于水下无人机器人机体坐标系的六自由度扩展坐标为
η=xyzφθψT
(1)
式中:x、y、z为机体的空间坐标。

图1 六自由度坐标系Fig.1 Six degrees of freedom coordinate
基于地理坐标系的六自由度扩展坐标为
η0=x0y0z0φ0θ0ψ0T
(2)
由于水下无人机器人的自身传感器读到的数据为机体坐标系下的姿态数据,因此需要通过欧拉角转换方法才能得到地理坐标系下的姿态数据。六自由度的欧拉角转换可以描述为
(3)
对于ROV系统,通过对其受力进行分析,可得到其六自由度空间运动方程为[7]

(4)
式中:v为ROV的速度向量;M为ROV的质量矩阵;C为科氏力和向心力矩阵;D为水动力阻尼矩阵;g(η)为重力和浮力产生的力或力矩向量;τ为推进系统产生的力或力矩向量。
2 Simulink模型的建立
由上述水下无人机器人的一般模型可以得到简化参数M、C、D和g(η)。设τ为推进系统产生的力或力矩向量,有
τ=LT1T2…TnT
(5)
式中:L为系数,由水下无人机器人的各个螺旋桨推进器到重心的距离来确定;Tn为第n个推进器的推力[7]。式(4)的运动学模型经过转换可以得到

(6)
方程(6)在Simulink环境中的实现如图2所示。
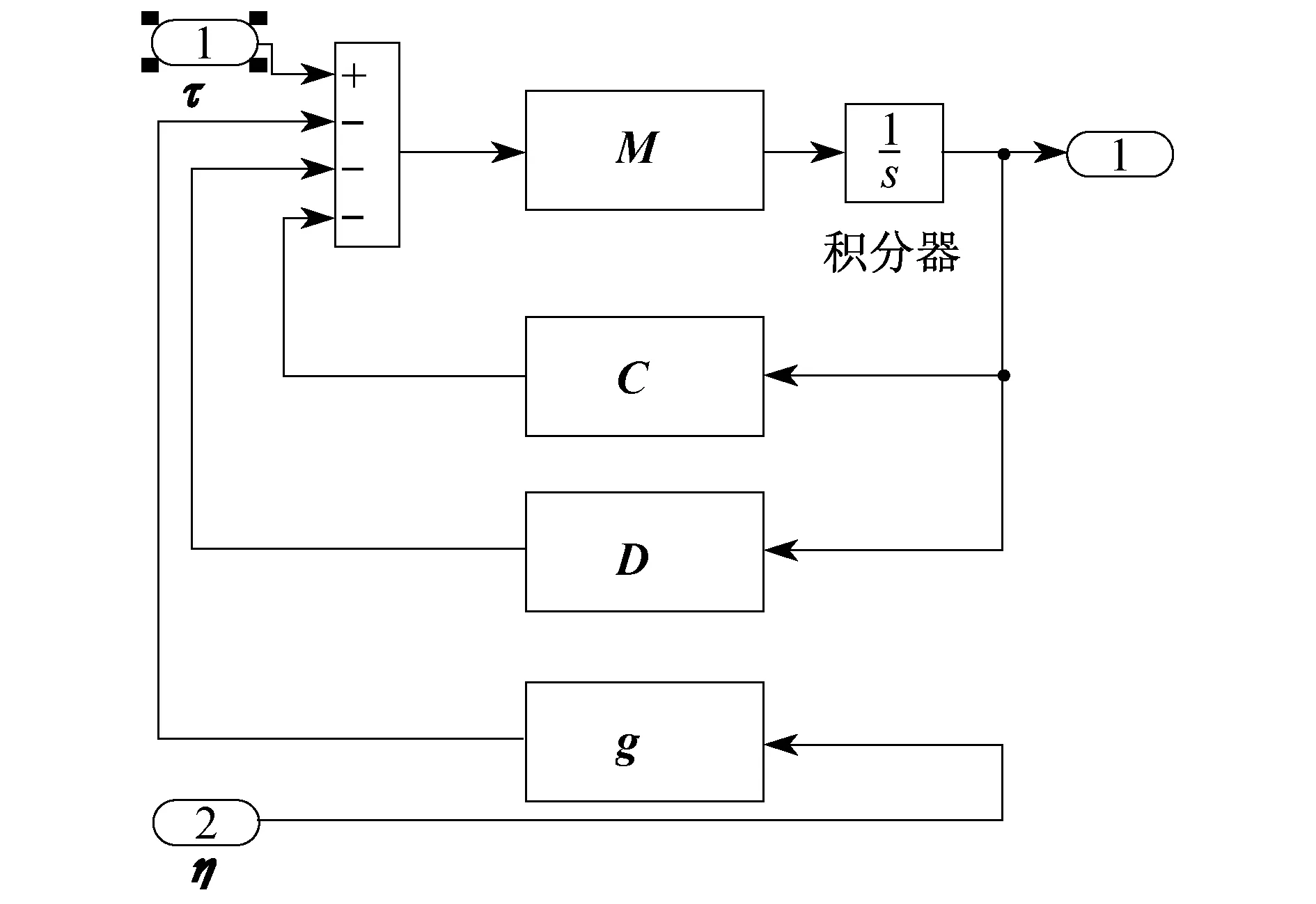
图2 ROV的Simulink模型Fig.2 Simulink model of ROV
科氏力和向心力矩阵C的计算结构如图3所示。图3中,K为乘系数,u为模块输入值。
ROV在水中的阻力由D得到,如图4所示。
ROV的重力W和浮力B由g(η)得到,如图5所示。图5中,xg、yg、zg为重心的空间坐标,xb、yb、zb为浮心的空间坐标。

图3 ROV的科氏力和向心力Fig.3 Coriolis force and centripetal force of ROV

图4 ROV在水中的阻力Fig.4 Resistance of ROV in the water

图5 ROV的重力和浮力Fig.5 Gravity and buoyancy of ROV
3 控制器设计及Simulink仿真
由于水动力系数的复杂性和涌流环境的多变性,很难得到精确的系统模型。滑模控制的优点是能够克服系统的不确定性,对干扰和未建模动态具有很强的鲁棒性,尤其是对非线性系统具有良好的控制效果[8-11]。本文设计的滑模控制器如图6所示,系统的仿真周期为0.1 s。根据水下无人机器人系统的期望动态特性设计系统切换超平面,如下所示:
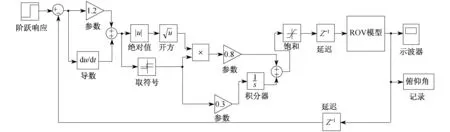
图6 滑模控制器的Simulink仿真图Fig.6 Simulink simulation diagram of sliding controller
(7)
式中:σ为滑模面;P为调节参数;θ和θy分别表示俯仰角的测量值与设定值;e为测量值与设定值的差值。滑模控制方程为
(8)
式中:F0为调节参数。通过调节F0和K来满足到达条件,从而使趋近运动(非滑动模态)在有限时间内到达切换面。
以俯仰角的控制为例,将水下无人机器人的俯仰角手动拨到25°,放开后机器自身回到平衡点。实际俯仰角响应曲线如图7所示。

图7 ROV俯仰角从25°到平衡位置Fig.7 Pitch angle of ROV from 25° to equilibrium position
在Simulink环境搭建的模型中,给模型一个短时间的脉冲量,可以得到所建模型俯仰角的变化。调节系统参数使得所建模型俯仰角响应曲线与ROV实际俯仰角响应曲线更接近。模型的俯仰角响应曲线如图8所示。

图8 ROV模型俯仰角从35°到平衡位置Fig.8 Pitch angle of ROV model from 35° to equilibrium position
在Simulink环境下设计滑模控制器。调节控制算法中的比例-积分-微分(PID)参数为:Kp=1.2,Ki=0.8,Kd=0.3。将水下无人机器人俯仰角设定为30°,则可得到俯仰角变化轨迹,如图9所示。从图9看出,所设定参数符合水下无人机器人控制需求。通过该控制算法得到的响应速度高,在0.6 s就进入稳定状态,并且稳态振幅小(±1°)。
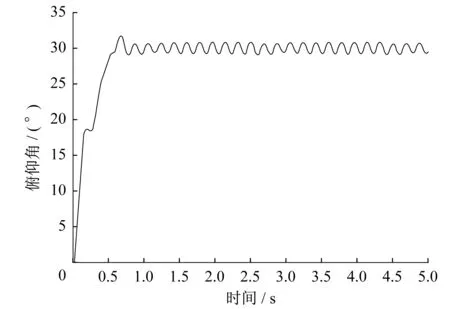
图9 Simulink环境下ROV俯仰角变化轨迹Fig.9 Trajectory of ROV pitch angle in Simulink environment
以该组控制参数为参考,进行真实的水下无人机器人的滑模控制器参数调节。取Kp=1.50,Ki=0.93,Kd=0.26,将俯仰角设定为30°,得到的响应曲线如图10所示。水下无人机器人在0.5 s就进入稳定状态,稳态振幅范围为27°~35°。一般静止水环境下参数调节的稳态振幅范围目标是±5°,因此该组控制参数下真实机器人的表现非常理想。
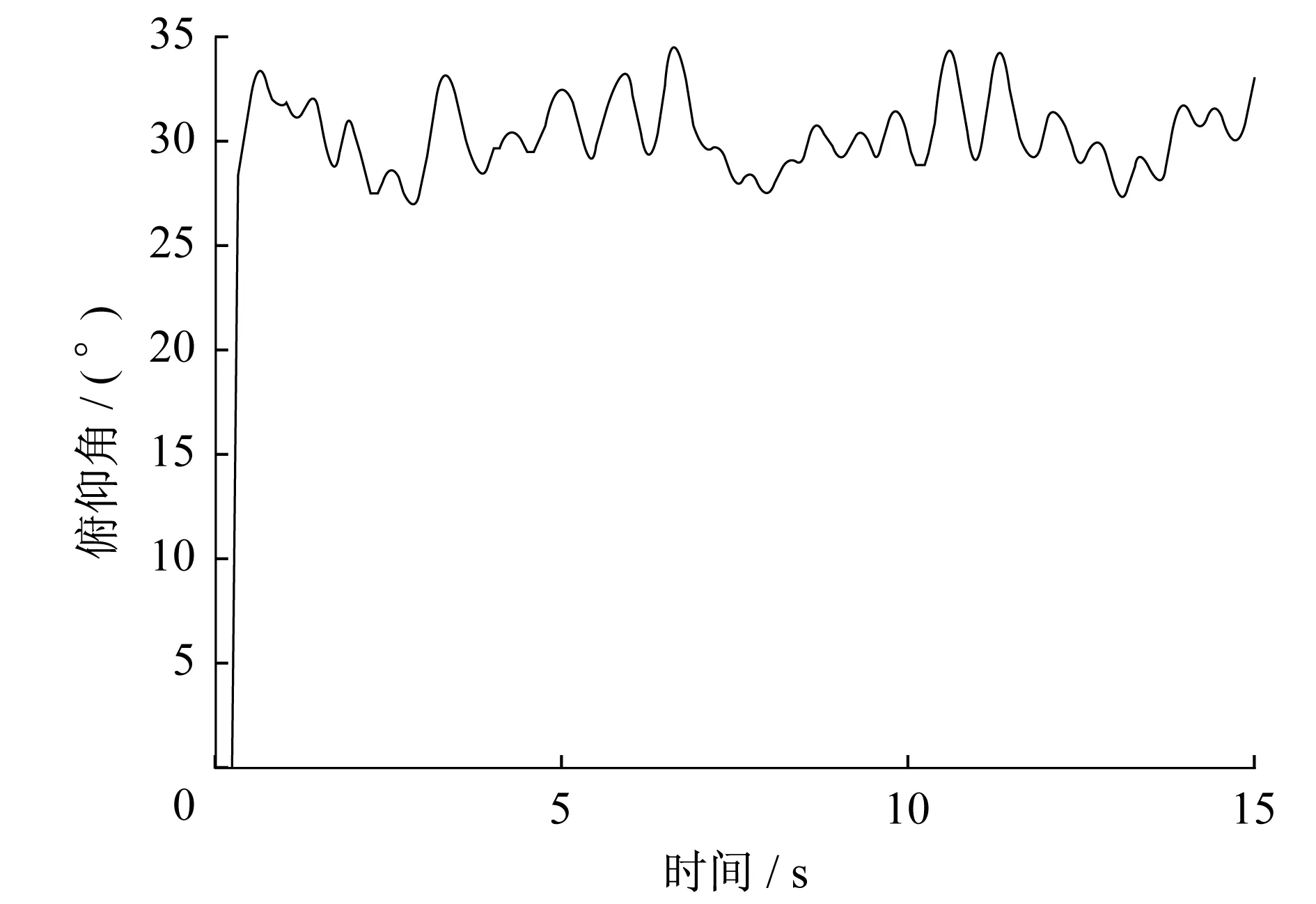
图10 ROV俯仰角变化轨迹Fig.10 Trajectory of ROV pitch angle
4 结语
本文探讨了Simulink环境下水下无人机器人的建模问题,通过设计滑模控制算法对ROV俯仰角进行控制。仿真与实验结果表明,实际与仿真环境下的最优控制参数比较接近,表明该Simulink仿真模型对实际系统控制参数的调节具有很高的参考价值。
参考文献:
[1] VALAVANIS K P,GRACANIN D,MATIJASEVIC M,et al.Control architectures for autonomous underwater vehicles[J].IEEE Control Systems,1997,17(6):48-64.
[2] 戴学丰,边信黔.6自由度水下机器人转变控制仿真研究[J].系统仿真学报,2001,13(3):368-369.
DAI Xuefeng,BIAN Xinqian.Simulation on trajectory control of a 6-DOF underwater vehicle[J].Journal of System Simulation,2001,13(3):368-369.
[3] 常文君,刘建成,于华南,等.水下机器人运动控制与仿真的数学模型[J].船舶工程,2002(3):58-60.
CHANG Wenjun,LIU Jiancheng,YU Huanan,et al.A mathematical model for motion control and simulation of underwater vehicle[J].Ship Engineering,2002(3):58-60.
[4] 郭训华,邵世煌.Simulink建模与仿真系统设计方法及应用[J].计算机工程,2005,31(22):127-129.
GUO Xunhua,SHAO Shihuang.Design of Simulink modeling and simulation and its application [J].Computer Engineering,2005,31(22):127-129.
[5] FOSSEN T I.Guidance and control of ocean vehicles[M].New York:Wiley,1994.
[6] 陈洪海,李一平.自治水下机器人全自由度仿真[J].控制工程,2002,9(6):72-74.
CHEN Honghai,LI Yiping.Simulation of AUV in six degrees of freedom[J].Control Engineering of China,2002,9(6):72-74.
[7] 朱康武.作业型ROV多变量位姿鲁棒控制方法研究[D].杭州:浙江大学,2012.
ZHU Kangwu.Research on multivariable robust position and attitude control of work-class ROV[D].Hangzhou:Zhejiang University,2012.
[8] PERRUQUETTI W J P.Sliding mode control in engineering[M].New York:Dekker,2002.
[9] YUH J.Modeling and control of underwater robotic vehicles[J].IEEE Transactions on Systems,Man,and Cybernetics,1990,20(6):1475-1483.
[10] 穆效江,陈阳舟.滑模变结构控制理论研究综述[J].控制工程,2007(增2):1-5.
MU Xiaojiang,CHEN Yangzhou.Overview of sliding mode variable structure control[J].Control Engineering of China,2007(S2):1-5.
[11] 王祝炯.滑模变结构控制系统设计方法研究[D].杭州:浙江工业大学,2003.
WANG Zhujiong.Design method study of sliding mode variable structure control system[D].Hangzhou:Zhejiang University of Technology,2003.

