基于并行差分进化算法的相量测量单元优化配置
, ,
(同济大学 电子与信息工程学院,上海 201804)
PMU优化配置(OPP)问题是一个非确定性多项式(NP)问题,需要寻找一个有效且高效的算法。文献[2]中提出了基于免疫二值粒子群算法的OPP,将安装的PMU个数和不可观测的节点数作为适应度函数,并使PMU个数最少。文献[3]中使用非支配排序遗传算法解决OPP问题,对所有的节点都根据支配和非支配关系进行分层排序,同一层节点指定同一个虚拟适应度,保证了同一层节点个体有相同的复制概率。文献[4]中提出了利用免疫遗传算法来解决OPP问题,并分析了电力系统中任意一个设备出现故障时的观测情况。文献[5]中使用二进制遗传算法对PMU进行优化配置,考虑了传统电流测量,在PMU配置确定的基础上最小化电流相量测量数。文献[6]中研究了基于禁忌算法的OPP,同时考虑了电力系统的完全可观测性和最大冗余度。文献[7-9]中分析了基于整数线性规划的系统可观测性。
差分进化(DE)算法由于其强大的全局优化能力引起了学术界的广泛关注。1995年Storn等[10]首次提出了一种简单、有效的DE算法。DE算法在OPP问题中也得到了应用。文献[11]中考虑了电力系统完全可观测的情况下DE算法在OPP问题中应用的有效性和准确性。文献[12]中针对给定系统利用DE算法的5种变异策略实现OPP,使完全可观测PMU数目达到最小。文献[13]中讨论了不考虑系统零注入节点和考虑系统零注入节点2种情况下,DE算法在OPP问题中的应用。
为了进一步提高DE算法的准确性,本文提出使用并行差分进化(PDE)算法解决基于全局可观测的OPP问题。
1 基于全局可观测的OPP问题模型
1.1 OPP问题的优化目标
对于一个具有n个节点的电力系统,根据给定的拓扑结构,系统OPP问题的优化目标是在满足一定约束条件下,使得下式成立:
(1)
式中:f(x)为目标函数,表示电力系统配置PMU最佳方案时耗费的总价;n为给定的母线节点数,如果节点i上安装了PMU,则xi=1(i=1,2,…,n),否则xi=0(i=1,2,…,n);wi为节点i上安装PMU时耗费的造价,在本文中将wi作为常数来处理。因此,可以将式(1)的数学模型简化为
(2)
式(2)中f(x)表示该电力系统配置PMU的最小数目。不失一般性,采用式(2)作为优化指标。
1.2 仅考虑系统全局可观测
对于一个具有n个节点的电力系统,系统全局可观测的约束条件可以表示为观测函数f(X),如下所示:
f(X)=AX≥M
(3)
式中:X=x1,x2,…,xnT;A是一个n×n的矩阵,表示电力系统的拓扑图所对应的邻接矩阵,如果节点i与节点j连通或者i=j,则aij=1,否则aij=0;M是一个n阶的单位列向量。
2.3.1 Box-Behnken模型建立及试验结果。通过响应面设计Box-Behnken对GASP提取率建立数学模型,优化提取工艺参数,共有17个试验点,12个分析因子,5个零点。以分析因子为自变量在A、B、C构成三维顶点;零点为区域的中心点。零点试验重复5 次,用以估算试验误差[20]。以GASP提取率为响应值,试验结果见表2。
以电力系统的IEEE-14节点系统[14]为例,如图1所示。图1中,横向粗实线表示节点,数字1~14表示14个节点的编号,细实线表示输电线,节点上的箭头表示该节点上有负载,G表示发电机,双圆圈符号表示变压器。
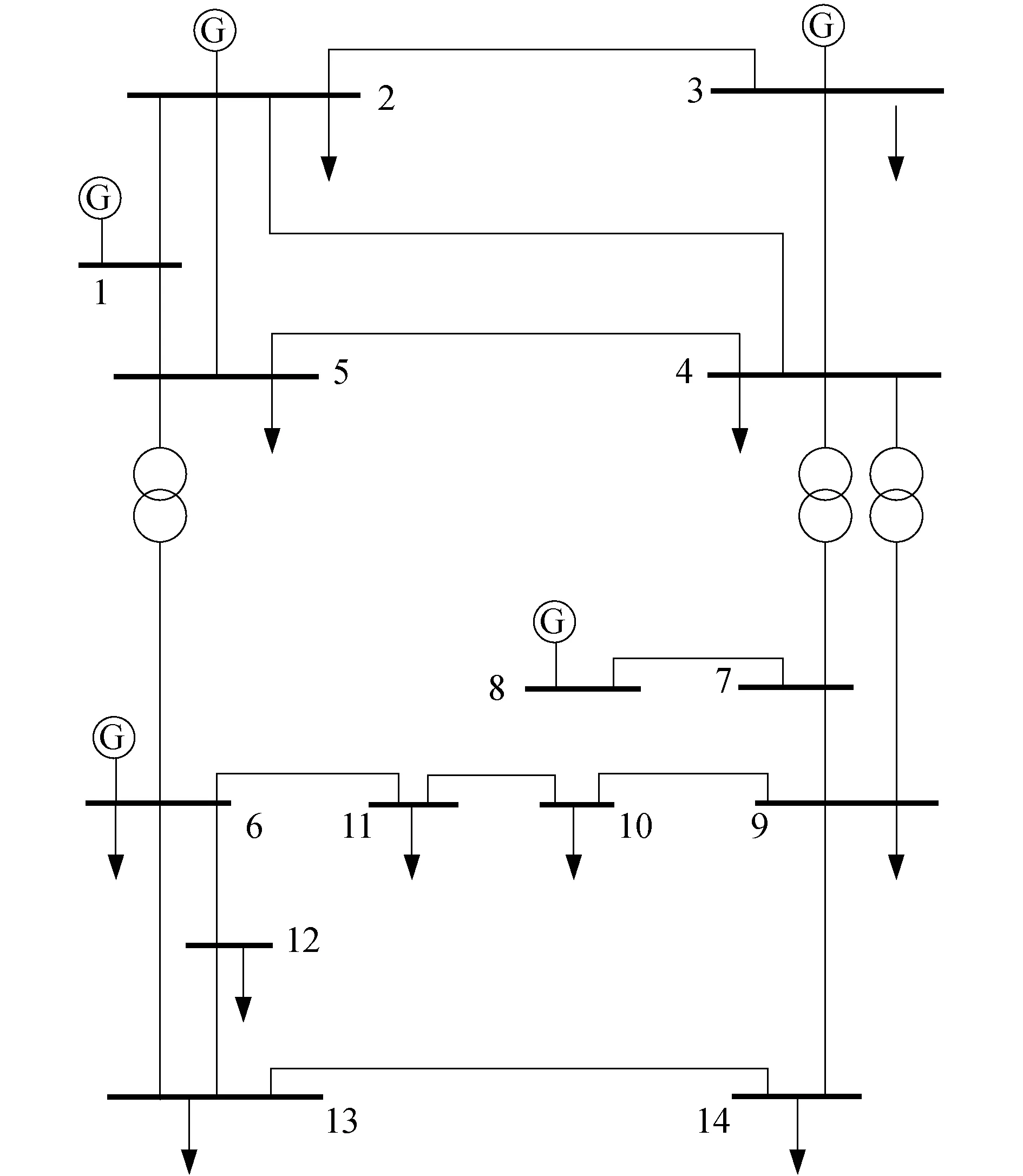
图1 IEEE-14节点系统拓扑结构Fig.1 Topology diagram of IEEE-14 bus system
由式(3)可知,对于节点1,为了达到节点1至少观测一次(f1≥1),那么必须在其相邻节点上配置PMU,即变量x1、x2或者x5中至少有一个值为非零。同理,如果整个IEEE-14节点系统完全可观测,fi≥1(i=1,2,…,14)就都要成立,即要求每一个fi表达式的变量都至少有一个非零。
此时,OPP问题的数学模型就为式(2)和式(3)的联立方程组。
1.3 考虑零注入节点且系统全局可观测
对于一个具有n个节点的电力系统,考虑零注入节点且要求系统全局可观测的约束条件可以表示为
f(X)=AX+C≥M′
(4)
同样以IEEE-14节点系统为例,讨论式(4)中零注入可观测向量C和修改后可观测需求向量M′的构成和取值。
在IEEE-14节点系统中,节点7为零注入节点,由图1可知,节点4、节点8和节点9与零注入节点7相连接。假设节点i为零注入节点,与节点i相连接的节点数为k,如果(k+1)个节点中有k个节点的电压可知,则可以计算出剩余那个节点的电压。因此,如果节点4、节点7、节点8和节点9中任意3个节点可观测,则通过计算可知第4个节点可观测。构造零注入可观测辅助变量h4、h7、h8、h9,如下所示:
(5)
式中:·表示逻辑与。比如,观测函数中的变量f7、f8和f9都非零时h4=1,否则h4=0。列向量C的定义如下所示:
(6)
列向量M′定义为[15]
(7)
在IEEE-14节点系统中,C和M′分别为
C=0,0,0,h4,0,0,h7,h8,h9,0,0,0,0,0T
(8)
M′=1,1,1,1,1,1,0,1,1,1,1,1,1,1T
(9)
此时,OPP问题的数学模型即为式(2)和式(4)的联立方程组。
2 PDE算法求解OPP问题的方法
本文提出的基于PDE算法求解OPP问题的具体流程如图2所示。图2中,P为种群迭代次数,Pmax为最大种群迭代次数。

图2 PDE算法求解OPP问题流程Fig.2 Flow chart of PDE for OPP problem
3 实验结果
本文按照第2节给出的PDE算法求解OPP问题流程,利用Matlab并行计算工具箱的spmd结构模块实现DE算法的并行化。在IEEE-14节点系统、IEEE-30节点系统和IEEE-57节点系统算例上进行差分进化和并行差分进化,分别考虑系统全局可观测和零注入节点且系统全局可观测2种场景,比较DE算法和PDE算法的寻优能力和收敛速度。
本实验环境如下所示:处理器为Intel(R) Core(TM) i3-3220 3.30 GHz;内存为4.00 GB RAM的操作系统,32 bit,Windows 7;Matlab版本为V7.11.0.584(R2010b)。
对同一系统,设置相同的算法参数,分别运用DE算法和PDE算法进行20次仿真实验。实验参数如表1所示。表1中,F为缩放因子,CR为交叉概率,D为数据的维数,N为个体的个数。Cmax定义为:假定某一个PMU配置候选解经过指定次数Cmax的迭代而保持不变,则认为算法已收敛,把该PMU配置候选解定义为PMU配置的最优解。仿真结果如表2和表3所示。

表1 DE算法和PDE算法初始参数设置Tab.1 Initial parameter setting of DE algorithm and PDE algorithm

表2 不考虑零注入节点情况下DE算法和PDE算法最优解对比Tab.2 Comparison of the best solution between DE algorithm and PDE algorithm without considering zero-injection node

表3 考虑零注入节点情况下 DE和PDE算法最优解对比Tab.3 Comparison of the best solution between DE algorithm and PDE algorithm considering zero-injection node
表2和表3是从PMU配置最优解平均值和在20次实验结果中得到最小PMU配置最优解次数2个方面对DE算法和PDE算法进行比较。从PMU配置最优解平均值可以看出,对于IEEE-14节点系统,PDE算法相对于DE算法的PMU配置最优解平均值基本相同。对于IEEE-30节点系统和IEEE-57节点系统,PDE算法的PMU配置最优解平均值优于DE算法。从得到最小PMU配置最优解次数可以看出,PDE算法在有限的运行次数中可以寻找到更优的OPP问题的解。因此,当节点系统的维数增大时,PDE算法的优势就会越明显。
4 结语
本文提出了一种全局可观测并行差分进化PMU配置方法。在不考虑零注入条件全局可观测PMU配置和考虑零注入条件全局可观测PMU配置2种情况下,将PDE算法与DE算法进行比较。结果表明,随着系统规模的提升,PDE算法获得比DE算法更优的PMU配置方案。
参考文献:
[1] KEKATOS V,GIANNAKIS G B,WOLLENBERG B.Optimal placement of phasor measurement units via convex relaxation[J].IEEE Transactions on Power Systems,2012,27(3):1521-1530.
[2] PENG C,XU X.A hybrid algorithm based on immune BPSO and N-1 principle for PMU multi-objective optimization placement[C]//International Conference on Electric Utility Deregulation and Restructuring and Power Technologies.[S.l.]:IEEE,2008:610-614.
[3] MILOSEVIC B,BEGOVIC M.Nondominated sorting genetic algorithm for optimal phasor measurement placement[J].IEEE Transactions on Power Systems,2003,18(1):69-75.
[4] AMINIFAR F,LUCAS C,KHODAEI A,et al.Optimal placement of phasor measurement units using immunity genetic algorithm[J].IEEE Transactions on Power Delivery,2009,24(3):1014-1020.
[5] SAJAN K S,TYAGI B.Optimal placement of PMU with optimal branch current phasors for complete and incomplete observability[C]//2011 IEEE Power and Energy Society General Meeting.[S.l.]:IEEE,2011:1-5.
[6] PENG J,SUN Y,WANG H F.Optimal PMU placement for full network observability using Tabu search algorithm[J].International Journal of Electrical Power and Energy Systems,2006,28(4):223-231.
[7] AMINIFAR F,KHODAEI A,FOTUHI-FIRUZABAD M,et al.Contingency-constrained PMU placement in power networks[J].IEEE Transactions on Power Systems,2010,25(1):516-523.
[8] GOU B.Optimal placement of PMUs by integer linear programming[J].IEEE Transactions on Power Systems,2008,23(3):1525-1526.
[9] DUA D,DAMBHARE S,GAJBHIYE R K,et al.Optimal multistage scheduling of PMU placement:an ILP approach[J].IEEE Transactions on Power Delivery,2008,23(4):1812-1820.
[10] STORN R,PRICE K.Differential evolution:a simple and efficient adaptive scheme for global optimization over continuous spaces[R].Berkley:International Computer Science Institute,1995.
[11] AI-MOHAMMED A H,ABIDO M A,MANSOUR M M.Optimal PMU placement for power system observability using differential evolution[C]//2011 11th International Conference on Intelligent Systems Design and Applications,Cordoba.[S.l.]:IEEE,2011:277-282.
[12] VENKATESWARAN V B,KALA V S C.Observability analysis and optimal placement of PMU using differential evolution algorithm[C]//2012 International Conference on Emerging Trends in Electrical Engineering and Energy Management.[S.l.]:IEEE,2012:205-209.
[13] VEDIK B,CHANDEL A K.Optimal placement of PMUs using differential evolution[C]//2013 International Conference on Intelligent Systems and Signal Processing.[S.l.]:IEEE,2013:17-22.
[14] CHRISTIE R.Power system test archive[DB/OL].[2018-01-05].http://www.ee.washington.edu/research/pstca.
[15] XU B,ABUR A.Optimal placement of phasor measurement units for state estimation[R].Texas:Texas A&M University,2005.

