波浪对级配砂海滩滩形塑造的试验研究❋

孙昶领， 郑建国， 许国辉❋❋, 朱旺平， 杨亚迪， 陶 威

(中国海洋大学 1.海洋环境与生态教育部重点实验室； 2.山东省海洋环境地质工程实验室，山东 青岛 266100)

海滩变化是海岸浪、潮、流等动力因子和海滩地形相互作用的结果，海滩剖面的形态是探究海滩变化的一个重要研究内容[1]。研究波浪作用下海滩剖面的响应规律，对于认识岸滩塑造规律和指导人工养滩等海岸防护工程具有重要的指导意义[2]。

自Cornaglia提出中立点理论以来，众多学者通过实测海滩剖面结合数学分析手段，提出了诸多平衡剖面形态模型。主要的剖面模型有Dean模型、Bodge模型、Lee模型[3-5]等。Shepard根据实际观测结果，给出了海岸前滩坡度与粒径的关系[6]，桥本和宇多通过观测结合试验资料得到了海滩坡度与泥沙中值粒径、平均波高的关系。Dean1973年提出了根据泥沙沉降一个波高距离用时与波周期的比值判定海滩剖面类型[7]，砂村和堀川进一步考虑原始岸滩坡度的影响，将海滩剖面分成了侵蚀型、过渡型、堆积型三类[2]。国内学者冯卫兵等通过室内水槽试验采用多个组合波对滩面进行作用，得到室内试验波浪间作用滩形的冲淤变化结果[8]。蒋昌波等通过室内水槽实验，用不同水深模拟海平面变化，探究由于海平面升降导致波浪动力因素变化情况下，海岸线和各种海岸地貌的响应规律、沉积物分选规律等，通过设置不同的初始坡度，探究坡度对于海滩剖面的影响规律[9-10]。数值模拟方面，张弛等通过数值模拟，建立了波浪、底部离岸流、泥沙运动和沙滩剖面演变耦合数学模型，讨论了各个物理参数对剖面上的水动力和地形变化的影响[11]。李志强等将实际沙滩与已有模型进行结合讨论，分析各参数物理意义，探讨各模型参数之间的关系[12]。

海滩剖面在不同动力作用下是变化的，其变化内在要素受控于海滩泥沙粒径，外部受控于动力大小。已有研究海滩剖面形态工作，主要考虑了海滩砂粒径和波浪强度的影响，而尚缺乏对级配砂海滩滩形的研究。本文通过波浪水槽试验，用不同粒径和级配的砂，铺设成初始地形完全相同的海滩，施加不同的波浪作用，研究海滩剖面的变化。

1 试验概况

1.1 试验材料与装置

试验用沙取自青岛市天然沙滩，用标准孔目的孔筛进行筛分，获得粗砂(0.5～2 mm)、中砂(0.25～0.5 mm)、细砂(0.125～0.25 mm)等3种单一粒组的试验用砂。级配砂用获得的粗砂、中砂、细砂按照一定比例混合获得。试验沙床的沙级配曲线如图1，其中值粒径见表1。

试验设备主要为波浪水槽。该水槽长14 m，宽0.5 m，高0.7 m，配有造波系统，可形成规则波。水槽上设有超声地形自动测量分析系统，可精确测量地形(毫米级)。试验中使用了DEWE43V数据采集系统(误差小于0.1 mm)、波高仪(误差小于1 mm)、DV录像机等测量仪器(见图2a)。在铺设的沙滩段，水槽中间设置了沿波浪传播方向的隔离钢板，钢板两侧形成独立的试验区间A、B，同时进行不同粒径或级配泥沙的试验(见图2b)。

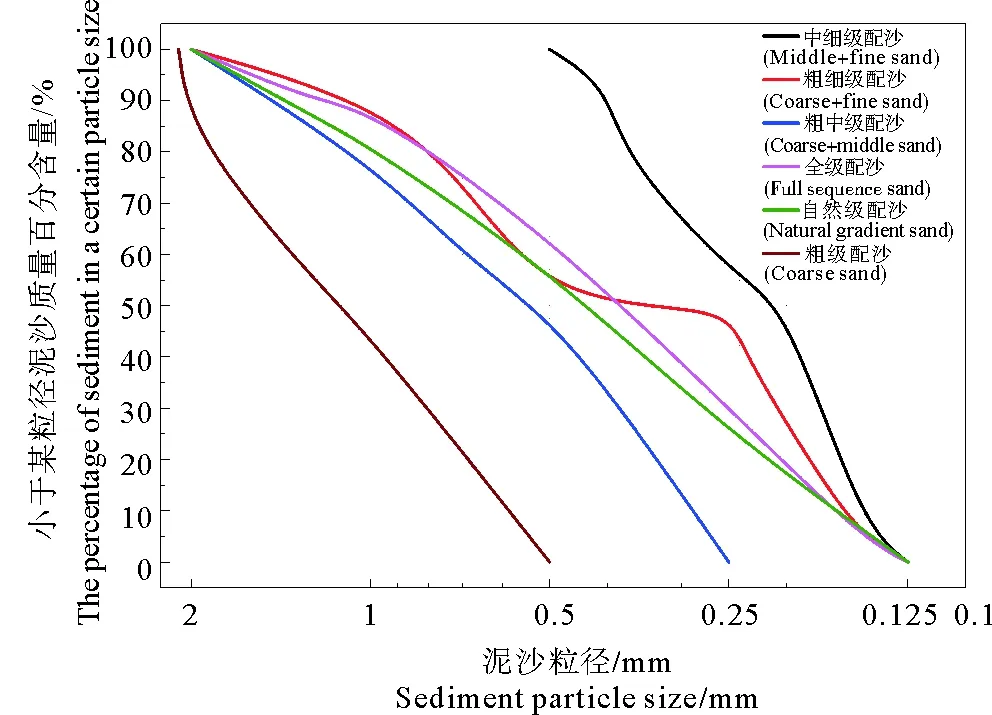
图1 试验沙床沙级配曲线Fig.1 Grain-size distribution of sand used in this experiment

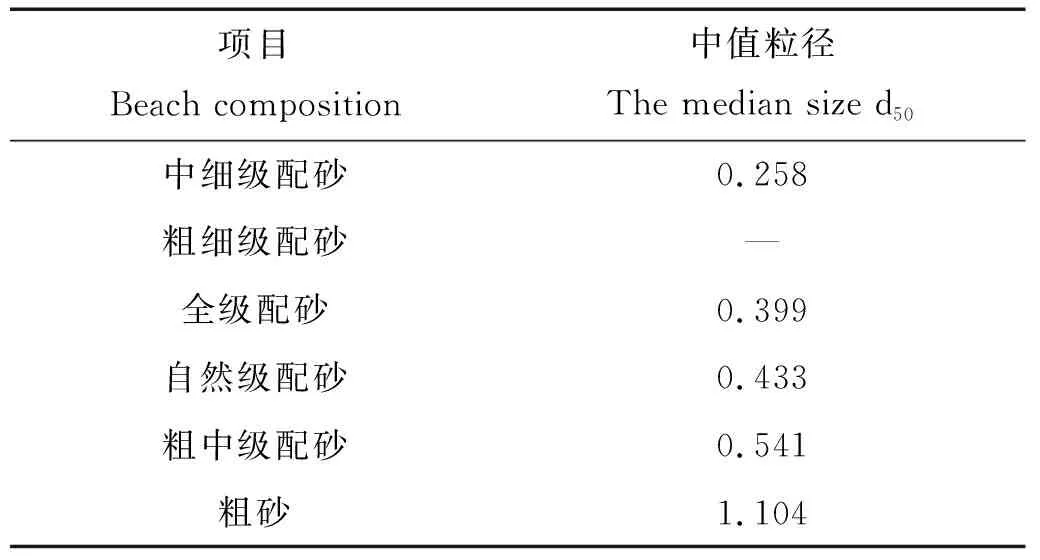
项目Beach composition中值粒径 The median size d50中细级配砂0.258粗细级配砂—全级配砂0.399自然级配砂0.433粗中级配砂0.541粗砂1.104

1.2 试验波况与程序

对水槽中铺设的沙滩，设计了不同波周期和波高的波浪作用(见表2)。试验水深均设置为0.35 m。初始滩形采用组合坡度，下部为1∶7，上部为1∶15(见图2a)。试验过程中，首先在水槽的A区和B区分别铺设试验用沙；铺设完毕将水位加至0.6 m，没过整个试验滩面并浸泡12 h，随后用超声地形自动测量分析系统记录沙滩原始面；测量结束后放水至0.35 m水深，造波试验；观察并记录试验现象，记录剖面滩肩沙坝的位置以及移动状态，待滩面稳定后停波(一般在波浪作用30 min以内滩面地形即达到稳定)；将水槽水位调至地形分析系统工作水位，测量沙滩稳定剖面地形；测量结束后将沙滩充分掀起，搅拌均匀，并将滩形恢复至初始状态，重复上述过程。待该组沙所有波况试验完毕后，换沙进行重复试验。

(图a为水槽正视图:Front elevation；图b为水槽俯视图:Top view)图2 试验布置示意图Fig.2 Experimental setup

序号Serial number沙滩组成Beach composition波高Wave height H=12.5 cmT=1.0 sT=1.4 sT=1.8 s周期Wave Period T=1.68 sH=6.7 cmH=8.6 cmH=13.2 cm1粗砂√√√√√2粗+中√√√√√3粗+细√√√√√4中砂√√√√√5中+细√√√√√6细砂√√√√√7全级配√√√√√8自然砂√√√√√

注:混合沙床按照等质量比混合，如“粗+中”，即为粗、中沙质量各占50%。

Note: Sand beds are mixed by percent of mass. The “coarse+middle” sand means coarse sand and middle sand each half.

2 试验结果与分析

将各粒径和级配的泥沙组成的沙滩，在不同波浪作用下形成的地形绘制成图(见图3)。图3a、3b、3c分别是控制相同波高H=12.5 cm，周期分别是1.0、1.4、1.8 s波况条件下作用的滩形。图3d是波高H=6.7 cm，周期为1.68 s波况作用下的滩形。试验沙滩地形数据给出了水下沙坝和滩肩与水位线的相对位置关系。根据砂村和堀川依据泥沙堆积位置的滩形分类标准，图3中a、b、c所给出的地形均为侵蚀型和过渡型。对同一滩面，施以不同波况作用，水下沙坝的位置会稍有不同，当施以长周期、低波高的波浪作用时，沙滩易形成滩肩型剖面，当施以中短周期波或长周期大波高的波浪作用时，易形成沙坝型剖面。

2.1 分析用参数的定义

为了便于分析不同波浪作用下不同粒径和级配的沙滩滩形特征，本文选择中砂粒组作为参照组，提出了相对坡度、相对位置、相对高度等概念。

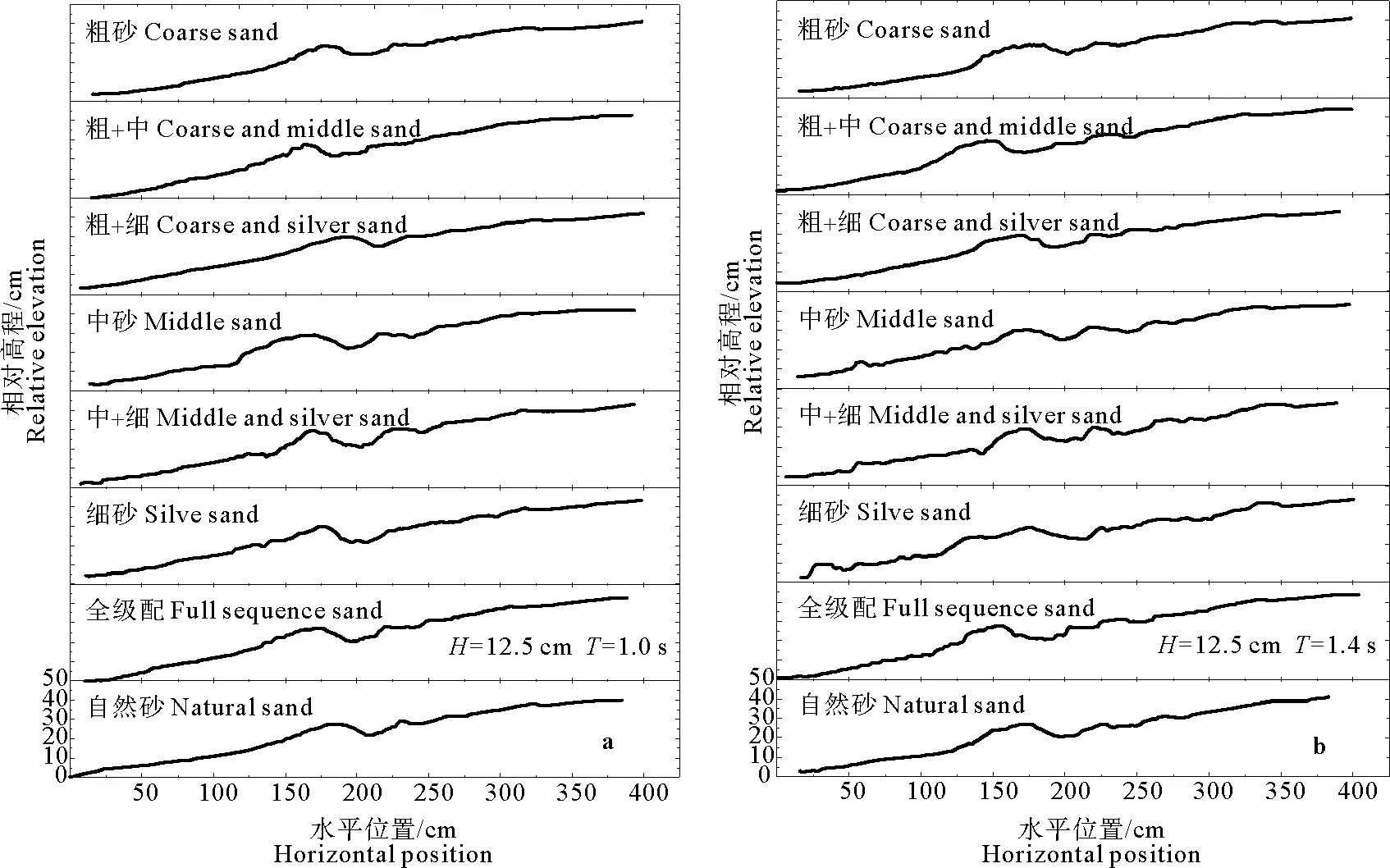
(图a、b、c波浪条件：波高H=12.5 cm，波周期分别为1.0 s，1.4 s，1.8 s，图d波浪条件：波高H=6.7 cm，周期T=1.68 s。Diagram abc:wave heightH=12.5 cm,wave period:1.0 s,1.4 s,1.8 s, diagram d:wave heightH=6.7 cm, wave periodT=1.68 s.)

图3 沙滩波浪水槽试验滩形剖面
Fig.3 Beach profile

2.1.1 相对坡度 相对坡度：指在波浪作用后某一试验沙滩的稳定坡度与中砂粒组沙滩稳定坡度的比值。又划分为全滩相对坡度、沙坝前和沙坝后相对坡度。全滩是指自试验底床水下斜坡起点到滩肩，沙坝前是指沙坝迎浪面到坝顶，沙坝后是指坝顶到坝后凹槽。根据试验沙滩地形数据计算获得全滩、沙坝前后的坡度值(见表3)，与中砂沙滩坡度数据进行比较后，给出全滩、沙坝前后的相对坡度值(见表4)。

表3 沙床稳定坡度值Table 3 The stable value of the gradient of sand bed

2.1.2 相对位置 相对位置：指在波浪作用后某一试验沙滩的稳定特征形态位置与中砂粒组沙滩稳定特征形态位置的比值。划分为沙坝相对位置和滩肩相对位置。沙坝位置用坝顶位置标示，滩肩位置用滩肩顶位置标示。利用试验沙滩地形数据给出滩肩和沙坝的位置，以中砂沙滩的滩肩和沙坝位置作为参考后，给出滩肩和沙坝的相对位置(见表5)。

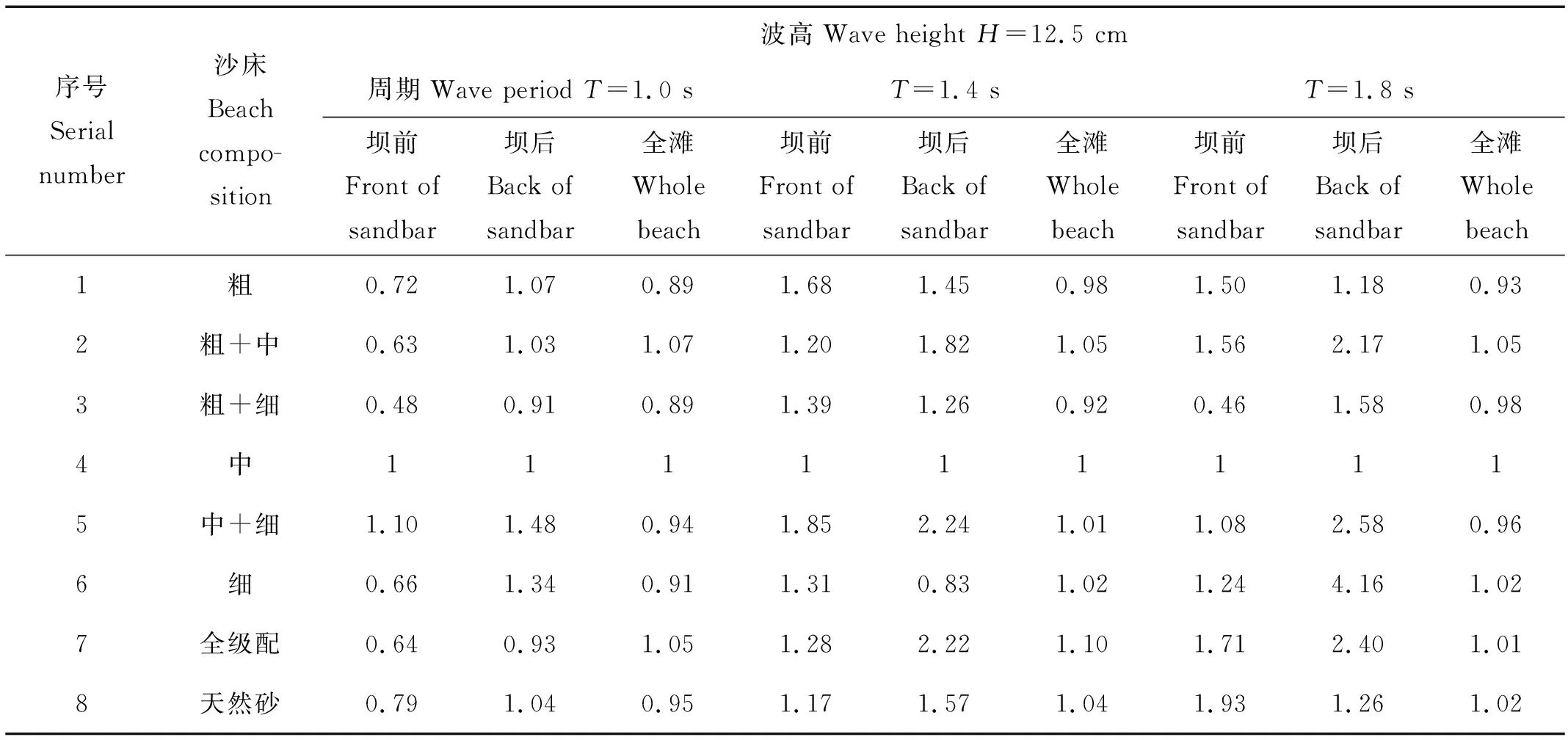
表4 沙床相对坡度值Table 4 The relative value of gradient of sand bed

表5 剖面滩肩、沙坝的位置和相对位置Table 5 The relative position of sand bar and beach berm

注:表中位置数值为特征地形相对于沙滩坡底的水平距离，单位cm。

Note: The number of position is the horizontal distance between representative terrain and beach bottom. Unit: centimeter.

2.1.3 相对高度 相对高度：指在波浪作用后某一试验沙滩的稳定沙坝高度与中砂粒组沙滩稳定沙坝高度的比值。表6给出了不同波况下沙坝型剖面坝高与相对高度值。

表6 沙坝型剖面坝高与相对高度Table 6 Sandbar height and relative height of bar type profile

2.2 滩形变化与沙滩粒径及级配关系分析

2.2.1 沙床稳定坡度对比 表3和表4分别给出了在室内水槽试验条件下，沙床沙坝坡度、滩肩坡度、全滩坡度以及相对坡度值。

由表可知，当沙床在相对较小的波周期T=1.0 s波浪作用下，粗细混合沙床滩面坡度最小，中细混合沙床的坝前和坝后坡度最大。沙床在波周期T=1.4 s、T=1.8 s波况作用时，纯粒径沙床坝前坡度与全滩坡度大小关系一致：坝前坡度粗砂最大，细砂次之，中砂最小；全滩坡度细砂最大，中砂次之，粗砂最小。在波高为12.5 cm，波周期分别为1.0 s、1.4 s、1.8 s作用时，粗中混合沙床与全级配沙床的全滩坡度均大于其余沙床。

天然沙、全级配沙床以及粗中砂混合沙床在室内水槽条件下，当波高相同时，坝前坡度随波周期的增大而增大。级配砂沙床，将粗砂与粗细混合砂、中砂与中细混合砂、粗中混合砂与全级配沙床坡度两两对比可知，在混合沙床各粒径泥沙同时存在时，对沙床坡度起决定性影响的为粗颗粒泥沙。

2.2.2 沙坝与滩肩的相对位置对比 图4给出了不同粒径泥沙滩面在周期相同(T=1.68 s)，施以不同波高波况作用下海滩剖面对比情况。由图可知，当周期相同，波高越高，海滩越容易形成沙坝型剖面，波高越低，越容易形成滩肩型剖面。即当周期相同时，波高越高，波能越大，对沙滩的冲击作用更为明显，海滩更容易被侵蚀；波高越低，相对波能较小，海滩更容易淤积。

图5给出了相同波高(H=12.5 cm)不同周期(T=1.0 s，1.4 s，1.8 s)波况下，形成的稳定的海滩剖面。其中，图a为粗细砂混合沙滩，图b天然砂沙滩。根据实验结果可知，波高相同周期不同的波浪作用下，海滩剖面均为水下沙坝型。结合图5和表5看出，整个沙滩坡脚较为平整，无明显起伏变化。水下沙坝在波周期T=1.4 s的波况作用后，滩形整体更趋向于海，在波周期T=1.8 s的波浪作用下形成的滩面整体更趋向于岸。相对长周期波况下形成的滩后淤积量远超于中短周期波，滩肩高度高于中短周期波。

在对比剖面水下沙坝相对位置时，既要考虑波浪动力的影响，也要考虑沙床粒径的影响。图6给出了粗砂、中砂和细砂滩面在不同波况作用下的滩形对比图，其中图a,b,c分别为波高H=12.5 cm、波周期为1.0 s、1.4 s、1.8 s的条件，图d为波高H=6.7 cm、波周期T=1.68 s的情况。

粗、中、细粒径滩面在同种波况作用下滩形变化规律不同。由表5可知，在纯粒径沙床中，粗砂沙床沙坝位置最为靠岸，中砂沙床和细砂沙床沙坝位置更为向岸，在相对短周期波(T=1.0 s)波况作用下，粗砂沙床与细砂沙床的滩肩与沙坝的相对位置变化规律相同。由图6a可知，在短周期波作用下，中砂沙滩剖面沙坝宽度更大，形成的滩后淤积滩肩长度更长，且三条滩形剖面线与水深线交于一点。由图6b可知，当波周期为1.4 s时，细砂滩面形成的沙坝最宽，中砂沙坝高度略高于另外两组，三种沙滩剖面，由岸至海分别为粗、中、细，即细颗粒在波浪作用下向海发生的横向输移更为明显。由图6c可知，当波周期为1.8 s时，三种滩形均为沙坝与滩肩过渡型剖面，其中，粗砂沙坝高度最低，中砂最高，细砂沙坝移动位置更为靠海，粗砂靠岸，中砂介于两者之间。粗砂滩后淤积量最小，滩肩位置更为靠海。细砂滩后淤积量最大，滩肩高度最高，宽度最大，中砂滩面介于二者之间。在1.4 s，1.8 s波周期作用下，细砂与粗砂滩前均出现规则沙纹，沙床靠海位置呈现规律的锯齿状(见图7)。由图6d可知，在相对长周期小波高(T=1.68 s，H=6.7 cm)的波况作用下，滩形剖面为滩肩型，即向岸淤积型，由海至岸向分别是粗砂、中砂、细砂滩面，细砂淤积量最大，粗砂最小，中砂介于二者之间。

(沙床类型：a为粗砂+中砂，b粗砂+细砂，c粗砂，d天然砂。The type of sand bed: a:coarse sand+middle sand, b:coarse sand+silver sand，c：coarse sand, d:natural sand.)

图4 相同周期不同波高作用下滩形对照图
Fig.4 The beach profile under the action of different wave height in the same wave period

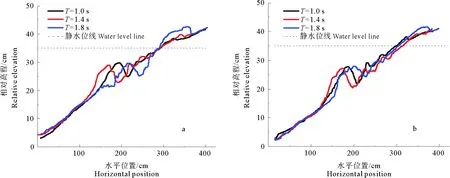
(沙床类型：a为粗砂+细砂，b天然砂。The type of sand bed: a: coarse sand+ silver sand, b: natural sand.)

(图abc波高H=12.5 cm，波周期分别为1.0 s，1.4 s，1.8 s，图d波高H=6.7 cm，周期T=1.68 s。Diagram abc: wave heightH=12.5 cm, wave period: 1.0 s, 1.4 s, 1.8 s, diagram d: wave heightH=6.7 cm, wave periodT=1.68 s.)

图6 单一粒径沙床海滩剖面对比示意图
Fig.6 Single particle size of sand bed beach profile contrast diagram

图7 局部沙纹示意图Fig.7 Partial diagram of sand wave

由于沙坝移动方向与沙坝坝顶净输沙方向一致[13-14]，因此，可以用沿岸输沙规律来解释沙坝的运动规律。影响沿岸输沙的主要因素，内部来自于泥沙粒径，外部受制于波浪动力条件。图8给出了部分波高仪数据记录，由图可知，两侧沙床波浪从波峰至波谷所用时间均大于波谷至波峰时间，因此，在试验过程中，滩形变化一直受波浪的非线性的影响。在室内水槽试验条下，影响输沙的主要因素为泥沙自重、海底回流强度、波浪的非线性作用。其中，海底回流使得泥沙发生离岸运动，波浪的非线性作用使得泥沙向岸运动[15-16]，泥沙运动的最终趋势取决于上述三个因素的相对大小。

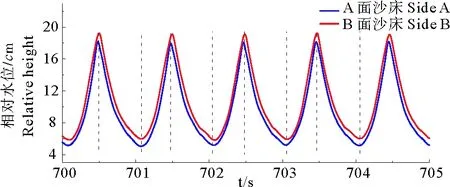
图8 波高仪波形记录图Fig.8 Wave probe image

海底回流强度会随波高的增大而增大，当波高增大，海底回流强度增大，但波浪的非线性作用并不能继续增大，故海底回流强度的大小成为大波高波况下沙坝运动的主导因素，沙坝离岸运动；当波高较小，回流强度弱，非线性作用相对较强，此时沙坝发生向岸运动，这也解释了图6c、6d两图滩形的不同。单一粒径沙质滩面，在不与其他粒径进行混合的情况下，沙床的孔隙随着粒径的增加而增大，即，在粗、中、细砂沙床中，粗砂沙床孔隙最大，细砂沙床孔隙最小。波浪在滩面上破碎，波能会在滩面上发生反射，当波浪在粗颗粒滩面上破碎，由于孔隙大，波能耗散更为彻底，泥沙向岸、向海运动量较小，因此，滩面粒径越粗，在波浪作用后的滩形更为平整。

2.2.3 水下沙坝特征 表6给出了在相同波高下，对不同滩面施以不同周期波浪作用后，水下沙坝的高度值与相对高度值。由表可知，在级配沙沙床中，中细砂混合沙床和粗细砂混合沙床在各个波况下形成的沙坝高度均大于其他级配砂沙床，在纯粒径沙床中，中砂沙床在相对中长周期波况作用时，沙坝高度值较大，细砂沙床沙坝高度随波周期的增大而减小。

将同一滩面在不同波况作用下的滩形进行对比可知，在室内水槽波浪条件下，沙滩在中长周期波况作用时，影响水下沙坝高度的主要因素为泥沙粒径；当波周期较短时，粒径的影响因素较小，各个剖面滩形相似且形成的水下沙坝高度趋于一致。

已有研究给出水下沙坝的形状与波浪大小无关，沙坝深槽的水深ht与坝顶水深hc之比即奎利根比是一定值1.69。本文整理了各组试验获得的水下沙坝的奎利根比(见表7)。将试验获得的奎利根比与1.69做了相对误差分析(试验的奎利根比与1.69差值的绝对值除以1.69)，发现试验获得的水下沙坝的奎利根比并非定值，试验沙床的粒径和级配对奎利根比有影响。

由表7可知，在相对短周期波况(T=1.0 s)作用下，奎利根比随沙床平均粒径的增大而逐渐减小。由图5可知，当沙床在相对长周期波(T=1.8 s)波况作用下，滩形整体更趋向于岸。在波高一定时，波周期越长，越容易形成滩肩型剖面，因而整体坡面与沙坝处相对较为平缓，沙坝坝高与坝后凹槽高度差值较小，奎利根比随之减小。结合图5和表7可知，当波周期在1.8 s时，中砂沙床形成了双沙坝地形，其沙坝坝高与坝后槽深相对高度差值较小，故中砂沙床奎利根比值在该波况下变化趋势与相对中短周期波况有所不同。天然沙与全级配沙床在中短周期波浪作用下，沙坝位置有差异，但相对高度差值较小，奎利根比值趋于一致。结合图5、表6、表7可知，沙床在波高一定时，沙坝坝后凹槽相对深度随波周期的增大而减小，但沙坝坝高并没有显著变化，因此奎利根比随之减小。在水槽试验条件下，奎利根比值的相对大小可用来描述沙坝型剖面的沙坝处地形特点。

表7 沙床试验的水下沙坝奎利根比ht/hc与相对误差值Table 7 The Keulegan number of sand bed ht/hc and relative value

3 结论

本文在水深和沙床坡度统一的情况下，通过改变波周期、波高等波浪要素来概化波浪动力条件的改变，研究不同泥沙粒径沙床剖面形态的变化，主要结论如下：

(1)在室内水槽波浪条件下，当波高相同时，波周期越大，坝前坡度越大；当波周期相同，波高越高，坝前坡度越大，试验形成的沙坝型剖面的坝前坡度主要受制于波浪动力条件。在混合级配沙床中，对沙床坡度起决定性影响的为粗颗粒泥沙。当波高相同，相对长周期波作用下形成的滩面整体更趋向于岸，滩后淤积量大，滩肩高度更高。

(2)当波周期相同，波高越高，海滩越容易形成沙坝型剖面，波高越低，越容易形成滩肩型剖面。换言之，在同周期波况下，波高越高，波能越大，对沙滩的冲击作用更为明显，海滩更容易被侵蚀。当波周期相同时，沙床粒径越细，形成水下沙坝沙坝宽度越大，沙坝位置更为向海，滩肩更长且相对位置更为向岸。

(3)试验条件下，当周期较长时，影响水下沙坝高度的主要因素为泥沙粒径；当波周期较短时，粒径的影响较小，各个滩面剖面滩形相似且形成的水下沙坝高度基本一致。细砂沙床形成的沙坝高度随波周期的增大而减小。粒径越细，横向输移量越大。

(4)室内试验获得的沙坝型剖面奎利根比并非定值，该比值与沙床粒径以及波况有关。当波高固定时，奎利根比值随波周期的增大而减小；当波况固定时，奎利根比值随沙床平均粒径的增大而减小。

参考文献：

[1] 邹志利. 海岸动力学[M]. 北京: 人民交通出版社， 2009.

ZOU Zhi-Li. Coastal Hydrodynamics[M]. Beijing: China Communications Press, 2009.

[2] 严恺. 海岸工程[M]. 北京： 北京海洋出版社， 2002.

YAN Kai. Coastal Engineering [M]. Beijing: Beijing Ocean Press, 2002.

[3] Dean R G. Equilibrium Beach profiles: characteristic sand applications [J]. Journal of Coastal Research, 1991, 7(1): 53-84.

[4] Bodge K R. Representing equilibrium beach profiles with an exponential expression [J]. Journal of Coastal Research, 1992, 8(1): 47-55.

[5] Lee Z F. The submarine equilibrium profile: a physical model [J]. Journal of Coastal Research, 1994, 10(1): 1-17.

[6] Shepard F P, Curray J R, Inman D L, et al. Submarine geology by diving saucer [J]. Science, 1964, 145(3636): 1042-1046.

[7] Dally W R, Dean R G, Dalrymple R A. Wave height variation across beaches of arbitrary profile [J]. Journal of Geophysical Research Atmospheres, 1985, 90(NC6): 11917-11927.

[8] 冯卫兵, 李冰, 王铮,等. 二维沙质海滩剖面形态试验研究[J]. 海洋通报, 2008, 27(5): 110-115.

FENG Wei-Bing, LI Bing, WANG Zheng. Experimental study on the profile shapes of sandy beach [J]. Marine Science Bulletin, 2008, 27(5): 110-115.

[9] 蒋昌波, 陈杰, 程永舟,等. 海啸波作用下泥沙运动——Ⅰ. 岸滩剖面变化分析[J]. 水科学进展, 2012, 23(5): 665-672.

JIANG Chang-Bo, CHEN Jie, CHENG Yong-Zhou. Study of sediment transport by tsunami waves: Ⅰ: Beach profile evolution [J]. Advances in Water Science, 2012,23(5): 665-672.

[10] 蒋昌波, 伍志元, 陈杰,等. 波浪动力因素变化对沙质岸滩演变的影响[J]. 海洋学报, 2015, 37(3): 106-113.

JIANG Chang-Bo， WU Zhi-Yuan, CHEN Jie. Effects of wave dynamic factors on the evolution of sandy beach [J]. Acta Oceanologica Sinica, 2015, 37(3): 106-113.

[11] 张弛, 郑金海, 王义刚. 波浪作用下沙坝剖面形成过程的数值模拟[J]. 水科学进展， 2012, 23(1): 104-109.

ZHANG Chi, ZHENG Jin-Hai, WANG Yi-Gang. Numerical simulation of wave-induced sandbar formation[J]. Advances in Water science, 2012, 23(1): 104-109.

[12] 李志强, 陈子燊. 海滩平衡剖面模型中参数意义及相互关系探讨[J]. 海洋工程, 2009, 27(4): 108-115.

LI Zhi-Qiang, CHEN Zi-Shen. Analysis on the parameters’ meanings and relations in equilibrium beach profile models [J]. The Ocean Endineering, 2009, 27(4): 108-115.

[13] 张洋, 邹志利, 苟大荀,等. 海岸沙坝剖面和滩肩剖面特征研究[J]. 海洋学报, 2015, 37(1): 147-157.

ZHANG Yang, ZOU Zhi-Li, GOU Da-Xun. Experiment study on the evolution and geometrical characteristics of sandbar profile and berm profile [J]. Acta Oceanologica Sinica, 2015,37(3): 106-113.

[14] 尹晶, 邹志利, 李松. 波浪作用下沙坝不稳定性实验研究[J]. 海洋工程, 2008, 26(1): 40-50.

YIN Jing, ZOU Zhi-Li, LI Song. Unstable sandbar movement under wave action [J]. China Ocean Engineering, 2008, 26(1): 40-50.

[15] Aubrey D G. Seasonal patterns of onshore/offshore sediment movement [J]. Journal of Geophysical Research Oceans, 1979, 84(C10): 6347-6354.

[16] Sunamura T. Quantitative predictions of beach-face slopes [J]. Geological Society of America Bulletin, 1984, 95(2): 370-376.

[17] Larson M, Kraus N C, Wise R A. Equilibrium beach profiles under breaking and non-breaking waves [J]. Coastal Engineering, 1999, 36(1): 59-85.